2 Differentiation 2 1 2 2 2 3

Скачать презентацию 2 Differentiation 2 1 2 2 2 3

c0d4a4534a2385b90954cfb43a55bce8.ppt

Количество слайдов: 93

2. 1 The Derivative and the Tangent Line Problem Objectives n Find the slope of the tangent line to a curve at a point. n Use the limit definition to find the derivative of a function. n Understand the relationship between differentiability and continuity. Copyright © Cengage Learning. All rights reserved.

The Tangent Line Problem Calculus grew out of four major problems that European mathematicians were working on during the seventeenth century. 1. The tangent line problem 2. The velocity and acceleration problem 3. The minimum and maximum problem 4. The area problem Each problem involves the notion of a limit, and calculus can be introduced with any of the four problems. 3

Definition of the Derivative of a Function (x+Δx, f(x+Δx)) (x, f(x)) 4

The Derivative of a Function The most common notations that are used to denote the derivative of y = f(x) are The notation dy/dx is read as “the derivative of y with respect to x” or simply “dy, dx. ” Using limit notation, you can write 5

Example 1 – The Slope of the Graph of a Linear Function Find the slope of the graph of f(x) = 2 x – 3 at the point (2, 1). To find the slope of the graph of f at any given value for x use the definition of the derivative 6

Example 3 – Finding the Derivative by the Limit Process Find the derivative of f(x) = x 3 + 2 x. = 3 x 2 + 2 7

Example 4 – Finding the Derivative by the Limit Process Given Find Then find the slopes of the graph f at the points (1, 1) and (4, 2). Discuss the end behavior of f at (0, 0). Slope at (1, 1) is ½ Slope at (4, 2) is ¼ Discuss the end behavior of f at (0, 0). The slope at (0, 0) doesn’t exist since the 8 slope from the right and left at (0, 0) for the original function isn’t the same value.

Example 5 – Finding the Derivative by the Limit Process Find the derivative of y with respect to t for the function y = 2/t. 9

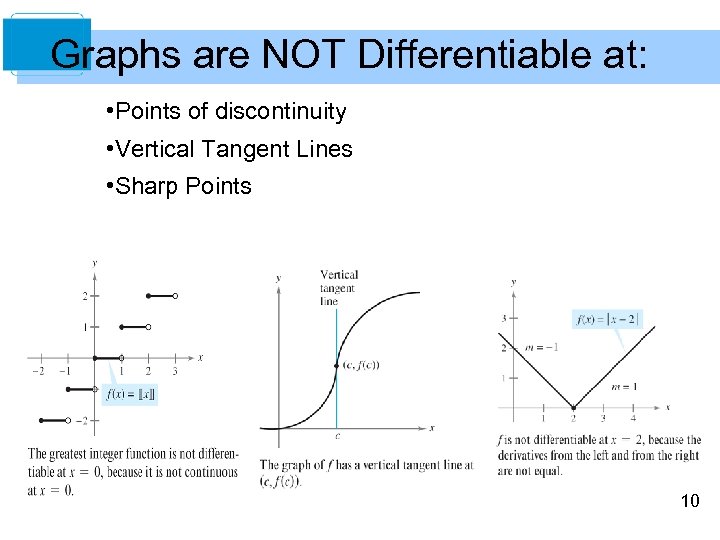Graphs are NOT Differentiable at: • Points of discontinuity • Vertical Tangent Lines • Sharp Points 10

2. 1 Summary Objectives n Find the slope of the tangent line to a curve at a point. n Use the limit definition to find the derivative of a function. n Understand the relationship between differentiability and continuity. Copyright © Cengage Learning. All rights reserved. 11

2. 2 Basic Differentiation Rules and Rates of Change Objectives n Find the derivative of a function using the Constant Rule. n Find the derivative of a function using the Power Rule. n Find the derivative of a function using the Constant Multiple Rule. n Find the derivative of a function using the Sum and Difference Rules. n Find the derivatives of the sine function and of the cosine function. n Use derivatives to find rates of change. Copyright © Cengage Learning. All rights reserved. 12

The Constant Rule Given function f(x) = c find the derivative 13 Figure 2. 14

The Power Rule Yesterday we found derivatives of functions like the following using the definition of the derivative. Please look for a pattern, rule, shortcut, …. for the following derivative f(x) = x 3 f'(x) = 3 x 2 f(x) = x 1/2 f'(x) = ½ x– 1/2 y = x 10 dy/ dx = 10 x y = x– 2 y' = – 2 x– 3 9 14

Example 1 – Finding the Derivative f(x) = x 7 y = x– 3 f'(x) = 7 x 6 dy/ dx = – 3 x – 4 f(x) = x 5/2 f'(x) = 5/2 x 3/2 y = x y' = 1 x 0 = 1 f(x) = 6 f'(x) = 0 15

Example 2 – Using the Power Rule Re-write Differentiate Simplify 16

The Constant Multiple Rule and the Power Rule can be combined into one rule. The combination rule is 17

Example 3 – Using the Constant Multiple Rule 18

Ex 4 – Find the Slope of a Graph Find the slope of the graph of f(x) = x 4 when a) x = -1 b) x = 0 c) x = 1 The slope is found by evaluating the derivative at the given values What is the derivative of f(x) = f′(x) = 4 x 3 a) The slope at x = -1 f’(-1) = 4(-1)3 = -4 b) The slope at x = 0 f’(0) = 4(0)3 = 0 c) The slope at x = 1 f’(1) = 4(1)3 = 4 19

Ex 5 – Find the Equation of a Tangent Line Find the equation of the tangent line to the graph of f(x) = x 2 when x = -2 We will use the point-slope formula after finding the point and the slope for the tangent line The Point: (-2, f(-2)) (-2, 4) The Slope: m = f′(-2) f′ (x) = 2 x f′ (-2) = -4 m = -4 Find the equation of the line passing through (-2, 4) with a slope of -4 y – 4 = – 4(x + 2) y = – 4 x – 4 20

The Sum and Difference Rules Example 6: 21

Proof of the Derivative of Sinx Find the Derivative of sinx using the definition of the Derivative Reminder from Ch 1 Reminder from section 2. 1 = cosx Extra Credit for proving 22 derivatives of all six trig functions

Derivatives of the Sine and Cosine Functions Example 7: 23

Rates of Change You have seen how the derivative is used to determine slope. The derivative can also be used to determine the rate of change of one variable with respect to another. Applications involving rates of change occur in a wide variety of fields. A few examples are population growth rates, production rates, water flow rates, velocity, and acceleration. 24

Rates of Change A common use for rate of change is to describe the motion of an object moving in a straight line. In such problems, it is customary to use either a horizontal or a vertical line with a designated origin to represent the line of motion. On such lines, movement to the right (or upward) is considered to be in the positive direction, and movement to the left (or downward) is considered to be in the negative direction. 25

Rates of Change The function s that gives the position (relative to the origin) of an object as a function of time t is called a position function. If, over a period of time t, the object changes its position by the amount s = s(t + t) – s(t), then, by the familiar formula the average velocity is 26

Example 9 A – Finding Average Velocity of a Falling Object If a billiard ball is dropped from a height of 100 feet, its height s at time t is given by the position function s = – 16 t 2 + 100 Position function where s is measured in feet and t is measured in seconds. Find the average velocity over the time interval [1, 2]. For the interval [1, 2], the object falls from a height of s(1) = – 16(1)2 + 100 = 84 feet to a height of s(2) = – 16(2)2 + 100 = 36 feet. The average velocity is 27

Example 9(b) – cont’d If a billiard ball is dropped from a height of 100 feet, its height s at time t is given by the position function s = – 16 t 2 + 100 Position function where s is measured in feet and t is measured in seconds. Find the average velocity over the time interval [1, 1. 5]. For the interval [1, 1. 5], the object falls from a height of 84 feet to a height of 64 feet. The average velocity is Note that the average velocities are negative, indicating that the object is moving downward. 28

Rates of Change In general, if s = s(t) is the position function for an object moving along a straight line, the velocity of the object at time t is In other words, the velocity function is the derivative of the position function. Velocity can be negative, zero, or positive. The speed of an object is the absolute value of its velocity. Speed cannot be negative. 29

Rates of Change The position of a free-falling object (neglecting air resistance) under the influence of gravity can be represented by the equation where s 0 is the initial height of the object, v 0 is the initial velocity of the object, and g is the acceleration due to gravity. On Earth, the value of g is approximately – 32 feet per second or – 9. 8 meters per second. 30

Example 10 – Using the Derivative to Find Velocity At time t = 0, a diver jumps from a platform diving board that is 32 feet above the water (see Figure 2. 21). The position of the diver is given by s(t) = – 16 t 2 + 16 t + 32 Position function where s is measured in feet and t is measured in seconds. a. When does the diver hit the water? b. What is the diver’s velocity at impact? Figure 2. 21 31

Example 10(a) – Solution a. When does the diver hit the water? s(t) = – 16 t 2 + 16 t + 32 Position function To find the time t when the diver hits the water, let s = 0 and solve for t. – 16 t 2 + 16 t + 32 = 0 – 16(t + 1)(t – 2) = 0 t = – 1 or 2 Set position function equal to 0. Factor. Solve for t. Because t ≥ 0, choose the positive value to conclude that the diver hits the water at t = 2 seconds. 32

Example 10(b) – Solution cont’d b. What is the diver’s velocity at impact? s(t) = – 16 t 2 + 16 t + 32 Position function The velocity at time t is given by the derivative s (t) = – 32 t + 16. So, the velocity at time is t = 2 is s (2) = – 32(2) + 16 = – 48 feet per second. 33

Add on to Notes #A To estimate the height of a building, a stone is dropped from the top of the building into a pool of water at ground level. How high is the building if the splash is seen 7. 0 seconds after the stone is dropped? Use the position function for free-falling objects given below. (Round your answer to one decimal place. ) s(t) = – 4. 9 t 2 + v 0 t + s 0 Dropped v 0 = = 0 Position Equation: s(t) = – 4. 9 t 2 + s 0 The height is zero when t = 7. 0 sec: S(7. 0) = 0 – 4. 9(7. 0)2 + s 0 = 0 s 0 = 240. 1 meters The volume of a cube with sides of length s is given by V = s 3. Find the rate of change of the volume with respect to s when s = 3 centimeters. Rate of Change = Derivative V = s 3 dv/ = 3 s 2 ds dv/ = 3(3)2 = 27 ds 34

2. 2 Summary Objectives n Find the derivative of a function using the Constant Rule. n Find the derivative of a function using the Power Rule. n Find the derivatives of the sine function and of the cosine function. n Use derivatives to find rates of change. The average velocity is d/ d/ dx (sin x) = cosx dx (cos x) = -sinx Position Function: s(t) = ½ gt 2 + v 0 t + s 0 Velocity Function: v(t) = s′(t) Copyright © Cengage Learning. All rights reserved. 35

2. 3 Product and Quotient Rules and Higher-Order Derivatives Objectives n Find the derivative of a function using the Product Rule. n Find the derivative of a function using the Quotient Rule. n Find the derivative of a trigonometric function. n Find a higher-order derivative of a function. Copyright © Cengage Learning. All rights reserved. 36

The Product Rule 37

Example 1 – Using the Product Rule Find the derivative of 3 x – 2 x 2 5 + 4 x 3 – 4 x 4 h′(x) = (3 x – 2 x 2)(4) + (5 + 4 x)(3 – 4 x) = 12 x – 8 x 2 + 15 – 8 x – 16 x 2 = – 24 x 2 + 4 x + 15 38

Example 2 – Using the Product Rule Find the derivative of y = 3 x 2 sinx 3 x 2 sinx y′ = (3 x 2)(cosx) + (sinx)(6 x) 6 x cosx = 3 x 2 cosx + 6 x sinx Find the derivative of y = 2 x cosx – 2 sinx 2 x cosx y′ = (2 x)(-sinx) + (cosx)(2) – 2 cosx 2 -sinx = – 2 x sinx + 2 cosx – 2 cosx = – 2 x sinx 39

Example 3 – Using the Quotient Rule Find the derivative of Lo: x 2 + 1 d. Lo: 2 x Hi: 5 x – 2 d. Hi: 5 y′ 40

Example 4 – Using the Quotient Rule Find the equation of the tangent line to the graph of f(x) at x = -1 We need the point and slope of the tangent line at x = -1 The point: find f(-1) The point is (-1, 1) The slope: find f′(-1) Lo: x + 5 d. Lo: 1 Hi: 3 – 1/x = 3 – x-1 d. Hi: 1 x-2 = 1/x 2 The equation of the tangent line at ( -1, 1) is y = 1 41

Ex 5 – Not every Quotient needs Quotient Rule Find the derivative of each 42

Proof of the Derivative of Tanx Find the Derivative of tan x using the derivatives of sin x and cos x Reminder from section 2. 2 d(sin x) = cos x d(cos x) = -sin x Extra Credit for proving 43 derivatives of all six trig functions

Proof of the Derivative of Cscx Find the Derivative of csc x using the derivatives of sin x and cos x Reminder from section 2. 2 d(sin x) = cos x d(cos x) = -sin x Extra Credit for proving 44 derivatives of all six trig functions

Derivatives of Trigonometric Functions 10 bonus points in the test category for proving the derivatives of all six trig functions. Example 6 45

Higher-Order Derivatives Higher-order derivatives are denoted as follows. 46

Higher-Order Derivatives Just as you can obtain a velocity function by differentiating a position function, you can obtain an acceleration function by differentiating a velocity function. Another way of looking at this is that you can obtain an acceleration function by differentiating a position function twice. 47

Example 10 – Finding the Acceleration Due to Gravity Because the moon has no atmosphere, a falling object on the moon encounters no air resistance. In 1971, astronaut David Scott demonstrated that a feather and a hammer fall at the same rate on the moon. The position function for each of these falling objects is given by s(t) = – 0. 81 t 2 + 2 where s(t) is the height in meters and t is the time in seconds. What is the ratio of Earth’s gravitational force to the moon’s? s(t) = – 0. 81 t 2 + 2 Position function s'(t) = – 1. 62 t Velocity function s"(t) = – 1. 62 Acceleration function So, the acceleration due to gravity on the moon is – 1. 62 meters per sec 48

Ex 11 – use the nderiv button on calculator A population of 490 bacteria is introduced into a culture and grows in number according to the equation below, where t is measured in hours. Find the rate at which the population is growing when t = 3. (Round your answer to two decimal places. ) ( ( ) ) Answer: 23. 75 bacteria/hour 49

2. 3 Summary Objectives n Find the derivative of a function using the Product Rule. n Find the derivative of a function using the Quotient Rule. n Find the derivative of a trigonometric function. n Find a higher-order derivative of a function. d(sinx) = cosx d(tanx) = sec 2 x d(secx) = secxtanx d(cosx) = –sinx d(cotx) = –csc 2 x d(cssx) = –cscxcotx Position Function: s(t) = ½ gt 2 + v 0 t + s 0 Velocity Function: v(t) = s′(t) Acceleration Function: a(t) = v′(t) = s′′(t) 50 Copyright © Cengage Learning. All rights reserved.

2. 4 The Chain Rule Objectives n Find the derivative of a composite function using the Chain Rule. n Find the derivative of a function using the General Power Rule. n Simplify the derivative of a function using algebra. n Find the derivative of a trigonometric function using the Chain Rule. Copyright © Cengage Learning. All rights reserved. 51

The Chain Rule This text has yet to discuss one of the most powerful differentiation rules—the Chain Rule. This rule deals with composite functions and adds a surprising versatility to the rules discussed in the two previous sections. For example, compare the functions shown below. 52

Example 2 – Using the Chain Rule Find dy/dx for y = (x 2 + 1)6 You could take the binomial and raise it the sixth power then take the derivative but that would be time consuming. Using the Chain Rule is much quicker and efficient method for finding the derivative. Think of the Chain Rule as the reverse of the order of operations. By order of operations we would first find the value of x 2 + 1 (junk)6 dy/dx = 6(junk)5 d(x 2 + 1) = 6(x 2 + 1)5(2 x) = 12 x(x 2 + 1)5 53

Example 3 & 4 – Using the Chain Rule Find the derivative of f(x) = (3 x – 2 x 2)3. Order of operations: 3 x – 2 x 2 (junk)3 f′(x) = 3(junk)2 d(3 x – 2 x 2) = 3(3 x – 2 x 2)2(3 – 4 x) Find the derivative of Order of operations: x 2 – 1 (junk)2/3 y′ = 2/3(junk)– 1/3 d(x 2 – 1) = 2/3(x 2 – 1)– 1/3 (2 x) 54

Example 5 – Using the Chain Rule Find the derivative of First re-write the function Order of operations: 2 t – 3 -7(junk)– 2 g′(t) = 14(junk)– 3 d(2 t – 3) = 14(2 t – 3)– 3 (2) 55

Simplifying Derivatives The next three examples illustrate some techniques for simplifying the “raw derivatives” of functions involving products, quotients, and composites. 56

Example 6 – Combining Several Rules What is the GCF? 57

Example 7 – Combining Several Rules 58

Example 8 – Combining Several Rules 59

Trigonometric Functions and the Chain Rule The “Chain Rule versions” of the derivatives of the six trigonometric functions are as follows. d(sin u) = cos u du d(tan u) = sec 2 u du d(sec u) = sec u tan u du d(cos u) = –sin u du d(cot u) = –csc 2 u du d(csc u) = –csc u cot u du 60

Example 9 – Applying the Chain Rule to Trigonometric Functions Find the derivative of each: a. y = sin 2 x Order of operations: 2 x sin(junk) b. y = cos(x – 1) Order of operations: x – 1 cos(junk) c. y = tan 3 x Order of operations: 3 x tan(junk) y′ = cos(2 x) d(2 x) y′ = 2 cos 2 x y′ = –sin(x – 1) d(x - 1) y′ = – sin(x – 1) y′ = sec 2(3 x) d(3 x) y′ = 3 sec 2(3 x) 61

Ex 10 – More Complicated Find the derivative of each: a. y = cos 3 x 2 y = cos (3 x 2) y′ = –sin (3 x 2) d(3 x 2) y′ = – 6 x sin (3 x 2) b. y = cos(3)x 2 c. y = cos (3 x)2 cos(3) is a # (just a coef of x 2) y′ = 2 cos(3)x y = cos (9 x 2) y′ = –sin (9 x 2) d(9 x 2) y′ = – 18 x sin (9 x 2) d. y = cos 2 x y = (cos x)2 y′ = 2(cos x)1 d(cos x) y′ = – 2 cos x sin x e. y y = (cos x)1/2 y′ = ½ (cos x)– 1/2 d(cos x) 62

Ex 11 – Even More Complicated Find the derivative of f(t) = sin 3 4 t = (sin (4 t))3 Order of operations 4 t sin(junk) (stuff)3 Derivative in reverse order 3(stuff)2 cos(junk) d(4 t) f′(t) = 3(sin (4 t))2 d(sin (4 t)) = 3 sin 2(4 t) cos(4 t) d(4 t) = 3 sin 2(4 t) cos(4 t) (4) f′(t) = 12 sin 2(4 t) cos(4 t) 63

2. 4 Summary Objectives n Find the derivative of a composite function using the Chain Rule. n Find the derivative of a function using the General Power Rule. n Simplify the derivative of a function using algebra. n Find the derivative of a trigonometric function using the Chain Rule. Copyright © Cengage Learning. All rights reserved. 64

2. 5 Implicit Differentiation Objectives n Distinguish between functions written in implicit form and explicit form. n Use implicit differentiation to find the derivative of a function. Introduction: Notes on whiteboard: Find d/dx [3 x 2] d/dx [4 x 3 + 4 y 5 – 3 x 2] d/da [4 y 2 – 2 x 5 + 3 a 4] Copyright © Cengage Learning. All rights reserved. 65

Implicit and Explicit Functions Most functions have been expressed in explicit form. For example, in the equation Explicit form the variable y is explicitly written as a function of x. 66

Implicit and Explicit Functions Suppose you were asked to find dy/dx for this equation. You could begin by writing y explicitly as a function of x and then differentiating. This strategy works whenever you can solve for the function explicitly. You cannot, however, use this procedure when you are unable to solve for y as a function of x. 67

Implicit and Explicit Functions For instance, how would you find dy/dx for the equation where it is very difficult to express y as a function of x explicitly? To find dy/dx, you can use implicit differentiation. 68

Implicit and Explicit Functions To understand how to find dy/dx implicitly, you must realize that the differentiation is taking place with respect to x. This means that when you differentiate terms involving x alone, you can differentiate as usual. However, when you differentiate terms involving y, you must apply the Chain Rule, because you are assuming that y is defined implicitly as a differentiable function of x. 69

Example 1 – Differentiating with Respect to x 70

Example 1 – Differentiating with Respect to x cont’d 71

Implicit Differentiation 72

Example 2 – Implicit Differentiation Find dy/dx given that y 3 + y 2 – 5 y – x 2 = – 4. 1. Differentiate both sides of the equation with respect to x. 2. Collect the dy/dx terms on the left side of the equation and move all other terms to the right side of the equation. 3. Factor dy/dx out of the left side of the equation. 4. Solve for dy/dx by dividing by (3 y 2 + 2 y – 5). 73

Implicit Differentiation To see how you can use an implicit derivative, consider the graph shown in Figure 2. 27. From the graph, you can see that y is not a function of x. Even so, the derivative found in Example 2 gives a formula for the slope of the tangent line at a point on this graph. The slopes at several points on the graph are shown below the graph. Figure 2. 27 y 3 + y 2 – 5 y – x 2 = – 4 74

Ex 4 – Finding the Slope of a Graph Find the slope of the tangent line to the graph of x 2 + 4 y 2 = 4 at the point 2 x + 8 y dy/dx = 0 8 y dy/dx = – 2 x dy/ = -2 x/8 y dx dy/ = -x/4 y dx 75

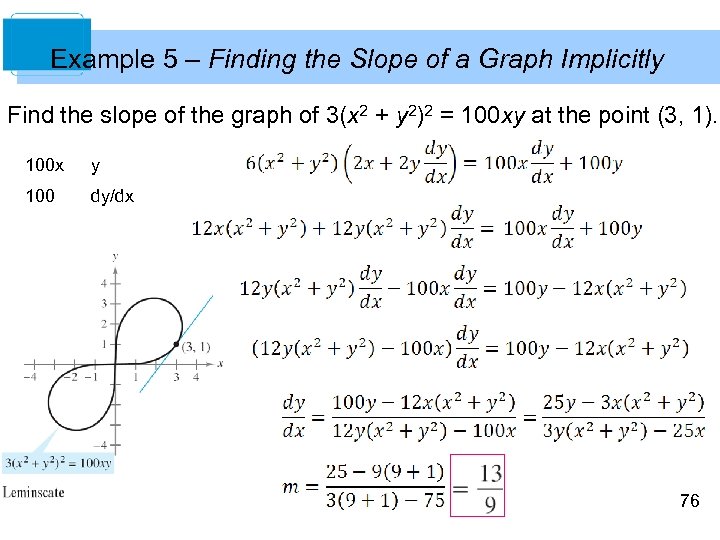Example 5 – Finding the Slope of a Graph Implicitly Find the slope of the graph of 3(x 2 + y 2)2 = 100 xy at the point (3, 1). 100 x y 100 dy/dx 76

Example 7 Find the Second Derivate Implicitly Given x 2 + y 2 = 25, find 2 x + 2 y dy/dx = 0 2 y dy/dx = -2 x dy/ = -2 x/2 y dx dy/ = -x/y dx Now find the derivative of dy/ x dx = - /y using quotient rule Lo: y Hi: -x d. Lo: dy/dx = -x/y d. Hi: -1 77

Ex 8 – Find a Tangent Line to a Graph Find the tangent line to the graph given by x 2(x 2 + y 2) = y 2 at the point 78

2. 5 Summary Objectives n Distinguish between functions written in implicit form and explicit form. n Use implicit differentiation to find the derivative of a function. Copyright © Cengage Learning. All rights reserved. 79

Finding Related Rates The Chain Rule can be used to find dy/dx implicitly. Another important use of the Chain Rule is to find the rates of change of two or more related variables that are changing with respect to time. 81

Finding Related Rates For example, when water is drained out of a conical tank (see Figure 2. 33), the volume V, the radius r, and the height h of the water level are all functions of time t. Knowing that these variables are related by the equation Figure 2. 33 82

Finding Related Rates you can differentiate implicitly with respect to obtain the related-rate equation From this equation you can see that the rate of change of V is related to the rates of change of both h and r. 83

Example 1 – Two Rates That Are Related Suppose x and y are both differentiable functions of t and are related by the equation y = x 2 + 3. Find dy/dt when x = 1, given that dx/dt = 2 when x = 1. Differentiate both sides of the equation with respect to t. When x = 1 and dx/dt = 2, you have 84

Problem Solving with Related Rates 85

Example 2 – Ripples in a Pond A pebble is dropped into a calm pond, causing ripples in the form of concentric circles. The radius r of the outer ripple is increasing at a constant rate of 1 foot per second. When the radius is 4 feet, at what rate is the total area of the disturbed water changing? Given: Find: When: dr/dt = 1 ft/sec d. A/dt r = 4 ft Equation: A = πr 2 d. A/dt = 2πr dr/dt d. A/dt = 2π(4)(1) d. A/dt = 8π 86

Example 3 – An Inflating Balloon Air is being pumped into a spherical balloon (see Figure 2. 35) at a rate of 4. 5 cubic feet per minute. Find the rate of change of the radius when the radius is 2 feet. Given: Find: When: r = 2 Equation: 9/ dr/ Figure 2. 35 2 = 4π(2) 2 dr/ dt = 9/32π ≈ 0. 09 ft/min dt 87

Ex 4 – Sand Falling into a Conical Pile At a sand & gravel plant, sand is falling off a conveyor and onto a conical pile at a rate of 6 cubic feet per minute. The diameter of the base of the cone is approximately three times the altitude. At what rate is the height of the pile changing when the pile is 4 feet high? Given: Find: When: d. V/dt = 6 ft/min dh/dt h = 4 ft Equation: V = 1/3 πr 2 h d = 3 h 2 r = 3 h r = 3/2 h r 2 = 9/4 h 2 d. V/dt = 9/4 πh 2 dh/dt V = 1/3 π(9/4 h 2)h 6 = 9/4 π(4)2 dh/dt V = 3/4 πh 3 6 = 36π dh/dt = 1/6π ft/min 88

Ex 5 – Fishing A fish is reeled in at a rate of 2. 9 feet per second from a point 10 feet above the water (see figure). At what rate is the angle between the line and the water changing when there is a total of 25 feet of line out? (Round your answer to three decimal places. ) Given: Find: When: dx/dt = -2. 9 ft/sec dθ/dt x = 25 ft Equation: When: Sin θ = 10/x Sin θ = 10 x– 1 Cos θ dθ/dt = – 10 x– 2 dx/dt x = 25 ft dθ/dt ≈ 0. 051 rad/sec 89

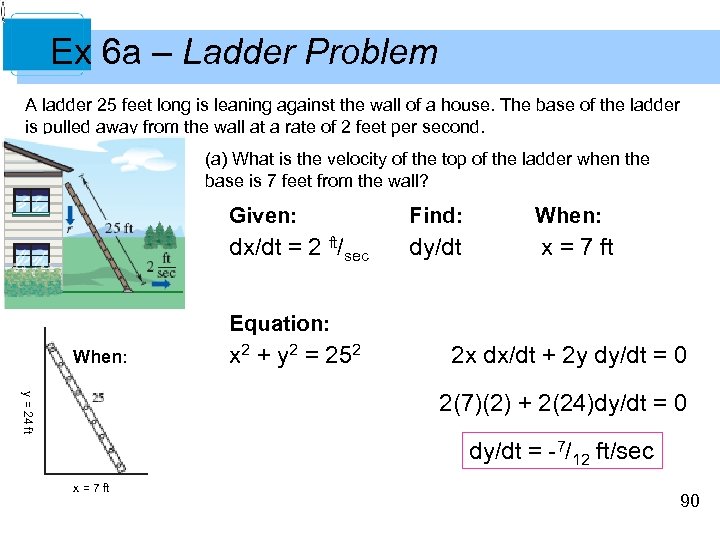Ex 6 a – Ladder Problem A ladder 25 feet long is leaning against the wall of a house. The base of the ladder is pulled away from the wall at a rate of 2 feet per second. (a) What is the velocity of the top of the ladder when the base is 7 feet from the wall? Given: Find: When: dx/dt = 2 ft/sec dy/dt x = 7 ft Equation: When: x 2 + y 2 = 252 2 x dx/dt + 2 y dy/dt = 0 y = 24 ft 2(7)(2) + 2(24)dy/dt = 0 dy/dt = -7/12 ft/sec x = 7 ft 90

Ex 6 – Ladder Problem A ladder 25 feet long is leaning against the wall of a house. The base of the ladder is pulled away from the wall at a rate of 2 feet per second. (b) Consider the triangle formed by the side of the house, ladder, and the ground. Find the rate at which the area of the triangle is changing when the base of the ladder is 7 feet from the wall. Given: Find: When: dx/dt = 2 ft/sec d. A/dt x = 7 ft dy/dt = -7/12 ft/sec ←from part a When: Equation: A = ½ xy y = 24 ft x = 7 ft d. A/dt = 527/24 ft 2/sec 91

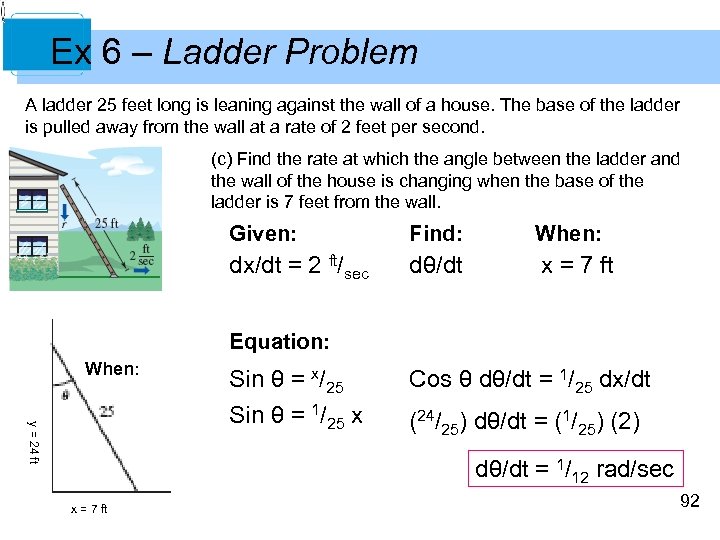Ex 6 – Ladder Problem A ladder 25 feet long is leaning against the wall of a house. The base of the ladder is pulled away from the wall at a rate of 2 feet per second. (c) Find the rate at which the angle between the ladder and the wall of the house is changing when the base of the ladder is 7 feet from the wall. Given: Find: When: dx/dt = 2 ft/sec dθ/dt x = 7 ft Equation: When: y = 24 ft Sin θ = x/25 Sin θ = 1/25 x Cos θ dθ/dt = 1/25 dx/dt (24/25) dθ/dt = (1/25) (2) dθ/dt = 1/12 rad/sec x = 7 ft 92