2 D and 3 D Fourier Based Discrete

2 D and 3 D Fourier Based Discrete Radon Transform Amir Averbuch With Ronald Coifman – Yale University Dave Donoho – Stanford University Moshe Israeli – Technion, Israel Yoel Shkolnisky – Yale University

$Research Activities • Polar processing (Radon, MRI, diffraction tomography, polar processing, image processing) •$

Research Activities • Polar processing (Radon, MRI, diffraction tomography, polar processing, image processing) • Dimensionality reduction (hyperspectral processing, segmentation and sub-pixel segmentation, remote sensing, performance monitoring, data mining) • Wavelet and frames (error correction, compression) • Scientific computation (prolate spheroidal wave functions) • XML (fast Xpath, handheld devices, compression) • Nano technology (modeling nano batteries, controlled drug release, material science simulations) interdisciplinary research with material science, medicine, biochemistry, life sciences

Participants: previous and current • • • Dr Yosi Keller – Gibbs Professor, Yale Yoel Shkolnisky - Gibbs Professor, Yale Tamir Cohen – submitted his Ph. D Shachar Harrusi – Ph. D student Ilya Sedelnikov - Ph. D student Neta Rabin - Ph. D student Alon Shekler - Ph. D student Yossi Zlotnick - Ph. D student Nezer Zaidenberg - Ph. D student Zur Izhakian – Ph. D student

Computerized tomography

CT-Basics

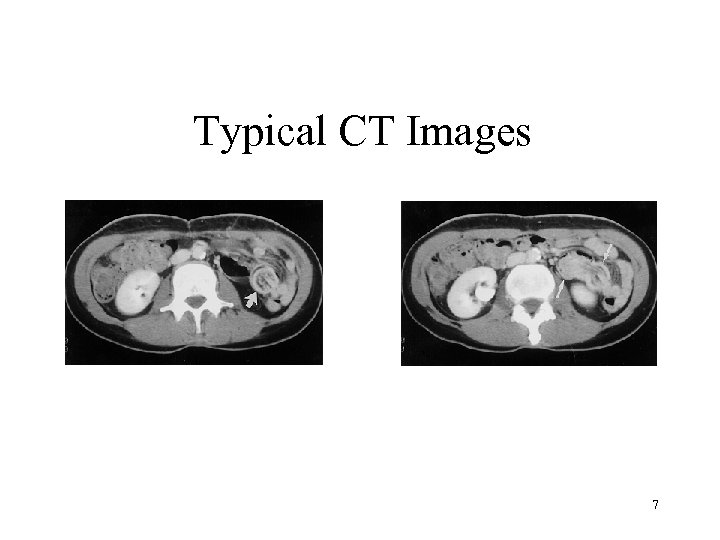
Typical CT Images 7

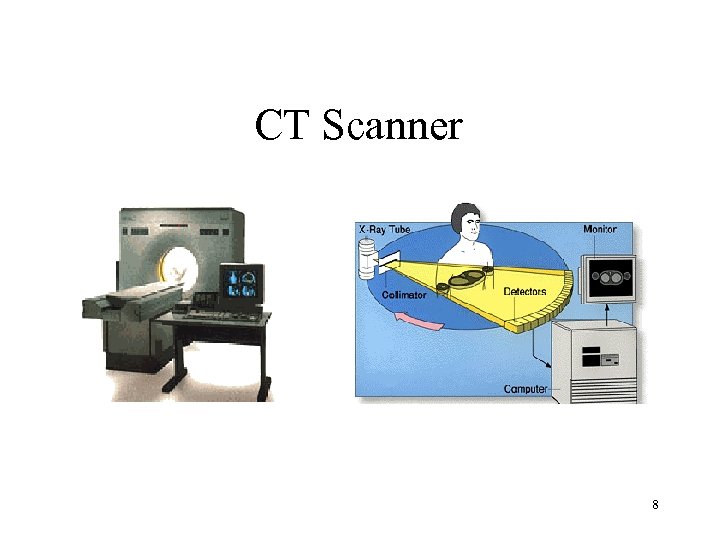
CT Scanner 8

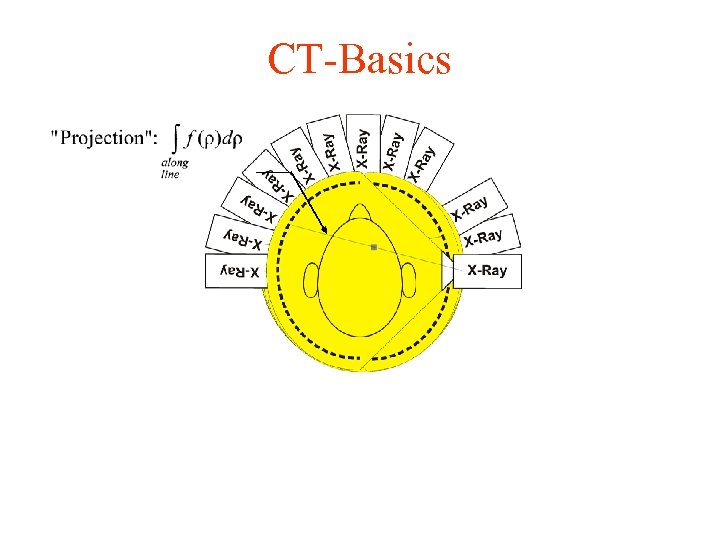
CT-Basics

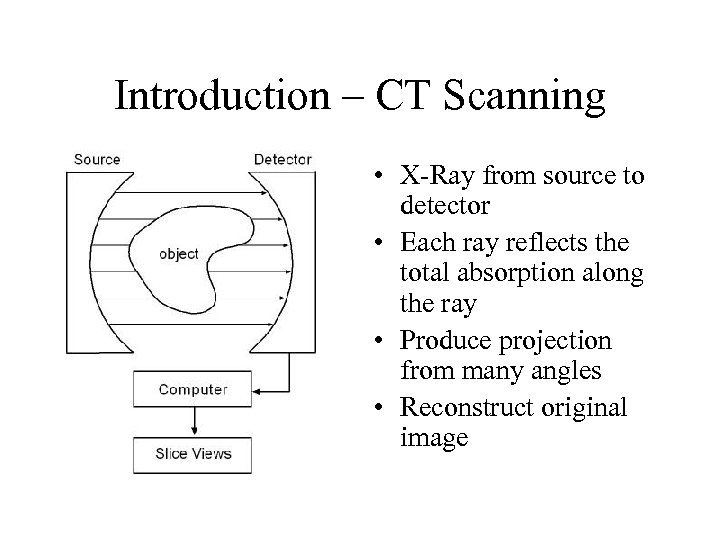
Introduction – CT Scanning • X-Ray from source to detector • Each ray reflects the total absorption along the ray • Produce projection from many angles • Reconstruct original image

2 D Continuous Radon Transform The 2 D continuous Radon is defined as

2 D Continuous Fourier Slice Theorem 2 D Fourier slice theorem where is the 2 D continuous Fourier transform of f. The 1 D Fourier transform with respect to s of equal to a central slice, at angle θ, of the 2 D Fourier transform of the function f(x, y). is

Discretization Guidelines We will look for both 2 D and 3 D definitions of the discrete Radon transform with the following properties: • Algebraic exactness • Geometric fidelity • Rapid computation algorithm • Invertibility • Parallels with continuum theory

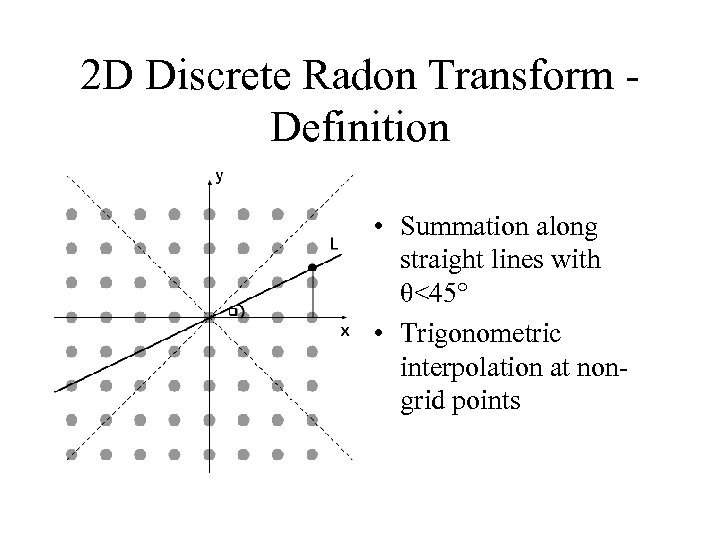
2 D Discrete Radon Transform Definition • Summation along straight lines with θ<45° • Trigonometric interpolation at nongrid points

2 D Discrete Radon Transform – Formal Definition For a line we define where and is the Dirichlet kernel with

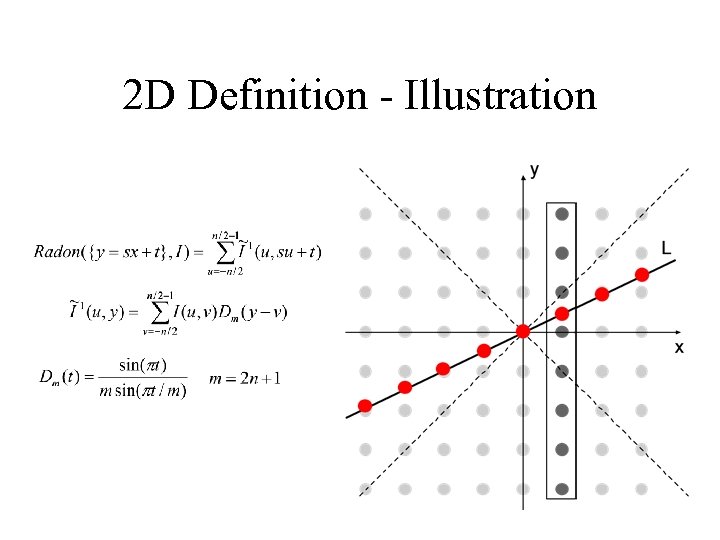
2 D Definition - Illustration

2 D Discrete Radon Definition – Cont. For a line where and we define

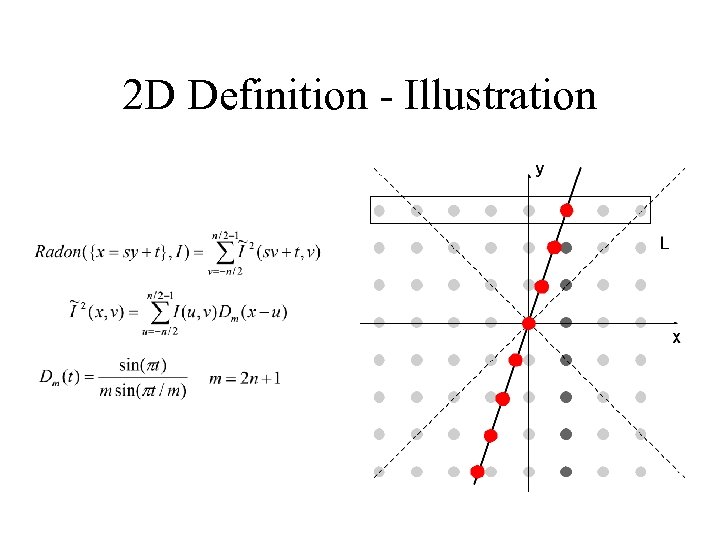
2 D Definition - Illustration

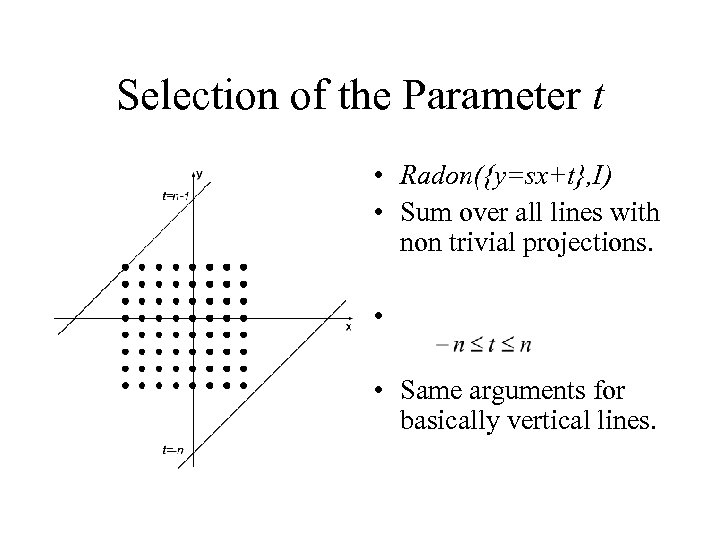
Selection of the Parameter t • Radon({y=sx+t}, I) • Sum over all lines with non trivial projections. • • Same arguments for basically vertical lines.

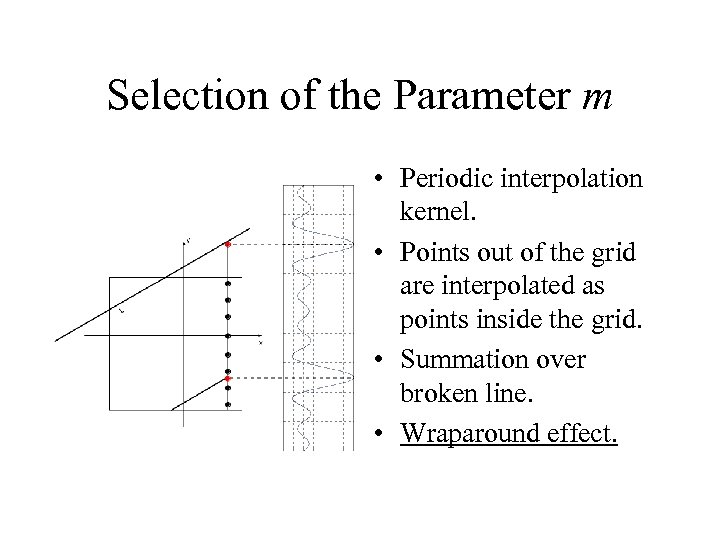
Selection of the Parameter m • Periodic interpolation kernel. • Points out of the grid are interpolated as points inside the grid. • Summation over broken line. • Wraparound effect.

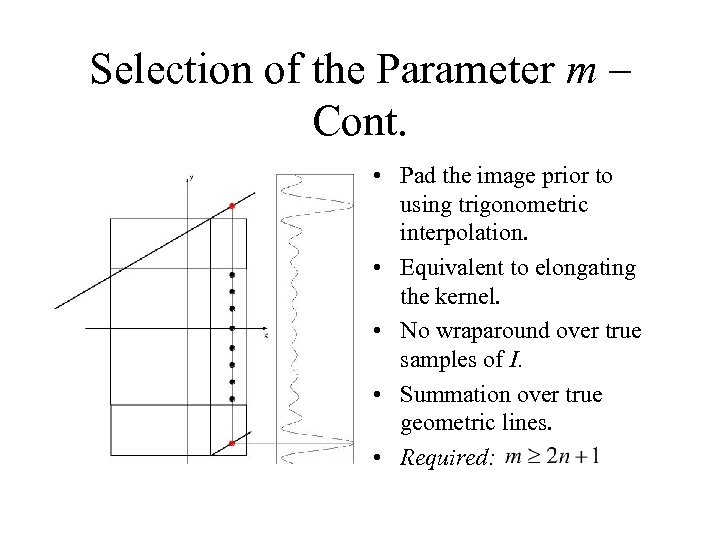
Selection of the Parameter m – Cont. • Pad the image prior to using trigonometric interpolation. • Equivalent to elongating the kernel. • No wraparound over true samples of I. • Summation over true geometric lines. • Required:

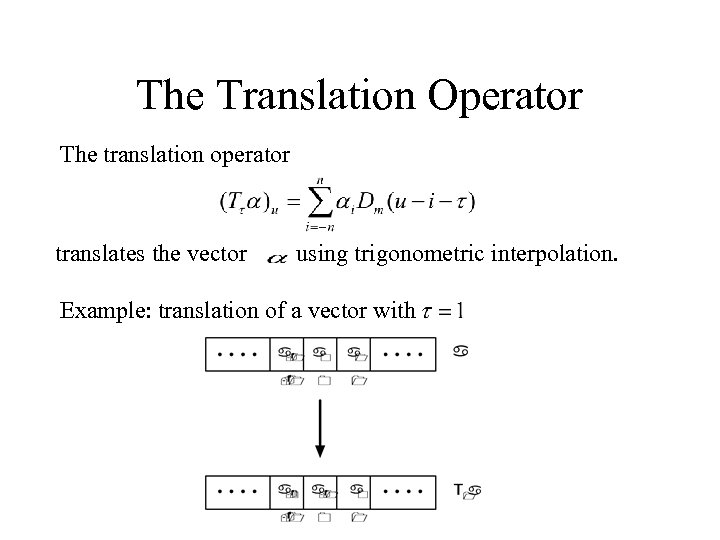
The Translation Operator The translation operator translates the vector using trigonometric interpolation. Example: translation of a vector with

The Shearing Operator For the slope θ of a basically horizontal line: For the slope θ of a basically vertical line: Motivation: The shearing operator translates the samples along an inclined line into samples along horizontal/vertical line.

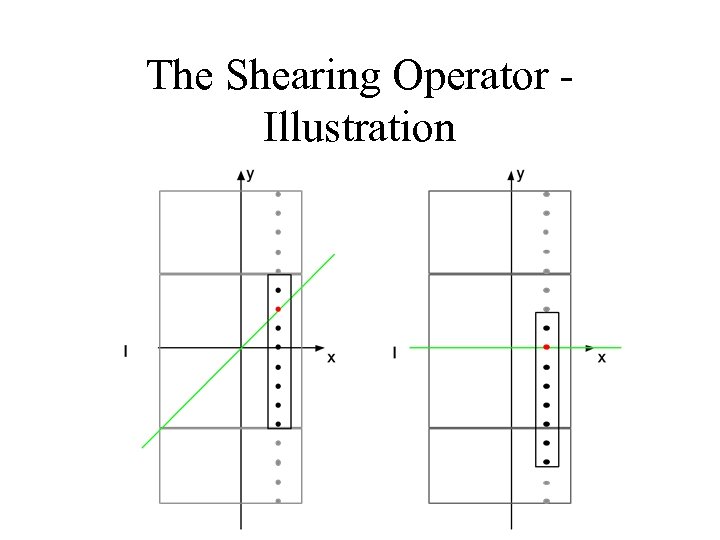
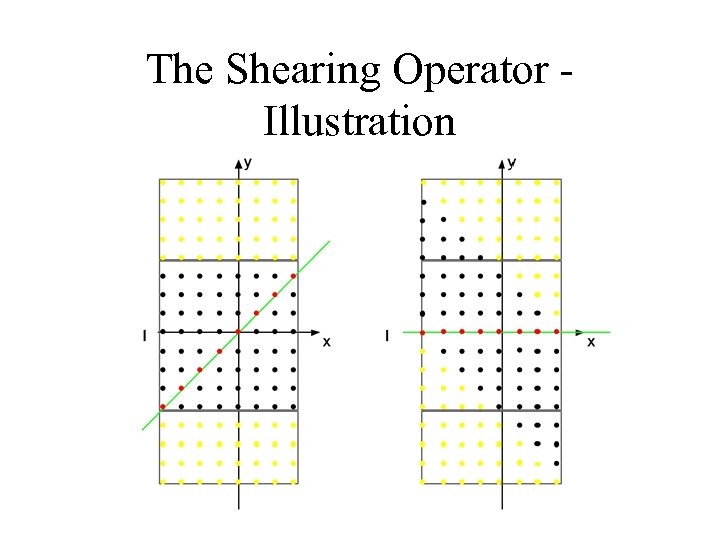
The Shearing Operator Illustration

Alternative Definition of the Discrete Radon Transform and are padded versions of the x-axis respectively along the y-axis and

2 D Discrete Fourier Slice Theorem Using the alternative discrete Radon definition we prove: where

Discretization of θ • The discrete Radon transform was defined for a continuous set of angles. • For the discrete set Θ the discrete Radon transform is discrete in both Θ and t. • For the set Θ, the Radon transform is rapidly computable and invertible.

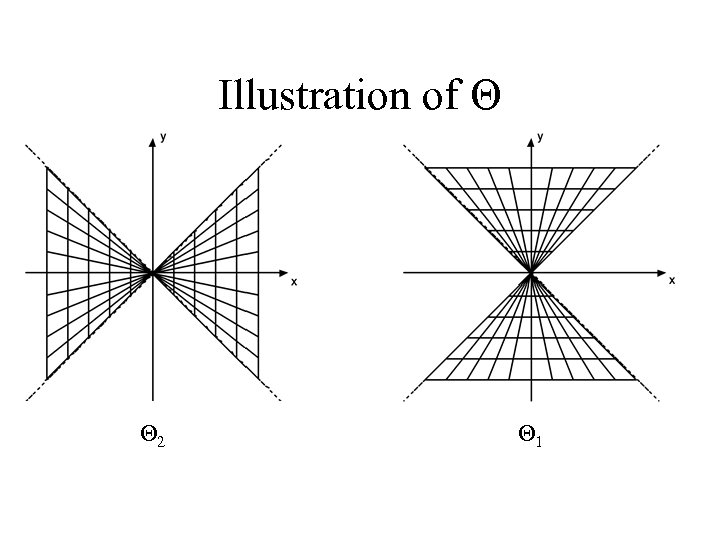
Illustration of Θ Θ 2 Θ 1

Fourier Slice Theorem Revisited For where We define the pseudo-polar Fourier transform:

The Pseudo-Polar Grid The pseudo polar Fourier transform is the sampling of special pointset called the pseudo-polar grid. The pseudo-polar grid is defined by on a

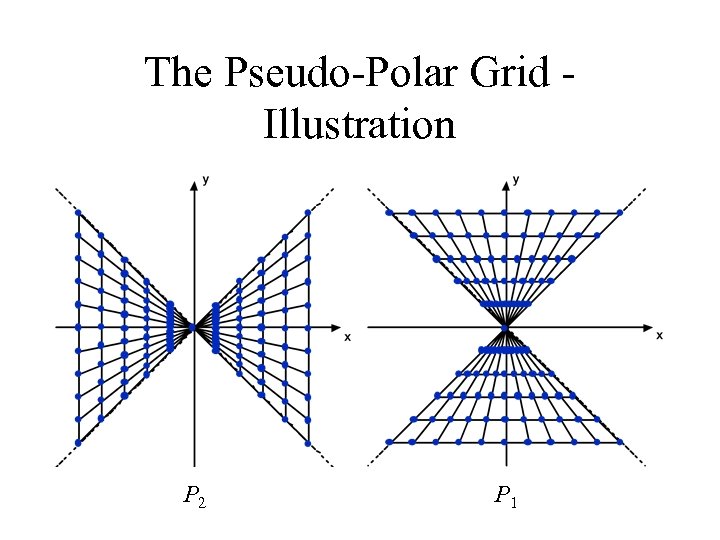
The Pseudo-Polar Grid Illustration P 2 P 1

The Pseudo-Polar Grid Illustration

$The Fractional Fourier Transform The fractional Fourier transform is defined as Can be computed$

The Fractional Fourier Transform The fractional Fourier transform is defined as Can be computed for any using operations. We can use the fractional Fourier transform to compute samples of the Fourier transform at any spacing.

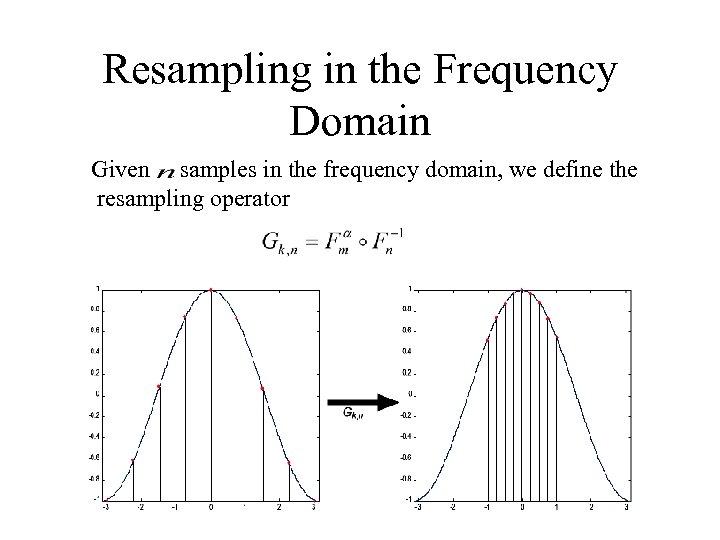
Resampling in the Frequency Domain Given samples in the frequency domain, we define the resampling operator

2 D Discrete Radon Algorithm • Given we can compute using operations by using 1 D Fourier transform. • We show an for computing Gk, n .

2 D Discrete Radon Algorithm – Cont. Description: (PP 1 I) 1. Pad both ends of the y-direction of the image I and compute the 2 D DFT of the padded image. The results are placed in I’. 2. Resample each row k in I’ using the operator Gk, n with α = 2 k/n. 3. Flip each row around its center.

Papers http: //www. math. tau. ac. il/~amir http: //pantheon. yale. edu/~yk 253/ • • • • • Optical Snow Analysis using the 3 D-Xray Transform, submitted. Fast and Accurate Polar Fourier Transform, submitted. Discrete diffraction tomography, submitted. 2 D Fourier Based Discrete Radon Transform, submitted. Algebraically accurate 3 -D rigid registration, IEEE Trans. on Signal Proessing. Algebraically Accurate Volume Registration using Euler's Theorem and the 3 -D Pseudo-Polar FFT, submitted. Fast Slant Stack: A notion of Radon Transform for Data in a Cartesian Grid which is Rapidly Computible, Algebraically Exact, Geometrically Faithful and Invertible, SIAM Scientific Computing. Pseudo-polar based estimation of large translations, rotations and scalings in images, IEEE Trans. on Image Processing. The Angular Difference Function and its application to Image Registration, IEEE PAMI. 3 D Discrete X-Ray Transform, Applied and Computational Harmonic Analysis 3 D Fourier Based Discrete Radon Transform, Applied and Computational Harmonic Analysis Digital Implementation of Ridgelet Packets, Beyond wavelets – chapter in book. Multidimensional discrete Radon transform, chapter in book. The pseudopolar FFT and its Applications, Research Report A signal processing approach to symmetry detection, IEEE Trans. on Image Processing Fast and accurate pseudo-polar protein docking, submitted.