cd471fa74a2065a7e4fbd69444973ade.ppt
- Количество слайдов: 124

2. C – Conserving Matter

Objectives State and apply the Law of Conservation of Matter. ¢ Learn how to balance chemical equations. ¢ Explain the mole concept. ¢ Calculate molar mass of a compound. ¢ Calculate percent composition of elements. ¢ Distinguish between renewable and nonrenewable resources. ¢

C. 1: Keeping Track of Atoms ¢ Complete the reading guide handout

C. 1: Keeping Track of Atoms In some chemical reactions, matter seems to be created. ¢ When a nail rusts. ¢ In other reactions, matter seems to disappear. ¢ When paper burns and apparently vanishes ¢ However, neither creation or destruction of matter occurs. ¢ Matter may undergo physical or chemical changes. ¢

C. 1: Keeping Track of Atoms In a car engine gasoline is burned. What happens to the molecules of gasoline? ¢ Gasoline is made up of carbon and hydrogen atoms (C and H atoms) ¢ When gasoline burns these atoms react with oxygen atoms in air to form carbon dioxide (CO 2), carbon monoxide (CO) and water (H 2 O). ¢ The original atoms of gasoline are not destroyed but become rearranged. ¢
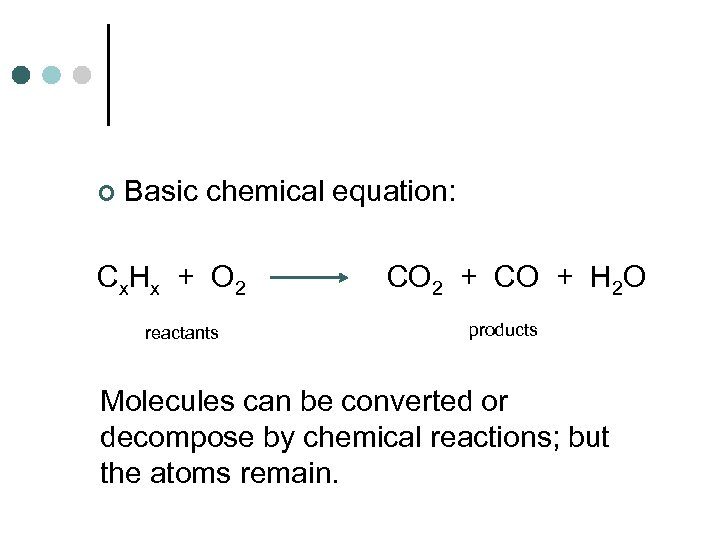
¢ Basic chemical equation: Cx. Hx + O 2 reactants CO 2 + CO + H 2 O products Molecules can be converted or decompose by chemical reactions; but the atoms remain.

C. 1: Keeping Track of Atoms Law of Conservation of Matter: Matter is neither created nor destroyed. ¢ Since chemical reactions cannot create or destroy atoms, chemical equations representing the reactions must always be BALANCED. ¢ This means that the number of atoms of each element is the same on the reactant and product sides of a chemical equation. ¢
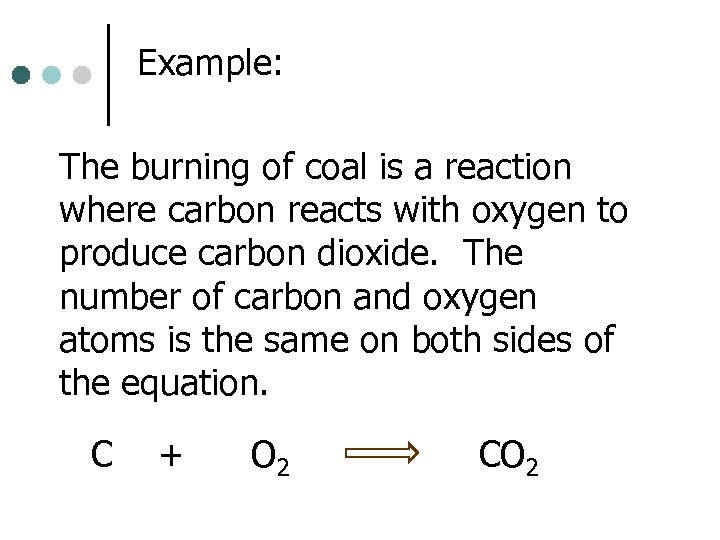
Example: The burning of coal is a reaction where carbon reacts with oxygen to produce carbon dioxide. The number of carbon and oxygen atoms is the same on both sides of the equation. C + O 2 CO 2

Atomic Perspective: C 1 Carbon atom O 2 1 oxygen molecule CO 2 1 carbon dioxide molecule 1. What are the reactants in this chemical equation? 2. What are the products in this chemical equation? 3. Are the same number of atoms on both sides of the equation? a. Were any atoms destroyed or created? b. Was the Law of Conservation of Matter maintained?

Atomic Perspective: Cu (s) + O 2 (g) Cu. O (s) From the burning of copper lab: Is this reaction balanced? Does it obey the Law of Conservation of Matter?

2 Cu (s) + O 2 (g) 2 Cu. O (s) COEFFICIENTS - indicates the number of units of each substance involved. 1. Does the oxygen molecule have a coefficient? 2. What do the subscripts represent? 3. Can subscripts be removed from chemical equations? The above reaction reads: 2 copper atoms react with 1 oxygen to produce 2 molecules of copper oxide.

C. 2: Accounting for Atoms To obey the Law of Conservation of Matter atoms can not be created or destroyed. All atoms must be accounted for on both sides of the reaction arrow.

Accounting for Atoms Homework: ¢ Complete C 1 Supplement worksheet ¢ ¢ Due:

C. 2: Accounting for Atoms Classwork: ¢ Page 155 -157 ¢ Questions 1 -5, parts A, C and D only ¢

C. 3: Balancing Chemical Equations

Balancing Equations

Balancing Equations Law of Conservation of Atoms: l The number of atoms of each type of element must be the same on each side of the equation.

Balancing Equations ¢ Balancing l Balance hints: the metals first. l Balance the non metals next. l Save the oxygen and hydrogen atoms until the end.

How do we Balance Equations? Below is the chemical equation for the reaction of hydrogen gas with oxygen gas to produce water. H 2 + O 2 H 2 O Is this reaction balanced?

Balancing Equations Hydrogen + oxygen H 2 + O 2 water H 2 O Hydrogen and oxygen are diatomic elements. ¢ Their subscripts cannot be changed. ¢ The subscripts on water cannot be changed. ¢

Balancing Equation H 2 + O 2 ¢ Count H 2 O the atoms on each side. l Reactant side: 2 atoms H and 2 atoms O l Product side: 2 atoms H and 1 atom O

Balancing Equations H 2 + O 2 H 2 O ¢ If the subscripts cannot be altered, how can the atoms be made equal? ¢ Adjust the number of molecules by changing the coefficients.

Balancing Equations H 2 + O 2 ¢ ¢ 2 H 2 O Balance one atom at a time: Let’s start with balancing oxygen! Reactants: 2 atoms of H and 2 atoms of O Products: 4 atoms of H and 2 atoms of O H is no longer balanced!

Balancing Equations 2 H 2 + O 2 ¢ ¢ 2 H 2 O Now try to balance the hydrogens by placing a 2 in front of the reactant H 2 Reactant side: 4 atoms of H and 2 atoms of O Product side: 4 atoms of H and 2 atoms of O It’s Balanced!

How do we Balance Equations? Number of compounds in the reaction Coefficients 2 H 2 + O 2 2 H 2 O Subscripts # of atoms in a compound Subscripts can not be changed. Coefficients balance atoms in an equation

How to Balance By Inspection: 1 Make a table of elements _____ CH 4 + _____ O 2 _____H 2 O + _____ C O 2 Reactants C H O Products

How to Balance By Inspection: 2 Count the number of each element or ion on the reactants and products side. Don’t forget to add all the atoms of the same element together— even if it appears in more than one compound! _____ CH 4 + _____ O 2 _____H 2 O + _____ C O 2 Reactants Products C 1 1 H 4 2 O 2 3

How to Balance By Inspection: 3 Add coefficients to balance the numbers Each time you add a coefficient, update your table with the new quantities of each atom. _____ CH 4 + _____ O 2 _____ H 2 O + _____ C O 2 2 2 Reactants Products C 1 1 H 4 2 4 O 2 3 4 4

How to Balance By Inspection: 4 Place a “ 1” in any empty coefficient location Filling each coefficient location lets you and the grader know that you finished the problem rather than you left some blank because you weren’t done! _____ CH 4 + _____ O 2 _____ H 2 O + _____ C O 2 1 2 2 1 Reactants Products C 1 1 H 4 2 4 O 2 3 4 4
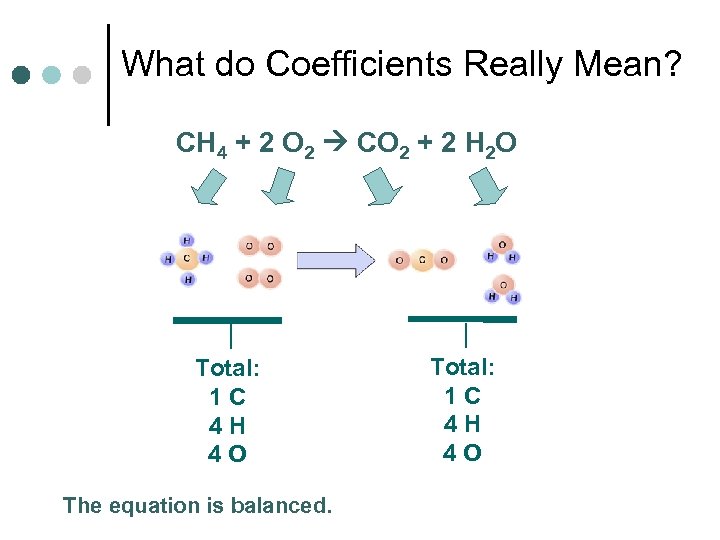
What do Coefficients Really Mean? CH 4 + 2 O 2 CO 2 + 2 H 2 O Total: 1 C 4 H 4 O The equation is balanced. Total: 1 C 4 H 4 O

Balancing Equations N 2 + H 2 Nitrogen + hydrogen ¢ Count NH 3 ammonia atoms. l Reactants: 2 atoms N and 2 atoms H l Products: 1 atom N and 3 atoms of H

Balancing Equations ¢ Nothing is balanced. ¢ Balance the nitrogen first by placing a coefficient of 2 in front of the NH 3. N 2 + H 2 2 NH 3

Balancing Equations Hydrogen is not balanced. ¢ Place a 3 in front of H 2. ¢ Reactant side: 2 atoms N, 6 atoms H ¢ Product side: 2 atoms N, 6 atoms H ¢ It’s balanced! ¢ N 2 + 3 H 2 2 NH 3

Balancing Equations Cu + H 2 SO 4 Cu. SO 4 + H 2 O + SO 2 Count Atoms: ¢ Reactants: Cu – 1, H – 2, S – 1, O – 4 ¢ Products: Cu – 1, H – 2, S - 2, O - 7 ¢

Balancing Equations ¢ Sulfur is not balanced. ¢ Place a two in front of sulfuric acid. ¢ Count Atoms: ¢ Reactants: Cu – 1, H – 4, S – 1, O – 8 ¢ Products: Cu – 1, H – 2, S - 2, O - 7 Cu + 2 H 2 SO 4 Cu. SO 4 + H 2 O + SO 2

Balancing Equations ¢ Hydrogen needs to be balanced so place a 2 in front of the H 2 O. ¢ Count the number of atoms. Cu + 2 H 2 SO 4 Cu. SO 4 + 2 H 2 O + SO 2

Balancing Equations Cu + 2 H 2 SO 4 Cu. SO 4 + 2 H 2 O + SO 2 Reactants: Cu – 1, H – 4, S – 2, O – 8 ¢ Products: Cu – 1, H – 4, S – 2, O – 8 ¢ ¢ It’s balanced!

Balancing Equations Ca 3(PO 4)2 + H 2 SO 4 ¢ Count Ca. SO 4 + H 3 PO 4 atoms. ¢ Reactants: Ca – 3 atoms, P – 2 atoms, O – 12 atoms, H – 2 atoms, S – 1 atom

Balancing Equations ¢ Side ¢ The note on Ca 3(PO 4)2 subscript after the phosphate indicates two phosphate groups. ¢ This means two P and eight O atoms.

Balancing Equations Ca 3(PO 4)2 + H 2 SO 4 ¢ Count Ca. SO 4 + H 3 PO 4 atoms in the product. ¢ Ca atoms – 1, S atom – 1, O atoms – 8; H atoms – 3, P atom – 1,

Balancing Equations ¢ Balance the metal first by placing a coefficient of 3 in front of Ca. SO 4. Ca 3(PO 4)2 + H 2 SO 4 3 Ca. SO 4 + H 3 PO 4

Balancing Equations ¢ Now balance the S atoms followed by the P atoms. Ca 3(PO 4)2 + 3 H 2 SO 4 3 Ca. SO 4 + H 3 PO 4

Balancing Equations ¢A coefficient of 2 placed in front of H 3 PO 4 which balances both hydrogen and phosphate. Ca 3(PO 4)2 + 3 H 2 SO 4 3 Ca. SO 4 + 2 H 3 PO 4

Balancing Equations ¢ This method of balancing equations is trial and error. ¢ Practice.
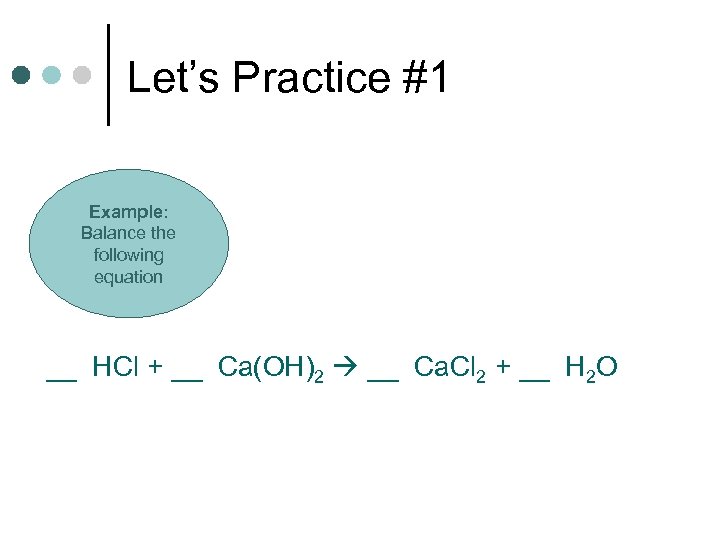
Let’s Practice #1 Example: Balance the following equation __ HCl + __ Ca(OH)2 __ Ca. Cl 2 + __ H 2 O

Let’s Practice #2 Example: Balance the following equation __ H 2 + __ O 2 __ H 2 O

Let’s Practice #3 Example: Balance the following equation __ Fe + __ O 2 ___ Fe 2 O 3

C. 4: Balancing Equations Classwork: ¢ Complete questions 1 -6 on page 160161 ¢ ¢ Due:

Balancing Equations Homework: ¢ Complete C 3 Supplement worksheet ¢ ¢ Due:

Balancing Equations ¢ Additional Worksheets

C. 5 The Mole Concept Definition: Mole – Unit for counting for chemists. Counting atoms is impractical because atoms are so small and are not visible to the naked eye. You can not weigh individual atoms on laboratory balance.

Relating Mass to Numbers of Atoms Introduction of three very important concepts: 1) The mole 2) Avogadro’s number 3) Molar mass

What is a counting unit? You’re already familiar with one counting unit…a “dozen” A dozen = 12 “Dozen” 12 A dozen doughnuts 12 doughnuts A dozen books 12 books A dozen cars 12 cars A dozen people 12 people

A Mole of Particles Contains 6. 02 x 1023 particles Avogadro’s Number 1 mole C = 6. 02 x 1023 C atoms 1 mole H 2 O = 6. 02 x 1023 H 2 O molecules 1 mole Na. Cl= 6. 02 x 1023 Na. Cl “molecules”

How big is a mole? ¢ ¢ Enough soft drink cans to cover the surface of the earth to a depth of over 200 miles. If you had Avogadro's number of unpopped popcorn kernels, and spread them across the United States of America, the country would be covered in popcorn to a depth of over 9 miles. If we were able to count atoms at the rate of 10 million per second, it would take about 2 billion years to count the atoms in one mole. One mole of paper clips would wrap around the earth 400 trillion times!

What does a “mole” count in? A mole = 6. 02 1023 (called Avogadro’s number) 6. 02 1023 = 602, 000, 000, 000 “mole” 6. 02 1023 1 mole of doughnuts 6. 02 1023 doughnuts 1 mole of atoms 6. 02 1023 atoms 1 mole of molecules 6. 02 1023 molecules

1. Mole of a substance = grams of substance/MW of substance 2. The mole enables chemists to move from the microscopic world of atoms and molecules to the real world of grams and kilograms.

Molar Mass

Definition Molar Mass – The mass for one mole of an atom or molecule. Other terms commonly used for the same meaning: Molecular Weight Atomic Weight (used for atoms)

Mass for 1 mole of atoms The average atomic mass = grams for 1 mole Average atomic mass is found on the periodic table Element Mass 1 mole of carbon atoms 12. 01 g 1 mole of oxygen atoms 16. 00 g 1 mole of hydrogen atoms 1. 01 g Unit for molar mass: g/mole or g/mol

One mole of carbon (12 grams) and one mole of copper (63. 5 grams)

Molar Mass Examples: Molar mass of lithium (Li) = 6. 94 g/mol Molar mass of helium (He) = 4. 00 g/mol Molar mass of mercury (Hg) = 200. 6 g/mol

Molar Mass A molar mass of an element contains one mole of atoms. 4. 00 g helium = 1 mole = 6. 02 x 1023 atoms. 6. 94 g lithium = 1 mole = 6. 02 x 1023 atoms. 200. 6 g mercury = 1 mole = 6. 02 x 1023 atoms.

Molar mass for molecules The molar mass for a molecule = the sum of the molar masses of all the atoms

Calculating a Molecule’s Mass To find the molar mass of a molecule: 1 Count the number of each type of atom 2 Find the molar mass of each atom on the periodic table 3 Multiple the # of atoms molar mass for each atom 4 Find the sum of all the masses

Example: Molar Mass Example: Find the molar mass for Ca. Br 2

Example: Molar Mass 1 Example: Find the molar mass for Ca. Br 2 Count the number of each type of atom Ca 1 Br 2

Example: Molar Mass 2 Example: Find the molar mass for Ca. Br 2 Find the molar mass of each atom on the periodic table Ca 1 40. 08 g/mole Br 2 79. 91 g/mole

Example: Molar Mass 3 Example: Find the molar mass for Ca. Br 2 Multiple the # of atoms molar mass for each atom Ca 1 40. 08 g/mole = 40. 08 g/mole Br 2 79. 91 g/mole = 159. 82 g/mole

Example: Molar Mass 4 Example: Find the molar mass for Ca. Br 2 Find the sum of all the masses Ca 1 40. 08 g/mole = 40. 08 g/mole Br 2 79. 91 g/mole = + 159. 82 g/mole 199. 90 g/mole 1 mole of Ca. Br 2 molecules would have a mass of 199. 90 g

Molar Mass A molar mass of a compound is the sum of the molar masses of the elements. Example: Water, H 2 O: 2 H = 2 x 1 g/mole = 2 g/mole 1 O = 1 x 16 g/mole = 16 g/mole molar mass of H 20 =18 g/mol
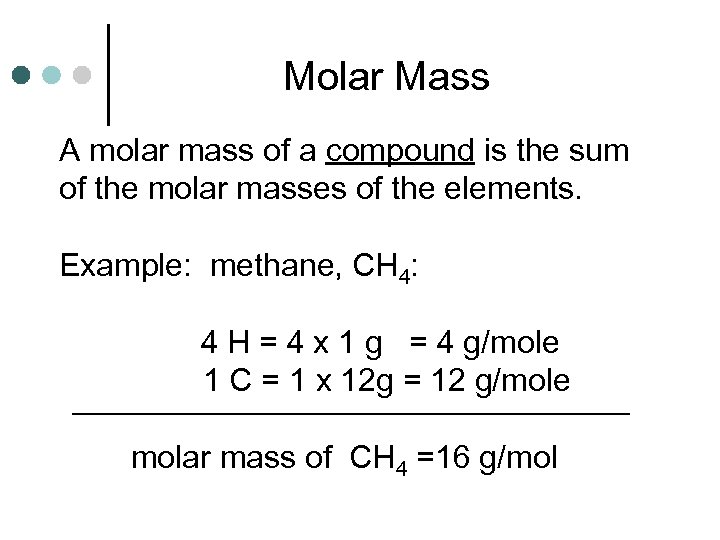
Molar Mass A molar mass of a compound is the sum of the molar masses of the elements. Example: methane, CH 4: 4 H = 4 x 1 g = 4 g/mole 1 C = 1 x 12 g = 12 g/mole molar mass of CH 4 =16 g/mol

Example: Molar Mass & Parenthesis Be sure to distribute the subscript outside the parenthesis to each element inside the parenthesis. Example: Find the molar mass for Sr(NO 3)2

Let’s Practice #1 Example: Find the molar mass for CH 2 Cl 2

Let’s Practice #2 Example: Find the molar mass for Al(OH)3

Classwork: C. 6: Molar Masses Page 163; questions 1 -9

Homework: C. 5 Supplement Worksheet Due:

C. 8: Molar Relationships

Molar mass for molecules The molar mass for a molecule = the sum of the molar masses of all the atoms in the molecule. Example: 1 mole of H 2 O = 18 grams 1 mole of H 2 O weighs 18 grams.

What happens when you do not have 18 grams of water? How do you calculate the number of moles of water?

Conversion Factors Conversion factor – a way that can be used to convert from one unit to the other. Example: the conversion between quarters and dollars: 4 quarters 1 dollar or 1 dollar 4 quarters

Conversion Factors Example: Determine the number of quarters in 12 dollars? (conversion factor) ? Quarters = 12 dollars x 4 quarters = 48 quarters 1 dollar

Conversion Factors Lets return to the term dozen. 12 roses = 1 dozen roses (conversion factor) 6 roses = ½ dozen Calculations: 6 roses____ 12 roses/dozen = 0. 5 dozen

Molar masses can be used as a conversion factor in chemical calculations. Molar masses allow the chemist to convert from grams to moles of a compound and from moles to grams of a compound. Grams molar mass Moles

Gram/Mole Conversions When converting between grams and moles, the molar mass is needed Example: The molar mass of helium is 4. 00 g/mol. To calculate how many grams of helium are in 2 moles of helium: amount of He in moles amount of He in grams 4. 00 g He 2. 00 mol He x 1 mol He = 8. 00 g He

Example: Moles to Grams Example: How many grams are in 1. 25 moles of water?

Example: Moles to Grams When converting between grams and moles, the molar mass is needed Example: How many grams are in 1. 25 moles of water? 1. 25 mol H 2 O H 2 1. 01 g/mole = 2. 02 g/mole O 1 16. 00 g/mole = + 16. 00 g/mole 18. 02 g/mole 1 mole H 2 O molecules = 18. 02 g H 2 O 1 mol H 2 O 22. 53 = _______ g H 2 O

Problem How many grams are in 2. 25 moles of iron, Fe?

Problem How many grams are in 2. 25 moles of iron, Fe? Answer: 126 grams Fe

Problem How many grams are in 0. 375 moles of potassium, K?

Problem How many grams are in 0. 375 moles of potassium, K? Answer: 14. 7 grams

Problem How many grams are in 20 moles of methane, CH 4?

Problem How many grams are in 20 moles of methane, CH 4? Answer: 320 grams

Grams to Moles If you are given a quantity in grams you can determine how moles you have by using the molar mass. Grams molar mass Moles

Let’s Practice Example: How many moles are in 25. 5 g Na. Cl?

Let’s Practice Na 1 22. 99 g/mole = 22. 99 g/mole Cl 1 35. 45 g/mole = + 35. 45 g/mole 58. 44 g/mole Example: How many moles are in 25. 5 g Na. Cl? 25. 5 g Na. Cl 1 mole Na. Cl molecules = 58. 44 g 1 mole Na. Cl 58. 44 g Na. Cl 0. 44 = _______ mole Na. Cl

Example: Grams to Moles A chemist produced 11. 9 g of aluminum, Al. How many moles of aluminum were produced? mass of Al in grams amount of Al in moles 1 mol Al 11. 9 g Al x 27 g Al = 0. 44 mol Al

Problem How many moles of calcium, Ca, are in 5. 00 grams of calcium?
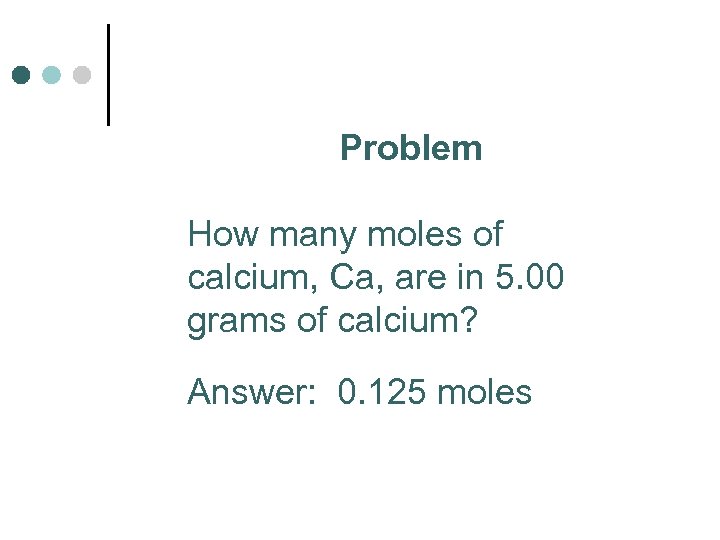
Problem How many moles of calcium, Ca, are in 5. 00 grams of calcium? Answer: 0. 125 moles

Problem How many moles of sodium chloride, Na. Cl, are in 75 grams of Na. Cl?

Problem How many moles of sodium chloride, Na. Cl, are in 75 grams of Na. Cl? Answer: 1. 28 moles

C. 8: Molar Relationships Classwork: C. 8 Problems Page 166 questions 1 -3 (hold on 4)

Homework: C. 7 -1 Supplement Worksheet Due:

C. 7: Equations and Molar Relationships How are chemical equations and molar masses related? 2 Cu. O 2 moles + C 2 Cu + CO 2 1 mole 2 moles 1 mole

C. 7: Equations and Molar Relationships 2 Cu. O 2 moles + C 1 mole 2 Cu + CO 2 2 moles 1 mole 159. 1 g + 12. 01 g 127. 1 g + 44 g 171. 1 g total Same total mass on the reactant and product side

C. 7: Equations and Molar Relationships Stoichiometry Power. Point

Example: Grams to Molecules Example: How many molecules are in 25. 5 g Na. Cl? Skip

Example: Grams to Molecules Example: How many molecules are in 25. 5 g Na. Cl? Na 1 22. 99 g/mole = 22. 99 g/mole Cl 1 35. 45 g/mole = + 35. 45 g/mole 58. 44 g/mole 1 moles Na. Cl molecules = 58. 44 g 1 mol = 6. 02 1023 molecules 25. 5 g Na. Cl 1 mol Na. Cl 58. 44 g Na. Cl 6. 02 1023 molecules Na. Cl 1 mol Na. Cl 2. 63 1023 = _____ molecules Na. Cl

Let’s Practice #4 Example: How many grams is a sample of 2. 75 × 1024 molecules of Sr. Cl 2? Skip

Homework: C. 7 -2 Supplement Worksheet Due:

C. 9: Percent Composition - The percent mass of each element found in a mixture

Mixtures Sample problem 1: A post-1982 penny with a mass of 2. 50 g is composed of 2. 44 g of zinc and 0. 06 g copper. What is the percent composition of each element?

The percent composition of the penny can be found by dividing the mass of each element by the total mass of the penny and multiplying by 100%. Zinc: 2. 44 g zinc 2. 50 g total Copper: x 100% = 97. 5% 0. 06 g Cu x 100% = 2. 5% 2. 50 g total Total percent must equal 100%

Relating molar mass and percent composition Sample problem 2: The formula for the copper containing mineral chalcocite is Cu 2 S. 1) What percentage of copper (Cu) is in this mineral? 2) What percentage of sulfur (S) is in this mineral?

The formula for chalcocite indicates one mole of Cu 2 S contains two molecules of Cu (127. 1 g) and one mole of S (32 g). The molar mass of Cu 2 S = 159. 2 g. % Cu = mass of Cu x 100% mass of Cu 2 S % Cu: 127. 1 g Cu x 100% = 79. 9% 159. 2 g Cu 2 S

The formula for chalcocite indicates one mole of Cu 2 S contains two molecules of Cu (127. 1 g) and one mole of S (32 g). The molar mass of Cu 2 S = 159. 2 g. % S = mass of S x 100% mass of Cu 2 S % Cu: 32 g Cu x 100% = 20. 1% 159. 2 g Cu 2 S

C. 10: Percent Composition Classwork: page 168, problems 2 and 4

C. 10: Percent Composition Homework: C. 10: Worksheet percent composition Due:

C. 11: Lab: Retrieving Copper Read over the lab procedure

C. 12: Conservation Renewable resources: resources that can be replenished. Examples include fresh water, air, fertile soil, plants and animals. As long as natural cycles are not disturbed too much, supplies of renewable resources can be maintained indefinitely.

Nonrenewable resources: resources that can not be readily replenished. Examples include metals, natural gas, coal and petroleum. The length of time to replenish these resources are very large.

End of Unit

Replacing: replace a resource by finding a substitute, preferably from renewable resources. Reusing: refurbish or repair an item to use again. Examples include car parts and printer cartridges. Recycle: reprocess to use again. Examples include aluminum cans, newspaper and glass bottles.

C. 12: Conservation C 12: Complete worksheet. These terms will appear again on a test or final exam!
cd471fa74a2065a7e4fbd69444973ade.ppt