53fa43f9113bda54afe11150a3be2c1c.ppt
- Количество слайдов: 25
 2. Attacks on Anonymized Social Networks
2. Attacks on Anonymized Social Networks
 2738&V Setting OE 9382 V 2783! • A social network • Edges may be private H#928! FGH 389 I 378 FG Y 5873 T 928&23 D 2893 L R 3579 X – E. g. , “communication graph” • The study of social structure by social networks – E. g. , the small world phenomenon – Requires data • Common practice – anonymization – “A rose by any other word would smell as sweet” – An anonymized network has same connectivity, clusterability , etc.
2738&V Setting OE 9382 V 2783! • A social network • Edges may be private H#928! FGH 389 I 378 FG Y 5873 T 928&23 D 2893 L R 3579 X – E. g. , “communication graph” • The study of social structure by social networks – E. g. , the small world phenomenon – Requires data • Common practice – anonymization – “A rose by any other word would smell as sweet” – An anonymized network has same connectivity, clusterability , etc.
 Main Contribution • Raising a privacy concern – Data is never released in the void • Proving the concern by presenting attacks ØOne cannot rely on anonymization • Thus, highlighting the need for mathematical rigor – (But isn’t DP + calibrated noise mechanism rigorous enough? ) DB
Main Contribution • Raising a privacy concern – Data is never released in the void • Proving the concern by presenting attacks ØOne cannot rely on anonymization • Thus, highlighting the need for mathematical rigor – (But isn’t DP + calibrated noise mechanism rigorous enough? ) DB
 Key Idea • Goal: Given a single anonymized network, deanonymize 2 nodes and learn if connected • What is the challenge? – Compare to breaking anonymity of Netflix • What special kind of auxiliary data can be used? – Hint: Active attacks in Cryptography • Solution – “Steganography”
Key Idea • Goal: Given a single anonymized network, deanonymize 2 nodes and learn if connected • What is the challenge? – Compare to breaking anonymity of Netflix • What special kind of auxiliary data can be used? – Hint: Active attacks in Cryptography • Solution – “Steganography”
 Outline • Attacks on anonymized networks – high level description • The “Walk-Based” active attack – Description – Analysis – Experiments • Passive attack
Outline • Attacks on anonymized networks – high level description • The “Walk-Based” active attack – Description – Analysis – Experiments • Passive attack
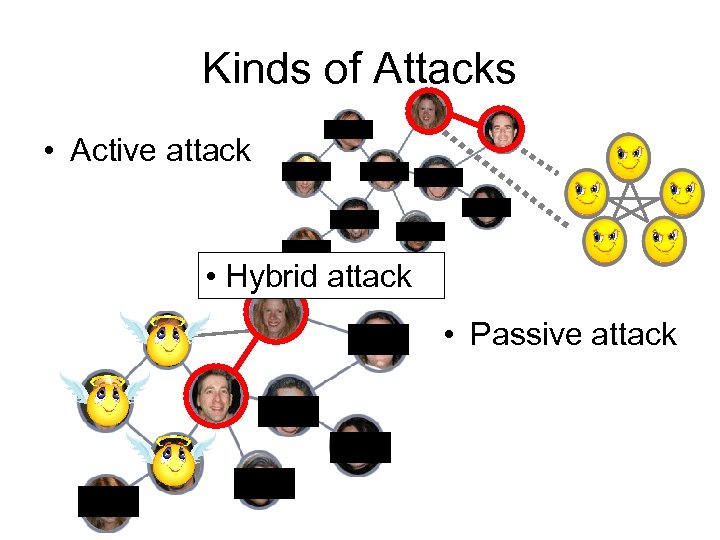 Kinds of Attacks • Active attack • Hybrid attack • Passive attack
Kinds of Attacks • Active attack • Hybrid attack • Passive attack
 Active Attacks - Challenges Let G be the network, H the subgraph With high probability, H must be: • Uniquely identifiable in G – For any G • Efficiently locatable – Tractable instance of subgraph isomorphism • But undetectable – From the point of view of the data curator
Active Attacks - Challenges Let G be the network, H the subgraph With high probability, H must be: • Uniquely identifiable in G – For any G • Efficiently locatable – Tractable instance of subgraph isomorphism • But undetectable – From the point of view of the data curator
 Active Attacks - Approaches • Basic idea: H is randomly generated – Start with k nodes, add edges independently at random The “Walk-based” attack • Two variants: – better in practice – k = Θ(logn) de-anonymizes Θ(log 2 n) users – k = Θ(√logn) de-anonymizes Θ(√ logn) users • • H needs to be “more unique” Achieved by “thin” attachment of H to G The “Cut-based” attack – matches theoretical bound
Active Attacks - Approaches • Basic idea: H is randomly generated – Start with k nodes, add edges independently at random The “Walk-based” attack • Two variants: – better in practice – k = Θ(logn) de-anonymizes Θ(log 2 n) users – k = Θ(√logn) de-anonymizes Θ(√ logn) users • • H needs to be “more unique” Achieved by “thin” attachment of H to G The “Cut-based” attack – matches theoretical bound
 Outline • Attacks on anonymized networks – high level description • The Walk-Based active attack – Description – Analysis – Experiments • Passive attack
Outline • Attacks on anonymized networks – high level description • The Walk-Based active attack – Description – Analysis – Experiments • Passive attack
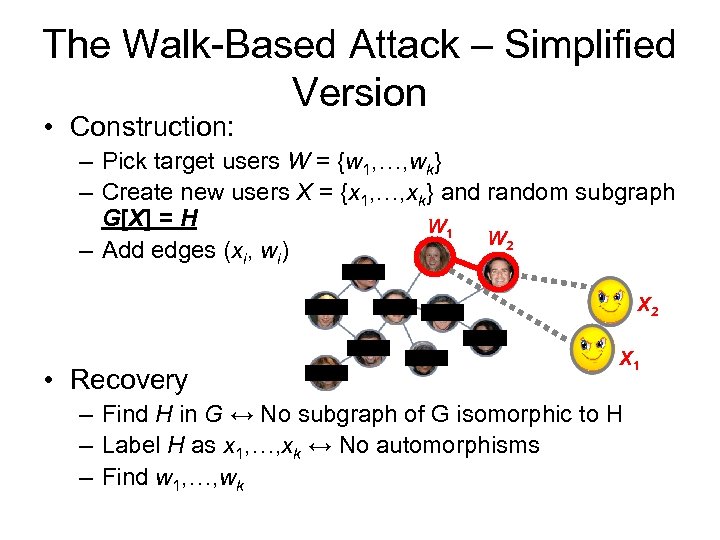 The Walk-Based Attack – Simplified Version • Construction: – Pick target users W = {w 1, …, wk} – Create new users X = {x 1, …, xk} and random subgraph G[X] = H W 1 W 2 – Add edges (xi, wi) X 2 • Recovery X 1 – Find H in G ↔ No subgraph of G isomorphic to H – Label H as x 1, …, xk ↔ No automorphisms – Find w 1, …, wk
The Walk-Based Attack – Simplified Version • Construction: – Pick target users W = {w 1, …, wk} – Create new users X = {x 1, …, xk} and random subgraph G[X] = H W 1 W 2 – Add edges (xi, wi) X 2 • Recovery X 1 – Find H in G ↔ No subgraph of G isomorphic to H – Label H as x 1, …, xk ↔ No automorphisms – Find w 1, …, wk
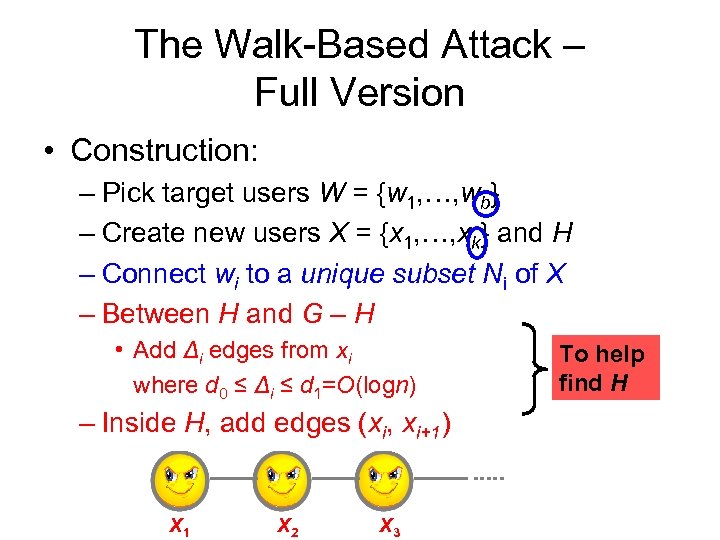 The Walk-Based Attack – Full Version • Construction: – Pick target users W = {w 1, …, wb} – Create new users X = {x 1, …, xk} and H – Connect wi to a unique subset Ni of X – Between H and G – H • Add Δi edges from xi where d 0 ≤ Δi ≤ d 1=O(logn) – Inside H, add edges (xi, xi+1) X 1 X 2 X 3 To help find H
The Walk-Based Attack – Full Version • Construction: – Pick target users W = {w 1, …, wb} – Create new users X = {x 1, …, xk} and H – Connect wi to a unique subset Ni of X – Between H and G – H • Add Δi edges from xi where d 0 ≤ Δi ≤ d 1=O(logn) – Inside H, add edges (xi, xi+1) X 1 X 2 X 3 To help find H
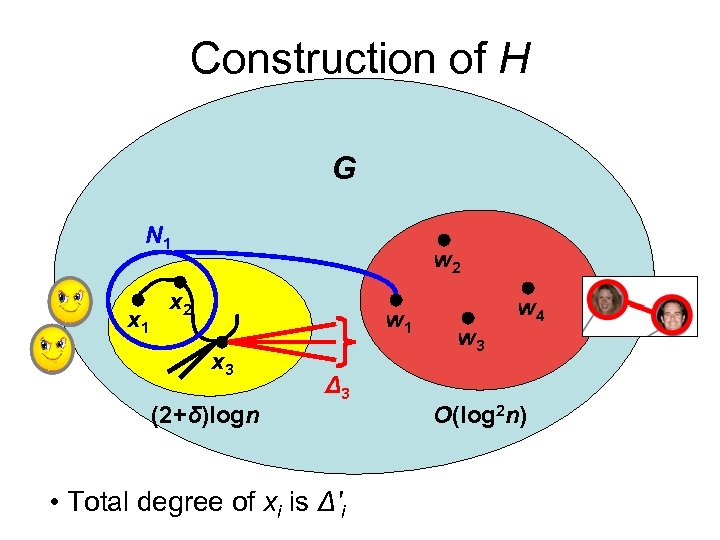 Construction of H G N 1 x 1 w 2 x 2 w 1 x 3 (2+δ)logn Δ 3 • Total degree of xi is Δ'i w 3 w 4 O(log 2 n)
Construction of H G N 1 x 1 w 2 x 2 w 1 x 3 (2+δ)logn Δ 3 • Total degree of xi is Δ'i w 3 w 4 O(log 2 n)
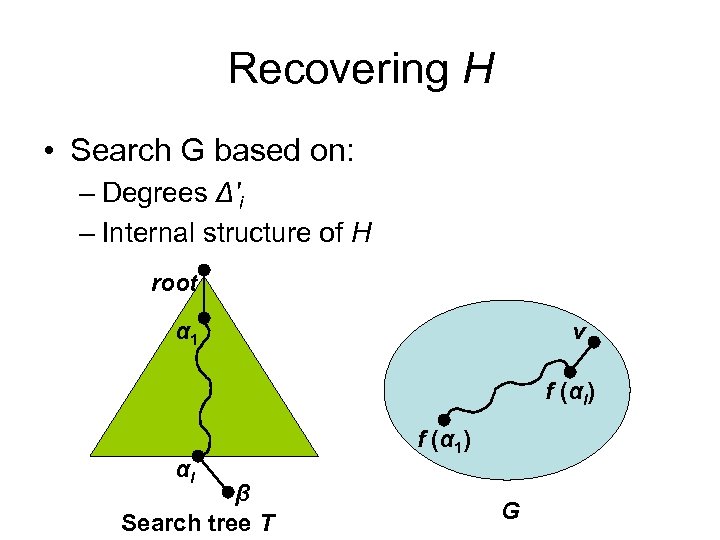 Recovering H • Search G based on: – Degrees Δ'i – Internal structure of H root α 1 v f (αl) αl β Search tree T f (α 1) G
Recovering H • Search G based on: – Degrees Δ'i – Internal structure of H root α 1 v f (αl) αl β Search tree T f (α 1) G
![Analysis • Theorem 1 [Correctness]: With high probability, H is unique in G. Formally: Analysis • Theorem 1 [Correctness]: With high probability, H is unique in G. Formally:](https://present5.com/presentation/53fa43f9113bda54afe11150a3be2c1c/image-14.jpg) Analysis • Theorem 1 [Correctness]: With high probability, H is unique in G. Formally: – H is a random subgraph – G is arbitrary – Edges between H and G – H are arbitrary – There are edges (xi, xi+1) Ø Then WHP no subgraph of G is isomorphic to H. • Theorem 2 [Efficiency]: Search tree T does not grow too large. Formally: – For every ε, WHP the size of T is O(n 1+ε)
Analysis • Theorem 1 [Correctness]: With high probability, H is unique in G. Formally: – H is a random subgraph – G is arbitrary – Edges between H and G – H are arbitrary – There are edges (xi, xi+1) Ø Then WHP no subgraph of G is isomorphic to H. • Theorem 2 [Efficiency]: Search tree T does not grow too large. Formally: – For every ε, WHP the size of T is O(n 1+ε)
![Theorem 1 [Correctness] • H is unique in G. Two cases: – For no Theorem 1 [Correctness] • H is unique in G. Two cases: – For no](https://present5.com/presentation/53fa43f9113bda54afe11150a3be2c1c/image-15.jpg) Theorem 1 [Correctness] • H is unique in G. Two cases: – For no disjoint subset S, G[S] isomorphic to H – For no overlapping S, G[S] isomorphic to H • Case 1: – S =
Theorem 1 [Correctness] • H is unique in G. Two cases: – For no disjoint subset S, G[S] isomorphic to H – For no overlapping S, G[S] isomorphic to H • Case 1: – S = nodes in G – H – εS – the event that si ↔ xi is an isomorphism – – By Union Bound,
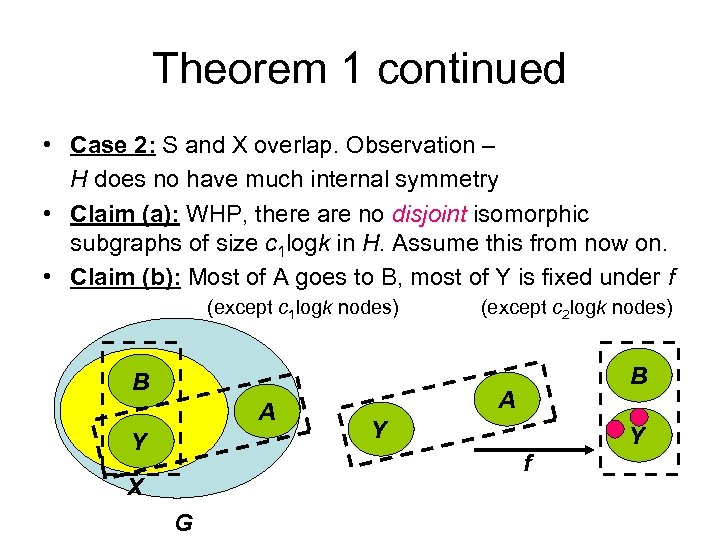 Theorem 1 continued • Case 2: S and X overlap. Observation – H does no have much internal symmetry • Claim (a): WHP, there are no disjoint isomorphic subgraphs of size c 1 logk in H. Assume this from now on. • Claim (b): Most of A goes to B, most of Y is fixed under f (except c 1 logk nodes) B A Y (except c 2 logk nodes) B A Y Y f X G
Theorem 1 continued • Case 2: S and X overlap. Observation – H does no have much internal symmetry • Claim (a): WHP, there are no disjoint isomorphic subgraphs of size c 1 logk in H. Assume this from now on. • Claim (b): Most of A goes to B, most of Y is fixed under f (except c 1 logk nodes) B A Y (except c 2 logk nodes) B A Y Y f X G
 Theorem 1 - Proof • What is the probability of an overlapping second copy of H in G? • f. ABCD : AUY → BUY = X B C • Let j = |A| = |B| = |C| D A • εABCD – the event that f. ABCD is Y' an isomorphism • #random edges inside C ≥ j(j-1)/2 – (j-1) X • #random edges between C and Y' ≥ (|Y'|)j – 2 j • Probability that the random edges match those of A Pr[εABCD] ≤ 2#random edges A D B, C
Theorem 1 - Proof • What is the probability of an overlapping second copy of H in G? • f. ABCD : AUY → BUY = X B C • Let j = |A| = |B| = |C| D A • εABCD – the event that f. ABCD is Y' an isomorphism • #random edges inside C ≥ j(j-1)/2 – (j-1) X • #random edges between C and Y' ≥ (|Y'|)j – 2 j • Probability that the random edges match those of A Pr[εABCD] ≤ 2#random edges A D B, C
![Theorem 2 [Efficiency] • Claim: Size of search tree T is near-linear. • Proof Theorem 2 [Efficiency] • Claim: Size of search tree T is near-linear. • Proof](https://present5.com/presentation/53fa43f9113bda54afe11150a3be2c1c/image-18.jpg) Theorem 2 [Efficiency] • Claim: Size of search tree T is near-linear. • Proof uses similar methods: – Define random variables: • #nodes in T = Γ • Γ = Γ' + Γ'' = #paths in G – H + #paths passing in H – This time we bound E(Γ') [and similarly E(Γ'')] – Number of paths of length j with max degree d 1 is bounded – Probability of such a path to have correct internal structure is bounded Ø E(Γ') ≤ (#paths * Pr[correct internal struct])
Theorem 2 [Efficiency] • Claim: Size of search tree T is near-linear. • Proof uses similar methods: – Define random variables: • #nodes in T = Γ • Γ = Γ' + Γ'' = #paths in G – H + #paths passing in H – This time we bound E(Γ') [and similarly E(Γ'')] – Number of paths of length j with max degree d 1 is bounded – Probability of such a path to have correct internal structure is bounded Ø E(Γ') ≤ (#paths * Pr[correct internal struct])
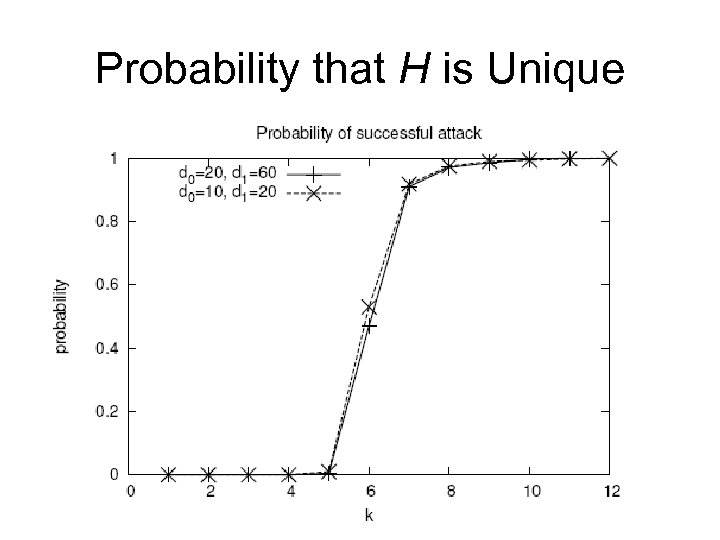
 Experiments • Data: Network of friends on Live. Journal – 4. 4∙ 106 nodes, 77∙ 106 edges • Uniqueness: With 7 nodes, an average of 70 nodes can be de-anonymized – Although log(4. 4∙ 106) ≈ 15 • Efficiency: |T| is typically ~9∙ 104 • Detectability: – Only 7 nodes – Many subgraphs of 7 nodes in G are dense and well-connected
Experiments • Data: Network of friends on Live. Journal – 4. 4∙ 106 nodes, 77∙ 106 edges • Uniqueness: With 7 nodes, an average of 70 nodes can be de-anonymized – Although log(4. 4∙ 106) ≈ 15 • Efficiency: |T| is typically ~9∙ 104 • Detectability: – Only 7 nodes – Many subgraphs of 7 nodes in G are dense and well-connected
 Probability that H is Unique
Probability that H is Unique
 Outline • Attacks on anonymized networks – high level description • The Walk-Based active attack – Description – Analysis – Experiments • Passive attack
Outline • Attacks on anonymized networks – high level description • The Walk-Based active attack – Description – Analysis – Experiments • Passive attack
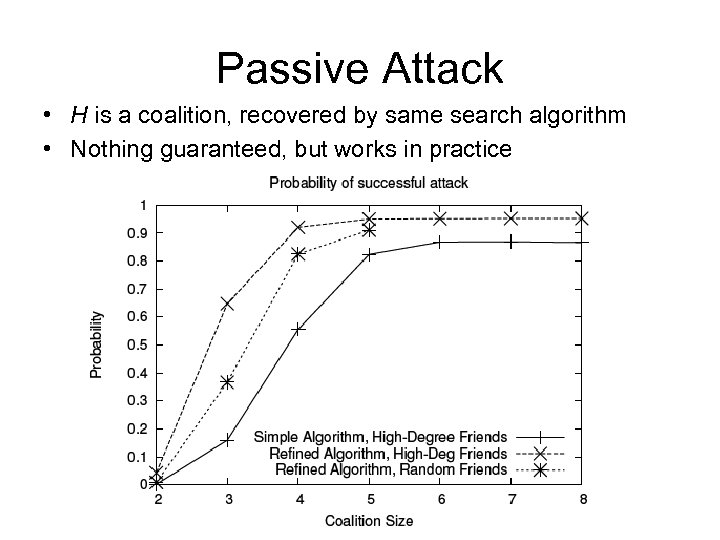 Passive Attack • H is a coalition, recovered by same search algorithm • Nothing guaranteed, but works in practice
Passive Attack • H is a coalition, recovered by same search algorithm • Nothing guaranteed, but works in practice
 Summary & Open Questions • One cannot rely on anonymization of social networks • Major open problem – what (if anything) can be done in the non-interactive model? – Released object must answer many questions accurately while preserving privacy – Noise must increase with number of questions [DN 03] • Novel models
Summary & Open Questions • One cannot rely on anonymization of social networks • Major open problem – what (if anything) can be done in the non-interactive model? – Released object must answer many questions accurately while preserving privacy – Noise must increase with number of questions [DN 03] • Novel models
 Any Questions? • Thank you
Any Questions? • Thank you
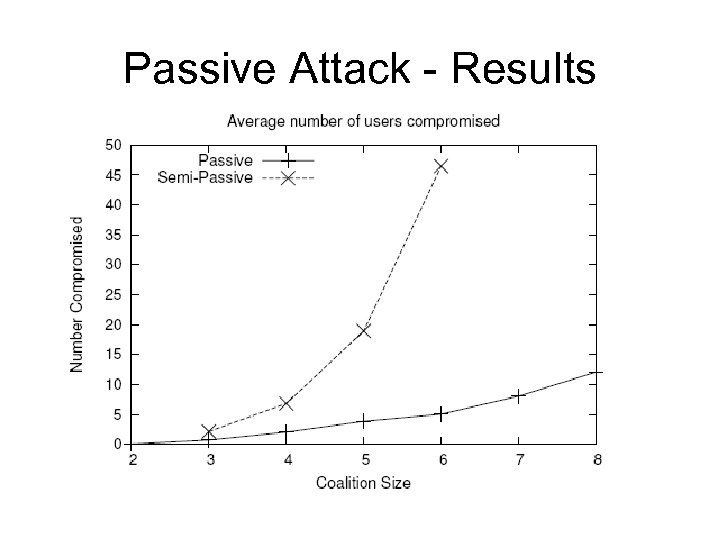 Passive Attack - Results
Passive Attack - Results


