2 5 2018 Тема 5 Введение в логику Платон

2/5/2018 Тема № 5. Введение в логику «Платон мне друг, но истина дороже» Аристотель «Платон и Аристотель» Рафаэль Санти МБОУ г. Иркутска лицей ИГУ, ligu. edu 38. ru Лавлинский М. В. , Lavlinski. MV@mail. ru

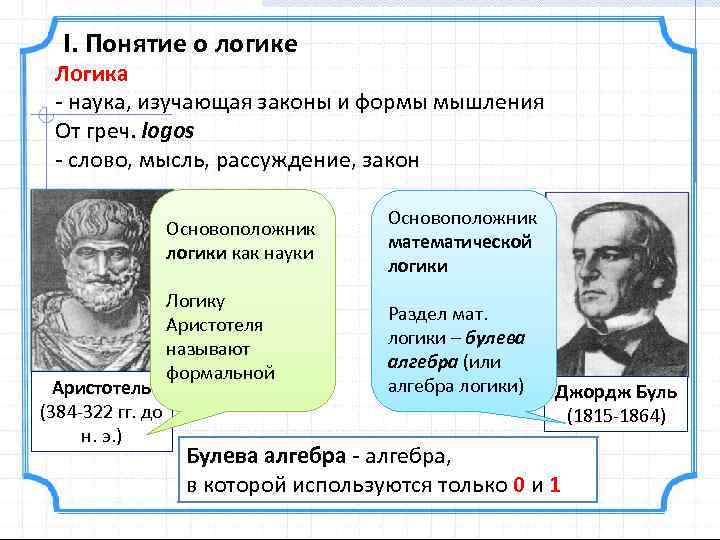I. Понятие о логике Логика - наука, изучающая законы и формы мышления От греч. logos - слово, мысль, рассуждение, закон Основоположник логики как науки Аристотель (384 -322 гг. до н. э. ) Логику Аристотеля называют формальной Основоположник математической логики Раздел мат. логики – булева алгебра (или алгебра логики) Джордж Буль (1815 -1864) Булева алгебра - алгебра, в которой используются только 0 и 1

II. Логическое высказывание – повествовательное предложение, относительно которого можно сказать, истинно оно или ложно. Высказывание или нет? q Сейчас идет дождь. q Жирафы летят на север. q История – интересный предмет. q У квадрата – 10 сторон и все разные. q Красиво! q В городе N живут 2 миллиона человек. q Который час?

Обозначение высказываний простые высказывания A – Сейчас идет дождь. (элементарные) B – Форточка открыта. ! высказывание ложно (0) или истинно (1) Составные высказывания строятся из простых с помощью логических связок (операций): «и» , «или» , «не» , «если … то» , «тогда и только тогда» Aи. B A или не B если A, то B не A и B A тогда и только тогда, когда B Сейчас идет дождь и открыта форточка. Сейчас идет дождь или форточка закрыта. Если сейчас идет дождь, то форточка открыта. Сейчас нет дождя и форточка открыта. Дождь идет тогда и только тогда, когда открыта форточка.

III. Логические операции

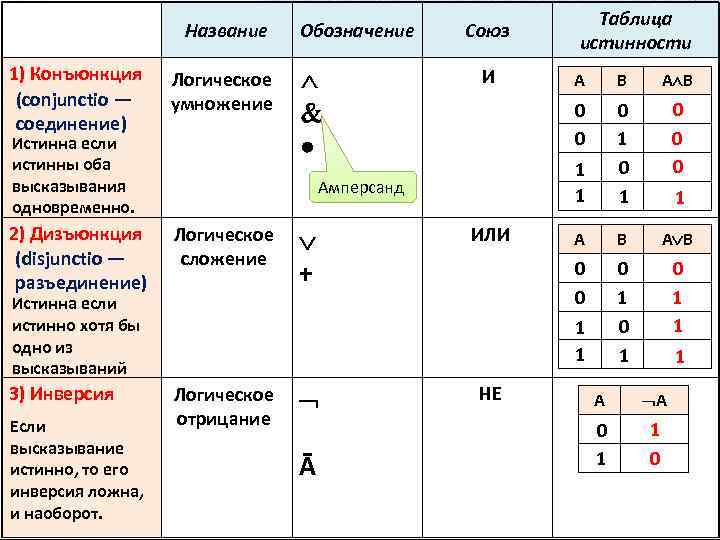Название 1) Конъюнкция (conjunctio — соединение) Логическое умножение Истинна если истинны оба высказывания одновременно. 2) Дизъюнкция (disjunctio — разъединение) Обозначение Союз И + 3) Инверсия Если высказывание истинно, то его инверсия ложна, и наоборот. А В 0 1 0 0 0 А В 0 0 Истинна если истинно хотя бы одно из высказываний В 1 1 ИЛИ А 0 0 Амперсанд Логическое сложение Таблица истинности 0 1 0 1 1 Логическое отрицание Ā НЕ 1 1 А А 0 1 1 0

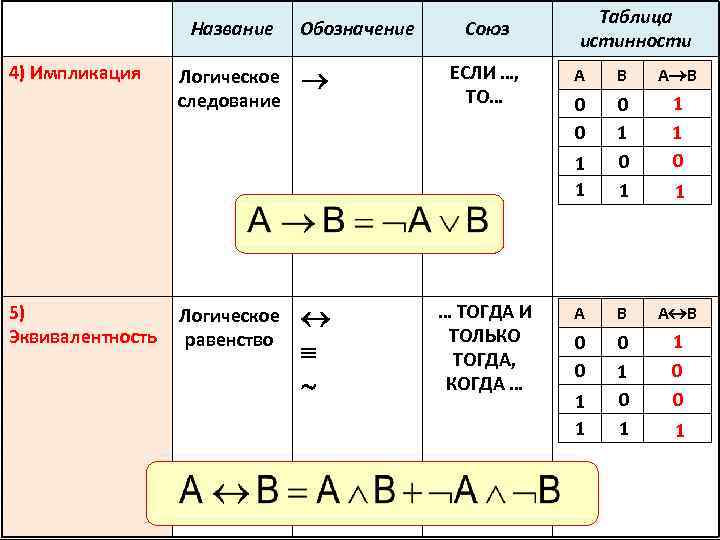Название 4) Импликация Обозначение Союз ЕСЛИ …, ТО… Таблица истинности 5) Эквивалентность Логическое равенство … ТОГДА И ТОЛЬКО ТОГДА, КОГДА … А В 0 0 1 1 Логическое следование 0 1 1 1 0 А В 0 0 0 1 1

IV. Логические выражения (ЛВ) 1) Простые высказывания обозначены буквами (переменными) 2) Использованы логические операции #1. Система сигнализации должна дать аварийный сигнал, если вышли из строя два из трех двигателей самолета. Обозначим высказывания: А — “ 1 -ый двигатель вышел из строя”. B — “ 2 -ой двигатель вышел из строя”. C — “ 3 -ий двигатель вышел из строя”. X — “Аварийная ситуация”. Мы выполнили X= формализацию (A B) (A C) (B C) Формализация — это переход от конкретного содержания к формальной записи с помощью некоторого языка.

Порядок выполнения операций в ЛВ 1) ( ) 2) 3) 4) 5) 6)

#2. Найдите значения логических выражений F = (0 v 0) v (1 v 1) 1 F = (1 v 1) v (1 v 0) 1 F = (0 & 0) & (1 & 0) 0 F = ¬ 1 & (1 v 1) v (¬ 0 & 1) 1 F = (¬ 1 v 1) & (1 &¬ 1) &(¬ 1 V 0) 0

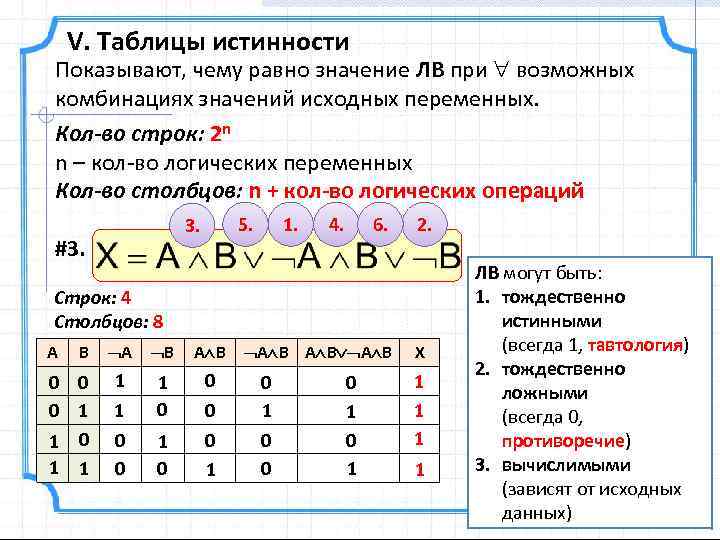V. Таблицы истинности Показывают, чему равно значение ЛВ при возможных комбинациях значений исходных переменных. Кол-во строк: 2 n n – кол-во логических переменных Кол-во столбцов: n + кол-во логических операций #3. 1. 5. 3. 6. 4. 2. Cтрок: 4 Столбцов: 8 А В 0 0 0 1 1 А В А В 1 1 0 0 0 1 А В А В 0 1 0 0 0 1 X 1 1 ЛВ могут быть: 1. тождественно истинными (всегда 1, тавтология) 2. тождественно ложными (всегда 0, противоречие) 3. вычислимыми (зависят от исходных данных)

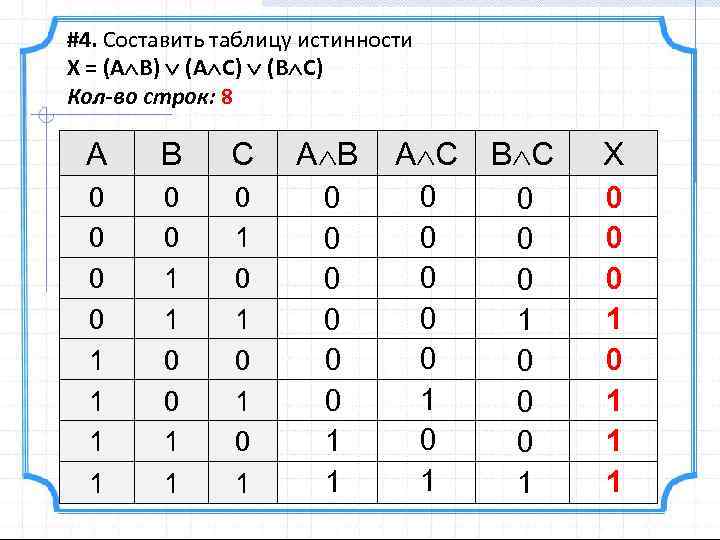#4. Составить таблицу истинности X = (A B) (A C) (B C) Кол-во строк: 8 A B C A B A C B C X 0 0 1 1 0 1 0 1 0 0 0 1 0 0 0 1 1 1

VI. Решение задач Задача 1. Каково наибольшее целое число X, при котором истинно высказывание С =(90 < X 2)→(80>(X + 2)2) Решение: 1) Заменим импликацию A→B = A B 6 9 -10 -9 2) A = (90 < X 2 )= 90 ≥ X 2 3) С = (90 ≥ X 2) (80>(X + 2)2) 4) Х Z (90 ≥ X 2) (− 9 ≤ X ≤ 9) 5) 80>(X + 2)2 8 ≥ |X + 2| -10 ≤ X ≤ 6 Ответ: 9 6) С = (− 9 ≤ X ≤ 9) (-10 ≤ X ≤ 6)

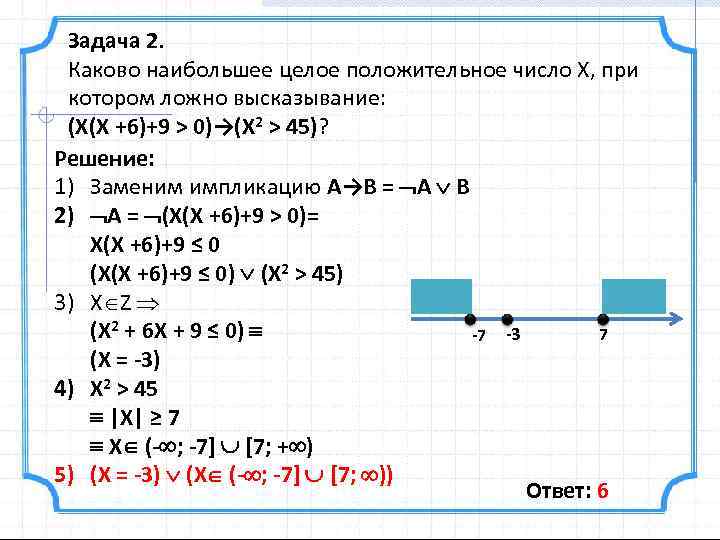Задача 2. Каково наибольшее целое положительное число X, при котором ложно высказывание: (X(X +6)+9 > 0)→(X 2 > 45)? Решение: 1) Заменим импликацию A→B = A B 2) A = (X(X +6)+9 > 0)= X(X +6)+9 ≤ 0 (X(X +6)+9 ≤ 0) (X 2 > 45) 3) Х Z (X 2 + 6 Х + 9 ≤ 0) 7 -7 -3 (X = -3) 4) X 2 > 45 |X| ≥ 7 Х (- ; -7] [7; + ) 5) (X = -3) (Х (- ; -7] [7; )) Ответ: 6

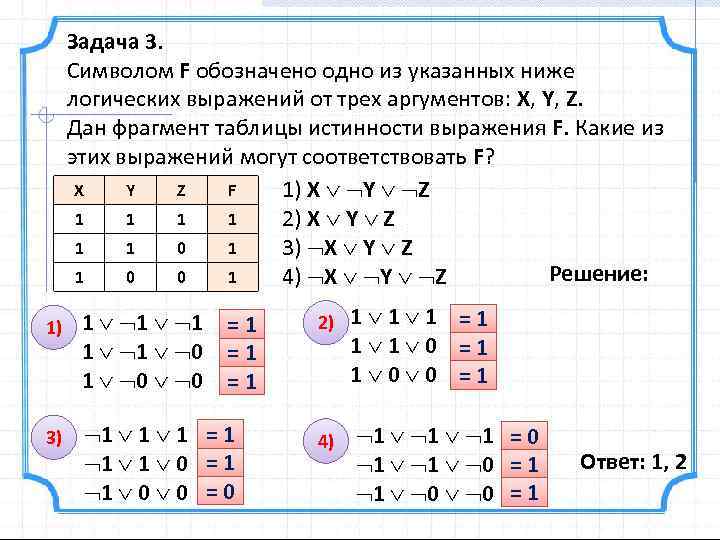Задача 3. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F. Какие из этих выражений могут соответствовать F? X Y Z F 1) X Y Z 1 1 2) X Y Z 1 1 0 1 3) X Y Z Решение: 1 0 0 1 4) X Y Z 1) 1 1 1 0 0 3) 1 1 1 = 1 1 1 0 = 1 1 0 0 =1 =1 =1 2) 4) 1 1 1 =1 1 1 0 =1 1 0 0 =1 1 1 1 = 0 1 1 0 = 1 1 0 0 = 1 Ответ: 1, 2

Задача 4. Определите значение логического выражения (X > 2) → (X > 3) для X = 1, 2, 3, 4. Решение: 1) X = 1 (1 > 2) → (1 > 3) 0→ 0 1 3) X = 3 (3 > 2) → (3 > 3) 1→ 0 0 2) X = 2 (2 > 2) → (2 > 3) 0→ 0 1 4) X = 4. (4 > 2) → (4 > 3) 1→ 1 1 Ответ: 1, 1, 0, 1

Задача 5. Для какого имени истинно высказывание: ¬ (Первая буква имени гласная → Четвертая буква имени согласная)? 1) ЕЛЕНА 2) ВАДИМ 3) АНТОН 4) ФЕДОР Решение: 1) ¬ (Первая буква имени гласная → Четвертая буква имени согласная) 1 2) Первая буква имени гласная → Четвертая буква имени согласная 0 3) Первая буква имени гласная 1 Четвертая буква имени согласная 0 Ответ: 3

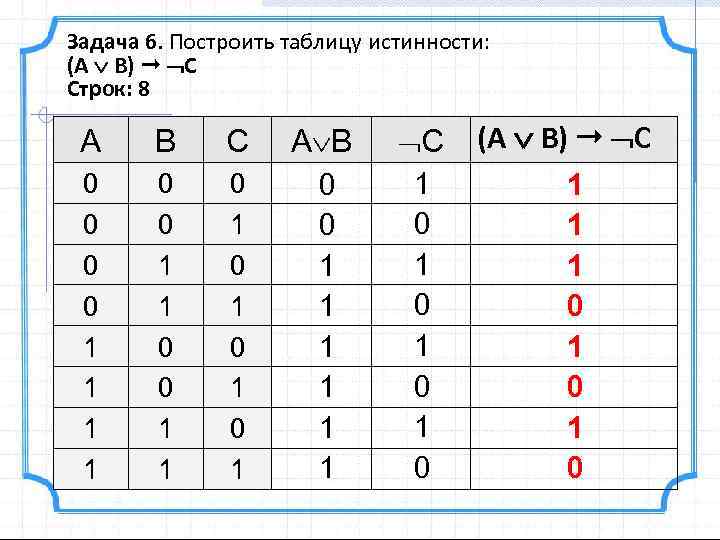Задача 6. Построить таблицу истинности: (A B) C Строк: 8 A B C A B C 0 0 1 1 0 1 0 1 0 0 1 1 1 1 0 1 0 (A B) C 1 1 1 0 1 0

Задача 7. Каково наибольшее целое положительное число X, при котором ложно высказывание: (7 X – 3 < 75)→(X(X-1)>65) Решение: 1) Заменим импликацию A→B = A B 2) A = (7 X – 3 < 75)= 7 X – 3 ≥ 75 (7 X – 3 ≥ 75) (X(X-1)>65) 3) Х Z (7 X – 3 ≥ 75) (X ≥ 78/7) -9 9 12 (X ≥ 12) • X(X-1)>65 X 2 - X- 65 > 0 Х (- ; -9] [9; + ) 1) (X ≥ 12) (Х (- ; -9] [9; + )) Ответ: 8

Дискретная математика, 9 класс 2/5/2018 Домашнее задание 1. Конспект 2. СР 3. [ДЗ-1] Введение в логику. doc МБОУ г. Иркутска лицей ИГУ, ligu. edu 38. ru