* 2 3 * * 6 7 * Магичес ки е * * * * * квадраты * * * 8 * * 58 * 5 4 * * 62 63 1
Автор: Циуля Никита, учащийся 5 класса ГУО «Грицкевичская средняя школа» Руководитель: Данилова Елена Ивановна, учитель математики и информатики
Магическим квадратом n-го порядка называется квадратная таблица размером n х n, заполненная натуральными числами от 1 до n 2, суммы которых по всем строкам, столбцам и обеим диагоналям одинаковы. Различают магические квадраты четного и нечетного порядка (в зависимости oт четности n). Поля таблицы, в которые записывают числа, называются клетками магического квадрата, а сумма чисел, стоящих в любой строке, столбце или на диагонали, – его постоянной.
Тема исследования: • Составление магических квадратов Объект исследования: Магический квадрат
Цель исследования: • Раскрыть «секреты» магических квадратов и изучить области их применения Задачи исследования: • познакомиться с историей появления магических квадратов; • выяснить виды магических квадратов и способы их заполнения; • узнать, многие ли ученики нашей школы знакомы с чудесными квадратами и умеют ли их заполнять; • выявить области применения магических квадратов.
Актуальность: В сборниках нестандартных задач по математике часто встречаются задачи на составление магических квадратов. Кроме того, такие задания нередко включают в математические олимпиады, поэтому ребятам, увлекающимся математикой, полезно знать способы решения задач такого типа.
Методы исследования: поисковый метод с использованием метод математического расчета; научной и учебной литературы, поиск необходимой информации в экспериментальный метод; анализ полученных в ходе сети Интернет; исследования данных практический метод составления магических квадратов на основе полученных знаний;
История возникновения магических квадратов Возникновение магических квадратов относится к глубокой древности. «Придуманы магические квадраты впервые, по-видимому, китайцами, так как самое раннее упоминание о них встречается в китайской книге, написанной за 4000 - 5000 лет до нашей эры» (Б. А. Кордемский, «Математическая смекалка» ).
История возникновения магических квадратов • Согласно легенде, во времена правления императора Ю (около 2200 лет до н. э. ) из вод Хуанхэ (Желтой реки) всплыла священная черепаха, на панцире которой были начертаны таинственные иероглифы, и эти знаки известны под названием Ло-Шу. Река Хуанхэ Квадрат Ло-Шу Священная черепаха
История возникновения магических квадратов • Таблица Ло-Шу состоит из 9 клеток: 3 строк и 3 столбцов, заполненных натуральными числами от 1 до 9. В этом магическом квадрате суммы чисел по всем строкам, столбцам и двум диагоналям равны одному и тому же числу 15. • Более поздние сведения о магических квадратах, относящиеся уже к I веку, получены из Индии.
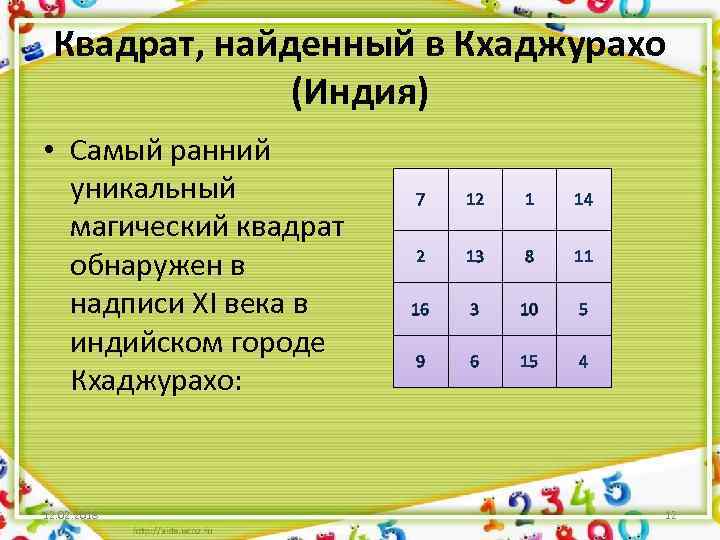Квадрат, найденный в Кхаджурахо (Индия) • Самый ранний уникальный магический квадрат обнаружен в надписи XI века в индийском городе Кхаджурахо: 12. 02. 2018 7 12 1 14 2 13 8 11 16 3 10 5 9 6 15 4 12
История возникновения магических квадратов • Из Индии сведения о магических квадратах перешли к арабам. В Европе о магических квадратах узнали благодаря византийскому писателю Э. Мосхопулосу, жившему в Константинополе в начале XV века. • А в начале XVI века один из магических квадратов был увековечен выдающимся немецким художником, гравёром и немного математиком Альбрехтом Дюрером в его лучшей гравюре «Меланхолия» (1514 г. )
История возникновения магических квадратов Альбрехт Дюрер (1471 – 1528) Гравюра на меди «Меланхолия» , 1514 год
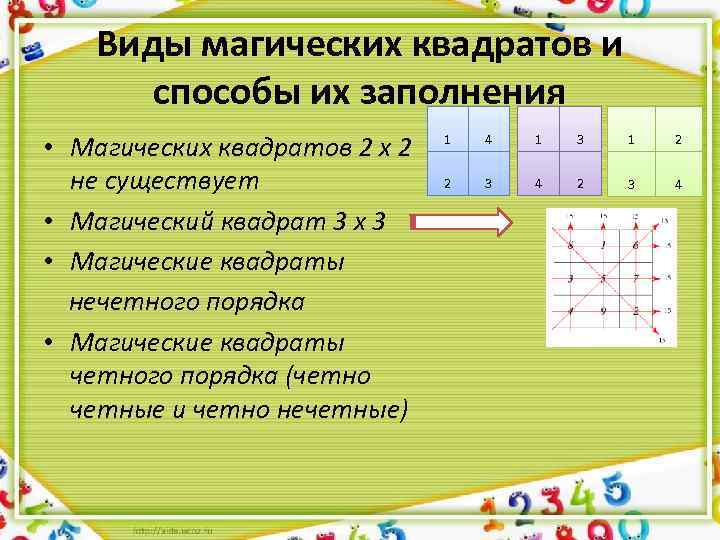Виды магических квадратов и способы их заполнения • Магических квадратов 2 х 2 не существует • Магический квадрат 3 х 3 • Магические квадраты нечетного порядка • Магические квадраты четного порядка (четно четные и четно нечетные) 1 4 1 3 1 2 2 3 4
Виды магических квадратов и способы их заполнения C увеличением размеров (числа клеток) квадрата быстро растет количество возможных магических квадратов. Так, например, различных магических квадратов 4 х4 уже 880. Французский академик Бернар Френикль де Бесси в «Общей таблице магических квадратов в четыре» привёл все 880 магических квадратов четвёртого порядка. Таблица занимает 43 страницы книги. Трудно представить себе, сколько времени заняла у Френикля эта работа.
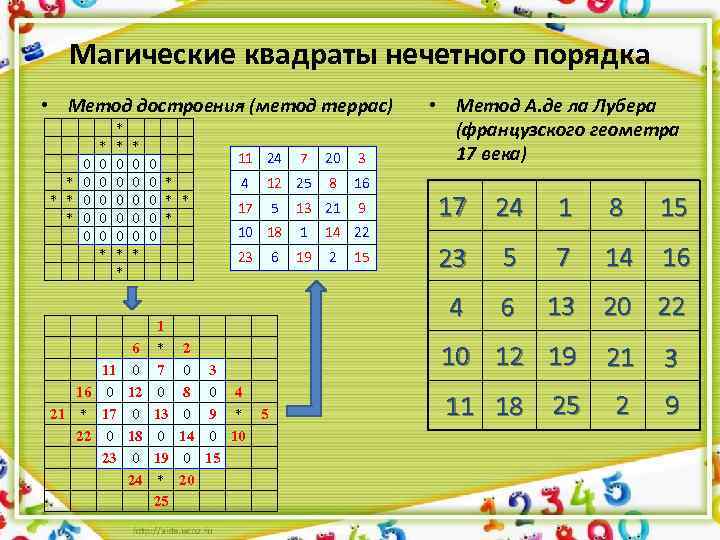Магические квадраты нечетного порядка • Метод достроения (метод террас) 0 * * 0 0 0 0 0 * * 11 16 0 21 * 17 22 0 23 * 0 0 0 * 6 0 12 0 18 0 24 0 0 * * 0 11 24 7 20 3 4 12 25 8 16 17 5 13 21 9 1 14 22 23 1 * 7 0 13 0 19 * 25 10 18 19 2 6 15 • Метод А. де ла Лубера (французского геометра 17 века) 17 24 1 8 15 16 23 5 7 14 22 4 6 13 20 6 13 2 0 8 0 14 0 20 3 0 4 9 * 5 0 10 15 10 12 19 21 3 11 25 2 9 18
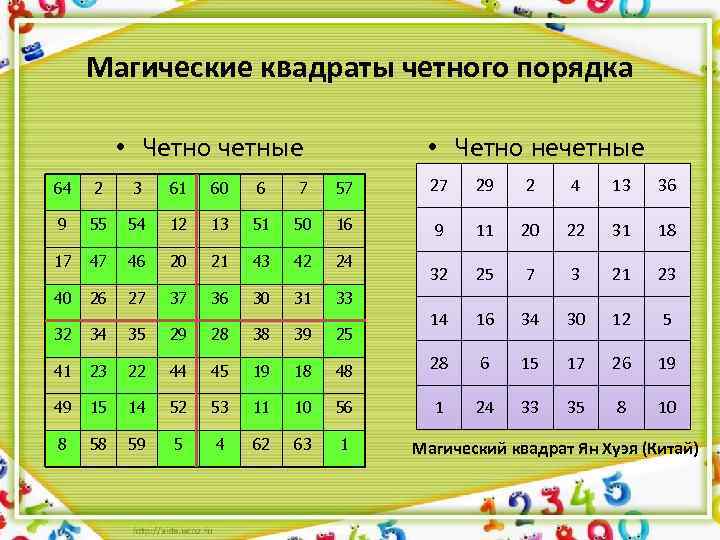Магические квадраты четного порядка • Четно четные • Четно нечетные 64 2 3 61 60 6 7 57 27 29 2 4 13 36 9 55 54 12 13 51 50 16 9 11 20 22 31 18 17 47 46 20 21 43 42 24 32 25 7 3 21 23 40 26 27 37 36 30 31 33 14 16 34 30 12 5 32 34 35 29 28 38 39 25 41 23 22 44 45 19 18 48 28 6 15 17 26 19 49 15 14 52 53 11 10 56 1 24 33 35 8 10 8 58 59 5 4 62 63 1 Магический квадрат Ян Хуэя (Китай)
Но можно и самому сделать магический квадрат. Вот магический квадрат 4 х4, который я сделал сам: 1 12 8 13 15 6 10 3 14 7 11 2 4 9 5 16 Попробуйте сами сделать магический квадрат. Если постараетесь, обязательно получится.
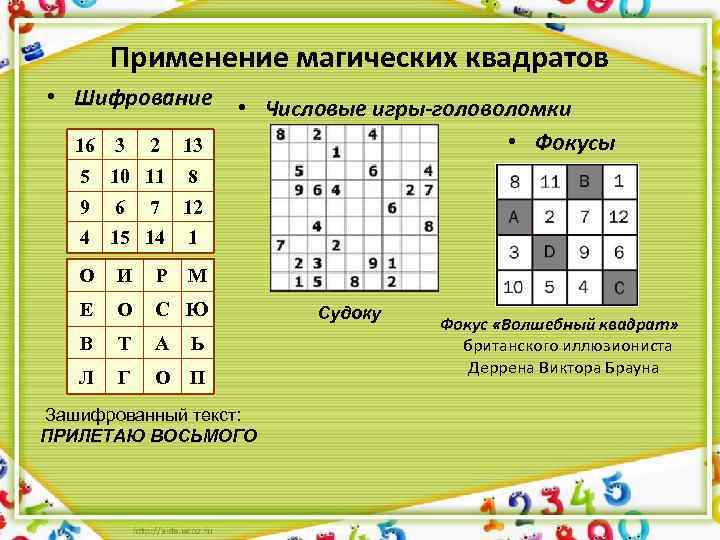Применение магических квадратов • Шифрование • Числовые игры-головоломки • Фокусы 16 3 2 13 5 10 11 8 9 6 7 12 4 15 14 1 О И Р М Е О С Ю В Т А Л Г О П Ь Зашифрованный текст: ПРИЛЕТАЮ ВОСЬМОГО Судоку Фокус «Волшебный квадрат» британского иллюзиониста Деррена Виктора Брауна
Применение магических квадратов • Магические квадраты и нанотехнологии Фирма "Toshiba» , разрабатывая качественные телевизионные экраны, пришла к выводу, что цветовые ячейки выгодно компоновать по принципу магических квадратов. В этом случае резко повышаются как четкость изображений, так и цветовые переходы.
Выводы: У чисел есть своя собственная жизнь и свои законы. Магические квадраты – это нечто удивительное, интересное и увлекательное. Заполнять магические квадраты несложно, но необходимо знать некоторые правила. У каждого квадрата свои свойства и тайны. Судоку – одна из интереснейших игр на свете. Она развивает мышление и логику в каждом из нас. Главными чертами магических квадратов являются не только ясность, чёткость и логика, но и эстетичность, стройность и красота. Законы квадратов отражают законы красоты.
Выводы: • В результате работы я подтвердил гипотезу о том, что существуют способы заполнения магических квадратов, изучив которые можно составить магический квадрат любого порядка. • Я изучил лишь небольшую часть способов составления магических квадратов, поэтому на этом я не собираюсь останавливаться. Есть еще много разных видов магических квадратов, которые я хотел бы в дальнейшем изучать. • Составление магических квадратов представляет собой отличную гимнастику для ума. Я обязательно должен научить и других тому, что умею сам.
Практическая значимость работы: • Материал этого исследования можно использовать на внеклассных занятиях для более широкого кругозора учеников, и как разминочные задания к началу урока, при подготовке к олимпиадам и интеллектуальным соревнованиям по математике. Задача о составлении магических квадратов, как одна из самых интересных математических головоломок, может привлечь внимание детей к новым головоломкам, к решению других занимательных задач по математике. • На основе этой работы можно в дальнейшем организовать кружок юных мыслителей. В действительности заинтересовать учащихся, привить любовь к математике.
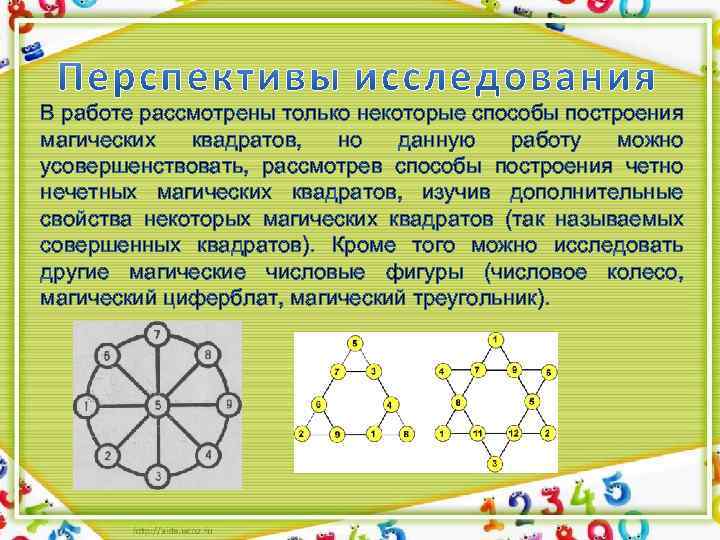В работе рассмотрены только некоторые способы построения магических квадратов, но данную работу можно усовершенствовать, рассмотрев способы построения четно нечетных магических квадратов, изучив дополнительные свойства некоторых магических квадратов (так называемых совершенных квадратов). Кроме того можно исследовать другие магические числовые фигуры (числовое колесо, магический циферблат, магический треугольник).