2 2 Nondeterministic Finite Accepters Definition 1 A

2. 2 Nondeterministic Finite Accepters Definition 1 A nondeterministic finite accepter or nfa　is defined by the quintuple • A string is accepted by an nfa if there is some sequence of possible moves that will put the machine in a final state at the end of the string. • A string is rejected by an nfa only if there is no possible sequence of moves by which a final state can be reached. Example 2. 8 a a a Nondeterministic a a a

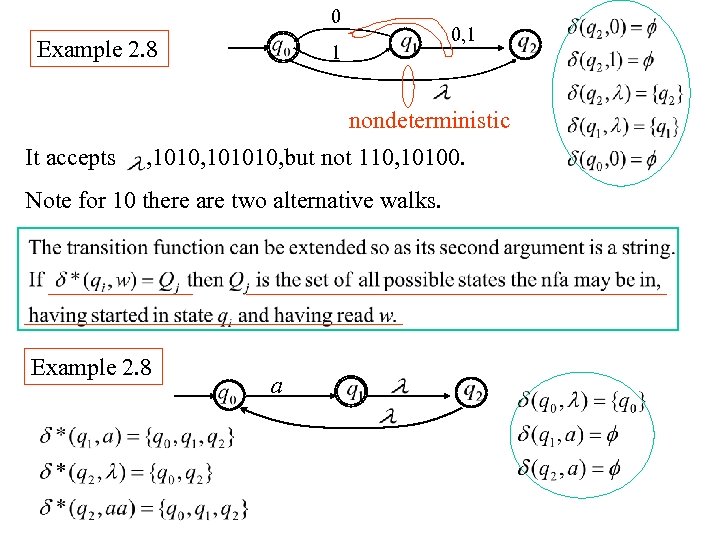0 Example 2. 8 0, 1 1 nondeterministic It accepts , 101010, but not 110, 10100. Note for 10 there are two alternative walks. Example 2. 8 a

Example　2. 10 Does this nfa accept string Find the language accepted by w=110? the following nfa. 0 1 Solution Dead Configuration!!! 0, 1

• Why Nondeterminism? (Digital computers are completely deterministic) 1. Nondeterministic machines is sometime helpful in solving problems easily. Example Search-and-backtrack algorithms

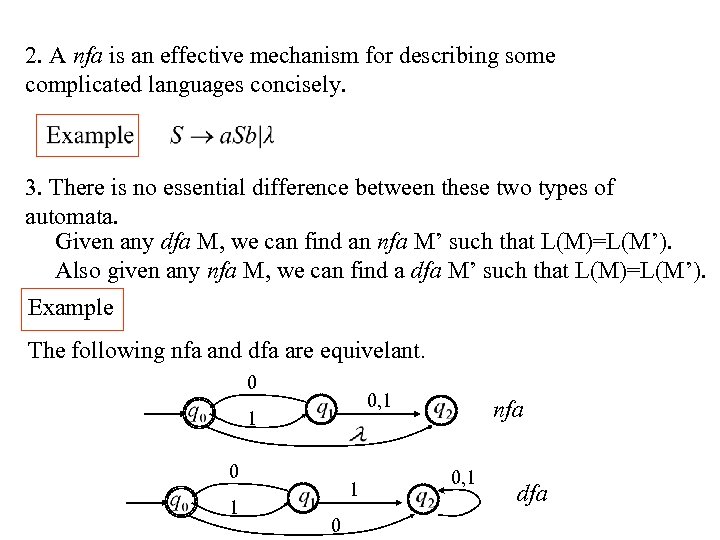2. A nfa is an effective mechanism for describing some complicated languages concisely. 3. There is no essential difference between these two types of automata. Given any dfa M, we can find an nfa M’ such that L(M)=L(M’). Also given any nfa M, we can find a dfa M’ such that L(M)=L(M’). Example The following nfa and dfa are equivelant． 0 0, 1 1 0 nfa 0, 1 dfa

Procedure to convert nfa to dfa 1. Creat a graph G(D) with vertex {q 0}. Identify this vertex as the initial vertex. 2. Repeat the following steps until no more edges are missing. 3. take any vertex{qi, qj, …, qk} of G(D) that has no outgoing edge for some 4. Compute 5. 6. create a vertex for G(D) labeled {ql, qm, …, qn} if it is not already exist. Add to G(D) an edge from {qi, qj, …, qk} to {ql, qm, …, qn} and label it with a. 7. 3. Every state of D(D) whose label contains any final vertex. 8. 4. If accepts is identified as a , the vertex {q 0} in G(D) is also made a final vertex.

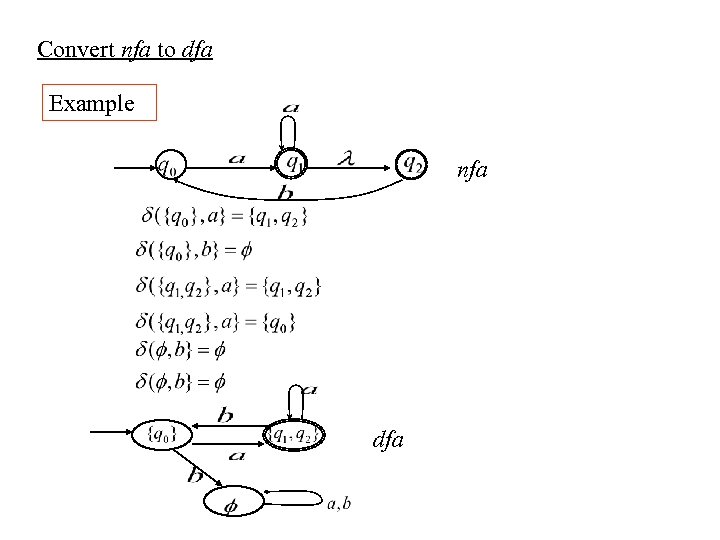Convert nfa to dfa Example nfa dfa

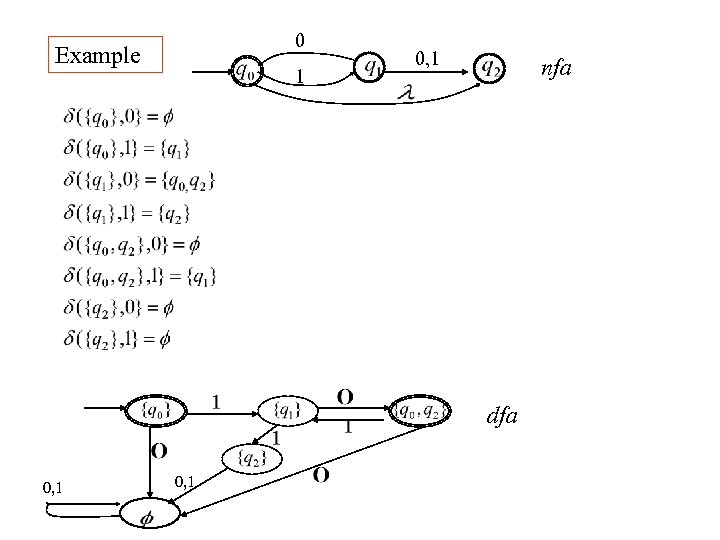0 Example 1 0, 1 nfa dfa 0, 1

Chapter 3 Regular Languages and Regular Grammars • We have known that a regular language can be described by some dfa. In this chapter we look at other ways of representing regular languages. 3. 1 Regular Expressions • Formal Definition of a Regular Expression Example 3. 1

• Language Associated with Regular Expressions Termination condition Reduce L(r ) to simpler components.

Example 3. 2 Exhibit the language L(a*・(a+b)) in set notation. Solution Ambiguity: Precedence rules: star-closure, concatenation, union low high Example 3. 3

Example 3. 4 Example 3. 5 Solution: Example 3. 6 Solution:

3. 2 Connection Between Regular Expressions and Regular Languages • Given regular expression r, we have defined a language L(r ). • A language is said to be regular, if it is accepted by a dfa (or by an nfa since dfa and nfa are equivalent). What is the relation between regular expressions and regular language? Regular languages Regular expressions Theorem 3. 1 Let r be a regular expression. Then there exists some nfa that accepts L(r ). Consequently, L(r ) is a regular language. Theorem 3. 2 Let L be a regular language. Then there exists a regular expression r such that L=L(r ).

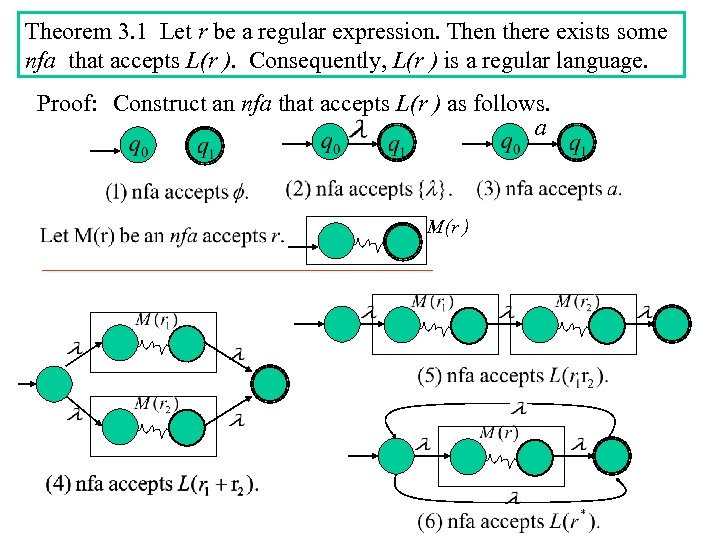Theorem 3. 1 Let r be a regular expression. Then there exists some nfa that accepts L(r ). Consequently, L(r ) is a regular language. Proof: 　Construct an nfa that accepts L(r ) as follows. a M(r )

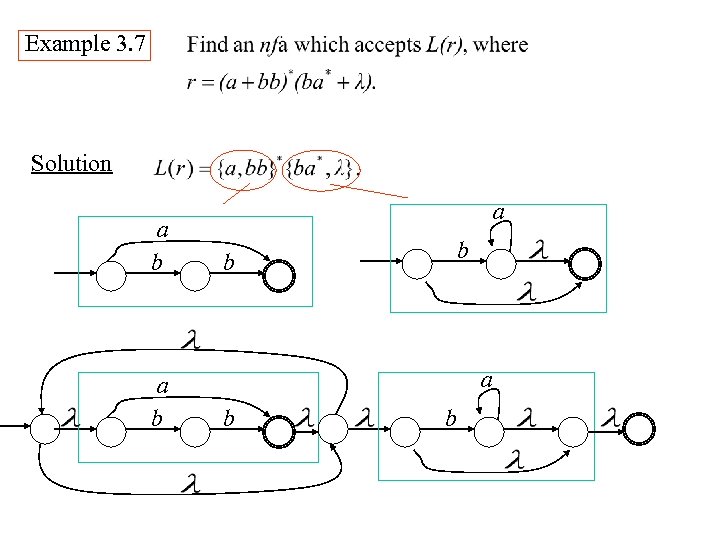Example 3. 7 Solution a b a b b

Theorem 3. 2 Let L be a regular language. Then there exists a regular expression r such that L=L(r ). Proof: 　Remove one vertex after the other between the initial one and e final one. Finally, we reach the following ce*b situation: ae*d 1 d a 2 c b 3 1 ce*d ae*b 3

Regular Expressions for Describing Simple Patterns Given a regular expression, we can find an nfa for recognizing it. This nfa can be reduced to a dfa.

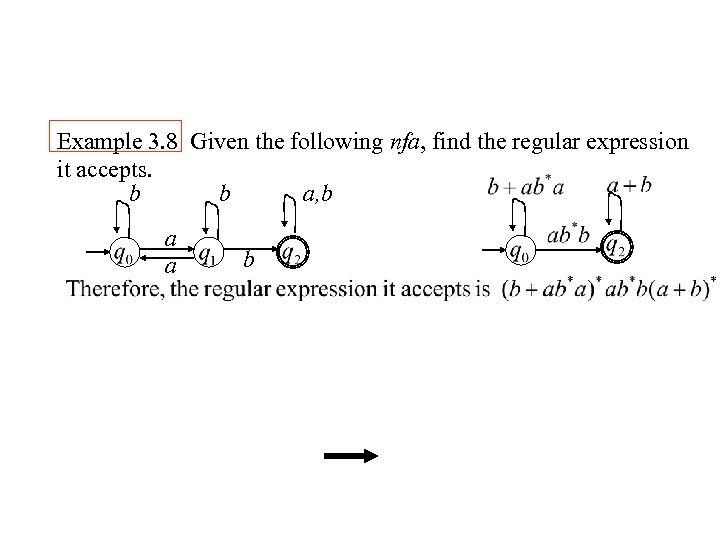Example 3. 8 Given the following nfa, find the regular expression it accepts. b b a, b a a b

3. 3 Regular Grammars • The third way of describing regular languages is by means of certain simple grammars. (what are the other two ways? ) Right- and Left-Linear Grammars

Right-linear Grammars Generate Regular Languages • Right-linear grammar Regular language • left-linear grammar Regular language Theorem 3. 3 Let G=(V, T, S, P) be a right-linear grammar. Then L(G) is a regular language. Policy of Proof: Construct an nfa which accepts L(G). V V’ a b b a

Theorem 3. 4 If L is a regular language on an alphabet , then there exists a right-linear grammar G=(V, , S, P) such that L=L(G). Policy of Proof: Let M be the dfa that accepts L. Construct the right-linear grammar G from M such that G generates L. Solution a a b a

Course Project 1: Design An Automatic Selling Machine Problem: There is a machine selling 3 types of drinks d 1, d 2, d 3, where the price for d 1 is 70 cents, for d 2 is 90 cents and for d 3 is 1 dollar. The buyers can use coins of 10 cents, 25 cents, 50 cents and 1 dollar. The number of drinks which a buyer can buy once from the machine is up to 3. Suppose that in the machine there is a place for inserting coins, a button for selecting the type of drinks and a button for selecting the number of drinks. To buy drinks, the buyer first insert money, then select the type of drinks, finally select the number of the drinking. (1) Suppose that , where c 1=10 cents, c 2=25 cents, c 3=50 cents, c 4=1 dollars, n 1=1, n 2=2, n 3=3. Write regular expression/language the machine accepts. (2) Design a DFA for the language in (1). (3) Design a regular grammar to generate the language in (1) (4) Write a program (using C++ or C#) to implement the DFA in (2) (5) (Optional) Change the program in (4) so that it gives the change to users. Requirement for the project: (1) A report with a detailed description for the requirements of the machine and for (1), (2), (3) and a program for (4). The program must have a using interface for a user to give an input and get an output (tell user if the buying is successful and give back the change and drinks). (2) Give a power point presentation.

Course Project 2: Design A Simple Calculator + - × 0 1 / 2 3 Problem: Design a simple calculator (see the figure). 4 5 6 7 Suppose that 8 9 ( ) (1) Design a regular expression r for the calculator. = . (2) Design a DFA for accepting the regular language L(r). (3) Design a regular grammar to generate the regular language L(r). (4) Write a program (using C++ or C#) to implement the DFA. Requirement for the project: (1) A report with a detailed description for (1), (2), (3) and a program for (4). The program must have a using interface for a user to give an input and get an output. (2) Give a power point presentation.

Chapter 4 Properties of Regular Language 4. 2 Elementary questions about regular languages Proof: We represent the language by some dfa, then test w to see if it is accepted by this dfa. Theorem 6 There exists an algorithm for determining whether a regular language, given in standard representation, is empty, finite, or infinite. Proof: (1) represent the language by some dfa. If there is a simple path from the initial vertex to any final vertex, then the language is not empty. (2) Find all the vertices that are the base of some cycle. If any of these are on a path from an initial to a final vertex, the language is infinite. Otherwise, it is finite.