lek_4.ppt
- Количество слайдов: 30

2. 2 Множественная линейная регрессия На любой экономический показатель чаще всего оказывает влияние не один, а несколько факторов. В этом случае вместо парной регрессии Y=f(X) рассматривается множественная регрессия Y=f(X 1, X 2, …, Xm). 1

Задача оценки статистической взаимосвязи переменных Y и X 1, X 2, …, Xm формулируется аналогично случаю парной регрессии. Уравнение множественной регрессии может быть представлено в виде Y=f( , X)+ , 2

где X=(X 1, X 2, …, Xm) – вектор независимых (объясняющих) переменных; - вектор параметров (подлежащих определению); - случайная ошибка (отклонение); Y – зависимая (объясняемая) переменная. 3

Самая простая из моделей множественной регрессии – модель множественной линейной регрессии. Теоретическое линейное уравнение регрессии имеет вид: Y= 0+ 1 X 1+ 2 X 2+…+ m. Xm+ или для индивидуальных наблюдений i, i=1, 2, …, n, yi= 0+ 1 xi 1+ 2 xi 2+…+ mxim+ i. 4

j, j=1, 2, …, m, называется j-м теоретическим коэффициентом регрессии (частичным коэффициентом регрессии). Он характеризует чувствительность величины Y к изменению Xj, т. е. отражает влияние на условное математическое ожидание M(Y) зависимой переменной Y объясняющей переменной Xj при условии, что все другие объясняющие переменные модели остаются постоянными. 5

0 – свободный член, определяющий значение Y в случае, когда все объясняющие переменные Xj равны нулю. После выбора линейной функции в качестве модели зависимости необходимо оценить параметры регрессии. 6

Если имеется n наблюдений вектора m объясняющих переменных X=(X 1, X 2, …, Xm) и зависимой переменной Y, то для однозначного отыскания вектора параметров должно выполняться неравенство n m+1. Число v=n-m-1 называется числом степеней свободы. 7

Самым распространённым методом оценки параметров уравнения множественной линейной регрессии является метод наименьших квадратов (МНК). 8

Предпосылки МНК 1. Математическое ожидание случайного отклонения i равно нулю для всех наблюдений: М( i)=0, i=1, 2, …, n. 2. Гомоскедастичность. Дисперсия случайных отклонений постоянна: D( i )=D( j)= 2 для любых наблюдений i и j. 9

3. Отсутствие автокорреляции. Случайные отклонения i и j являются независимыми друг от друга для всех i≠j. 4. Случайное отклонение должно быть независимо от объясняющих переменных. 5. Модель является линейной относительно параметров. 10

Для случая множественной линейной регрессии существенными являются ещё две предпосылки: 6. Отсутствие мультиколлинеарности. Между объясняющими переменными отсутствует строгая (сильная) линейная зависимость. 7. Ошибки i имеют нормальное распределение ( i~N(0, 2)). 11

Истинные значения параметров j по выборке получить невозможно, поэтому вместо теоретического уравнения регрессии оценивается эмпирическое уравнение регрессии: Y=b 0+b 1 X 1+b 2 X 2+…+bm. Xm+e , b 0, b 1, …, bm – оценки теоретических значений 0, 1, …, m коэффициентов регрессии (эмпирические коэффициенты регрессии); e – оценка отклонения . 12

При выполнении предпосылок МНК относительно ошибок i оценки b 0, b 1, …, bm параметров 0, 1, …, m множественной линейной регрессии по МНК являются несмещёнными, состоятельными и эффективными (т. е. BLUE-оценками). 13

Отклонение ei значения yi зависимой переменной Y от модельного значения , соответствующего уравнению регрессии в i- м наблюдении (i=1, 2, …, n), рассчитывается по формуле ei=yi-b 0 -b 1 xi 1 -…-bmxim. 14

Тогда по МНК для нахождения оценок b 0, b 1, …, bm минимизируется следующая функция: 15

Функция в матричной форме представима как произведение вектор-строки. на вектор-столбец e. Вектор-столбец e может быть записан в следующем виде: . 16

Отсюда получаем 17

Необходимым условием минимума функции Q является равенство нулю всех её частных производных по bj (j=1, …, m) и по b 0. Получаем систему m+1 линейных уравнений с m+1 неизвестными: 18
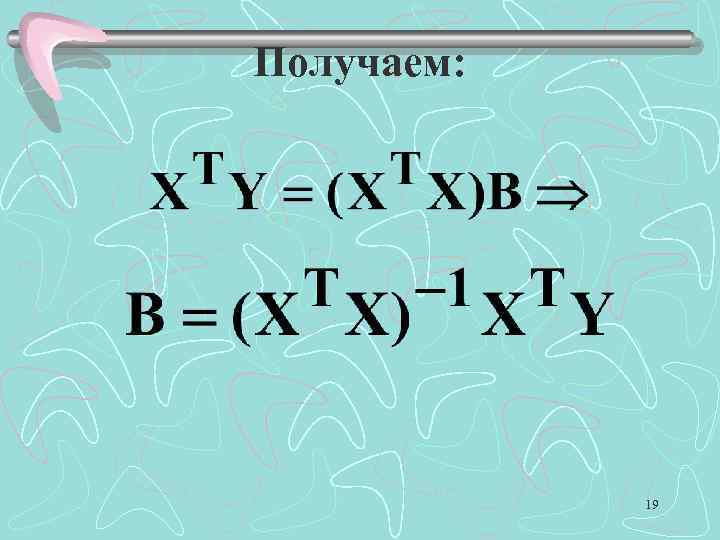
Получаем: 19
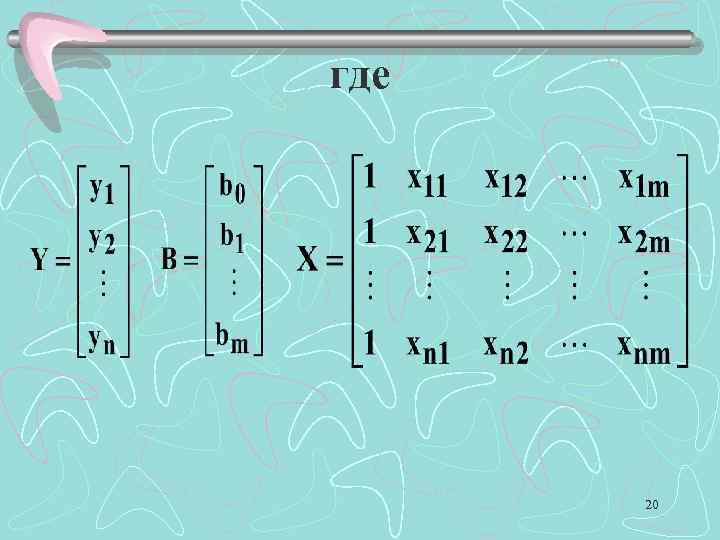
где 20

2. 2. 1 Дисперсии и стандартные ошибки коэффициентов Знания дисперсии и стандартных ошибок позволяет анализировать точность оценок, строить доверительные интервалы для теоретических коэффициентов, проверять соответствующие гипотезы. 21

Наиболее удобно формулы расчета данных характеристик приводить в матричной форме. Три первые предпосылки МНК в матричной форме будут иметь вид: 22
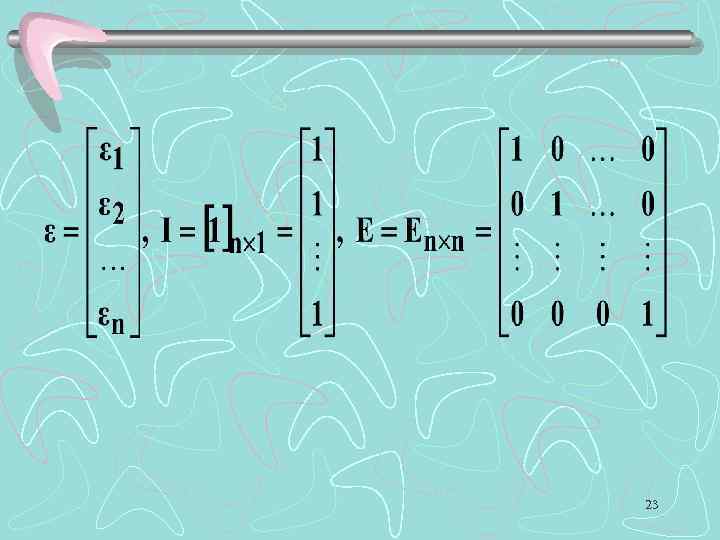
23
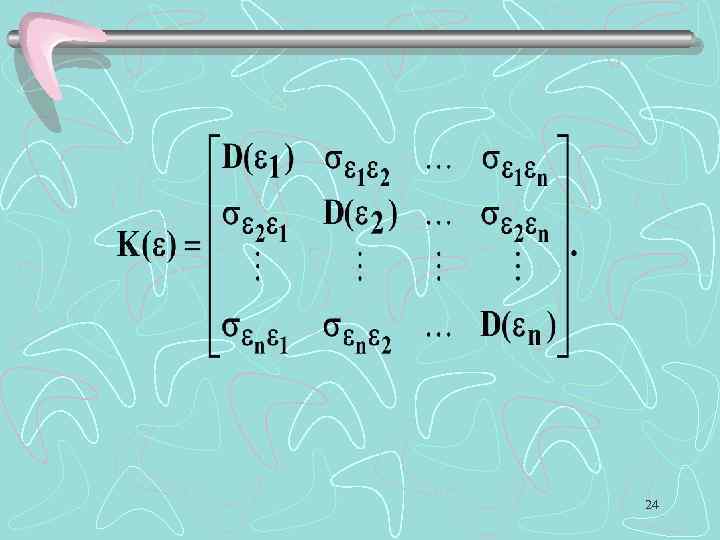
24

Эмпирические коэффициенты множественной линейной регрессии определяются по формуле Подставляя теоретические значения Y=X +ε в данное соотношение, имеем: 25

Следовательно, Построим дисперсионноковариационную матрицу В силу того, что Xj не являются случайными величинами, имеем: 26

где - j-й диагональный элемент матрицы 27

Поскольку истинное значение 2 по выборке дисперсии определить невозможно, оно заменяется соответствующей несмещенной оценкой 28

Следовательно, по выборке можно определить лишь выборочные дисперсии эмпирических коэффициентов регрессии: 29

Как и в случае парной регрессии, / называется стандартной ошибкой регрессии. называется стандартной ошибкой коэффициента регрессии. 30
lek_4.ppt