2 12 ПЛОЩАДЬ ПЛОСКОЙ ФИГУРЫ 1 Определение Плоская

2. 12. ПЛОЩАДЬ ПЛОСКОЙ ФИГУРЫ 1 Определение. Плоская фигура Q — часть плоскости, ограниченной простой замкнутой кривой. Многоугольник вписан в фигуру Q, если каждая точка этого многоугольника принадлежит фигуре Q или ее границе. Если все точки плоской фигуры и ее границы принадлежат некоторому многоугольнику, то будем говорить, что указанный многоугольник описан вокруг фигуры Q. P* = sup Si; P* = inf Sd Определение. Плоская фигура Q называется квадрируемой, если верхняя площадь P* этой фигуры совпадает с ее нижней площадью P*. При этом число Р = P* называется площадью фигуры Q. Теорема. Для того чтобы плоская фигура Q была квадрируемой, необходимо и достаточно, чтобы для любого положительного числа > 0 можно было указать такой описанный вокруг фигуры Q многоугольник и такой вписанный в фигуру Q многоугольник, разность Sd — Si площадей которых была бы меньше : Sd — Si < .

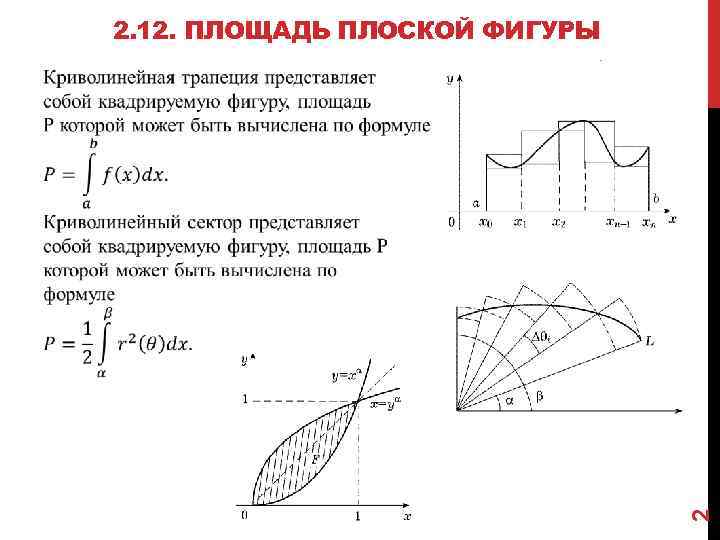2. 12. ПЛОЩАДЬ ПЛОСКОЙ ФИГУРЫ 2

2. 13. ОБЪЕМЫ ТЕЛ 3 Определение. Тело Е называется кубируемым, если верхний объем V* этого тела совпадает с нижним объемом V*. При этом число V = V* называется объемом тела Е. Теорема. Для того чтобы тело Е было кубируемым, необходимо и достаточно, чтобы для любого положительного числа > 0 можно было указать такой описанный вокруг тела Е многогранник и такой вписанный в тело Е многогранник, разность V* - V* объемов которых была бы меньше . Цилиндр - тело, ограниченное цилиндрической поверхностью с образующими, параллельными некоторой оси, и двумя плоскостями, перпендикулярными этой оси. Если основанием цилиндра Е является квадрируемая фигура Q, то цилиндр представляет собой кубируемое тело, причем объем V цилиндра Е равен Ph, где Р — площадь основания Q, a h — высота цилиндра.

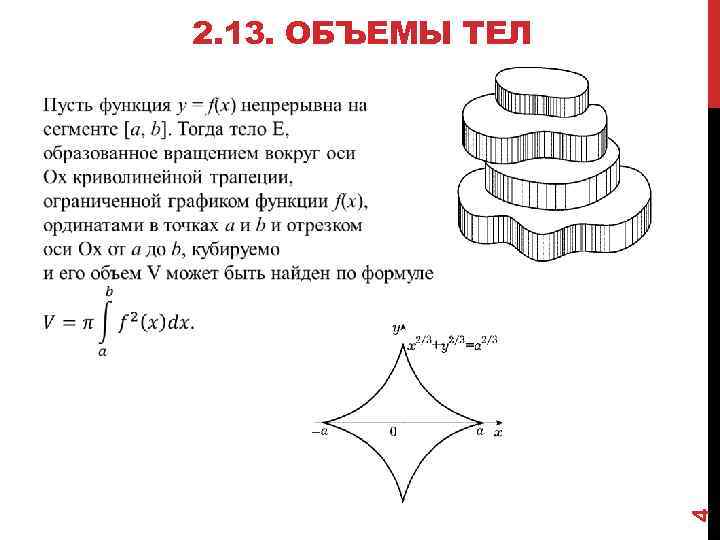2. 13. ОБЪЕМЫ ТЕЛ 4

2. 14. ПЛОЩАДИ ПОВЕРХНОСТЕЙ 5

2. 14. ПЛОЩАДИ ПОВЕРХНОСТЕЙ 6

3. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ 7

3. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ 8

3. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ 9

3. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ 10

3. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ 11

3. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ 12

3. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ 13

3. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ 14

3. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ 15