703d112af119448c474e0b3ee15f2a7a.ppt
- Количество слайдов: 56
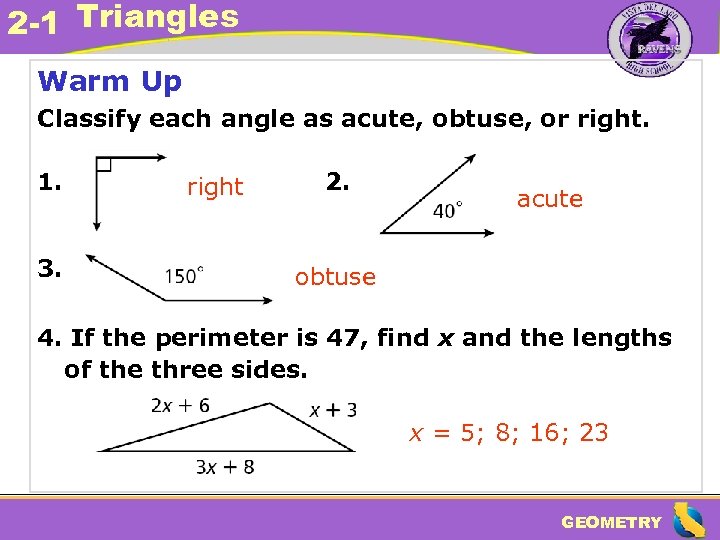 2 -1 Triangles Warm Up Classify each angle as acute, obtuse, or right. 1. 3. right 2. acute obtuse 4. If the perimeter is 47, find x and the lengths of the three sides. x = 5; 8; 16; 23 GEOMETRY
2 -1 Triangles Warm Up Classify each angle as acute, obtuse, or right. 1. 3. right 2. acute obtuse 4. If the perimeter is 47, find x and the lengths of the three sides. x = 5; 8; 16; 23 GEOMETRY
 2 -1 Triangles 1. 2. In the figure, n is a whole number. What is the smallest possible value for n? A sewing club is making a quilt consisting of 25 squares with each side of the square measuring 30 centimeters. If the quilt has five rows and five columns, what is the perimeter of the quilt? GEOMETRY
2 -1 Triangles 1. 2. In the figure, n is a whole number. What is the smallest possible value for n? A sewing club is making a quilt consisting of 25 squares with each side of the square measuring 30 centimeters. If the quilt has five rows and five columns, what is the perimeter of the quilt? GEOMETRY
 2 -1 Triangles 1. In the figure, n is a whole number. What is the smallest possible value for n? GEOMETRY
2 -1 Triangles 1. In the figure, n is a whole number. What is the smallest possible value for n? GEOMETRY
 2 -1 Triangles 2. A sewing club is making a quilt consisting of 25 squares with each side of the square measuring 30 centimeters. If the quilt has five rows and five columns, what is the perimeter of the quilt? GEOMETRY
2 -1 Triangles 2. A sewing club is making a quilt consisting of 25 squares with each side of the square measuring 30 centimeters. If the quilt has five rows and five columns, what is the perimeter of the quilt? GEOMETRY
 2 -1 Triangles Objectives Classify triangles by their angle measures and side lengths. Use triangle classification to find angle measures and side lengths. GEOMETRY
2 -1 Triangles Objectives Classify triangles by their angle measures and side lengths. Use triangle classification to find angle measures and side lengths. GEOMETRY
 2 -1 Triangles Vocabulary acute triangle equiangular triangle right triangle obtuse triangle equilateral triangle isosceles triangle scalene triangle GEOMETRY
2 -1 Triangles Vocabulary acute triangle equiangular triangle right triangle obtuse triangle equilateral triangle isosceles triangle scalene triangle GEOMETRY
 2 -1 Triangles California Standards 12. 0 Students find and use measures of sides and of interior and exterior angles of triangles and polygons to classify figures and solve problems. 15. 0 Students use the Pythagorean theorem to determine distance and find missing lengths of sides of right triangles. GEOMETRY
2 -1 Triangles California Standards 12. 0 Students find and use measures of sides and of interior and exterior angles of triangles and polygons to classify figures and solve problems. 15. 0 Students use the Pythagorean theorem to determine distance and find missing lengths of sides of right triangles. GEOMETRY
 2 -1 Triangles Recall that a triangle ( ) is a polygon with three sides. Triangles can be classified in two ways: by their angle measures or by their side lengths. GEOMETRY
2 -1 Triangles Recall that a triangle ( ) is a polygon with three sides. Triangles can be classified in two ways: by their angle measures or by their side lengths. GEOMETRY
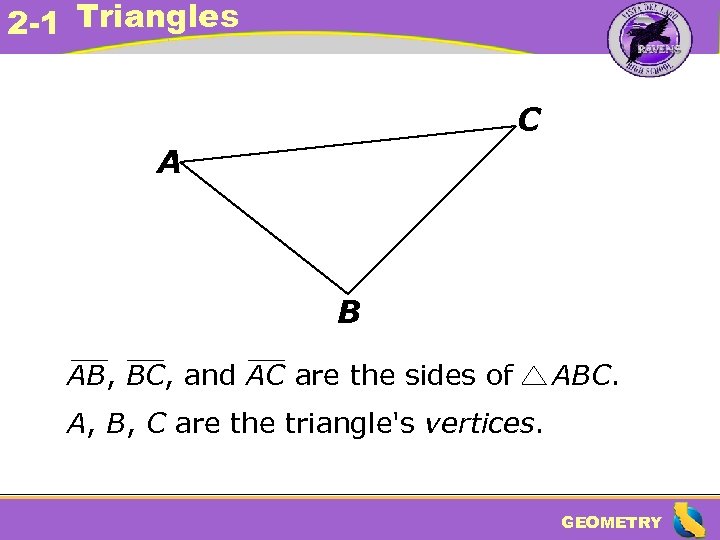 2 -1 Triangles C A B AB, BC, and AC are the sides of ABC. A, B, C are the triangle's vertices. GEOMETRY
2 -1 Triangles C A B AB, BC, and AC are the sides of ABC. A, B, C are the triangle's vertices. GEOMETRY
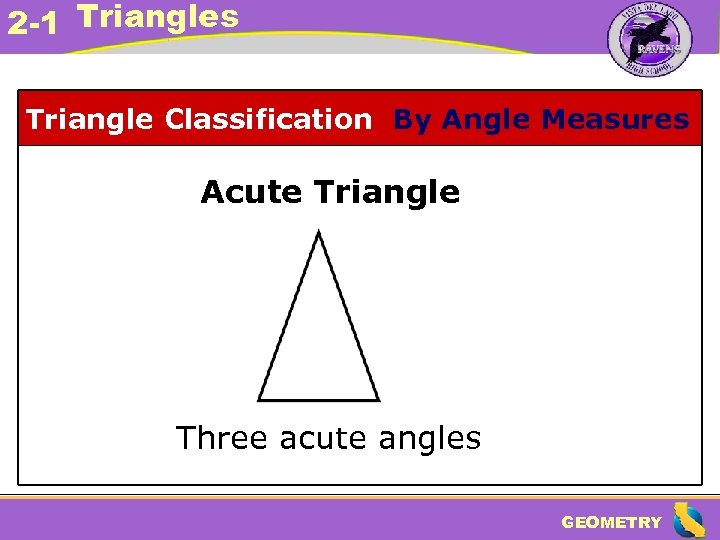 2 -1 Triangles Triangle Classification By Angle Measures Acute Triangle Three acute angles GEOMETRY
2 -1 Triangles Triangle Classification By Angle Measures Acute Triangle Three acute angles GEOMETRY
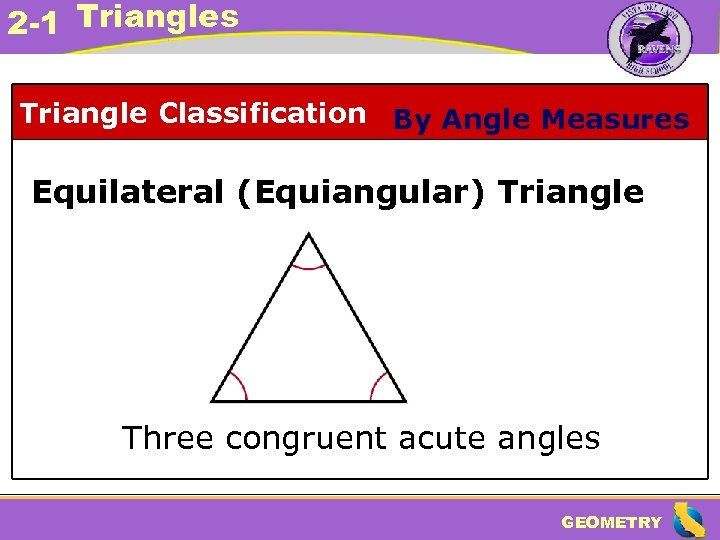 2 -1 Triangles Triangle Classification By Angle Measures Equilateral (Equiangular) Triangle Three congruent acute angles GEOMETRY
2 -1 Triangles Triangle Classification By Angle Measures Equilateral (Equiangular) Triangle Three congruent acute angles GEOMETRY
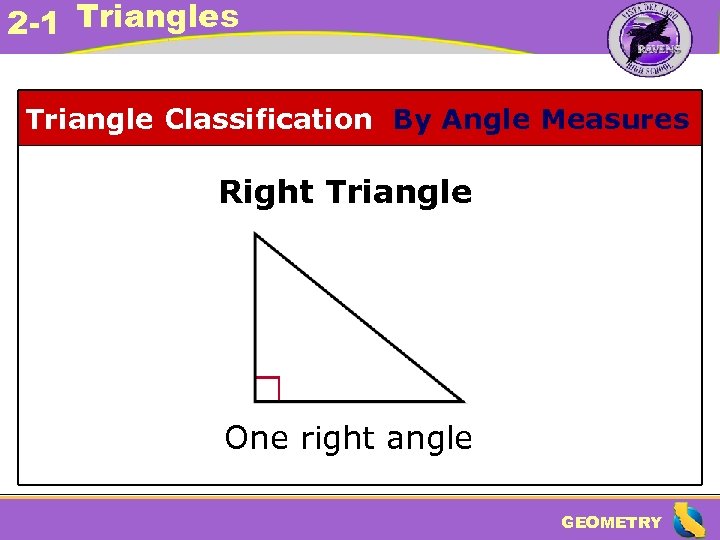 2 -1 Triangles Triangle Classification By Angle Measures Right Triangle One right angle GEOMETRY
2 -1 Triangles Triangle Classification By Angle Measures Right Triangle One right angle GEOMETRY
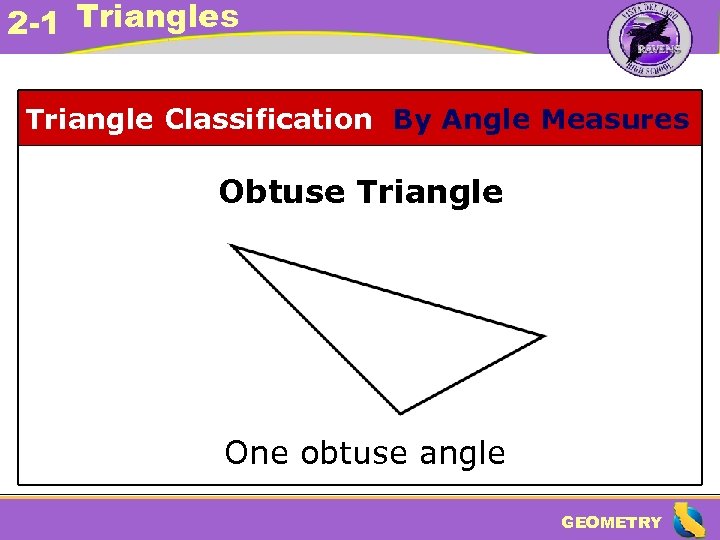 2 -1 Triangles Triangle Classification By Angle Measures Obtuse Triangle One obtuse angle GEOMETRY
2 -1 Triangles Triangle Classification By Angle Measures Obtuse Triangle One obtuse angle GEOMETRY
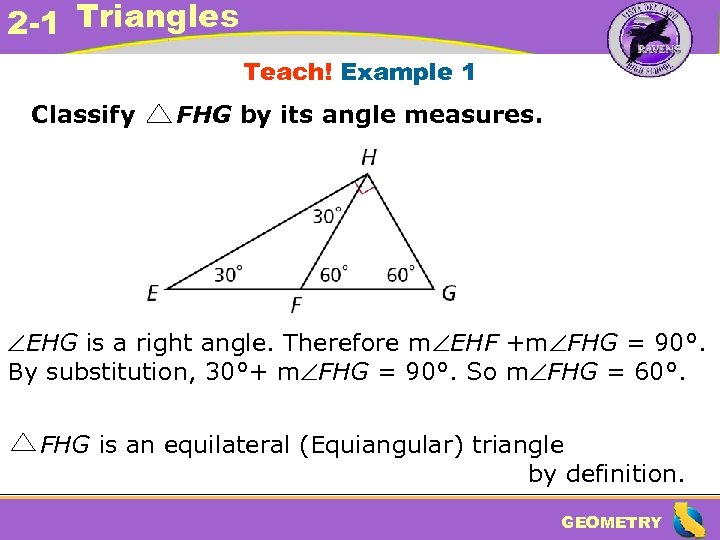 2 -1 Triangles Teach! Example 1 Classify FHG by its angle measures. EHG is a right angle. Therefore m EHF +m FHG = 90°. By substitution, 30°+ m FHG = 90°. So m FHG = 60°. FHG is an equilateral (Equiangular) triangle by definition. GEOMETRY
2 -1 Triangles Teach! Example 1 Classify FHG by its angle measures. EHG is a right angle. Therefore m EHF +m FHG = 90°. By substitution, 30°+ m FHG = 90°. So m FHG = 60°. FHG is an equilateral (Equiangular) triangle by definition. GEOMETRY
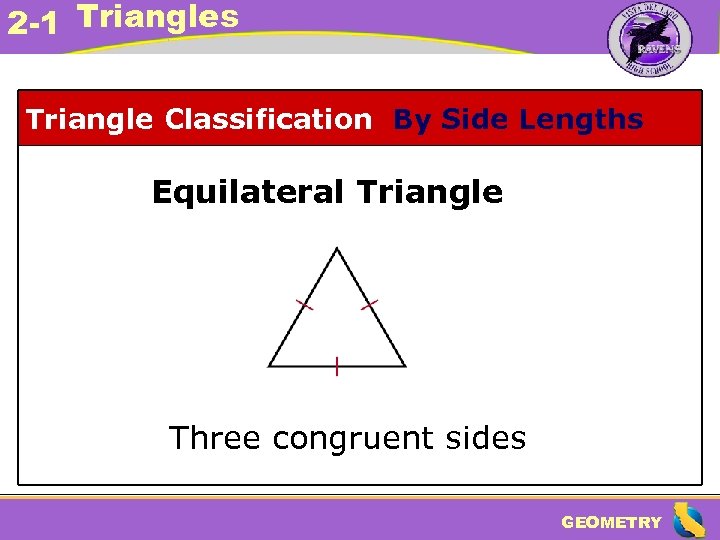 2 -1 Triangles Triangle Classification By Side Lengths Equilateral Triangle Three congruent sides GEOMETRY
2 -1 Triangles Triangle Classification By Side Lengths Equilateral Triangle Three congruent sides GEOMETRY
 2 -1 Triangles Triangle Classification By Side Lengths Isosceles Triangle At least two congruent sides GEOMETRY
2 -1 Triangles Triangle Classification By Side Lengths Isosceles Triangle At least two congruent sides GEOMETRY
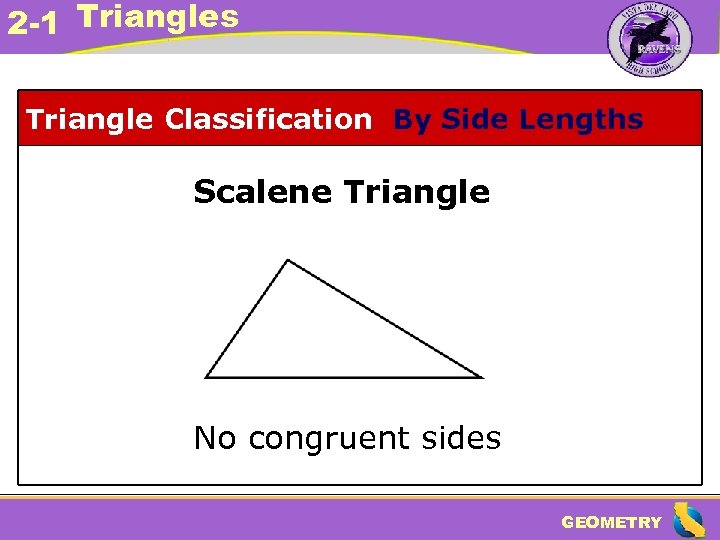 2 -1 Triangles Triangle Classification By Side Lengths Scalene Triangle No congruent sides GEOMETRY
2 -1 Triangles Triangle Classification By Side Lengths Scalene Triangle No congruent sides GEOMETRY
 2 -1 Triangles Remember! When you look at a figure, you cannot assume segments are congruent based on appearance. They must be marked as congruent. GEOMETRY
2 -1 Triangles Remember! When you look at a figure, you cannot assume segments are congruent based on appearance. They must be marked as congruent. GEOMETRY
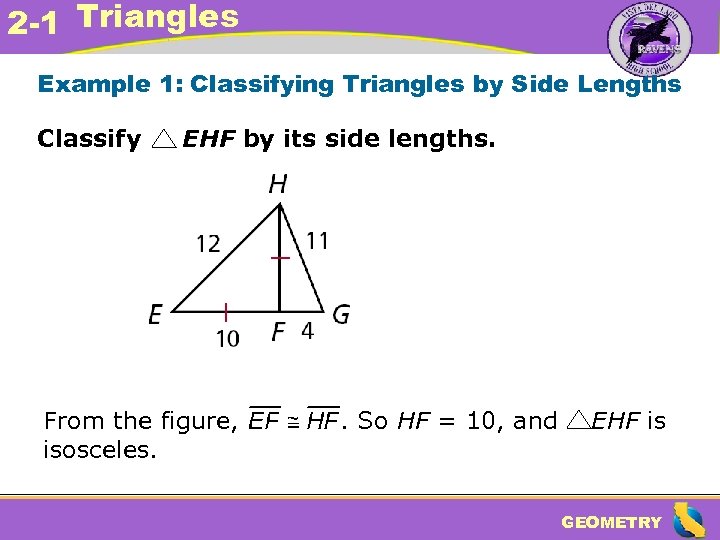 2 -1 Triangles Example 1: Classifying Triangles by Side Lengths Classify EHF by its side lengths. From the figure, isosceles. . So HF = 10, and EHF is GEOMETRY
2 -1 Triangles Example 1: Classifying Triangles by Side Lengths Classify EHF by its side lengths. From the figure, isosceles. . So HF = 10, and EHF is GEOMETRY
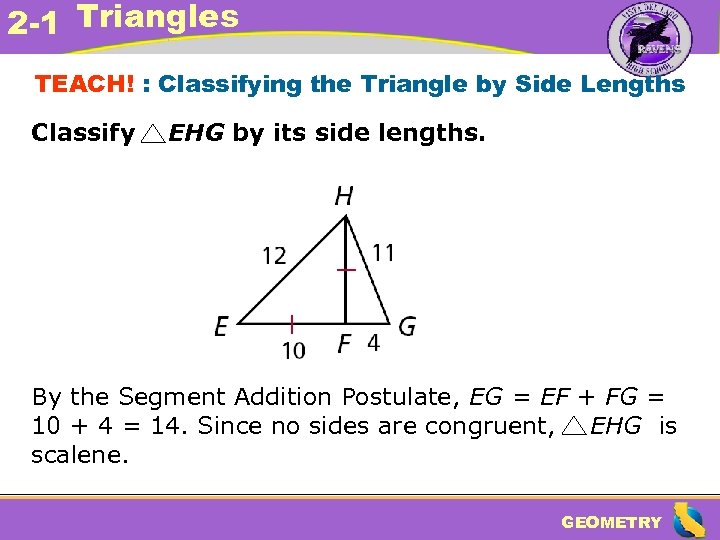 2 -1 Triangles TEACH! : Classifying the Triangle by Side Lengths Classify EHG by its side lengths. By the Segment Addition Postulate, EG = EF + FG = 10 + 4 = 14. Since no sides are congruent, EHG is scalene. GEOMETRY
2 -1 Triangles TEACH! : Classifying the Triangle by Side Lengths Classify EHG by its side lengths. By the Segment Addition Postulate, EG = EF + FG = 10 + 4 = 14. Since no sides are congruent, EHG is scalene. GEOMETRY
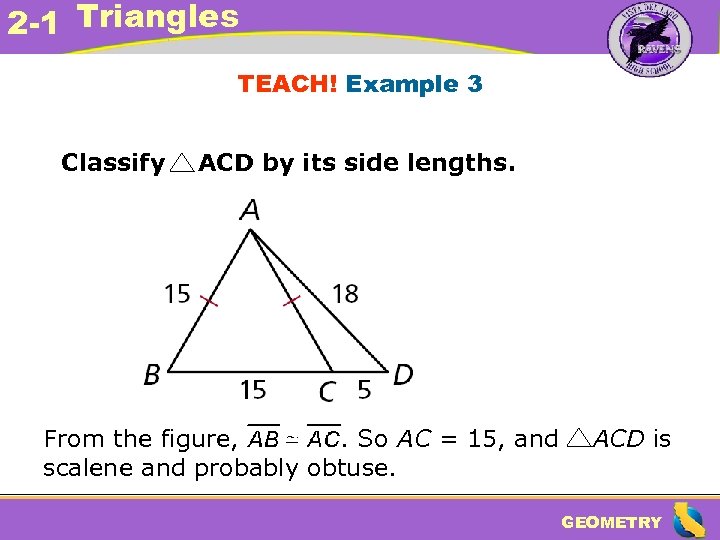 2 -1 Triangles TEACH! Example 3 Classify ACD by its side lengths. From the figure, . So AC = 15, and scalene and probably obtuse. ACD is GEOMETRY
2 -1 Triangles TEACH! Example 3 Classify ACD by its side lengths. From the figure, . So AC = 15, and scalene and probably obtuse. ACD is GEOMETRY
 2 -1 Triangles Example 3: Using Triangle Classification Find the side lengths of JKL. Step 1 Find the value of x. Given. Def. of segs. Substitute (4 x – 10. 7) for 4 x – 10. 7 = 2 x + 6. 3 JK and (2 x + 6. 3) for KL. JK = KL 2 x = 17. 0 x = 8. 5 Add 10. 7 and subtract 2 x from both sides. Divide both sides by 2. GEOMETRY
2 -1 Triangles Example 3: Using Triangle Classification Find the side lengths of JKL. Step 1 Find the value of x. Given. Def. of segs. Substitute (4 x – 10. 7) for 4 x – 10. 7 = 2 x + 6. 3 JK and (2 x + 6. 3) for KL. JK = KL 2 x = 17. 0 x = 8. 5 Add 10. 7 and subtract 2 x from both sides. Divide both sides by 2. GEOMETRY
 2 -1 Triangles Example 3 Continued Find the side lengths of JKL. Step 2 Substitute 8. 5 into the expressions to find the side lengths. JK = 4 x – 10. 7 = 4(8. 5) – 10. 7 = 23. 3 KL = 2 x + 6. 3 = 2(8. 5) + 6. 3 = 23. 3 JL = 5 x + 2 = 5(8. 5) + 2 = 44. 5 GEOMETRY
2 -1 Triangles Example 3 Continued Find the side lengths of JKL. Step 2 Substitute 8. 5 into the expressions to find the side lengths. JK = 4 x – 10. 7 = 4(8. 5) – 10. 7 = 23. 3 KL = 2 x + 6. 3 = 2(8. 5) + 6. 3 = 23. 3 JL = 5 x + 2 = 5(8. 5) + 2 = 44. 5 GEOMETRY
 2 -1 Triangles TEACH! Example 3 Find the side lengths of equilateral FGH. Step 1 Find the value of y. Given. FG = GH = FH Def. of segs. Substitute 3 y – 4 = 2 y + 3 (3 y – 4) for FG and (2 y + 3) for GH. y=7 Add 4 and subtract 2 y from both sides. GEOMETRY
2 -1 Triangles TEACH! Example 3 Find the side lengths of equilateral FGH. Step 1 Find the value of y. Given. FG = GH = FH Def. of segs. Substitute 3 y – 4 = 2 y + 3 (3 y – 4) for FG and (2 y + 3) for GH. y=7 Add 4 and subtract 2 y from both sides. GEOMETRY
 2 -1 Triangles TEACH! Example 3 Continued Find the side lengths of equilateral FGH. Step 2 Substitute 7 into the expressions to find the side lengths. FG = 3 y – 4 = 3(7) – 4 = 17 GH = 2 y + 3 = 2(7) + 3 = 17 FH = 5 y – 18 = 5(7) – 18 = 17 GEOMETRY
2 -1 Triangles TEACH! Example 3 Continued Find the side lengths of equilateral FGH. Step 2 Substitute 7 into the expressions to find the side lengths. FG = 3 y – 4 = 3(7) – 4 = 17 GH = 2 y + 3 = 2(7) + 3 = 17 FH = 5 y – 18 = 5(7) – 18 = 17 GEOMETRY
 2 -1 Triangles Example 4: Application A steel mill produces roof supports by welding pieces of steel beams into equilateral triangles. Each side of the triangle is 18 feet long. How many triangles can be formed from 420 feet of steel beam? The amount of steel needed to make one triangle is equal to the perimeter P of the equilateral triangle. P = 3(18) P = 54 ft GEOMETRY
2 -1 Triangles Example 4: Application A steel mill produces roof supports by welding pieces of steel beams into equilateral triangles. Each side of the triangle is 18 feet long. How many triangles can be formed from 420 feet of steel beam? The amount of steel needed to make one triangle is equal to the perimeter P of the equilateral triangle. P = 3(18) P = 54 ft GEOMETRY
 2 -1 Triangles Example 4: Application Continued A steel mill produces roof supports by welding pieces of steel beams into equilateral triangles. Each side of the triangle is 18 feet long. How many triangles can be formed from 420 feet of steel beam? To find the number of triangles that can be made from 420 feet of steel beam, divide 420 by the amount of steel needed for one triangle. 420 54 = 7 79 triangles There is not enough steel to complete an eighth triangle. So the steel mill can make 7 triangles from a 420 ft. piece of steel beam. GEOMETRY
2 -1 Triangles Example 4: Application Continued A steel mill produces roof supports by welding pieces of steel beams into equilateral triangles. Each side of the triangle is 18 feet long. How many triangles can be formed from 420 feet of steel beam? To find the number of triangles that can be made from 420 feet of steel beam, divide 420 by the amount of steel needed for one triangle. 420 54 = 7 79 triangles There is not enough steel to complete an eighth triangle. So the steel mill can make 7 triangles from a 420 ft. piece of steel beam. GEOMETRY
 2 -1 Triangles TEACH! Example 4 Each measure is the side length of an equilateral triangle. Determine how many 7 in. triangles can be formed from a 100 in. piece of steel. The amount of steel needed to make one triangle is equal to the perimeter P of the equilateral triangle. P = 3(7) P = 21 in. GEOMETRY
2 -1 Triangles TEACH! Example 4 Each measure is the side length of an equilateral triangle. Determine how many 7 in. triangles can be formed from a 100 in. piece of steel. The amount of steel needed to make one triangle is equal to the perimeter P of the equilateral triangle. P = 3(7) P = 21 in. GEOMETRY
 2 -1 Triangles TEACH! Example 4 Continued Each measure is the side length of an equilateral triangle. Determine how many 7 in. triangles can be formed from a 100 in. piece of steel. To find the number of triangles that can be made from 100 inches of steel, divide 100 by the amount of steel needed for one triangle. 100 7 = 2 14 7 triangles There is not enough steel to complete a fifteenth triangle. So the manufacturer can make 14 triangles from a 100 in. piece of steel. GEOMETRY
2 -1 Triangles TEACH! Example 4 Continued Each measure is the side length of an equilateral triangle. Determine how many 7 in. triangles can be formed from a 100 in. piece of steel. To find the number of triangles that can be made from 100 inches of steel, divide 100 by the amount of steel needed for one triangle. 100 7 = 2 14 7 triangles There is not enough steel to complete a fifteenth triangle. So the manufacturer can make 14 triangles from a 100 in. piece of steel. GEOMETRY
 2 -1 Triangles TEACH! Example 5 Each measure is the side length of an equilateral triangle. Determine how many 10 in. triangles can be formed from a 100 in. piece of steel. The amount of steel needed to make one triangle is equal to the perimeter P of the equilateral triangle. P = 3(10) P = 30 in. GEOMETRY
2 -1 Triangles TEACH! Example 5 Each measure is the side length of an equilateral triangle. Determine how many 10 in. triangles can be formed from a 100 in. piece of steel. The amount of steel needed to make one triangle is equal to the perimeter P of the equilateral triangle. P = 3(10) P = 30 in. GEOMETRY
 2 -1 Triangles TEACH! Example 5 Continued Each measure is the side length of an equilateral triangle. Determine how many 10 in. triangles can be formed from a 100 in. piece of steel. To find the number of triangles that can be made from 100 inches of steel, divide 100 by the amount of steel needed for one triangle. 100 10 = 10 triangles The manufacturer can make 10 triangles from a 100 in. piece of steel. GEOMETRY
2 -1 Triangles TEACH! Example 5 Continued Each measure is the side length of an equilateral triangle. Determine how many 10 in. triangles can be formed from a 100 in. piece of steel. To find the number of triangles that can be made from 100 inches of steel, divide 100 by the amount of steel needed for one triangle. 100 10 = 10 triangles The manufacturer can make 10 triangles from a 100 in. piece of steel. GEOMETRY
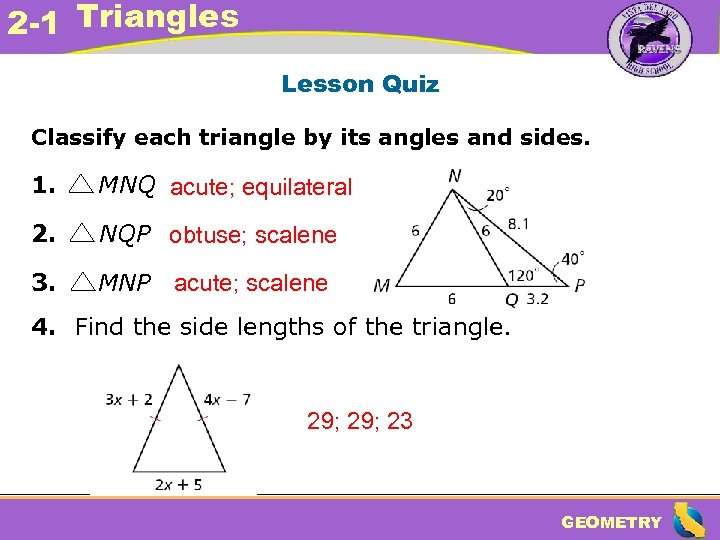 2 -1 Triangles Lesson Quiz Classify each triangle by its angles and sides. 1. MNQ acute; equilateral 2. NQP obtuse; scalene 3. MNP acute; scalene 4. Find the side lengths of the triangle. 29; 23 GEOMETRY
2 -1 Triangles Lesson Quiz Classify each triangle by its angles and sides. 1. MNQ acute; equilateral 2. NQP obtuse; scalene 3. MNP acute; scalene 4. Find the side lengths of the triangle. 29; 23 GEOMETRY
 2 -1 Triangles GEOMETRY
2 -1 Triangles GEOMETRY
 2 -1 Triangles Warm Up 1. Find the measure of exterior DBA of BCD, if m DBC = 30°, m C= 70°, and m D = 80°. 150° 2. What is the complement of an angle with measure 17°? 73° 3. How many lines can be drawn through N parallel to MP? Why? 1; Parallel Post. GEOMETRY
2 -1 Triangles Warm Up 1. Find the measure of exterior DBA of BCD, if m DBC = 30°, m C= 70°, and m D = 80°. 150° 2. What is the complement of an angle with measure 17°? 73° 3. How many lines can be drawn through N parallel to MP? Why? 1; Parallel Post. GEOMETRY
 2 -1 Triangles Objectives Find the measures of interior and exterior angles of triangles. Apply theorems about the interior and exterior angles of triangles. GEOMETRY
2 -1 Triangles Objectives Find the measures of interior and exterior angles of triangles. Apply theorems about the interior and exterior angles of triangles. GEOMETRY
 2 -1 Triangles Vocabulary auxiliary line corollary interior exterior interior angle exterior angle remote interior angle GEOMETRY
2 -1 Triangles Vocabulary auxiliary line corollary interior exterior interior angle exterior angle remote interior angle GEOMETRY
 2 -1 Triangles GEOMETRY
2 -1 Triangles GEOMETRY
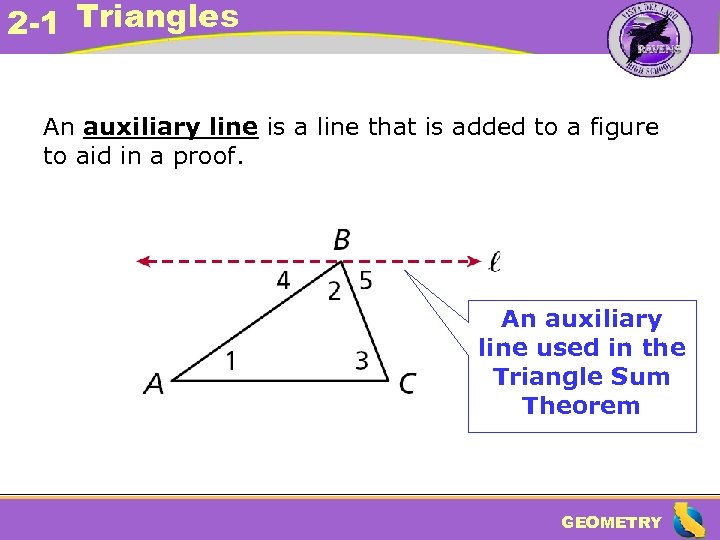 2 -1 Triangles An auxiliary line is a line that is added to a figure to aid in a proof. An auxiliary line used in the Triangle Sum Theorem GEOMETRY
2 -1 Triangles An auxiliary line is a line that is added to a figure to aid in a proof. An auxiliary line used in the Triangle Sum Theorem GEOMETRY
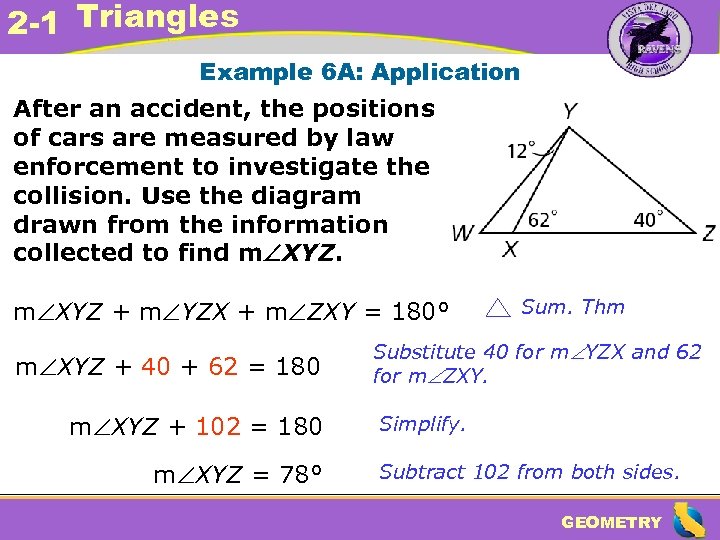 2 -1 Triangles Example 6 A: Application After an accident, the positions of cars are measured by law enforcement to investigate the collision. Use the diagram drawn from the information collected to find m XYZ + m YZX + m ZXY = 180° m XYZ + 40 + 62 = 180 m XYZ + 102 = 180 m XYZ = 78° Sum. Thm Substitute 40 for m YZX and 62 for m ZXY. Simplify. Subtract 102 from both sides. GEOMETRY
2 -1 Triangles Example 6 A: Application After an accident, the positions of cars are measured by law enforcement to investigate the collision. Use the diagram drawn from the information collected to find m XYZ + m YZX + m ZXY = 180° m XYZ + 40 + 62 = 180 m XYZ + 102 = 180 m XYZ = 78° Sum. Thm Substitute 40 for m YZX and 62 for m ZXY. Simplify. Subtract 102 from both sides. GEOMETRY
 2 -1 Triangles TEACH! Example 6 Use the diagram to find m MJK + m JKM + m KMJ = 180° m MJK + 104 + 44= 180 Sum. Thm Substitute 104 for m JKM and 44 for m KMJ. m MJK + 148 = 180 Simplify. m MJK = 32° Subtract 148 from both sides. GEOMETRY
2 -1 Triangles TEACH! Example 6 Use the diagram to find m MJK + m JKM + m KMJ = 180° m MJK + 104 + 44= 180 Sum. Thm Substitute 104 for m JKM and 44 for m KMJ. m MJK + 148 = 180 Simplify. m MJK = 32° Subtract 148 from both sides. GEOMETRY
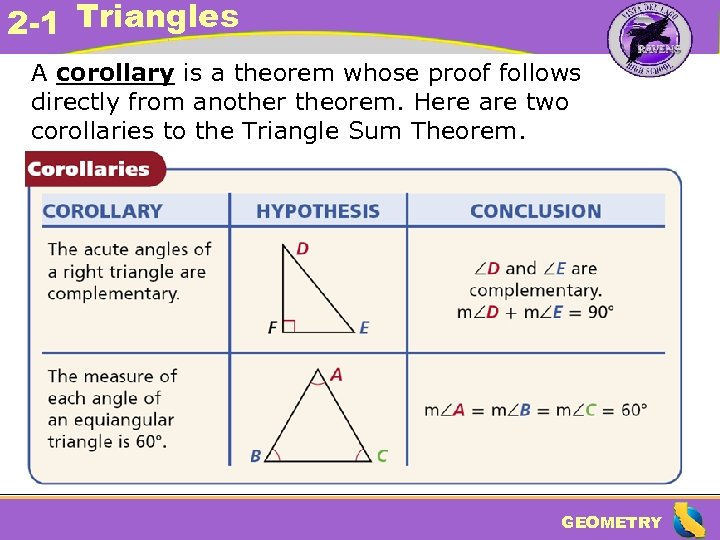 2 -1 Triangles A corollary is a theorem whose proof follows directly from another theorem. Here are two corollaries to the Triangle Sum Theorem. GEOMETRY
2 -1 Triangles A corollary is a theorem whose proof follows directly from another theorem. Here are two corollaries to the Triangle Sum Theorem. GEOMETRY
 2 -1 Triangles Example 7: Finding Angle Measures in Right Triangles One of the acute angles in a right triangle measures 2 x°. What is the measure of the other acute angle? Let the acute angles be A and B, with m A = 2 x°. m A + m B = 90° 2 x + m B = 90 Acute s of rt. are comp. Substitute 2 x for m A. m B = (90 – 2 x)° Subtract 2 x from both sides. GEOMETRY
2 -1 Triangles Example 7: Finding Angle Measures in Right Triangles One of the acute angles in a right triangle measures 2 x°. What is the measure of the other acute angle? Let the acute angles be A and B, with m A = 2 x°. m A + m B = 90° 2 x + m B = 90 Acute s of rt. are comp. Substitute 2 x for m A. m B = (90 – 2 x)° Subtract 2 x from both sides. GEOMETRY
 2 -1 Triangles TEACH! Example 7 a The measure of one of the acute angles in a right triangle is 63. 7°. What is the measure of the other acute angle? Let the acute angles be A and B, with m A = 63. 7°. m A + m B = 90° Acute s of rt. 63. 7 + m B = 90 Substitute 63. 7 for m A. m B = 26. 3° are comp. Subtract 63. 7 from both sides. GEOMETRY
2 -1 Triangles TEACH! Example 7 a The measure of one of the acute angles in a right triangle is 63. 7°. What is the measure of the other acute angle? Let the acute angles be A and B, with m A = 63. 7°. m A + m B = 90° Acute s of rt. 63. 7 + m B = 90 Substitute 63. 7 for m A. m B = 26. 3° are comp. Subtract 63. 7 from both sides. GEOMETRY
 2 -1 Triangles TEACH! Example 7 b The measure of one of the acute angles in a right triangle is x°. What is the measure of the other acute angle? Let the acute angles be A and B, with m A = x°. m A + m B = 90° x + m B = 90 m B = (90 – x)° Acute s of rt. are comp. Substitute x for m A. Subtract x from both sides. GEOMETRY
2 -1 Triangles TEACH! Example 7 b The measure of one of the acute angles in a right triangle is x°. What is the measure of the other acute angle? Let the acute angles be A and B, with m A = x°. m A + m B = 90° x + m B = 90 m B = (90 – x)° Acute s of rt. are comp. Substitute x for m A. Subtract x from both sides. GEOMETRY
 2 -1 Triangles TEACH! Example 7 c The measure of one of the acute angles in a right triangle is 48 2° What is the measure of. 5 the other acute angle? 2° Let the acute angles be A and B, with m A = 48 5. m A + m B = 90° 2 48 5 + m B = 90 m B = 3° 41 5 Acute s of rt. Substitute 48 Subtract 48 are comp. 2 for m A. 5 2 from both sides. 5 GEOMETRY
2 -1 Triangles TEACH! Example 7 c The measure of one of the acute angles in a right triangle is 48 2° What is the measure of. 5 the other acute angle? 2° Let the acute angles be A and B, with m A = 48 5. m A + m B = 90° 2 48 5 + m B = 90 m B = 3° 41 5 Acute s of rt. Substitute 48 Subtract 48 are comp. 2 for m A. 5 2 from both sides. 5 GEOMETRY
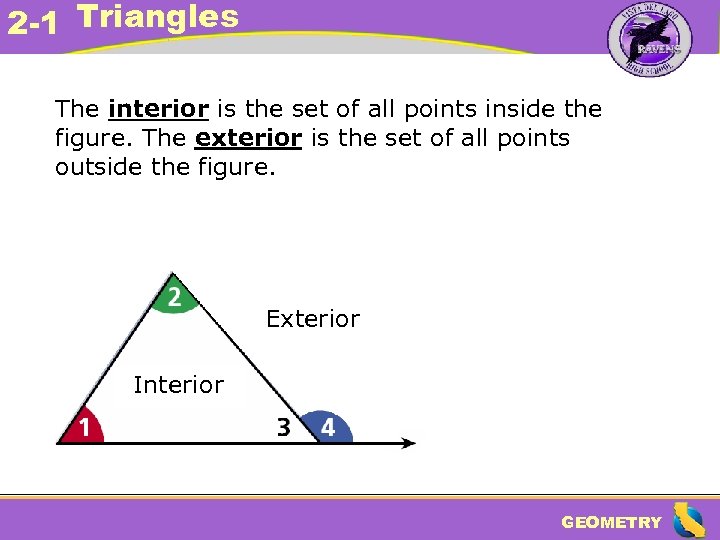 2 -1 Triangles The interior is the set of all points inside the figure. The exterior is the set of all points outside the figure. Exterior Interior GEOMETRY
2 -1 Triangles The interior is the set of all points inside the figure. The exterior is the set of all points outside the figure. Exterior Interior GEOMETRY
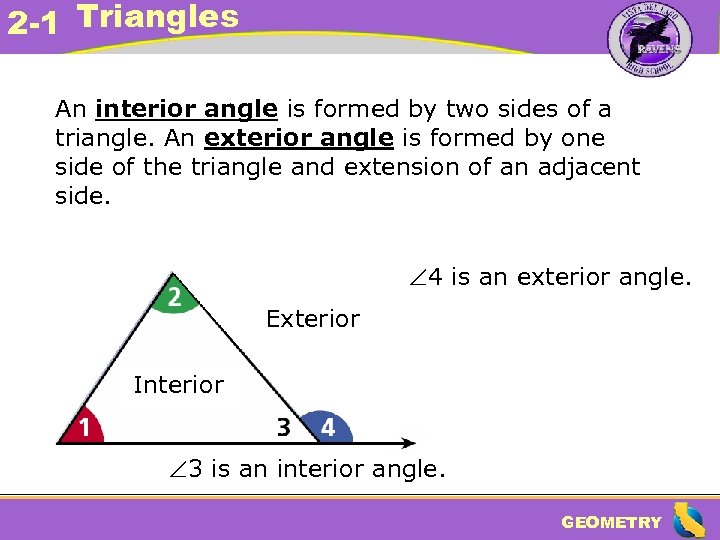 2 -1 Triangles An interior angle is formed by two sides of a triangle. An exterior angle is formed by one side of the triangle and extension of an adjacent side. 4 is an exterior angle. Exterior Interior 3 is an interior angle. GEOMETRY
2 -1 Triangles An interior angle is formed by two sides of a triangle. An exterior angle is formed by one side of the triangle and extension of an adjacent side. 4 is an exterior angle. Exterior Interior 3 is an interior angle. GEOMETRY
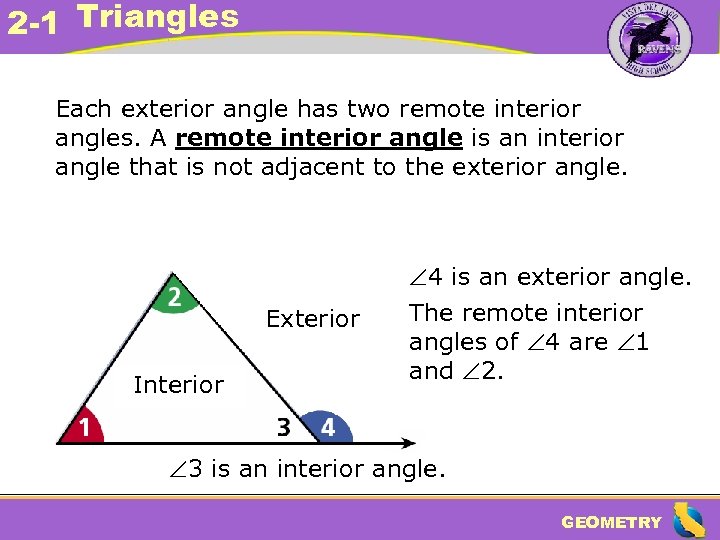 2 -1 Triangles Each exterior angle has two remote interior angles. A remote interior angle is an interior angle that is not adjacent to the exterior angle. 4 is an exterior angle. Exterior Interior The remote interior angles of 4 are 1 and 2. 3 is an interior angle. GEOMETRY
2 -1 Triangles Each exterior angle has two remote interior angles. A remote interior angle is an interior angle that is not adjacent to the exterior angle. 4 is an exterior angle. Exterior Interior The remote interior angles of 4 are 1 and 2. 3 is an interior angle. GEOMETRY
 2 -1 Triangles Corollary: The measure of an exterior angle of a triangle is greater than the measure of either of its remote angles. GEOMETRY
2 -1 Triangles Corollary: The measure of an exterior angle of a triangle is greater than the measure of either of its remote angles. GEOMETRY
 2 -1 Triangles Example 8: Applying the Exterior Angle Theorem Find m B. m A + m B = m BCD Ext. Thm. 15 + 2 x + 3 = 5 x – 60 Substitute 15 for m A, 2 x + 3 for m B, and 5 x – 60 for m BCD. 2 x + 18 = 5 x – 60 78 = 3 x Simplify. Subtract 2 x and add 60 to both sides. Divide by 3. 26 = x m B = 2 x + 3 = 2(26) + 3 = 55° GEOMETRY
2 -1 Triangles Example 8: Applying the Exterior Angle Theorem Find m B. m A + m B = m BCD Ext. Thm. 15 + 2 x + 3 = 5 x – 60 Substitute 15 for m A, 2 x + 3 for m B, and 5 x – 60 for m BCD. 2 x + 18 = 5 x – 60 78 = 3 x Simplify. Subtract 2 x and add 60 to both sides. Divide by 3. 26 = x m B = 2 x + 3 = 2(26) + 3 = 55° GEOMETRY
 2 -1 Triangles TEACH! Example 8 Find m ACD = m A + m B Ext. Thm. 6 z – 9 = 2 z + 1 + 90 Substitute 6 z – 9 for m ACD, 2 z + 1 for m A, and 90 for m B. 6 z – 9 = 2 z + 91 Simplify. 4 z = 100 Subtract 2 z and add 9 to both sides. Divide by 4. z = 25 m ACD = 6 z – 9 = 6(25) – 9 = 141° GEOMETRY
2 -1 Triangles TEACH! Example 8 Find m ACD = m A + m B Ext. Thm. 6 z – 9 = 2 z + 1 + 90 Substitute 6 z – 9 for m ACD, 2 z + 1 for m A, and 90 for m B. 6 z – 9 = 2 z + 91 Simplify. 4 z = 100 Subtract 2 z and add 9 to both sides. Divide by 4. z = 25 m ACD = 6 z – 9 = 6(25) – 9 = 141° GEOMETRY
 2 -1 Triangles GEOMETRY
2 -1 Triangles GEOMETRY
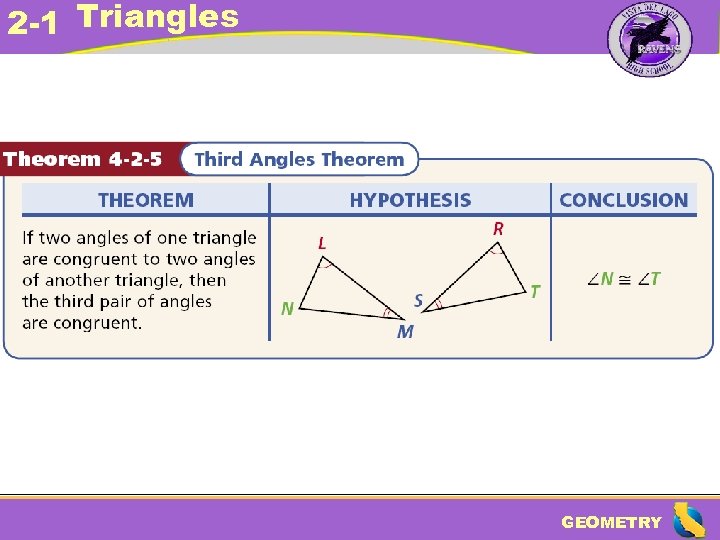
 2 -1 Triangles Example 9: Applying the Third Angles Theorem Find m K and m J. K J m K = m J Third s Thm. Def. of s. 4 y 2 = 6 y 2 – 40 Substitute 4 y 2 for m K and 6 y 2 – 40 for m J. – 2 y 2 = – 40 y 2 = 20 Subtract 6 y 2 from both sides. Divide both sides by -2. So m K = 4 y 2 = 4(20) = 80°. Since m J = m K, m J = 80°. GEOMETRY
2 -1 Triangles Example 9: Applying the Third Angles Theorem Find m K and m J. K J m K = m J Third s Thm. Def. of s. 4 y 2 = 6 y 2 – 40 Substitute 4 y 2 for m K and 6 y 2 – 40 for m J. – 2 y 2 = – 40 y 2 = 20 Subtract 6 y 2 from both sides. Divide both sides by -2. So m K = 4 y 2 = 4(20) = 80°. Since m J = m K, m J = 80°. GEOMETRY
 2 -1 Triangles TEACH! Example 9 Find m P and m T. P T m P = m T Third s Thm. Def. of s. 2 x 2 = 4 x 2 – 32 Substitute 2 x 2 for m P and 4 x 2 – 32 for m T. – 2 x 2 = – 32 x 2 = 16 Subtract 4 x 2 from both sides. Divide both sides by -2. So m P = 2 x 2 = 2(16) = 32°. Since m P = m T, m T = 32°. GEOMETRY
2 -1 Triangles TEACH! Example 9 Find m P and m T. P T m P = m T Third s Thm. Def. of s. 2 x 2 = 4 x 2 – 32 Substitute 2 x 2 for m P and 4 x 2 – 32 for m T. – 2 x 2 = – 32 x 2 = 16 Subtract 4 x 2 from both sides. Divide both sides by -2. So m P = 2 x 2 = 2(16) = 32°. Since m P = m T, m T = 32°. GEOMETRY
 2 -1 Triangles Lesson Quiz: Part I 1. The measure of one of the acute angles in a right triangle is 56 2 °. What is the measure of the other 3 1 acute angle? 33 3 ° 2. Find m ABD. 3. Find m N and m P. 124° 75°; 75° GEOMETRY
2 -1 Triangles Lesson Quiz: Part I 1. The measure of one of the acute angles in a right triangle is 56 2 °. What is the measure of the other 3 1 acute angle? 33 3 ° 2. Find m ABD. 3. Find m N and m P. 124° 75°; 75° GEOMETRY
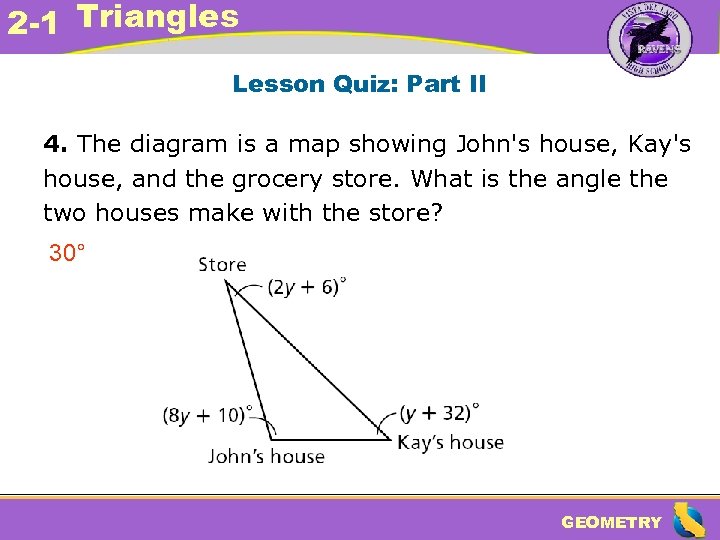 2 -1 Triangles Lesson Quiz: Part II 4. The diagram is a map showing John's house, Kay's house, and the grocery store. What is the angle the two houses make with the store? 30° GEOMETRY
2 -1 Triangles Lesson Quiz: Part II 4. The diagram is a map showing John's house, Kay's house, and the grocery store. What is the angle the two houses make with the store? 30° GEOMETRY


