2 -1 Graphing Quadratic Functions Quadratics Exploration

2 -1 Graphing Quadratic Functions

Quadratics Exploration • Patty paper parabola • Desmos. com – y=ax^2+bx+c add sliders Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 2

• Draw a line (directrix) near the bottom of the pp • Draw a Focus pt. around the center of the line and about 1 in above the line • Make about 12 points approx. equal distance along the directrix • Label each point 1 - ? • Fold pp so that focus pt matches up to each pt drawn on the directrix making a crease each time Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 3

Let a, b, and c be real numbers a 0. The function t f (x) = ax 2 + bx + c esn’ k do m! o is called a quadratic function in standard form. r bo d for u : yo dar te The graph of a quadratic function is a parabola. No this stan call Every parabola is symmetrical about a line called the axis (of symmetry). y The intersection point of the parabola and the axis is called the vertex of the parabola. Copyright © by Houghton Mifflin Company, Inc. All rights reserved. f (x) = ax 2 + bx + c vertex x axis 4

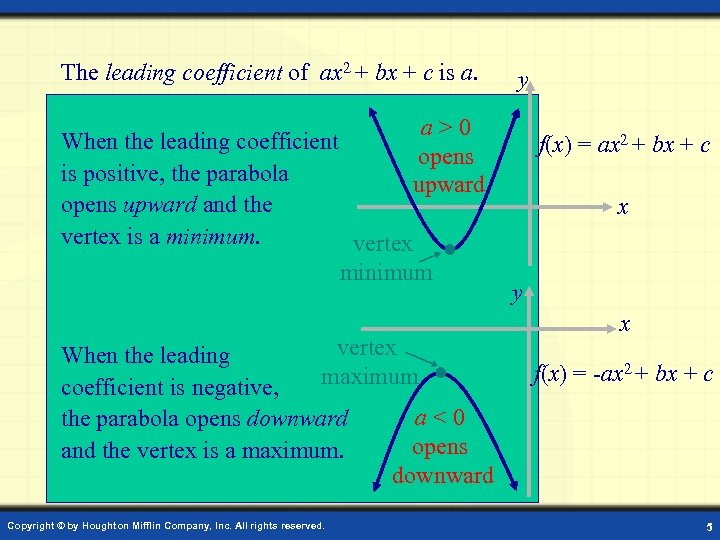The leading coefficient of ax 2 + bx + c is a. y a>0 opens upward When the leading coefficient is positive, the parabola opens upward and the vertex is a minimum. vertex minimum vertex When the leading maximum coefficient is negative, a<0 the parabola opens downward opens and the vertex is a maximum. downward Copyright © by Houghton Mifflin Company, Inc. All rights reserved. f(x) = ax 2 + bx + c x y x f(x) = -ax 2 + bx + c 5

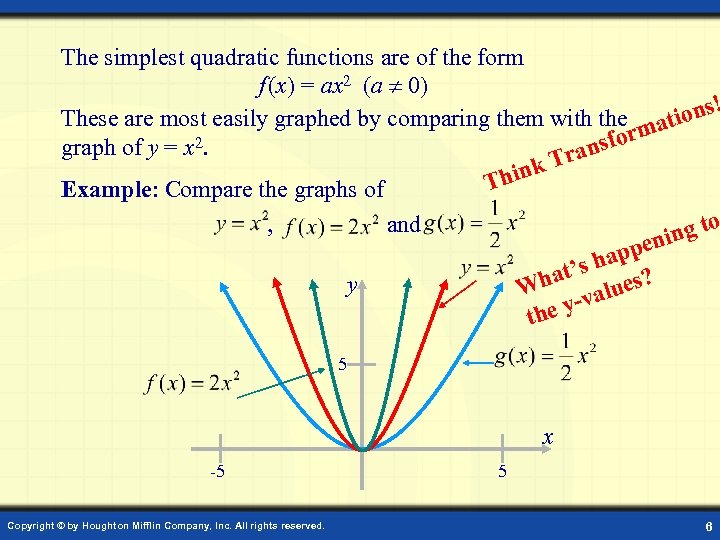The simplest quadratic functions are of the form f (x) = ax 2 (a 0) ons! These are most easily graphed by comparing them with the ati m 2. sfor graph of y = x ran T ink Th Example: Compare the graphs of , o ng t eni and p hap s hat’ lues? W y-va the y 5 x -5 Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 5 6

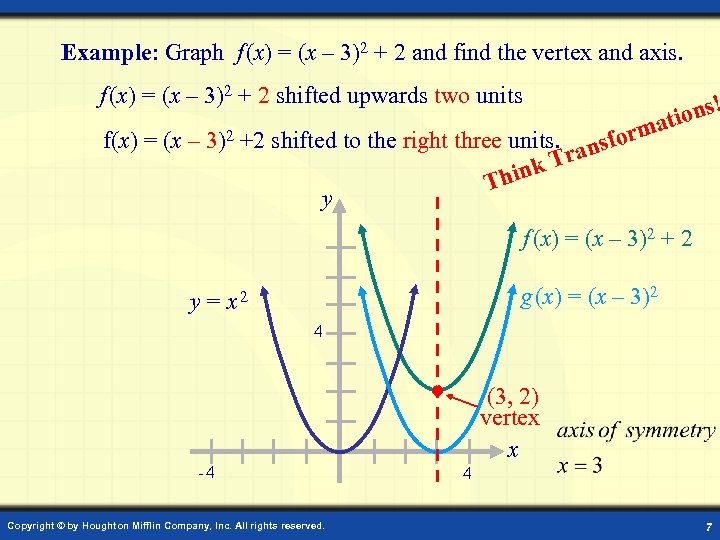Example: Graph f (x) = (x – 3)2 + 2 and find the vertex and axis. f (x) = (x – 3)2 + 2 shifted upwards two units ons! ati f(x) = (x – 3)2 +2 shifted to the right three units. ansform k Tr Thin y f (x) = (x – 3)2 + 2 g (x) = (x – 3)2 y = x 2 4 -4 Copyright © by Houghton Mifflin Company, Inc. All rights reserved. (3, 2) vertex x 4 7

The vertex form for the equation of a quadratic function is: f (x) = a(x – h)2 + k (a 0) The graph is a parabola opening upward if a 0 and opening downward if a 0. The axis is x = h, and the vertex is (h, k). s s thi call k boo r you rm! ote: d fo N r nda sta Vertex form can be extremely helpful when graphing quadratics as it tells you the axis of symmetry, vertex and direction Additional information needed is x and y intercepts or points. Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 8

The vertex form for the equation of a quadratic function is: f (x) = a(x – h)2 + k (a 0) The graph is a parabola opening upward if a 0 and opening downward if a 0. The axis is x = h, and the vertex is (h, k). Example: Graph the parabola f (x) = 2 x 2 + 4 x – 1 and find the axis y and vertex. Use vertex form. 2 f (x) = 2 x + 4 x – 1 f (x) = 2 x 2 + 4 x – 1 original equation f (x) = 2( x 2 + 2 x) – 1 factor out 2 f (x) = 2( x 2 + 2 x + 1) – 1 – 2 complete the square f (x) = 2( x + 1)2 – 3 vertex form x Intercepts? a > 0 parabola opens upward like y = 2 x 2. h = – 1, k = – 3 axis x = – 1, vertex (– 1, – 3). Copyright © by Houghton Mifflin Company, Inc. All rights reserved. x = – 1 (– 1, – 3) 9

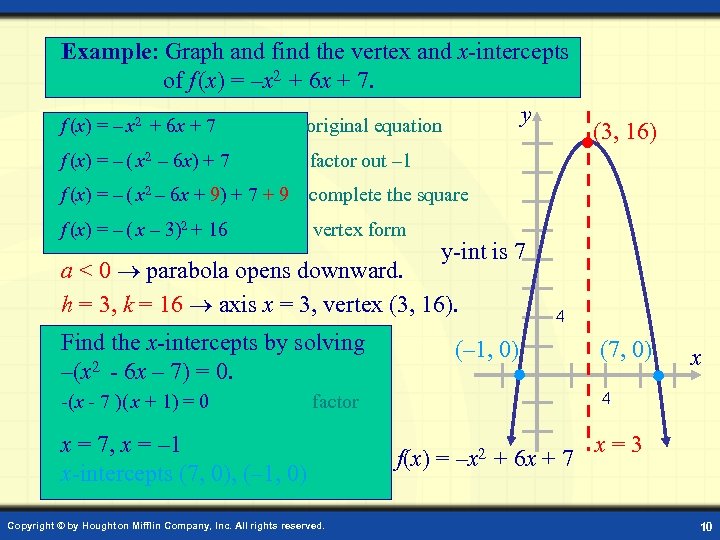Example: Graph and find the vertex and x-intercepts of f (x) = –x 2 + 6 x + 7. y f (x) = – x 2 + 6 x + 7 original equation f (x) = – ( x 2 – 6 x) + 7 factor out – 1 f (x) = – ( x 2 – 6 x + 9) + 7 + 9 complete the square f (x) = – ( x – 3)2 + 16 vertex form (3, 16) y-int is 7 a < 0 parabola opens downward. h = 3, k = 16 axis x = 3, vertex (3, 16). Find the x-intercepts by solving –(x 2 - 6 x – 7) = 0. -(x - 7 )( x + 1) = 0 4 (– 1, 0) Copyright © by Houghton Mifflin Company, Inc. All rights reserved. x 4 factor x = 7, x = – 1 x-intercepts (7, 0), (– 1, 0) (7, 0) f(x) = –x 2 + 6 x + 7 x=3 10

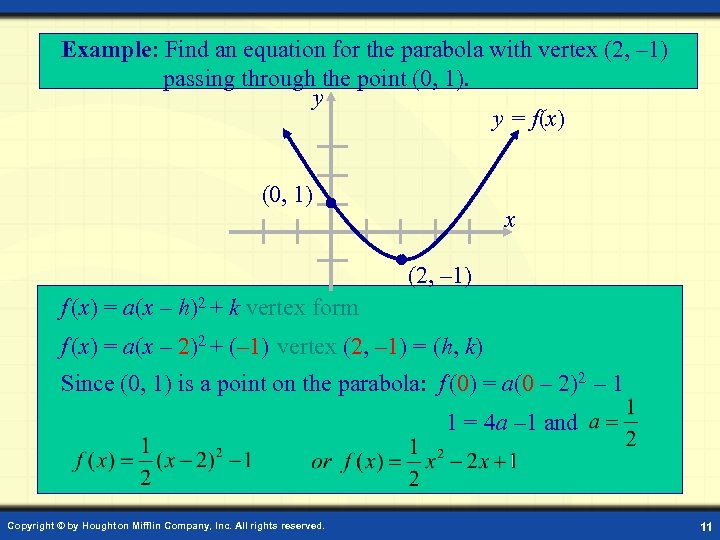Example: Find an equation for the parabola with vertex (2, – 1) passing through the point (0, 1). y y = f(x) (0, 1) x (2, – 1) f (x) = a(x – h)2 + k vertex form f (x) = a(x – 2)2 + (– 1) vertex (2, – 1) = (h, k) Since (0, 1) is a point on the parabola: f (0) = a(0 – 2)2 – 1 1 = 4 a – 1 and Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 11

We can find the vertex of a parabola in standard form as well. The vertex of the graph of f (x) = ax 2 + bx + c (a 0) Example: Find the vertex of the graph of f (x) = x 2 – 10 x + 22 original equation a = 1, b = – 10, c = 22 At the vertex, So, the vertex is (5, -3). Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 12

Example: A basketball is thrown from the free throw line from a height of six feet. What is the maximum height of the ball if the path of the ball is: The path is a parabola opening downward. The maximum height occurs at the vertex. At the vertex, So, the vertex is (9, 15). The maximum height of the ball is 15 feet. Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 13

Example: A fence is to be built to form a rectangular chicken coop along the side of a house. If 120 feet of fencing are available, what are the dimensions of the corral of maximum area? house coop If I use all 120 ft. of fencing with different dimensions, will I always get the same area? Find the areas: barn 1 corral barn 1 118 Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 50 corral 50 20 14

Example: A fence is to be built to form a rectangular chicken coop along the side of a house. If 120 feet of fencing are available, what are the dimensions of the corral of maximum area? house x coop x 120 – 2 x Let x represent the width of the coop and 120 – 2 x the length. Area = A(x) = (120 – 2 x) x = – 2 x 2 + 120 x The graph is a parabola and opens downward. The maximum occurs at the vertex where a = – 2 and b = 120 – 2 x = 120 – 2(30) = 60 The maximum area occurs when the width is 30 feet and the length is 60 feet. Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 15

• Juggling Activity! Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 16

H Dub • 2 -1 Page 134 #1 -8 all, 13 -27 EOO, 37 -47 odd, 75, 76, 78 Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 17

Quadratics Exploration • http: //www. mathsisfun. com/algebra/quadrat ic-equation-graph. html • Or • Desmos. com – y=ax^2+bx+c add sliders Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 18