2 -1 Functions What is a Function

2 -1 Functions

What is a Function? Definition: _______________________________ The x values of a function are called the __________ and all the y values are called the __________________________ X is called the “___________” while y is the “___________”

Well, what would a non function look like? Equations that would not be functions: • _____________________________________________________

Domain? What was that? -the x values. The easiest way to define the domain _________________________________________ a) ___________________ b) __________________ Either is acceptable.

Examples: Find the Domain of each

Function Notation The algebraic expression is a function. There are LOTS of functions out there (any equation you can dream up where an x will produce only one y value is a function) but I am going to use this one for now. To show that something IS a function, it is written like this: Don’t worry! __________________________________

OK – how do we use it? Lets use the sample from before. 1. Given find f(1), f(-2) and f(0). The function is simply an instruction of what to do to x. __________________ Plug 1 in for all x’s and solve for y and put as a ordered pair (x, y) f(1)= f(-2)= f(0)=

Examples Find the domain of 3. 4. 5.

2. 2 Graphing Lines Going from an equation to a picture

What methods can I use to graph line? 1. ___________________________ ______________ Please graph 2 x + 3 y = 6

What method can I use to graph line? 2. _____________________________ Lets review slope for a minute

SLOPE 1. Slope = Please graph y = -3 x +4

Special Things Parallel Lines Perpendicular Lines Horizontal Lines Vertical Lines

Other Review Items ____________

2. 3 Equations of Lines Going the other direction – from a picture to the equation

There are 3 standard forms of equations 1. Slope intercept form _______ 2. Standard form _____________________ 3. Point slope form

So, what do you need to have to find the equation of the line? Lets try one: Slope=2 and the y-int = 5

1. Convert y = 1. 5 x – 6 to standard form. • __________________________________ 2. Convert 10 x – 2 y = 3 to slope/intercept

Find the equation of the line that has Slope = 3, y intercept = 10 Slope = 3, x intercept = 10 Slope = 3, passes through (10, 10)

6. Parallel to -4 x + 2 y = 10 and passes through (-1, -1) 1. 7. Parallel to x + 2 y = 1 and passes through the point of intersection of the lines y = 3 x – 2 and y = 2 x + 1.

Triangle ABC has vertices A(-4, -2) L(2, 8) G(6, 2) • Write the equation of AL

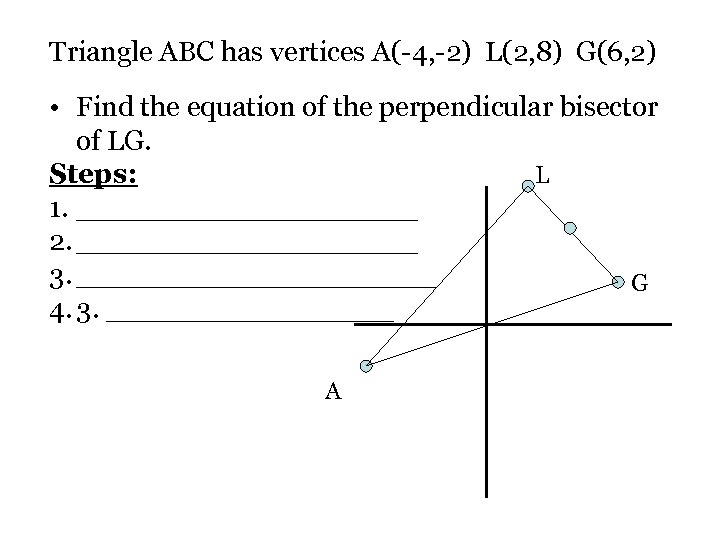Triangle ABC has vertices A(-4, -2) L(2, 8) G(6, 2) • Find the equation of the perpendicular bisector of LG. L Steps: 1. __________ 2. __________ 3. __________ G 4. 3. ________ A

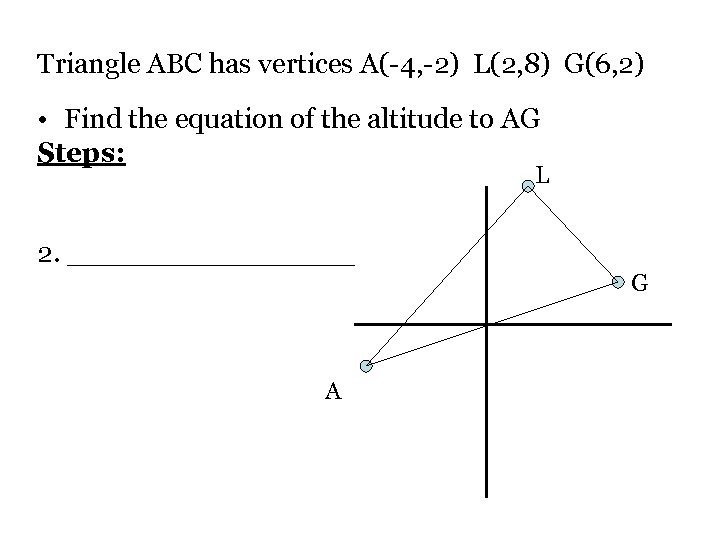Triangle ABC has vertices A(-4, -2) L(2, 8) G(6, 2) • Find the equation of the altitude to AG Steps: L 2. ________ G A

2 -4 A Variety of Graphs Piecewise Functions

What are Piecewise Functions? Piecewise functions are defined ___________________________________

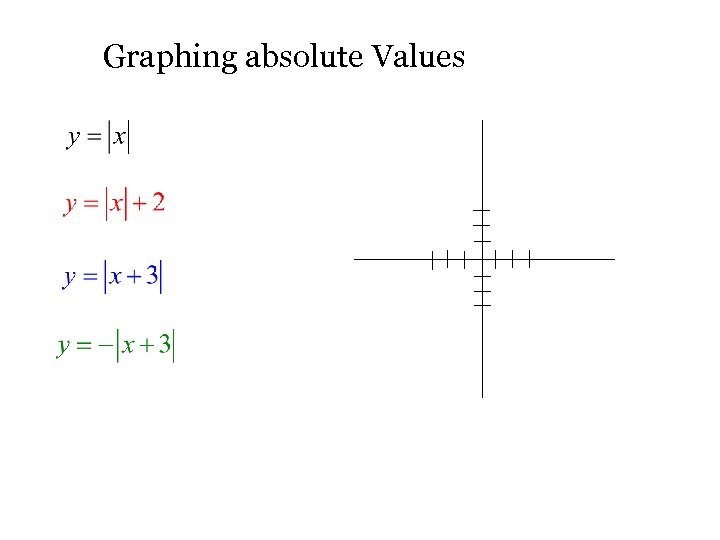Graphing absolute Values

How will we graph? ______________________________ _______________

Graphing Absolute Value 1. __________________________________________ 2. _________________________________________

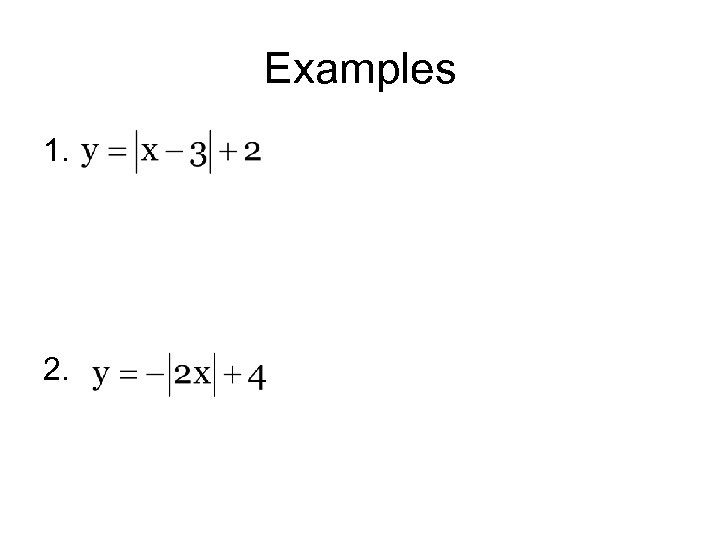Examples 1. 2.

The next kind of piecewise function The form of this function is similar to this: This looks worse than it is. Essentially the function is split into multiple functions based on particular domains. ___________________________________

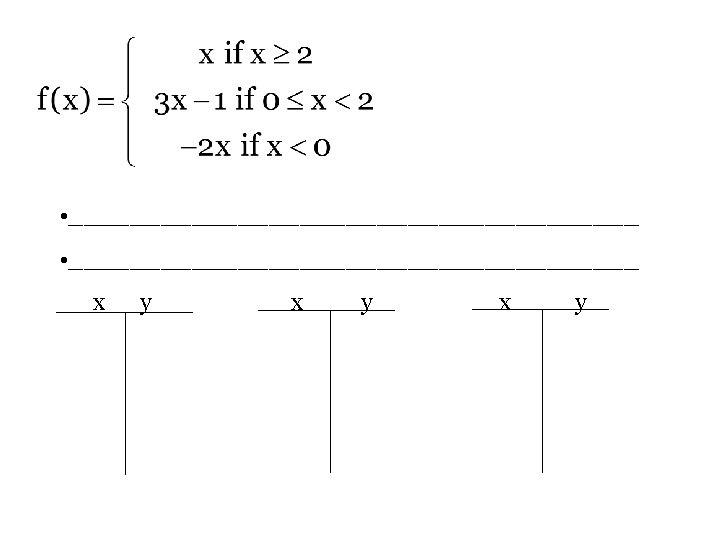• _____________________________________ x y x y

2 -5 Systems of Equations Finding a solution that works for multiple equations

Warm Up Please graph on one set of axes the following:

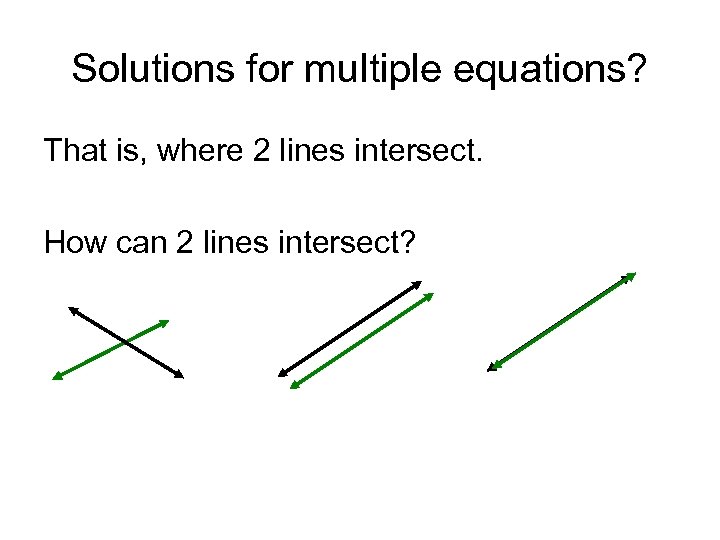Solutions for multiple equations? That is, where 2 lines intersect. How can 2 lines intersect?

What methods have you already learned for finding where 2 line intersect? 1. ____________________ 2. __________________________________________ 3. __________________________________________

What method do you have to use? Unless specified (i. e. follow directions) you may use ANY method you want. I want you to be happy. Examples:

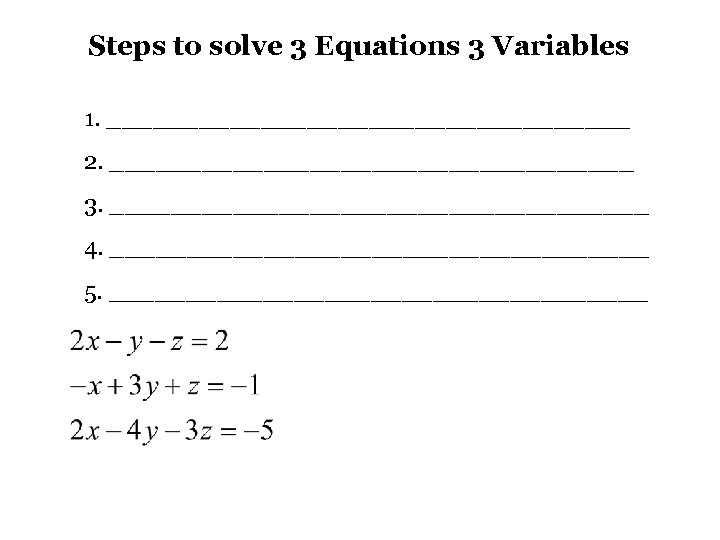Steps to solve 3 Equations 3 Variables 1. _________________ 2. _________________ 3. __________________ 4. __________________ 5. __________________

1. A golfer scored only 4’s and 5’s in a round of 18 holes. His score was 80. How many of each score did he have?

2. Tuition plus Room/Board at a local college is $24, 000. Room/Board is $400 more than onethird the tuition. Find the tuition.

3. Mr. Tem bought 7 different shirts for the coaches of his baseball team. The blue long sleeved shirts cost $30 each and the white short sleeved shorts cost $20 each. If he paid a total of $160, how many of each shirt did he buy? ?

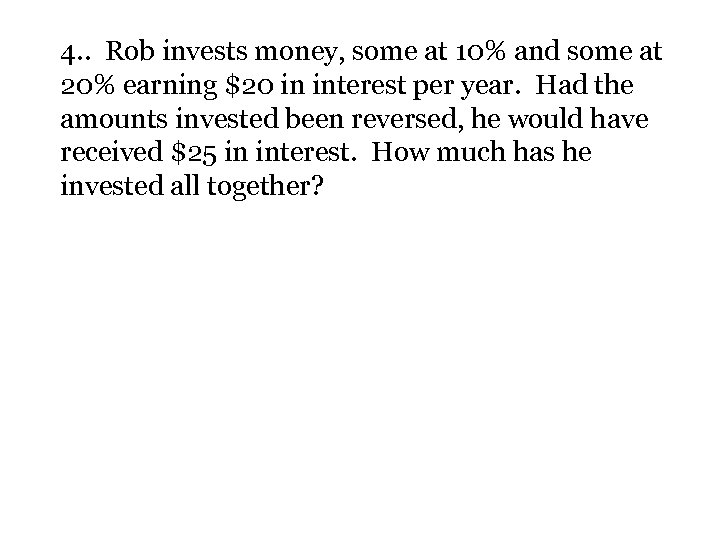4. . Rob invests money, some at 10% and some at 20% earning $20 in interest per year. Had the amounts invested been reversed, he would have received $25 in interest. How much has he invested all together?

6. The sum of two numbers is 20. The larger is 5 less than twice the smaller. What are the numbers? ?

2 -6 Graphing Quadratic Functions

No more linear functions What happens graphically when an equation’s high power is 2? _____________________________

The Parabola (The Picture)

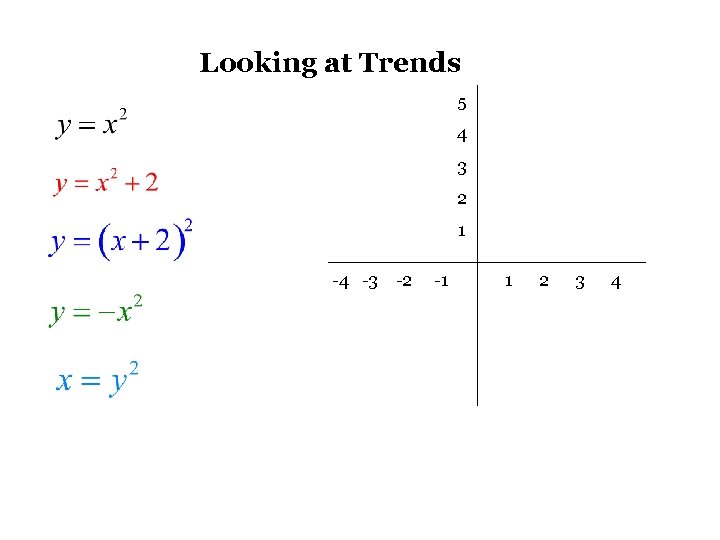Looking at Trends 5 4 3 2 1 -4 -3 -2 -1 1 2 3 4

So, we see some trends We probably won’t use trends; much like absolute values, one easy way to graph parabolic functions is to plot the vertex and then plot 2 points on either side of the x coordinate of the vertex.

The Parabola (The Equation) From what we saw, these are the trends: Add/Subtract inside the squared quantity? ____________ Add/Subtract outside the squared quantity? ____________ Multiply/Divide inside or outside? ____________

The Parabola (The Equation) a ______________ (h, k) _____________ If a < 0, what will happen to the graph?

So what will we do with this information? 1. Determine the vertex (h, k). 2. Find 1 x values on either side of h and plug them in to find 2 points to graph. 3. If asked to, determine domain (hint what CAN’T you put in? ) 4. If asked to, determine range (hint – decide up/down orientation then think about where you will move from the vertex).

Examples: 4 1

4 2

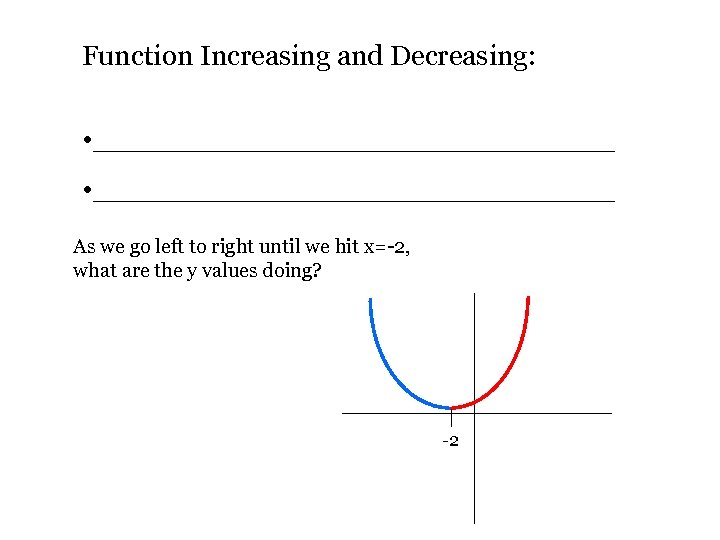Function Increasing and Decreasing: • _____________________________ As we go left to right until we hit x=-2, what are the y values doing? -2

2 -7 The Quadratic Formula and Completing the Square Day 1 Completing the Square

When the directions are “graph” In the last section the graphs were already in parabolic form, which makes graphing easy. The vertex is right there to see. What if instead you are asked to graph _________________ How would we go about graphing this one? By just plotting points, will we be able to find the vertex easily? Not necessarily…

Completing the Square Completing the square is the way to convert a parabola in “quadratic form” to “parabolic form” so that you can find the vertex easily. ______________________________

Completing the Square In this method you “complete the square” by adding the same thing to both sides of an equation so as to create a perfect square trinomial. Then by factoring and isolating f(x), you will have parabolic form. Easier than it sounds… with a little review

Perfect Square Trinomials Is there a relationship between the red term and the blue term?

This is what you will add to both sides of a quadratic equation. _______________ This will create a factorable perfect square trinomial. Then, depending on whether you want to solve or graph you go from there. We’ll do an example of each to see both paths.

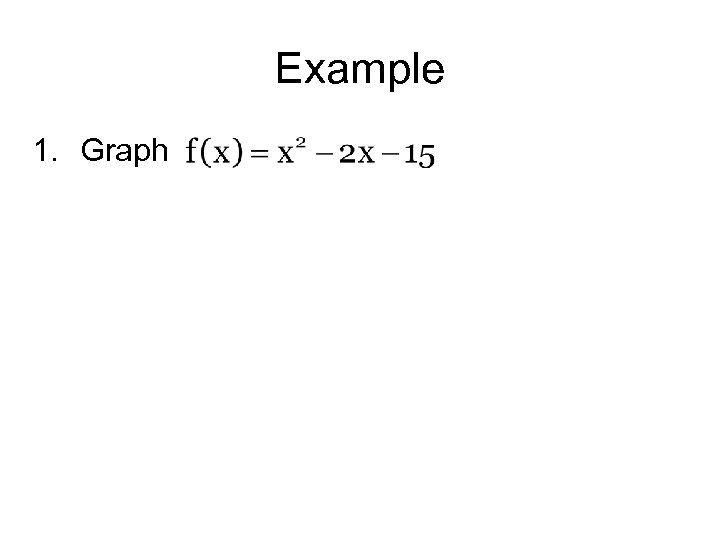Example 1. Graph

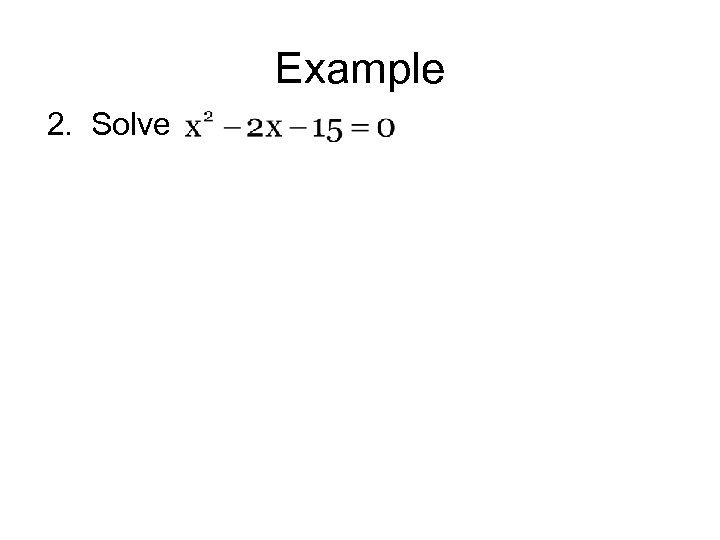Example 2. Solve

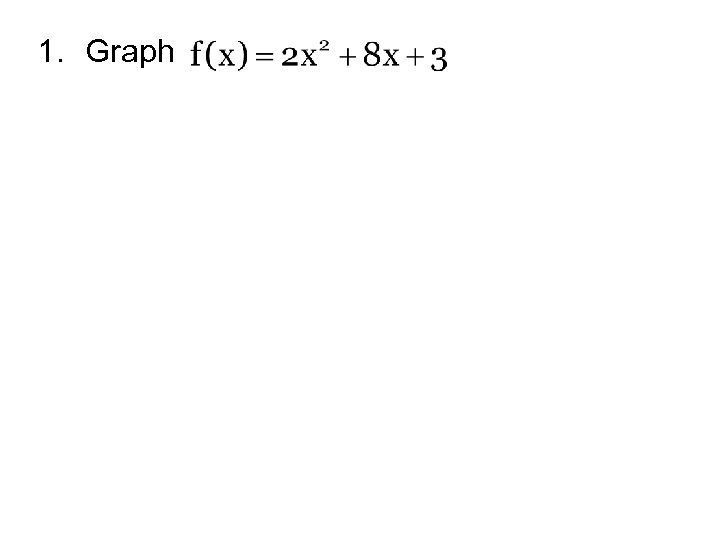1. Graph

Using Completing the square: • _________________________________

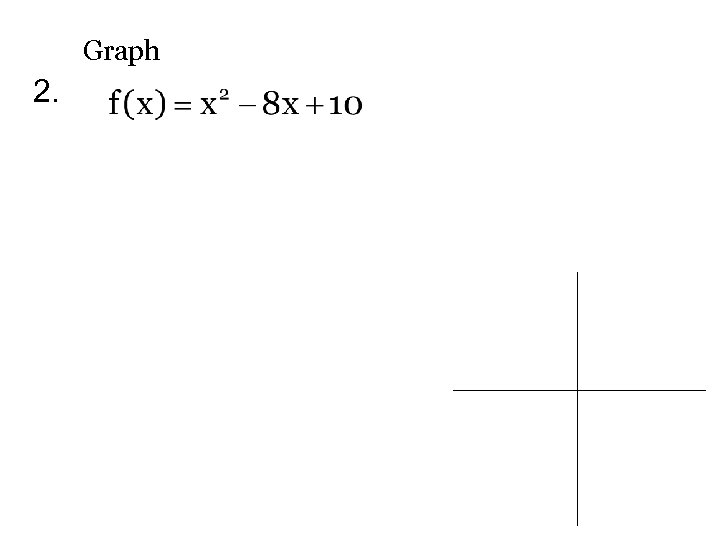Graph 2.

Solve by completing the square

2 -7 The Quadratic Formula and Completing the Square The Quadratic Formula

Quadratic Equation The numbers for the variables come from:

The Discriminant ______________________________ ___________________

Example

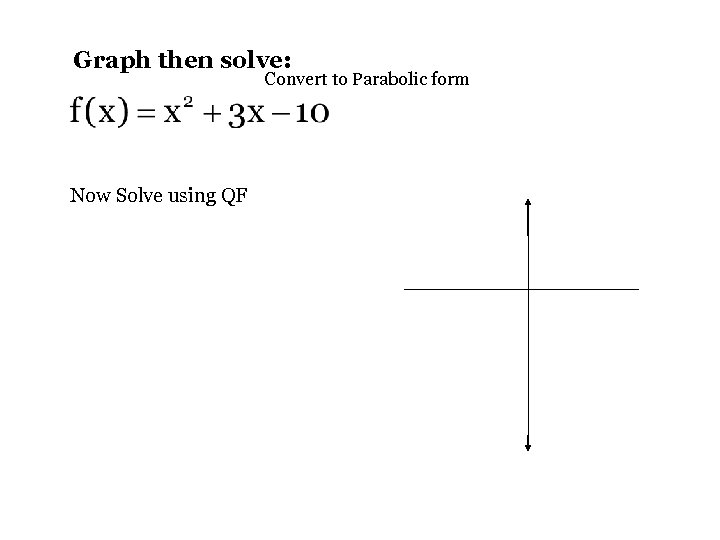Graph then solve: Convert to Parabolic form Now Solve using QF

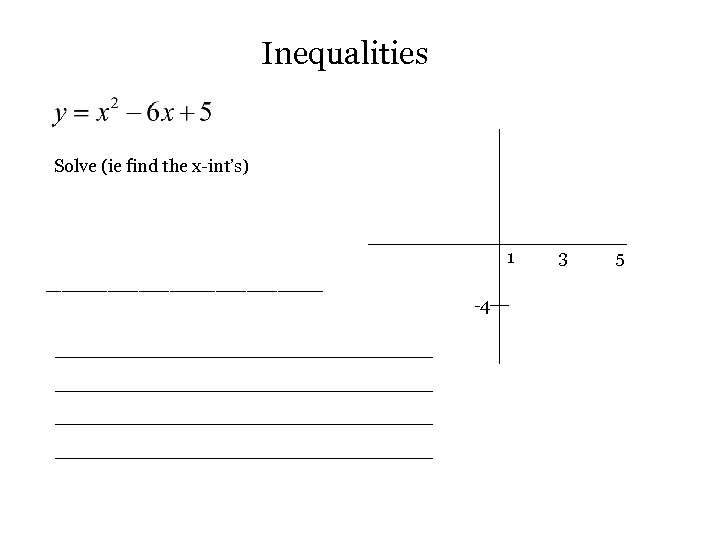Inequalities Solve (ie find the x-int’s) 1 _________ -4 _____________________ 3 5

Easy Way to solve Inequalities • ______________________________ • _______________

2. 8 Quadratic Applications Word Problems

In the Word Problems Essentially you will see three things. 1. ________________ 2. ________________________________ ________ 3. ________________________________

Maximize? Minimize Why would we be talking about maximizing or minimizing with quadratic word problems? _______________

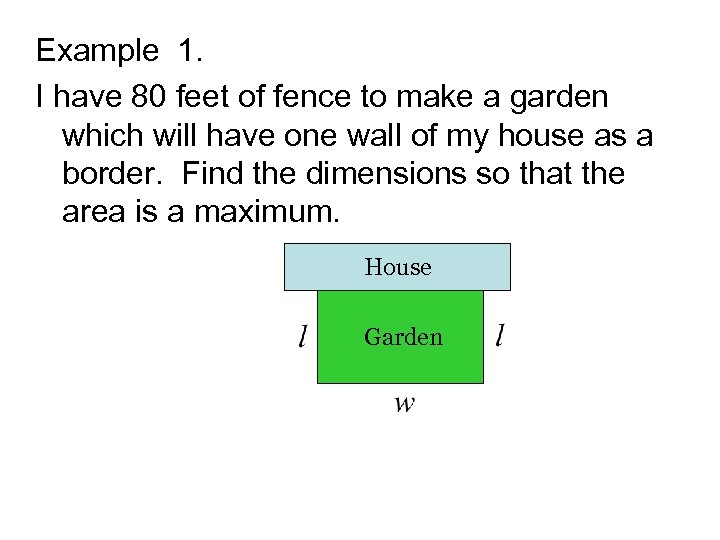Example 1. I have 80 feet of fence to make a garden which will have one wall of my house as a border. Find the dimensions so that the area is a maximum. House Garden

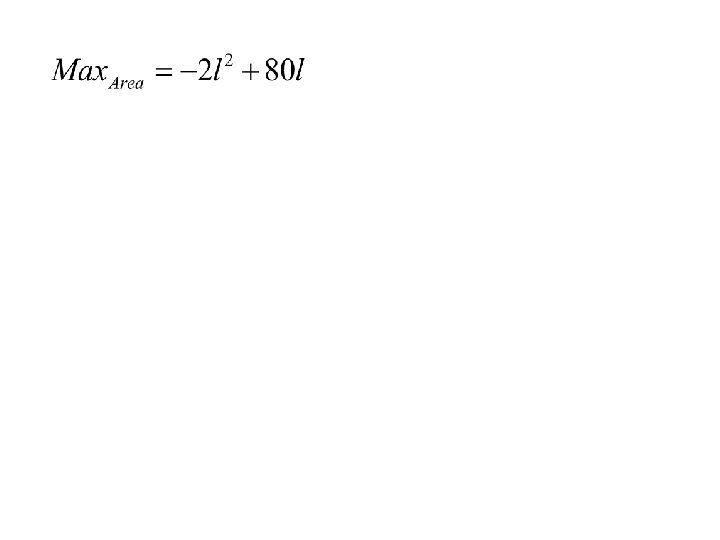
2. The sum of two numbers is 40. Find the two numbers if their product is a maximum.

2. Find two consecutive positive integers such that the sum of their squares is 113. (notice! No “maximum/minimum”)

The sum of a number and its square is 72. Find the number

The sum of 2 numbers is 12. Find the numbers if the product of one and twice the other is a maximum.