19 Магнитное поле в веществе Намагниченность До сих

19. Магнитное поле в веществе. Намагниченность. До сих пор считалось, что проводники находятся в вакууме. Если токи находятся в среде, то магнитное поле меняется. Это связано с тем, что всякое вещество является магнетиком, то есть оно способно под действием внешнего магнитного поля В 0, созданного токами текущими по проводникам (макротоками), приобретать магнитный момент (намагничиваться). В результате вещество создает дополнительное магнитное поле В´, которое В 0. В = В 0 + В´ накладывается на внешнее поле магнитное поле равно Результирующее (42)

Магнитное поле В называется микроскопическим магнитным полем – оно сильно меняется на межатомных расстояниях. Однако, при макроскопическом рассмотрении оно не обнаруживается. Поэтому, как и в случае электрического поля, в качестве характеристики магнитного поля в веществе используют усредненное по физически бесконечно малому объему значение поля. Далее будем считать, что в формуле (41) присутствуют именно усредненные макроскопические поля.

Поле В´, как и поле В 0, не имеет источников, поэтому дивергенция результирующего поля В равна нулю Следовательно, теорема Гаусса справедлива не только для магнитного поля в вакууме, но и для суммарного магнитного поля в веществе

Для объяснения намагничивания тел Ампер предположил, что в атомах и молекулах циркулируют круговые токи, обусловленные движением электронов. Эти токи создают вокруг себя магнитное поле. В отсутствие внешнего поля молекулярные токи ориентированы беспорядочно. Поэтому созданное всеми молекулами и атомами вещества магнитное поле и магнитный момент равны нулю. Под действием внешнего магнитного поля В 0 магнитные моменты молекул поворачиваются и приобретают преимущественную ориентацию, в результате чего вещество намагничивается – возникает дополнительное магнитное поле В´, а суммарный магнитный момент всех молекул становится отличным от нуля.

Для описания намагничивания веществ используют магнитный момент единицы объема - эту величину называют намагниченностью. Она является аналогом поляризованности. Намагниченность вещества в некоторой его точке определяется выражением (43) где V - физически бесконечно малый объем в окрестности рассматриваемой точки, – вектор магнитного момента отдельной молекулы. Суммирование ведется по всем молекулам, находящимся внутри объема V.

20. Напряженность магнитного поля. Применим операцию ротор к уравнению (42) Ранее было получено где - плотность макроскопического тока. Аналогичная формула имеет место и для вектора где - плотность молекулярных токов.

Поэтому ротор результирующего магнитного поля в веществе можно записать в виде (44) Плотность молекулярных токов зависит от магнитного поля В. Поэтому для определения нужно знать плотность не только макроскопических, но и молекулярных токов, что создает определенное затруднение. Найдем величину, которая определяется только макроскопическими токами. Для этого сначала выразим плотность молекулярных токов через намагниченность.

Рассмотрим некоторый замкнутый контур Г внутри вещества. Сумма молекулярных токов, текущих через него, равна где S – поверхность, натянутая на контур Г. В интеграл вклад дают лишь те молекулярные токи Iмол, которые нанизаны на контур и пересекают поверхность S один раз. Пусть dl – элемент контура, образующий с намагниченностью угол . Этот элемент пронизывает молекулярные токи, центры которых находятся внутри косого цилиндра.

Объем цилиндра равен где - площадь, охватываемая одним молекулярным током. Пусть n - концентрация молекул, тогда полный ток, охватываемый элементом контура dl равен здесь произведение - есть магнитный момент одного молекулярного тока pm. Поэтому - есть дипольный момент единицы объема, равный модулю вектора намагниченности.

Величина - есть проекция вектора на направление элемента контура dl. Поэтому молекулярный ток, охватываемый элементом dl, можно записать как. Тогда сумма молекулярных токов, охватываемых всем контуром Г есть Преобразуем правый интеграл с помощью теоремы Стокса

Полученное равенство должно выполняться при произвольном выборе поверхности S, что возможно, лишь если равны подинтегральные функции (45) Таким образом, плотность молекулярных токов равна ротору намагниченности.

Подставим (45) в (44) Что можно переписать в виде (46) Отсюда следует, что вектор (47) определяется лишь макроскопическими токами. Вектор называется напряженностью магнитного поля. Он и есть искомая нами величина и характеризует магнитное поле макротоков.

Подставляя (47) в (46) , получаем (48) Ротор напряженности магнитного поля равен вектору плотности макроскопических токов. Возьмем поверхностный интеграл от обеих частей уравнения (48) по поверхности S, натянутой на замкнутый контур Г Согласно теореме переписать в виде Стокса левый интеграл можно

Следовательно (49) Если макроскопические токи текут по проводам, охватываемым контуром, то (49) можно переписать в виде (50) Формулы (49) и (50) выражают теорему о циркуляции вектора : циркуляция вектора напряженности магнитного поля по некоторому контуру равна алгебраической сумме макроскопических токов, охватываемых этим контуром.

Напряженность магнитного поля аналогом электрического смещения является. Намагниченность вакуума равна нулю , поэтому напряженность магнитного поля в вакууме равна В частности, для прямого тока магнитная индукция , а напряженность Отсюда следует размерность напряженности Согласно (47) такую же размерность имеет и намагниченность. .

Опыт показывает, что в не сильных магнитных полях намагниченность пропорциональна напряженности магнитного поля (51) где - магнитная безразмерная величина. восприимчивость магнетика,

Подставим (51) в (47) Откуда (52) Величина, равная (53) называется магнитной проницаемостью вещества. Она показывает во сколько раз магнитное поле макротоков Н

Теперь формулу (52) можно переписать в виде (54) В анизотропных средах направления векторов В и Н могут не совпадать.

21. Условия на границе раздела двух магнетиков. Пусть имеются два однородных магнетика с магнитными проницаемостями 1 и 2. Найдем связь векторов В и Н в двух средах на границе их раздела. Построим вблизи границы цилиндр с высотой h и основаниями S. Внешние нормали n и n´ к основаниям направлены в противоположные стороны.

Согласно теореме Гаусса поток магнитной индукции ФВ через замкнутую поверхность цилиндра равен нулю (55) С другой стороны расписать как поверхностный интеграл можно Устремляя высоту цилиндра к нулю h 0, потоком через боковую поверхность можно пренебречь. Тогда с учетом (55) получаем

Если проецировать вектора индукции В 1 и В 2 на одну и ту же нормаль (например n), то (56) Используя (54) можем переписать (56) в виде или (57)

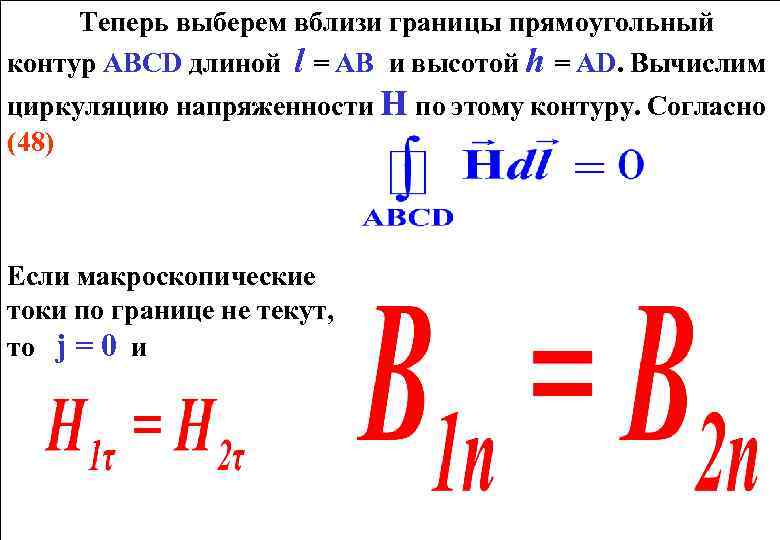Теперь выберем вблизи границы прямоугольный контур АВCD длиной l = АВ и высотой h = AD. Вычислим циркуляцию напряженности Н по этому контуру. Согласно (48) Если макроскопические токи по границе не текут, то j = 0 и

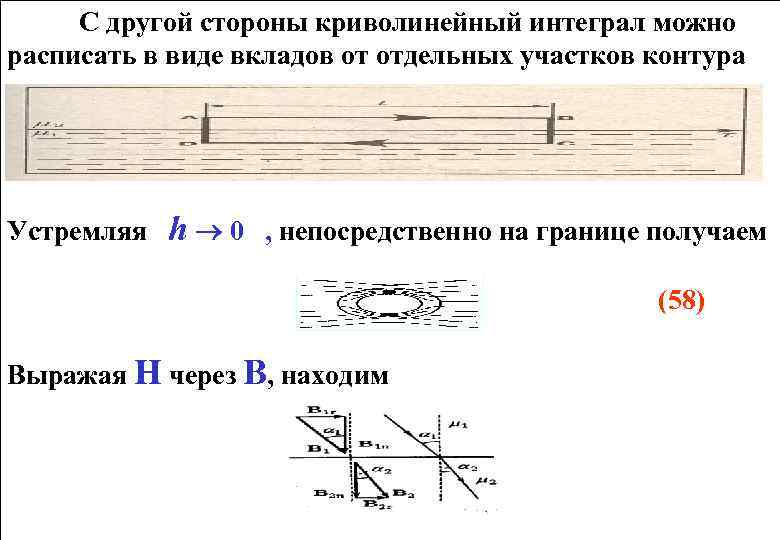С другой стороны криволинейный интеграл можно расписать в виде вкладов от отдельных участков контура Устремляя h 0 , непосредственно на границе получаем (58) Выражая Н через В, находим

Откуда (59) Таким образом, из формул (56 -59) следует, что при переходе через границу раздела двух магнетиков нормальная составляющая вектора магнитной индукции В (Вn) и тангенциальная составляющая вектора напряженности магнитного поля Н (Н ) непрерывны, тогда как тангенциальная составляющая вектора В (В ) и нормальная составляющая вектора Н (Нn) терпят скачок.

Рассмотрим поведение линий магнитной индукции при пересечении границы. Из рисунка следует, что С учетом (56) и (59) получаем (60) закон преломления магнитной индукции.

Из закона преломления следует, что при переходе в магнетик с большей магнитной проницаемостью линии индукции отклоняются от нормали, что приводит к их сгущению. Это используется для магнитной защиты приборов. Для этого приборы окружают железным экраном, в толщине которого происходит сгущение линий магнитной индукции, что приводит к ослаблению магнитного поля внутри экрана.

22. Виды магнетиков Формула (51) определяет магнитную восприимчивость единицы объема вещества. Часто используют восприимчивость, отнесенную к одному молю вещества. Они связаны между собой формулой где Vm – молярный объем. Поэтому, в то время как величина безразмерная, - имеет размерность -

В зависимости от знака и величины магнитной восприимчивости все магнетики делят на 3 группы: 1) диамагнетики – у которых абсолютной величине отрицательная и мала по 2) парамангетики – у которых мала по величине положительная, но тоже 3) ферромагнетики – у которых большая по величине положительная и очень

У диамагнетиков и парамагнетиков восприимчивость не зависит от напряженности магнитного поля. В отличие от них у ферромагнетиков магнитная восприимчивость является функцией от напряженности магнитного поля. У парамагнетиков и ферромагнетиков намагниченность J совпадает по направлению с напряженностью Н. У диамагнетиков вектора J и Н направлены в противоположные стороны.