17 11 16 Синус косинус и тангенс для

17. 11. 16 Синус, косинус и тангенс для угла от 0° до 180°

Повторим про синус, косинус, тангенс. Решите задачи

1. Начертим в прямоугольной системе координат единичную полуокружность, радиус ОА=ОС=ОВ=1 2. Выберем точку М на окружности в 1 четверти, ее координаты М (х; у) 4. Тогда длины отрезков ОД=х, ДМ=у, ОМ=1. 4. Проведем перпендикуляр из точки М на ось Ох. 5. Найдите синус и косинус угла полученные равенства , запишите

Проверим Подставьте в эти равенства ОД=х, МД =у, ОМ=1. Какие получатся новые равенства?

Проверим

Установим границы для синуса и косинуса O Так как по рисунку

Радиус Какую полуокружность называют единичной? равен 1, центр в начале координат, расположена в 1 и 2 координатной четверти.

Что называют синусом угла α, называется ордината точки Синусом углагде 0°≤α≤ 180° sin α = y Что называют косинусом угла α, где 0°≤α≤ 180° Косинусом угла называется абсцисса точки cos α = x

В каких пределах находится значение синуса, косинуса?

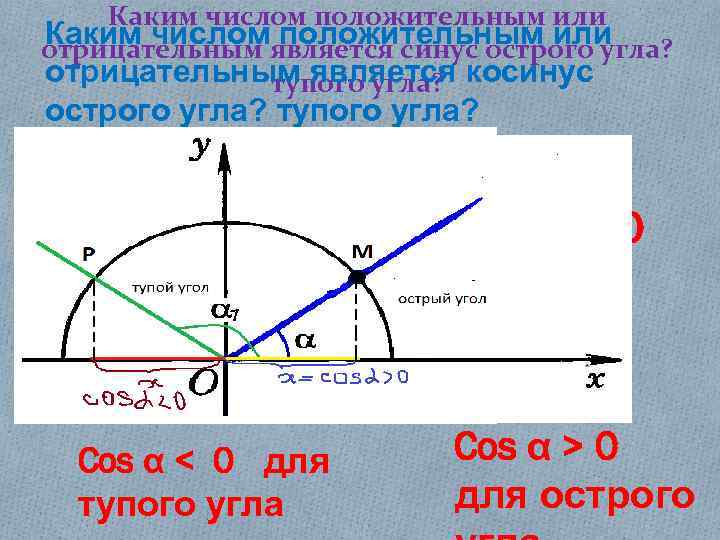Каким числом положительным или Каким числомявляется синус острого угла? положительным или отрицательным является косинус тупого угла? острого угла? тупого угла? Sinα≥ 0 Cos α < 0 для тупого угла Cos α > 0 для острого

Какой формулой связаны синус и косинус одного и того же угла? Основное тригонометрическое тождество

Что называют тангенсом угла α, где 0°≤α≤ 180° Тангенс – это отношение синуса к косинусу этого же угла(α≠ 90°)

Почему тангенс не определен для угла 90°? х = cosα ≠ 0 значит α≠ 90°

Леонард Эйлер ввел и само понятие функции и принятую в наши дни символику. Он придал всей тригонометрии ее современный вид.