16 3 Расчет элементов конструкций при ударном нагружении

16. 3. Расчет элементов конструкций при ударном нагружении Под ударом понимается соприкосновение двух движущихся тел, в результате которого их скорости изменяются за очень короткий период времени. Время удара исчисляется тысячными, а иногда и миллионными долями секунды. Скорость ударяющего тела практически мгновенно изменяется (уменьшается зачастую до нуля), поэтому на тело, воспринимающее удар (ударяемое тело), передаются очень большие ускорения. Эти ускорения остаются неизвестными, так как точное время удара мы не знаем. При ударе происходит очень быстрое превращение одного вида энергии в другой: кинетическая энергия ударяющего тела превращается в потенциальную энергию деформации ударяемого тела.

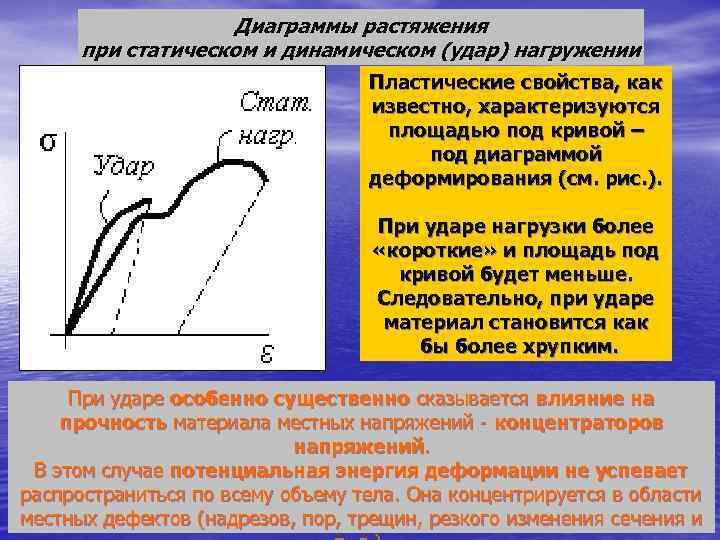Диаграммы растяжения при статическом и динамическом (удар) нагружении Пластические свойства, как известно, характеризуются площадью под кривой – под диаграммой деформирования (см. рис. ). При ударе нагрузки более «короткие» и площадь под кривой будет меньше. Следовательно, при ударе материал становится как бы более хрупким. При ударе особенно существенно сказывается влияние на прочность материала местных напряжений - концентраторов напряжений. В этом случае потенциальная энергия деформации не успевает распространиться по всему объему тела. Она концентрируется в области местных дефектов (надрезов, пор, трещин, резкого изменения сечения и

16. 3. 1. Ударная вязкость В связи с особенностями поведения материала при ударном нагружении, необходимо наряду с механическими испытаниями проводить испытания на удар, в частности, испытания материалов на ударную вязкость. Ударная вязкость – механическая характеристика материала, она определяется отношением работы внешних сил [Дж], затраченной на разрушение образца к площади поперечного сечения [м 2] в месте надреза и характеризует способность материала сопротивляться хрупкому разрушению (его трещиностойкость). Испытания на ударную вязкость актуальны для сварных соединений, для конструкций, работающих при низких температурах. С понижением температуры ударная вязкость материалов снижается. Даже пластичные материалы будут разрушаться хрупко.

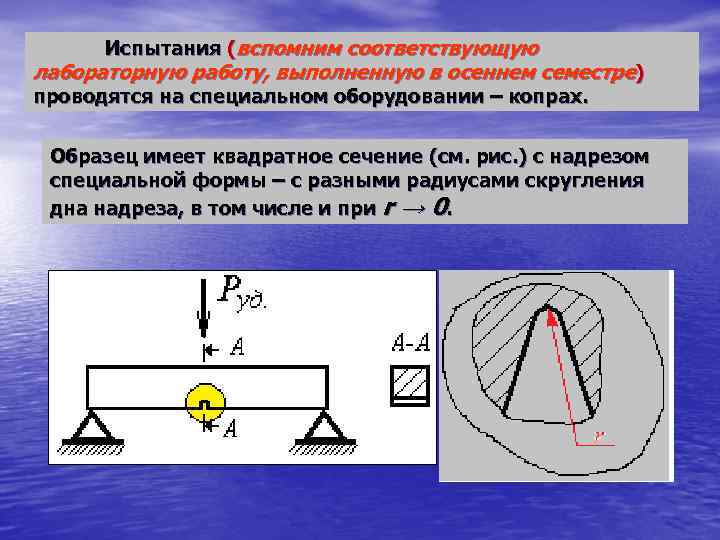Испытания (вспомним соответствующую лабораторную работу, выполненную в осеннем семестре) проводятся на специальном оборудовании – копрах. Образец имеет квадратное сечение (см. рис. ) с надрезом специальной формы – с разными радиусами скругления дна надреза, в том числе и при r → 0.

16. 3. 2. Приближенная теория удара Решение инженерных задач расчета при ударе обычно строится на основе приближенной теории удара. При этом принимаются следующие допущения: 1). Кинетическая энергия ударяющего тела полностью переходит в потенциальную энергию деформации ударяемого тела; при этом пренебрегают энергией, идущей на деформацию ударяющего тела и основания, на котором находится ударяемое тело. Это допущение идет в запас прочности, так как ставит ударяемое тело в худшие условия, чем это имеет место в действительности. То есть удар рассматривается как абсолютно неупругий;

2) Закон распределения напряжений и деформаций по объему ударяемого тела остается таким же, как и при статическом действии сил; при этом не учитывается изменение распределения напряжений и деформаций в том месте, где происходит соударение тел, а также влияние колебаний высокой частоты, сопровождающих явление удара во всем объеме тела. Иначе говоря, материал ударяемой детали подчиняется закону Гука в определенном интервале ударных нагрузок. Этот вывод подтверждается опытами. Рассмотрим методику расчета на прочность при ударе без учета массы упругой системы. Всем параметрам, определяемым при ударе, будем присваивать индекс «д» .

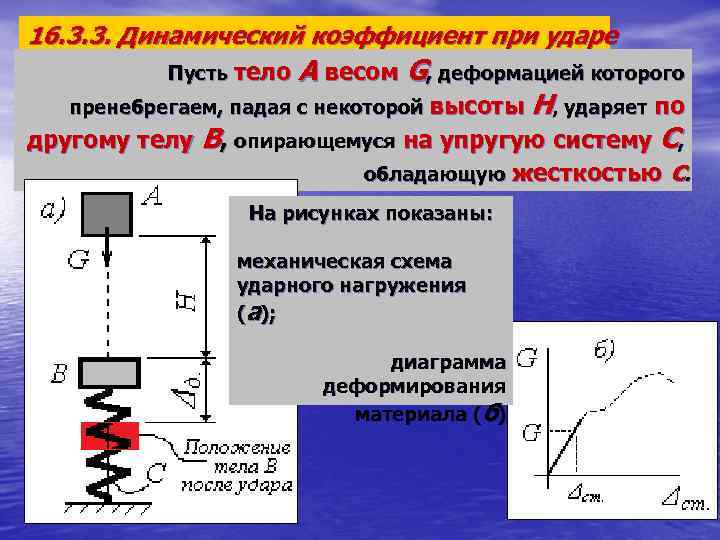16. 3. 3. Динамический коэффициент при ударе А весом G, деформацией которого пренебрегаем, падая с некоторой высоты H, ударяет по другому телу В, опирающемуся на упругую систему С, обладающую жесткостью с. Пусть тело На рисунках показаны: механическая схема ударного нагружения (а); диаграмма деформирования материала (б)

В течении очень короткого времени упругая система С испытает некоторую деформацию. Обозначим через Δд. перемещение тела В (местной деформацией его пренебрегаем) в направлении удара. В результате удара в упругой системе С возникнут напряжения: нормальные или касательные. Вид напряжений зависит от вида нагружения ударяемого тела. В соответствии с первым допущением (кинетическая энергия Т ударяющего тела полностью переходит в потенциальную энергию Uд. деформации упругой системы) запишем равенство:

К моменту завершения деформации упругой системы С ударяющее тело А пройдет путь Следовательно его запас энергии будет измеряться произведенной им работой: Вычислим потенциальную энергию при ударе Uд. . Воспользуемся вторым допущением (о законах распределения напряжений при статическом и динамическом нагружении). При статической деформации в пределах действия закона Гука потенциальная энергия деформации определяется, как известно, площадью под кривой – в данном случае площадью треугольника на участке пропорциональности: (16. 24) (16. 23)

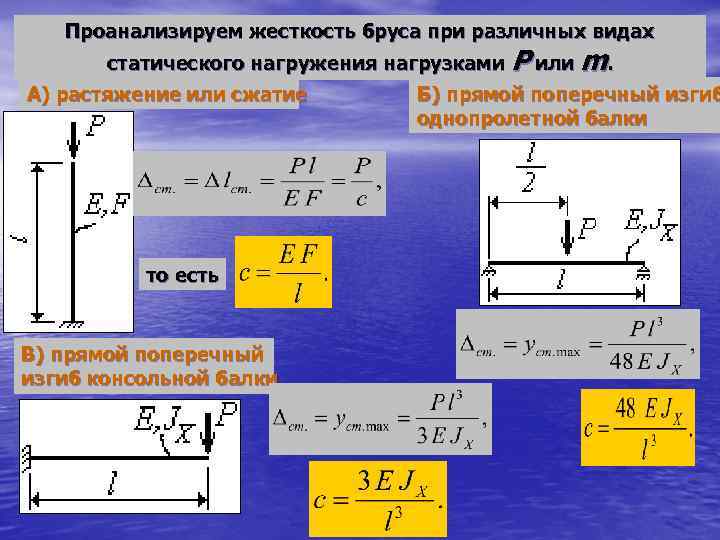Проанализируем жесткость бруса при различных видах статического нагружения нагрузками Р или m. А) растяжение или сжатие Б) прямой поперечный изгиб однопролетной балки то есть В) прямой поперечный изгиб консольной балки

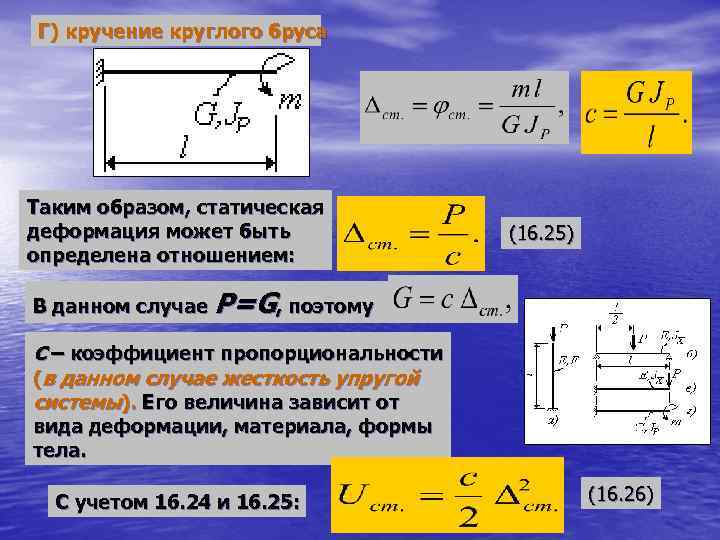Г) кручение круглого бруса Таким образом, статическая деформация может быть определена отношением: (16. 25) В данном случае P=G, поэтому с – коэффициент пропорциональности (в данном случае жесткость упругой системы). Его величина зависит от вида деформации, материала, формы тела. С учетом 16. 24 и 16. 25: (16. 26)

С учетом аналогии со статическим приложением нагрузки рассмотрим ее ударное приложение (в соответствии со вторым допущением). Упругая система С под действием упавшего груза G деформируется, иначе говоря, сила вызовет перемещение Δд. . Следуя зависимостям (16. 24 – 16. 26) можно записать: Подставим полученные значения Т (из 13. 23) и Uд. (из 16. 27) в равенство энергий: Сократим левую и правую части на G и проведем преобразования этого равенства. (16. 27)

Наибольшее значение величина деформации будет иметь при знаке (+) перед корнем, следовательно: (16. 28) Преобразуем подкоренное выражение: Тогда (16. 28) примет вид: (16. 29) ДИНАМИЧЕСКИЙ КОЭФФИЦИЕНТ ПРИ УДАРЕ: (16. 30)

В полученной формуле Δст. есть ПЕРЕМЕЩЕНИЕ сечения бруса, в котором СТАТИЧЕСКИ приложена внешняя нагрузка. В случае, если внешняя нагрузка приложена внезапно (мгновенно), высота падения груза может быть принята равной нулю: H=0. Из формулы (13. 30) получим КД = 2. При мгновенном приложении нагрузки ДИНАМИЧЕСКИЙ КОЭФФИЦИЕНТ равен 2.

По закону Гука напряжения и усилия пропорциональны деформации, поэтому По аналогии со статическим приложением нагрузки, запишем УСЛОВИЕ ПРОЧНОСТИ ПРИ УДАРЕ: (16. 32) основная задача при проведении расчетов на удар – определение Таким образом,

Используя некоторые известные из курсов физики и механики соотношения, получим другие формулы для расчета динамического коэффициента: 1. Если может быть определена скорость v ударяющего тела в момент удара (при соударении), то Тогда Получаем: 2. В соответствии с (16. 23) и (16. 24) определим: кинетическая энергия в момент, предшествующий удару потенциальная энергия при статическом приложении нагрузки Преобразуем подкоренное выражение из (16. 30), помножив числитель и знаменатель на G: (16. 33)

получаем: (16. 34) Выше было показано (см. слайды № 10 № 11: рисунок и примеры А, Б, В, Г зависит от вида нагружения. Поэтому динамический коэффициент определяется по (16. 34), с учетом вида ударного нагружения: продольный растягивающий (сжимающий) удар; изгибающий удар посередине балки; изгибающий удар по консоли; скручивающий удар и т. п.

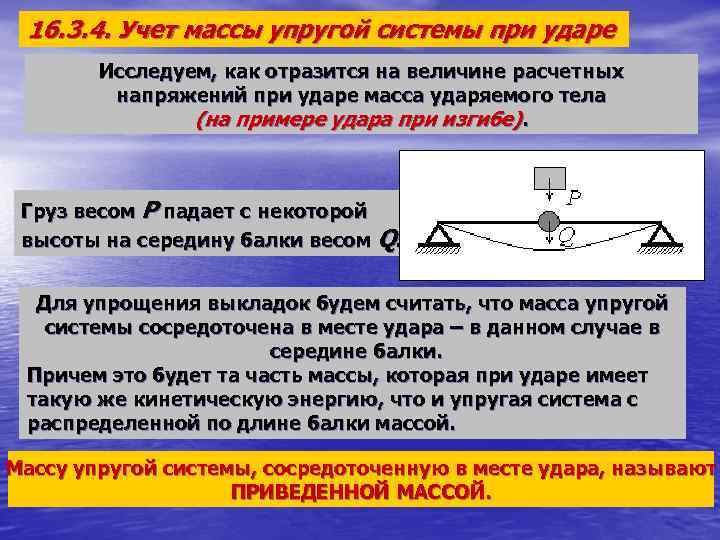16. 3. 4. Учет массы упругой системы при ударе Исследуем, как отразится на величине расчетных напряжений при ударе масса ударяемого тела (на примере удара при изгибе). Груз весом Р падает с некоторой высоты на середину балки весом Q. Для упрощения выкладок будем считать, что масса упругой системы сосредоточена в месте удара – в данном случае в середине балки. Причем это будет та часть массы, которая при ударе имеет такую же кинетическую энергию, что и упругая система с распределенной по длине балки массой. Массу упругой системы, сосредоточенную в месте удара, называют ПРИВЕДЕННОЙ МАССОЙ.

Масса падающего тела будет равна масса упругой системы – Приведенная масса – коэффициент приведения. Для примера: при продольном растягивающем или сжимающем ударе при изгибающем ударе Посередине однопролетной балки Для определения необходимо найти кинетическую энергию упругой системы в момент удара с учетом ее массы.

Вначале следует найти скорость упругой системы и скорость падающего груза после удара. Известно, что количество движения есть величина постоянная: количество движения до удара равно количеству движения после удара. Количество движения системы до удара равно Здесь v 0 есть скорость только падающего тела, т. к. до удара упругая система находится в покое (скорость ее равна нулю). Количество движения системы после удара равно v – скорость системы после удара.

Получаем: откуда Определим кинетическую энергию системы, зная, что: T=PH; v 2=2 g. H. Считая удар неупругим, получим: Если кинетическую энергию падающего тела обозначить то кинетическая энергия системы Следовательно, с учетом (16. 34) динамический коэффициент: (16. 35)

Аналогично, если учесть массу упругой системы для (16. 30), получим: (16. 36) Таким образом, при учете массы упругой системы напряжения и деформации становятся меньше на 16. 3. 5. Примеры № 1. На двутавровую балку № 16 с высоты H =4 см падает груз G=2 к. Н. Определить максимальные напряжения.

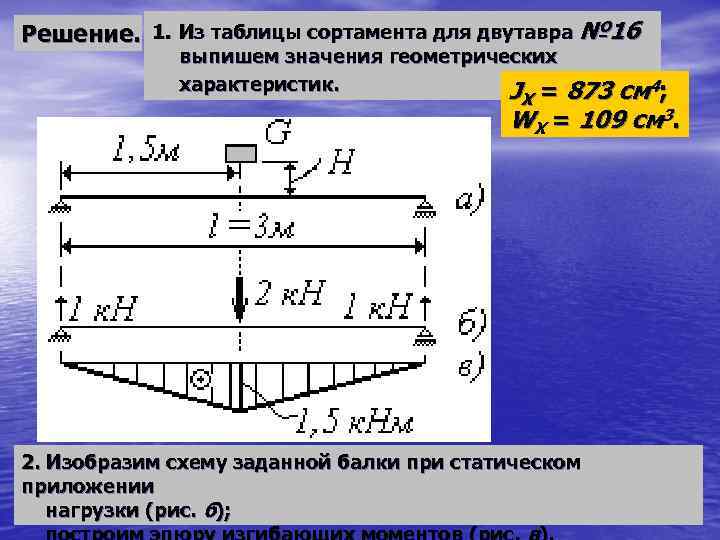Решение. 1. Из таблицы сортамента для двутавра № 16 выпишем значения геометрических характеристик. J = 873 см 4; X WX = 109 cм 3. 2. Изобразим схему заданной балки при статическом приложении нагрузки (рис. б);

и определим максимальные нормальные напряжения при статическом приложении силы: 3. Определим статическое перемещение сечения балки в месте удара (прогиб посередине пролета), для чего используем метод Верещагина. Для единичной схемы (рис. г) построим эпюру изгибающих моментов (рис. д). Перемножим эпюры д) и в):

4. Определим динамический коэффициент: 5. Максимальное напряжение при ударе: Напряжения при ударе превышают их допускаемое значение для стали, следовательно, прочность балки не будет обеспечена. При статическом же приложении нагрузки величина напряжений невелика и запас прочности достаточно большой.

№ 2. На стальную стойку, длина которой с высоты падает тело весом Площадь поперечного сечения стойки Модуль упругости I рода Определить максимальные напряжения. Решение. 1. В соответствии с теорией удара 2. При статическом приложении внешней нагрузки G имеем осевое сжатие. Тогда статические нормальные напряжения в любом сечении по высоте стойки будут максимальными и равными

3. Определим динамический коэффициент, для чего подсчитаем статическое перемещение сечения, где приложен вес G. При центральном сжатии, в соответствии с формулой закона Гука: Тогда Максимальные напряжения при ударе:

№ 3. На стальном канате подъемника подвешен груз P=20 к. Н. Груз опускается с помощью лебедки. Скорость опускания груза Площадь поперечного сечения каната Длина каната от лебедки до груза Модуль упругости материала Определить наибольшие напряжения в материале каната при внезапной остановке барабана лебедки.

Решение. При статическом приложении нагрузки имеем осевое растяжение: Динамический коэффициент: Наибольшие нормальные напряжения

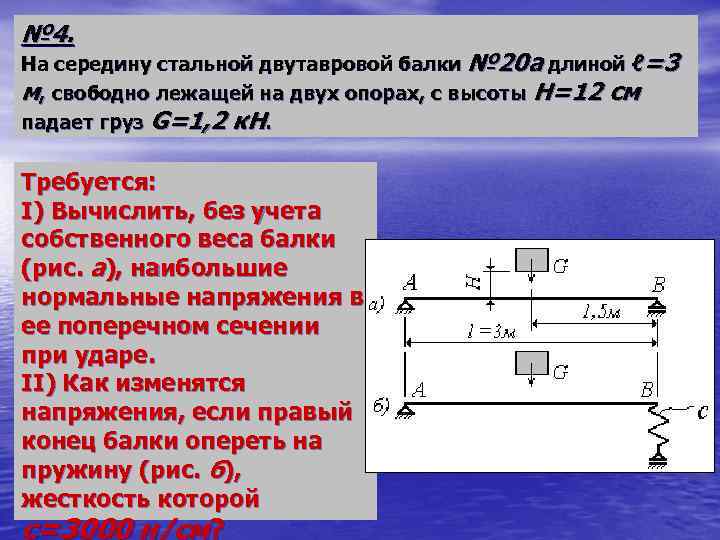№ 4. На середину стальной двутавровой балки № 20 а длиной ℓ=3 м, свободно лежащей на двух опорах, с высоты H=12 см падает груз G=1, 2 к. Н. Требуется: I) Вычислить, без учета собственного веса балки (рис. а), наибольшие нормальные напряжения в ее поперечном сечении при ударе. II) Как изменятся напряжения, если правый конец балки опереть на пружину (рис. б), жесткость которой с=3000 н/см?

Зададимся дополнительными данными. из таблицы сортамента для двутавра № 16 а: Модуль упругости материала Решение. 1). Рассмотрим решение задачи для варианта (рис. а При статическом ). приложении нагрузки G посередине балки (рис. в): прямой поперечный изгиб. Максимальные нормальные напряжения: Максимальный изгибающий момент в середине пролета:

Определим величину максимальных нормальных напряжений при статическом приложении нагрузки: Статическое перемещение точки приложения нагрузки Δст. I = yст. max есть прогиб посередине пролета. Его можно определить одним из известных методов (начальных параметров, интеграл Мора, метод Верещагина), или по формуле: Определяем значение динамического коэффициента:

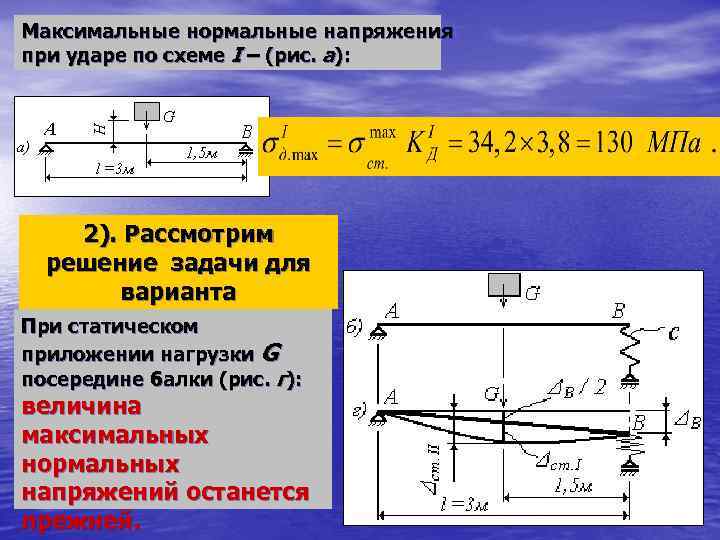Максимальные нормальные напряжения при ударе по схеме I – (рис. а): 2). Рассмотрим решение задачи для варианта (рис. б При статическом). приложении нагрузки G посередине балки (рис. г): величина максимальных нормальных напряжений останется прежней.

Статическое перемещение точки приложения нагрузки будет складываться из двух значений: – перемещения середины пролета в связи с деформацией пружины на опоре В (балка остается прямой – не деформируется): ΔВ /2; – прогиба посередине пролета: Δст. I = yст. max. Его значение нами уже определено. Под действием нагрузки пружина на опоре В деформируется (укорачивается).

Нагрузка на опоре равна реакции на этой опоре: укорочение пружины под действием реакции опоры: Статическое перемещение для варианта II:

Значение динамического коэффициента: Максимальные нормальные напряжения при ударе по схеме II – (рис. б): Для второй схемы балки напряжения уменьшились в 2, 43 раза (почти на 61%).