16 10 13 Лекция 5 Предикатное программирование 4

16. 10. 13 Лекция 5 Предикатное программирование 4. Система правил доказательства корректности программы Правила для общего случая Правила для вхождений операторов под квантором существования и в левой части Правила для однозначной спецификации Задачи верификации и синтеза 5. Построение языка предикатного программирования. Методы док-ва корректности предикатных программ Язык P 1: подстановка определения предиката на место вызова Язык P 2: оператор суперпозиции и параллельный оператор общего вида Язык P 2: другое обобщение оператора суперпозиции Язык P 3: выражения 3. Математические основы 3. 3. Матиндукция

[P(x), Q(x, y)] спецификация программы S(x: y), P(x) предусловие, Q(x, y) постусловие. Тотальная корректность программы S(x: y) относительно спецификации [P(x), Q(x, y)] : Corr(S, P, Q) (x) P(x) [ L(S(x: y)) Q(x, y) ] & y. L(S(x: y)) (6) Однозначность программы, тотальность и однозначность спецификации : SP(P, S) y 1, y 2. P(x) & L(S(x: y 1)) & L(S(x: y 2)) y 1 = y 2 (7) T(P, Q)(x) P(x) y. Q(x, y) (8) SV(P, Q)(x) y 1, y 2. P(x) & Q(x, y 1) & Q(x, y 2) y 1 = y 2 (9)

Теорема 2. 1 тождества спецификации и программы P(x) { S (x, y) } Q(x, y) (2. 1) Оператор S(x, y) является однозначным, а спецификация [P(x), Q(x, y)] тотальной. Пусть истина формула: P(x) & Q(x, y) L(x, y) (2. 6) Тогда программа (2. 1) является корректной. SP(P, S); T(P, Q)(x); x, y. P(x) & Q(x, y) L(S(x: y)) T 1: T 0: Corr(S, P, Q)(x) y. P(x) & L(S(x: y)) Q(x, y); P(x) y. L(S(x: y)) Corr(S, P, Q)(x) посылки T 1. 2 и T 1. 3

Система правил декомпозиции доказательства корректности программы. Общий случай Параллельный оператор QP: Corr(B, P, QB)(x); Corr(C, P, QC)(x); Corr(B(x: y) C(x: z), P, x, y, z. QB(x, y) & QC(x, z))(x) Доказательство истинности правила QP. Допустим, истинно предусловие P(x). Необходимо доказать тотальность формулы L(A(x: y) || B(x: z)) и выводимость из этой формулы постусловия Q(x, y) & R(x, z). Формула L(B(x: y) || C(x: z)) эквивалентна L(B(x: y) & L(C(x: z)). Из истинности P(x) и корректности операторов B(x: y) и С(x: z) следует истинность следующих формул: L(B(x: y)) Q(x, y), y. L(B(x: y)), L(C(x: z)) R(x, z) и z. L(C(x: z)). Конъюнкция y. L(B(x: y)) и z. L(C(x: z)) дает тотальность формулы L(A(x: y) || B(x: z)). Выводимость Q(x, y) & R(x, z) также очевидна. □

Условный оператор Corr(B, x. P(x) & E(x), Q)(x); Corr(C, x. P(x) & E(x), Q)(x); QC: Corr( if (E(x)) B(x: y) else C(x: y), P, Q)(x) Доказательство QC. Пусть истинно P(x). Необходимо доказать тотальность L(if (E) B(x: y) else C(x: y)) и выводимость из нее постусловия Q(x, y). Формула L(if (E) B(x: y) else C(x: y)) эквивалентна: (E L(B(x: y))) ( E L(C(x: y))). Пусть E истинно. Из истинности P(x) & E и корректности B(x: y) следует y. L(B(x: y)). Далее, будет истинной формула y. (E L(B(x: y))). Из истинности E следует истинность E L(C(x: y)) и, значит, формулы y. [(E L(B(x: y))) & ( E L(C(x: y)))]. Это доказывает тотальность L(if (E) B(x: y) else C(x: y)) для истинного E. Тотальность в случае ложного E доказывается аналогичным образом.

Оператор суперпозиции QS: P(x) z. L(B(x: z)); z. Corr(C, x, z. P(x) & L(B(x: z)), Q) (z); Corr(B(x: z); C(z: y), P, Q)(x) Доказательство QS. Необходимо доказать тотальность L(B(x: z); C(z: y)) и выводимость постусловия Q(x, y) из L(B(x: z); C(z: y)). Формула L(B(x: z); C(z: y)) эквивалентна z. L(B(x: z)) & L(C(z: y)). Из истинности предусловия P(x) и QS. 1 следует z. L(B(x: z)). Допустим, для некоторого z 0 формула L(B(x: z 0)) истинна. Из QS. 2 следует истинность L(C(z 0: y)) Q(x, y) и y. L(C(z 0: y)). Тогда y. z. L(B(x: z)) & L(C(z: y)) ( тотальность L(B(x: z); C(z: y)) ). Пусть L(B(x: z); C(z: y)) истинно, т. е. z. L(B(x: z)) & L(C(z: y)). Пусть формула истинна при z 1. Подставляя z 1 в QS. 2 получим истинность Q(x, y). □

Декомпозиция вхождений операторов Оператор суперпозиции ES: R(x) ├ z. L(B(x: z)); R(x) & L(B(x: z))├ y. L(C(z: y)) R(x) ├ y. L(B(x: z); C(z: y)) Доказательство ES. Формула y. L(B(x: z); C(z: y)) эквивалентна y. z. (L(B(x: z)) L(C(z: y))). Пусть истинно R(x). Из ES. 1 истинна z. L(B(x: z)). Допустим, для z 0 истинна L(B(x: z 0)). Из ES. 2 истинна формула y. L(C(z 0: y)). В итоге будет истинна y. z. (L(B(x: z)) L(C(z: y))). □ R(x) & L(B(x: z)) & L(C(z: y)) H(x, y) FLS: R(x) & L(B(x: z); C(z: y)) H(x, y) Доказательство FLS. Пусть истинно R(x) & L(B(x: z); C(z: y)). Формупа L(B(x: z); C(z: y)) эквивалентна z. L(B(x: z)) L(C(z: y)). Допустим, формула истинна при z 0. Тогда истинны L(B(x: z 0)) и L(C(z 0: y)). Применение FLS. 1 доказывает истинность H(x, y).

4. Система правил доказательства корректности операторов (прод 1)

Правила для корректных подоператоров Правило для параллельного оператора Corr(B, PB, QB)(x); Corr(C, PC, QC)(x); P(x) PB(x) & PC(x); y, z. QB(x, y) & QC(x, z) Q(x, y, z) RP: Corr(B(x: y) || C(x: z), P, Q) (x) Доказательство RP. Пусть P(x) истинно. Следует доказать тотальность L(B(x: y) || C(x: z)) и выводимость постусловия Q(x, y, z) из L(B(x: y) || C(x: z)). Формула L(B(x: y) || C(x: z)) эквивалентна L(B(x: y)) & L(C(x: z)). Из истинности P(x) и RP. 3 следует истинность PB(x) и PC(x). Далее, из корректности операторов B(x: y) и C(x: z) следует истинность формул y. L(B(x: y)) и z. L(C(x: z)). Их конъюнкция определяет тотальность L(B(x: y) || C(x: z)).

Правило для параллельного оператора Corr(B, PB, QB)(x); Corr(C, PC, QC)(x); P(x) PB(x) & PC(x); y, z. QB(x, y) & QC(x, z) Q(x, y, z) RP: Corr(B(x: y) || C(x: z), P, Q) (x) Доказательство RP (прод). Докажем выводимость Q(x, y, z) из L(B(x: y)) & L(C(x: z)). Допустим, истинна формула L(B(x: y)) & L(C(x: z)). Из истинности PB(x) и PC(x) и корректности операторов B(x: y) и C(x: z) следует истинность формул L(B(x: y)) QB(x, y) и L(C(x: z)) QC(x, z). Как следствие, будут истинны QB(x, y) и QC(x, z). Наконец, из RP. 4 следует истинность постусловия Q(x, y, z). □

Правило для оператора суперпозиции RS: Corr*(B, PB, QB)(x); z Corr*(C, PC, QC)(z); P(x) P*B(x); z. P(x) & QB(x, z) P*C(z); z, y. P(x) & QB(x, z) & QC(z, y) Q(x, y) Corr(B(x: z); C(z: y), P, Q)(x) Доказательство RS. Пусть P(x) истинно. Следует доказать тотальность L(B(x: z); C(z: y)) и выводимость постусловия Q(x, y) из L(B(x: z); C(z: y)). Формула L(B(x: z); C(z: y)) эквивалентна z. L(B(x: z)) & L(C(z: y)). Из истинности предусловия P(x) и RS. 3 следует PB(x). Далее, из RS. 4 следует QB(x, z) PC(z). Из истинности PB(x) и корректности оператора B(x: z) следует истинность формул z. L(B(x: z)) и L(B(x: z)) QB(x, z). Допустим, для некоторого z 0 формула L(B(x: z 0)) истинна. Как следствие, истинно QB(x, z 0).

Правило для оператора суперпозиции RS: Corr*(B, PB, QB)(x); z Corr*(C, PC, QC)(z); P(x) P*B(x); z. P(x) & QB(x, z) P*C(z); z, y. P(x) & QB(x, z) & QC(z, y) Q(x, y) Corr(B(x: z); C(z: y), P, Q)(x) Доказательство RS (прод 1). Далее, из истинности z (QB(x, z) PC(z)) следует истинность PC(z 0). Ввиду корректности оператора C(z: y) истинна формула y L(C(z 0: y)). Далее, истинна L(B(x: z 0)) & y L(C(z 0: y)), и затем – формула y. z. L(B(x: z)) & L(C(z: y)), т. е. доказана тотальность L(B(x: z); C(z: y)).

Правило для оператора суперпозиции RS: Corr*(B, PB, QB)(x); z Corr*(C, PC, QC)(z); P(x) P*B(x); z. P(x) & QB(x, z) P*C(z); z, y. P(x) & QB(x, z) & QC(z, y) Q(x, y) Corr(B(x: z); C(z: y), P, Q)(x) Доказательство RS (прод 2). Докажем выводимость Q(x, y) из L(B(x: z); C(z: y)). Пусть L(B(x: z); C(z: y)) истинно, т. е. истинна формула z. L(B(x: z)) & L(C(z: y)). Пусть формула истинна для некоторого z 1. Ввиду корректности оператора B(x: z) истинна формула L(B(x: z 1)) QB(x, z 1) и далее – QB(x, z 1). Истинность QB(x, z 1) и z (QB(x, z) PC(z)) влечет PC(z 1). Из корректности оператора C(z: y) истинно L(C(z 1, y)) QC(z 1, y). Поскольку L(C(z 1, y)) истинно, то истинно QC(z 1, y). В итоге, истинна правая часть RS. 5, а значит – и левая, т. е. истинно постусловие Q(x, y). □

Декомпозиция в случае однозначной спецификации Правило для параллельного оператора R(x, y, z) ├ L(B(x: y)); R(x, y, z) ├ L(C(x: z)) FP: R(x, y, z) ├ L(B(x: y) || C(x: z)) Правило для оператора суперпозиции R(x, y) ├ z. L(B(x: z)); R(x, y) & L(B(x: z))├ L(C(z: y)) FS: R(x, y) ├ L(B(x: z); C(z: y))

Задачи верификации и синтеза на примере оператора суперпозиции A(x: y) pre P(x) { B(x: z); C(z: y) } post Q(x, y) (3) RS: Corr*(B, PB, QB)(x); z Corr*(C, PC, QC)(z); P(x) P*B(x); z. P(x) & QB(x, z) P*C(z); z, y. P(x) & QB(x, z) & QC(z, y) Q(x, y) Corr(B(x: z); C(z: y), P, Q)(x) Задача дедуктивной верификации Задача программного синтеза: требуется построить программу предиката A, представленного спецификацией [P(x), Q(x, y)]. Пусть для некоторых предикатов PB(x), QB(x, z), PC(z) и QC(z, y) доказана истинность посылок RS. 3, RS. 4 и RS. 5. Тогда синтезируем программу (3). Дальнейшей целью является синтез программ предикатов B(x: z) и C(z: y).

5. Построение языка предикатного программирования. Методы доказательства корректности предикатных программ

Система правил доказательства корректности оператора суперпозиции, параллельного оператора и условного оператора Исчисление вычислимых предикатов ― язык CCP (Calculus of Computable Predicates) минимальный полный базис языка предикатного программирования для класса программ-функций Язык предикатного программирования P (Predicate programming language). Расширяющаяся последовательность языков: CCP = P 0, P 1, P 2, P 3, P 4 = P.

Язык P 1: подстановка определения предиката на место вызова Подстановка определения предиката A(x: y) K(x: y) на место вызова A(t: z) блок { K(t: z) }, где x, y, t, z наборы переменных. Происходит замена вхождений переменных и переименование локалов. L({ K(t: z) }) L(K(t: z)) (5. 1) run. Block(s, { K(t: z) }): run. Stat(s, K(t: z)) (5. 2) Программа П’, получаемая из программы П подстановкой определения предиката на место вызова, эквивалентна программе П’: исполнение любого предиката программы П’ на фиксированном наборе аргументов дает тот же результат, что и в программе П. Язык P 1: многократное произвольное применение подстановок определений предикатов на место вызовов. Конструкция: вызов или блок как подоператор в трех базисных операторах

Язык P 2: оператор суперпозиции и параллельный оператор общего вида Операторы { A(…); B(…) }; C(…) и A(…); { B(…); C(…) } являются эквивалентными Эквивалентны { A(…) || B(…) } || C(…) и A(…) || { B(…) || C(…) } Язык P 2: оператор суперпозиции и параллельный оператор общего вида: A 1(…); A 2(…); … ; An(…) и A 1(…) || A 2(…) || … || An(…) для n > 1. P(x){B 1(x: z 1); B 2(z 1: z 2); . . . ; Bj(zj-1: zj); . . . ; Bn(zn-1: y)}Q(x, y) (5. 3) x, z 1, z 2, …, zn-1, y различные непересекающиеся наборы переменных, B 1, B 2, …, Bn обозначают предикаты или блоки языка P 1 со спецификациями (предусловиями и постусловиями) PB 1(x), QB 1(x, z 1), PB 2(z 1), QB 2(z 1, z 2), …, PBn(zn-1), QBn(zn-1, y).

L(B 1(x: z 1); B 2(z 1: z 2); . . . ; Bj(zj-1: zj); . . . ; Bn(zn-1: y)) z 1, z 2, …, zn-1. L(B 1(x: z 1)) & L(B 2(z 1: z 2)) &. . . & & L(Bj(zj-1: zj)) &. . . & L(Bn(zn-1: y)) (5. 4) run. Stat(s, B 1(x: z 1); …; Bn(zn-1: y)) run. Call. Block(s, B 1(x: z 1)); run. Call. Block(s, B 2(z 1: z 2)); . . . ; run. Call. Block(s, Bj(zj-1: zj)); . . . ; run. Call. Block(s, Bn(zn-1: y)) (5. 5)

Параллельный оператор общего вида P(x){B 1(x: y 1) || B 2(x: y 2)||. . . ||Bj(x: yj)||. . . ||Bn(x: yn)}Q(x, y) (5. 7) x, y = y 1, …, yn различные непересекающиеся наборы переменных, B 1, B 2, …, Bn предикаты или блоки языка P 1 со спецификациями PB 1(x), QB 1(x, y 1), PB 2(x), QB 2(x, y 2), …, PBn(x), QBn(x, yn). L(B 1(x: y 1) || B 2(x: y 2) ||. . . || Bj(x: yj) ||. . . || Bn(x: yn)) L(B 1(x: y 1)) & L(B 2(x: y 2)) &. . . & & L(Bj(x: yj)) &. . . & L(Bn(x: yn)) (5. 8) run. Stat(s, B 1(…) || B 2(…) || … || Bn(…)) run. Call. Block(s, B 1(x: y 1)) || run. Call. Block(s, B 2(x: y 2)) ||. . . || run. Call. Block(s, Bj(x: yj)) ||. . . || run. Call. Block(s, Bn(x: yn)) (5. 9)

Правило опускания скобок: {A(…); B(…)} || C(…) A(…); B(…) || C(…). A(x: y); {B(z: t) || C(u: v)} Набор y пересекается с набором z и не пересекается с набором u. Тогда A(x: y); {B(z: t) || C(u: v)} {A(x: y); B(z: t)} || C(u: v) A(x: y); B(z: t) || C(u: v). {A(x: y) || B(z: t)}; C(u: v) A(x: y) || B(z: t); C(u: v), если наборы y и u не пересекаются.

Язык P 2: другое обобщение оператора суперпозиции B(x: z); C(x, z: y) обобщение оператора суперпозиции. P(x) {B 1(x: z 1); B 2(x, z 1: z 2); . . . ; Bj(x, zj-1: zj); . . . ; Bn(x, zn-1: y)} Q(x, y) (5. 10) Частный случай: B(x: z); C(u, z: y), набор u часть набора x Наиболее общая форма суперпозиции: A(x: t, y) P(x) {B(x: z, t); C(x, z: y)} Q(x, t, y) (5. 11) наборы x и t могут быть пустыми Спецификации: PB(x), QB(x, z, t), PC(x, z), QC(x, z, y).

A(x: t, y) P(x) {B(x: z, t); C(x, z: y)} Q(x, t, y) (5. 11) B 1(x: x 1, z, t 1) PB(x) {B(x: z, t 1) || x 1 = x} QB(x, z, t 1) & x 1 = x C 1(x 1, z, t 1: y, t) PC(x 1, z) {C(x 1, z: y) || t = t 1} QC(x 1, z, y) & t = t 1 Поскольку B 1(x: x 1, z, t 1); C 1(x 1, z, t 1: t, y) B(x: z, t); C(x, z: y), то справедливо другое определение предиката A: A(x: t, y) P(x) {B 1(x: x 1, z, t 1); C 1(x 1, z, t 1: t, y)} Q(x, t, y) (5. 12) Логическая семантика: L(B(x: z, t); C(x, z: y)) z. (L(B(x: z, t)) & L(C(x, z: y))) (5. 13) Операционная семантика: run. Call. Block(s, B(x: z, t)); run. Call. Block (s, C(x, z: y)) (5. 14)

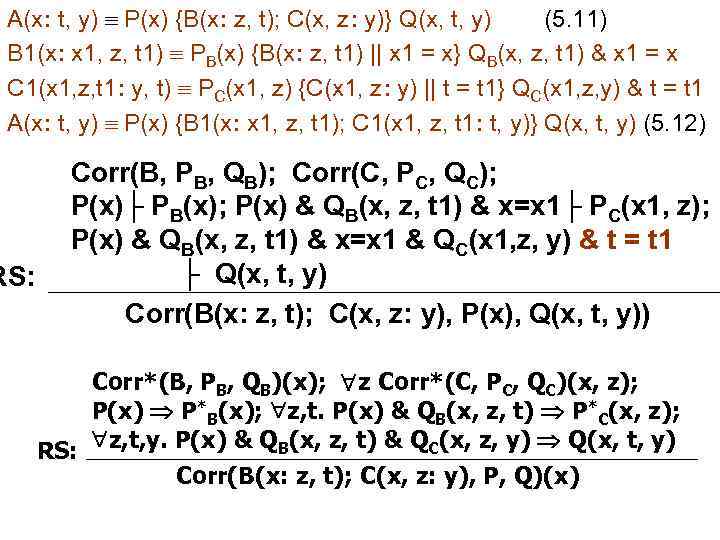A(x: t, y) P(x) {B(x: z, t); C(x, z: y)} Q(x, t, y) (5. 11) B 1(x: x 1, z, t 1) PB(x) {B(x: z, t 1) || x 1 = x} QB(x, z, t 1) & x 1 = x C 1(x 1, z, t 1: y, t) PC(x 1, z) {C(x 1, z: y) || t = t 1} QC(x 1, z, y) & t = t 1 A(x: t, y) P(x) {B 1(x: x 1, z, t 1); C 1(x 1, z, t 1: t, y)} Q(x, t, y) (5. 12) Corr(B, PB, QB); Corr(C, PC, QC); P(x)├ PB(x); P(x) & QB(x, z, t 1) & x=x 1├ PC(x 1, z); P(x) & QB(x, z, t 1) & x=x 1 & QC(x 1, z, y) & t = t 1 RS: ├ Q(x, t, y) Corr(B(x: z, t); C(x, z: y), P(x), Q(x, t, y)) Corr*(B, PB, QB)(x); z Corr*(C, PC, QC)(x, z); P(x) P*B(x); z, t. P(x) & QB(x, z, t) P*C(x, z); RS: z, t, y. P(x) & QB(x, z, t) & QC(x, z, y) Q(x, t, y) Corr(B(x: z, t); C(x, z: y), P, Q)(x)

A(x: t, y) P(x) {B(x: z, t); C(x, z: y)} Q(x, t, y) (5. 11) B 1(x: x 1, z, t 1) PB(x) {B(x: z, t 1) || x 1 = x} QB(x, z, t 1) & x 1 = x C 1(x 1, z, t 1: y, t) PC(x 1, z) {C(x 1, z: y) || t = t 1} QC(x 1, z, y) & t = t 1 A(x: t, y) P(x) {B 1(x: x 1, z, t 1); C 1(x 1, z, t 1: t, y)} Q(x, t, y) (5. 12) Случай однозначной спецификации: FS: R(x, y) ├ z. L(B(x: z)); R(x, y) & L(B(x: z))├ L(C(x, z: y)) R(x, y) ├ L(B(x: z); C(x, z: y)) R(x, t, y) ├ z, t. L(B(x: z, t)) R(x, t, y) & L(B(x: z, t 1)) ├ L(C(x, z: y)) & t = t 1 FSQ: R(x, t, y) ├ L(B(x: z, t); C(x, z: y))

Язык P 3: выражения Функциональная форма. Предикат A(t: z). z = A(t) A(t: z) |z| = A(t), если z набор Инфиксная и постфиксная нотация как разновидность функциональной формы +(x, y: z), -(x: y), <(x, y: b) z = x + y, z = x - y, y = -x , b = x < y. Изображения констант: Cons. Int. Zero( : x) Cons. Int. One( : x) val. Int(“ 2089” : x) x = 0 x = 1 x = 2089 B(x: z); C(x, z: y) z =B(x); C(x, z: y) C(x, B(x): y) { A(x: y) || B(z: t) }; C(y, t: u) { y = A(x) || t = B(z) }; C(y, t: u) C(A(x), B(z): u)

Понятие выражения. z = a b; y = z + c y = (a b) + c y = a b + c Правила приоритетов операций Переменные, изображения констант, вызовы функций и их представление в виде операций являются частными случаями понятия выражения. C(x: b); if (b) A(x: y) else B(x: y) else if (C(x)) A(x: y) else B(x: y) В позиции условия выражение

Правило для выражений в качестве аргументов: z Corr*(C, PC, QC)(z); SP(PB, B)(x) ; P(x) PB(x) & P*C(B(x)); y. P(x) & QC(B(x), y) Q(x, y) RB: Corr(C(B(x): y), P, Q)(x)

A 0(n: f) A 1( : c 0, c 1); A 2(n, c 0, c 1: f) A 1( : c 0, c 1) Cons. Int. Zero( : c 0) || Cons. Int. One( : c 1) A 2(n, c 0, c 1: f) =(n, c 0: b); A 3(n, c 1, b: f) if (b) =(c 1: f) else A 4(n, c 1: f) -(n, c 1: n 1); A 5(n, n 1: f) A 0(n 1: f 1); (n, f 1: f) Подставим A 1 A 0; преобразуем к функциональному виду. A 0(n: f) A 2(n, 0, 1: f) A 2(n, c 0, c 1: f) A 3(n, c 1, n = c 0: f) A 3(n, c 1, b: f) if (b) f =c 1 else A 4(n, c 1: f) A 5(n, n - c 1: f) A 5(n, n 1: f) f = n A 0(n 1) Подставим A 3 A 2, а A 2 A 0, A 5 A 4. A 0(n: f) if (n = 0) f =1 else A 4(n, 1: f) if A 4(n, c 1: f) f = n A 0(n - c 1) A 4 A 0, получим программу факториала на языке P 3. A 0(n: f) if (n = 0) f =1 else f = n A 0(n - 1)

3. Математические основы 3. 3. Математическая индукция

Математическая индукция ― метод доказательства некоторого утверждения P(n) для всех значений натурального параметра n; n = 0, 1, 2, …. Схема доказательства: Начальный шаг: утверждение P(n) доказывается для n = 0 (база индукции); Индуктивный шаг: утверждение P(n) считается истинным для значения n (индуктивное предположение) и доказывается для значения n + 1. Переменная n называется индукционной переменной. Метод математической индукции базируется на аксиоме индукции: ( P(0) & k. [ P(k) P(k + 1) ] ) n. P(n) (3. 2) Обобщения. База индукции может быть отлична от нуля. Шаг индукции может быть отрицательным. Индукционных переменных может быть несколько. Эти и другие особенности учитываются методами полной индукции и структурной индукции

Индукционное предположение для полной индукции определяет истинность P(j) для всех j k; используя его требуется доказать P(k + 1). Метод, сочетающий структурную и полную индукцию. На множестве X задан строгий частичный порядок ⊏, удовлетворяющий свойству (3. 1) обрыва бесконечных убывающих цепей (well-founded partial order) всякое непустое подмножество S имеет минимальный элемент, т. е. S X. (S a S s S. s ⊏ a). (3. 1) Пусть утверждение, которое требуется доказать, есть W(t); t X. Параметр t определяет одну или несколько индукционных переменных. t X. [ ( y X. y ⊏ t W(y) ) W(t) ] u X. W(u) (3. 3)

t X. [ ( y X. y ⊏ t W(y) ) W(t) ] u X. W(u) (3. 3) Если элемент t в формуле (3. 3) минимальный, то формула (3. 3) вырождается в t X. W(t). Это значит, что для минимальных элементов доказательство W(t) надо проводить отдельно, что соответствует начальному шагу классической схемы. Пусть истинное значение предиката (t) определяет набор значений t, составляющих базу индукции, которая, по меньшей мере, должна содержать все минимальные элементы. Тогда формула (3. 3) переписывается в виде: t X. ( (t) W(t)) & & t X. [ ( y X. (t) & y ⊏ t W(y) ) W(t) ] (3. 4) (t) ├ W(t) (t) & y ⊏ t W(y) ├ W(t)

Метод индукции, использующий меру t X. [ ( y X. m(y) < m(t) W(y) ) W(t) ] u X. W(u) (3. 5) Функция m: X nat называется мерой Вместо типа nat может использоваться ЧУМ со свойством обрыва бесконечно убывающих цепей (well-founded partial order) Induct(t, W) y. m(y) < m(t) W(y)) t X. [ Induct(t, W) W(t) ] u X. W(u) (3. 5)

Методы доказательства корректности рекурсивных программ Определения предикатов рекурсивного кольца A 1, A 2, …, An: Aj(xj: yj) Pj(xj) {Kj(xj: yj)} Qj(xj, yj); j=1…n; n > 0 (3. 36’) Здесь Pj и Qj ― предусловие и постусловие предиката Aj; xj, yj ― различающиеся наборы переменных. Aj(x: yj) Pj(x) {Kj(x: yj)} Qj(x, yj); j=1…n; n > 0 (5. 17) Набор x объединяет все наборы xj; j=1…n. Корректность определений предикатов кольца (5. 17): W(x) j=1. . n. { Pj(x) ( yj. L(Kj(x: yj))) & (L(Ki(x: yj)) Qj(x, yj))) } (5. 18) RR: Induct(t, W) W(t) W(x) RR 1: Induct(t, W)) W(t) Induct(t, W) y. m(y) < m(t) W(y)) t X. [ Induct(t, W) W(t) ] u X. W(u) (3. 5)

Рекурсивное кольцо состоит из единственного определения предиката: A(x: y) P(x) { S(x: y) } Q(x, y) (5. 20) Здесь S(x: y) оператор, в котором имеются рекурсивные вызовы предиката A. Формула корректности определения (5. 20): Corr(S(x: y), P(x), Q(x, y)) P(x) [ L(S(x: y)) Q(x, y) ] & y. L(S(x: y)) W(x) Corr(A(x: y), P(x), Q(x, y)) Corr(t, A, B(x: y), PB(x), QB(x, y)) Induct(t, A) Corr(B(x: y), PB(x), QB(x, y)) Induct(t, A) u. m(u) < m(t) Corr(A(u: y), P(u), Q(u, y)) P*(x) m(x) < m(t) & P(x) t – формальные параметры, x – фактические параметры рекурсивного вызова. R 0: Corr(x, A, S(x: y), P(x), Q(x, y)) Corr(A(x: y), P(x), Q(x, y) Induct(t, W) W(t) RR: W(x)

RS: Corr(B, PB, QB); Corr(C, PC, QC); P(x) ├ PB(x); P(x) & QB(x, z) ├ PC(z); P(x) & QB(x, z) & QC(x, z, y) ├ Q(x, y) Corr(B(x: z); C(x, z: y), P(x), Q(x, y)) Обобщение на случай рекурсии: Corr(t, A, B, PB, QB); Corr(t, A, C, PC, QC); P(x) ├ P*B(x); P(x) & QB(x, z) ├ P*C(z); P(x) & QB(x, z) & QC(x, z, y) ├ Q(x, y) RS: Corr(t, A, B(x: z); C(x, z: y), P(x), Q(x, y))

Пример 5. 1. Программа умножения через сложение. formula m(nat a: nat) = a; Умн(nat a, b: nat c) { if (a = 0) c = 0 else c = b + Умн(a – 1, b) } post c = a b measure m(a); QС: Corr(A, t, B, P & E, Q); Corr(A, t, C, P & E, Q) Corr(A, t, if (E) B(x: y) else C(x: y), P(x), Q(x, y)) Генерируются цели: formula Q(nat a, b, c) = c = a b; QC 1: Corr(Умн, a, c = 0, a = 0, Q); QC 2: Corr(Умн, a, c = b + Умн(a – 1, b), a = 0, Q) T 0: P(x) ├ y. L(S(x: y)); P(x) & L(S(x: y) ├ Q(x, y) Corr(S(x: y), P(x), Q(x, y)) Генерируется лемма применением T 0. 2: QC 1: lemma not a = 0 & c = 0 implies Q(a, b, c);