15 Math-Review Monday 8 14 00 1 General Mathematical

15. Math-Review Monday 8/14/00 1

General Mathematical Rules z Addition y Basics: y Summation Sign: y Famous Sum: 15. Math-Review 2

General Mathematical Rules z Multiplication y Basics y Squares: y Cubes: 15. Math-Review 3

General Mathematical Rules z Multiplication y General Binomial Product: y Product Sign: y Distributive Property: 15. Math-Review 4

General Mathematical Rules z Fractions y Addition: y Product: 15. Math-Review 5

General Mathematical Rules z Powers y Interpretation: y General rules: y Series: 15. Math-Review 6

General Mathematical Rules z Logarithms y Interpretation: x. The inverse of the power function. y General rules and notation: 15. Math-Review 7

General Mathematical Rules z Exercises: y We know that project X will give an expected yearly return of $20 M for the next 10 years. What is the expected PV (Present Value) of project X if we use a discount factor of 5%? y How long until an investment that has a 6% yearly return yields at least a 20% return? 15. Math-Review 8

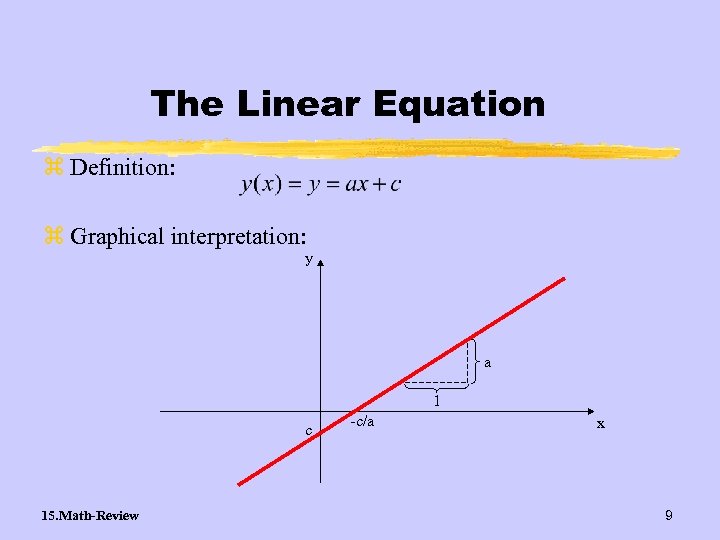The Linear Equation z Definition: z Graphical interpretation: y a 1 c 15. Math-Review -c/a x 9

The Linear Equation z Example: Assume you have $300. If each unit of stock in Disney Corporation costs $20, write an expression for the amount of money you have as a function of the number of stocks you buy. Graph this function. z Example: In 1984, 20 monkeys lived in Village Kwame. There were 10 coconut trees in the village at that time. Today, the village supports a community of 45 monkeys and 20 coconut trees. Find an expression (assume this to be linear) for, and graph the relationship between the number of monkeys and coconut trees. 15. Math-Review 10

The Linear Equation z System of linear equations 2 x – 5 y = 12 3 x + 4 y = 20 (1) (2) z Things you can do to these equalities: (a) add (1) to (2) to get: 5 x – y = 32 (b) subtract (1) from (2) to get: x + 9 y = 8 (c) multiply (1) by a factor, say, 4 8 x – 20 y = 48 z All these operations generate relations that hold if (1) and (2) hold. 15. Math-Review 11

The Linear Equation z Example: Find the pair (x, y) that satisfies the system of equations: 2 x – 5 y = 12 3 x + 4 y = 20 (1) (2) Now graph the above two equations. z Example: Solve, algebraically and graphically, 2 x + 3 y = 7 4 x + 6 y = 12 z Example: Solve, algebraically and graphically, 5 x + 2 y = 10 20 x + 8 y = 40 15. Math-Review 12

The Linear Equation z Exercise: A furniture manufacturer has exactly 260 pounds of plastic and 240 pounds of wood available each week for the production of two products: X and Y. Each unit of X produced requires 20 pounds of plastic and 15 pounds of wood. Each unit of Y requires 10 pounds of plastic and 12 pounds of wood. How many of each product should be produced each week to use exactly the available amount of plastic and wood? 15. Math-Review 13

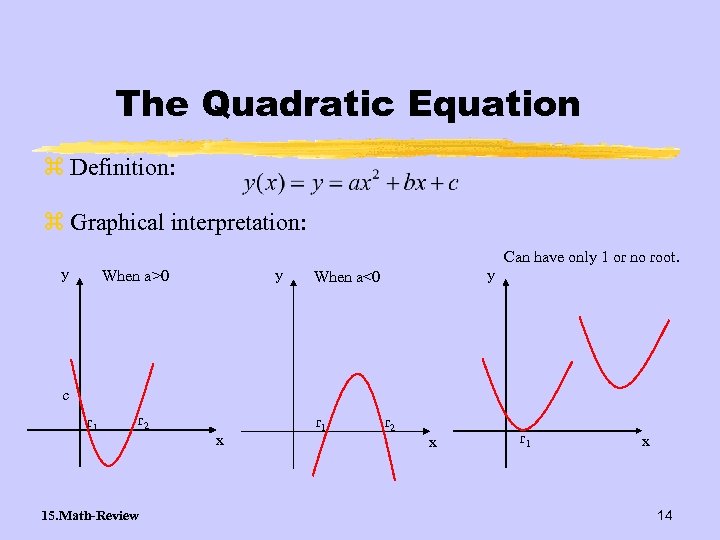The Quadratic Equation z Definition: z Graphical interpretation: y y When a>0 y When a<0 Can have only 1 or no root. c r 1 r 2 15. Math-Review x r 1 r 2 x r 1 x 14

The Quadratic Equation z Completing squares: y Another form of the quadratic equation: y The point (h, k) is at the vertex of the parabola. In this case: 15. Math-Review 15

The Quadratic Equation z Example: Find the alternate form of the following quadratic equations, by completing squares, and their extreme point. 15. Math-Review 16

The Quadratic Equation z Solving for the roots y. We want to find x such that ax 2+bx+c=0. This can be done by: x. Factoring. Finding r 1 and r 2 such that ax 2+bx+c = (x- r 1)(x- r 2) Example: x. Formula Example: 15. Math-Review 17

The Quadratic Equation z Exercise: Knob C. O. makes door knobs. The company has estimated that their revenues as a function of the quantity produced follows the following expression: z where q represents thousands of knobs, and f (q), represents thousand of dollars. y If the operative costs for the company are 20 M, what is the range in which the company has to operate? y What is the operative level that will give the best return? 15. Math-Review 18

Functions z Definition: y For 2 sets, the domain and the range, a function associates for every element of the domain exactly one element of the range. y Examples: x. Given a box of apples, if for every apple we obtain its weight we have a function. This maps the set of apples into the real numbers. x. Domain=range=all real numbers. For every x, we get f(x)=5. For every x, we get f(x)=3 x-2. For every x, we get f(x)=3 x +sin(3 x) 15. Math-Review 19

Functions z Types of functions y Linear functions y Quadratic functions y Exponential functions: f(x) = ax Example: Graph f(x) = 2 x , and f(x) = 1 -2 -x. Example: I have put my life savings of $25 into a 10 -year CD with a continuously compounded rate of 5% per year. Note that my wealth after t years is given by w = 25 e 5 t. Graph this expression to get an idea how my money grows. 15. Math-Review 20

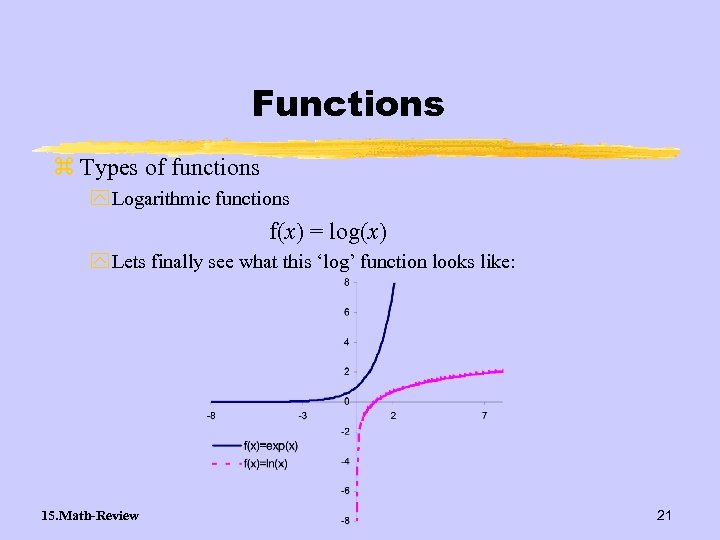Functions z Types of functions y Logarithmic functions f(x) = log(x) y Lets finally see what this ‘log’ function looks like: 15. Math-Review 21

Convexity and Concavity z Given a function f(x), a line passing through f(a) and f(b) is given by: z Definition: y f(x) is convex in the interval [a, b] if y f(x) is concave in the interval [a, b] if Another definition is f(x) is concave if -f(x) is convex 15. Math-Review 22

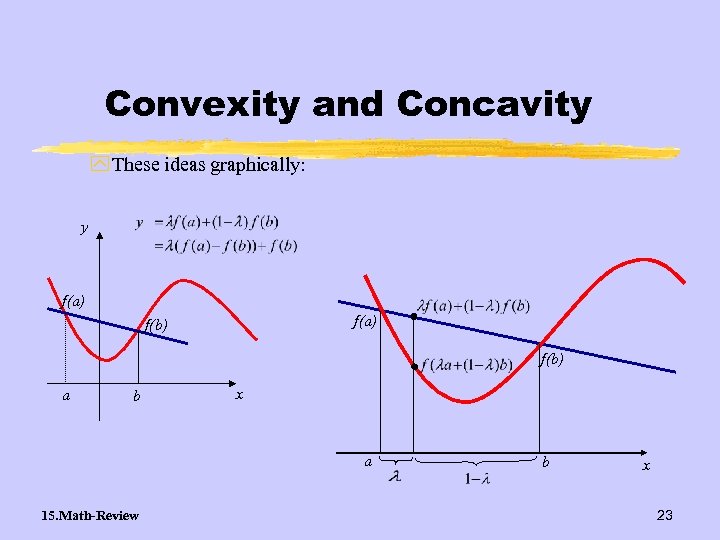Convexity and Concavity y These ideas graphically: y f(a) f(b) a b x a 15. Math-Review b x 23