Скачать презентацию 15 -745 Static Single Assignment CS 745 SSA Скачать презентацию 15 -745 Static Single Assignment CS 745 SSA

124926655eafa7d015e273de00ec024d.ppt

  • Количество слайдов: 45

15 -745 Static Single Assignment CS 745: SSA © Seth Copen Goldstein & Todd 15 -745 Static Single Assignment CS 745: SSA © Seth Copen Goldstein & Todd C. Mowry 2001 -3 1

Values Locations … for … … } for … } CS 745: SSA (i=0; Values Locations … for … … } for … } CS 745: SSA (i=0; i++; i<10) { = … i …; (i=j; i++; i<20) { = i … © Seth Copen Goldstein & Todd C. Mowry 2001 -3 2

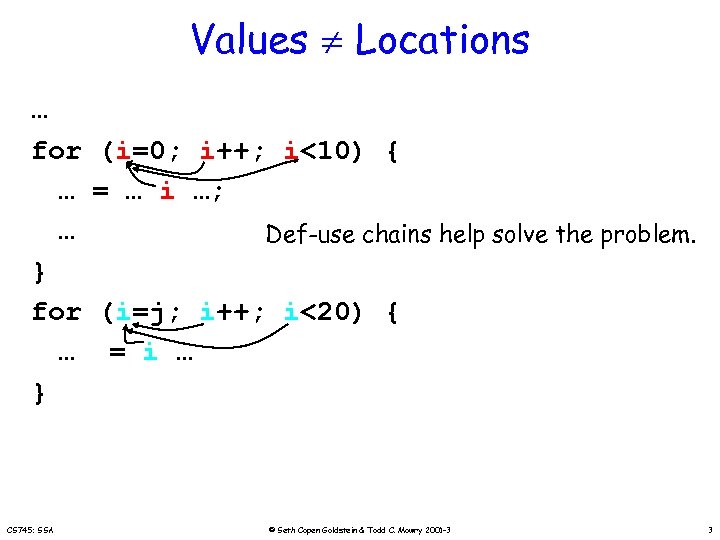Values Locations … for … … } for … } CS 745: SSA (i=0; Values Locations … for … … } for … } CS 745: SSA (i=0; i++; i<10) { = … i …; Def-use chains help solve the problem. (i=j; i++; i<20) { = i … © Seth Copen Goldstein & Todd C. Mowry 2001 -3 3

Def-Use chains are expensive foo(int i, int j) { … switch (i) { case Def-Use chains are expensive foo(int i, int j) { … switch (i) { case 0: x=3; break; case 1: x=1; break; case 2: x=6; break; case 3: x=7; break; default: x = 11; } switch (j) { case 0: y=x+7; break; case 1: y=x+4; break; case 2: y=x-2; break; case 3: y=x+1; break; default: y=x+9; } … CS 745: SSA © Seth Copen Goldstein & Todd C. Mowry 2001 -3 4

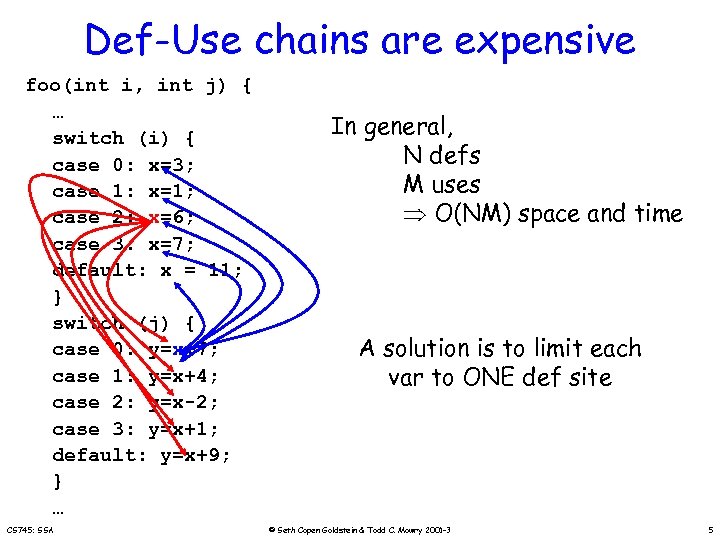Def-Use chains are expensive foo(int i, int j) { … switch (i) { case Def-Use chains are expensive foo(int i, int j) { … switch (i) { case 0: x=3; case 1: x=1; case 2: x=6; case 3: x=7; default: x = 11; } switch (j) { case 0: y=x+7; case 1: y=x+4; case 2: y=x-2; case 3: y=x+1; default: y=x+9; } … CS 745: SSA In general, N defs M uses O(NM) space and time A solution is to limit each var to ONE def site © Seth Copen Goldstein & Todd C. Mowry 2001 -3 5

Def-Use chains are expensive foo(int i, int j) { … switch (i) { case Def-Use chains are expensive foo(int i, int j) { … switch (i) { case 0: x=3; break; case 1: x=1; break; case 2: x=6; case 3: x=7; default: x = 11; } x 1 is one of the above x’s switch (j) { A case 0: y=x 1+7; case 1: y=x 1+4; case 2: y=x 1 -2; case 3: y=x 1+1; default: y=x 1+9; } CS 745: SSA solution is to limit each var to ONE def site © Seth Copen Goldstein & Todd C. Mowry 2001 -3 6

Advantages of SSA • Makes du-chains explicit • Makes dataflow analysis easier • Improves Advantages of SSA • Makes du-chains explicit • Makes dataflow analysis easier • Improves register allocation – Automatically builds Webs – Makes building interference graphs easier • For most programs reduces space/time requirements CS 745: SSA © Seth Copen Goldstein & Todd C. Mowry 2001 -3 7

SSA • Static single assignment is an IR where every variable is assigned a SSA • Static single assignment is an IR where every variable is assigned a value at most once in the program text • Easy for a basic block: – assign to a fresh variable at each stmt. – each uses the most recently defined var. – (Similar to Value Numbering) CS 745: SSA © Seth Copen Goldstein & Todd C. Mowry 2001 -3 8

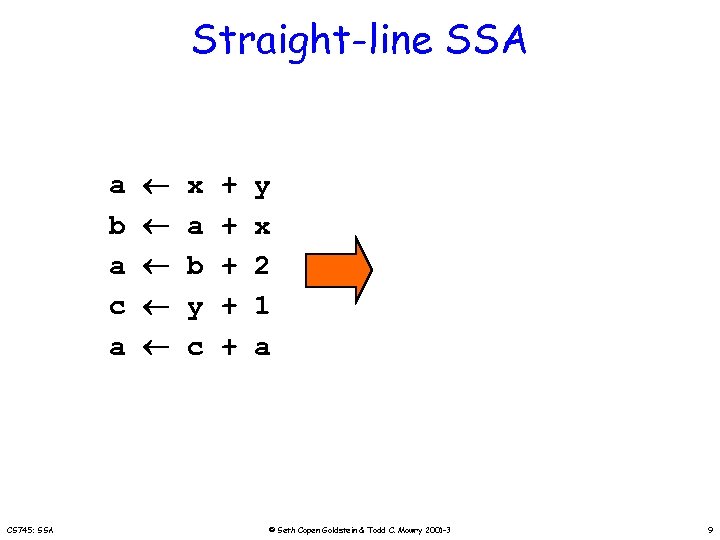Straight-line SSA a b a c a CS 745: SSA x a b y Straight-line SSA a b a c a CS 745: SSA x a b y c + + + y x 2 1 a © Seth Copen Goldstein & Todd C. Mowry 2001 -3 9

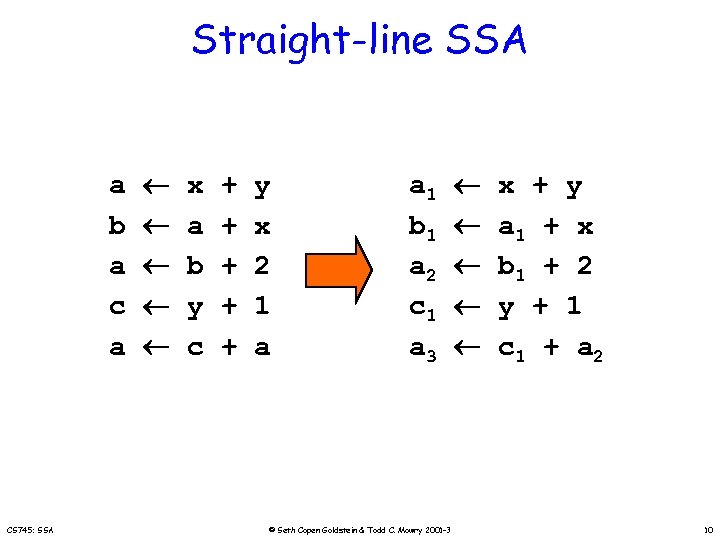Straight-line SSA a b a c a CS 745: SSA x a b y Straight-line SSA a b a c a CS 745: SSA x a b y c + + + y x 2 1 a a 1 b 1 a 2 c 1 a 3 © Seth Copen Goldstein & Todd C. Mowry 2001 -3 x + y a 1 + x b 1 + 2 y + 1 c 1 + a 2 10

SSA • Static single assignment is an IR where every variable is assigned a SSA • Static single assignment is an IR where every variable is assigned a value at most once in the program text • Easy for a basic block: – assign to a fresh variable at each stmt. – each uses the most recently defined var. – (Similar to Value Numbering) • What about at joins in the CFG? CS 745: SSA © Seth Copen Goldstein & Todd C. Mowry 2001 -3 11

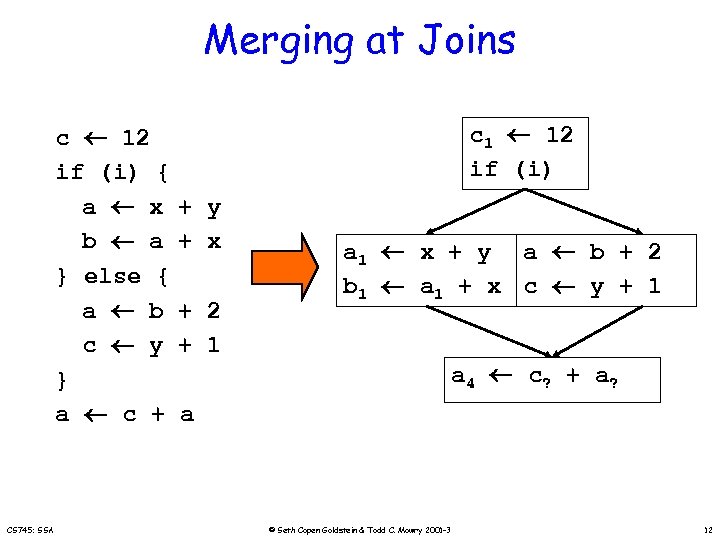Merging at Joins c 12 if (i) { a x b a } else Merging at Joins c 12 if (i) { a x b a } else { a b c y } a c + CS 745: SSA c 1 12 if (i) + y + x + 2 + 1 a 1 x + y a b + 2 b 1 a 1 + x c y + 1 a 4 c ? + a ? a © Seth Copen Goldstein & Todd C. Mowry 2001 -3 12

SSA • Static single assignment is an IR where every variable is assigned a SSA • Static single assignment is an IR where every variable is assigned a value at most once in the program text • Easy for a basic block: – assign to a fresh variable at each stmt. – Each uses the most recently defined var. – (Similar to Value Numbering) • What about at joins in the CFG? – Use a notional fiction: A function CS 745: SSA © Seth Copen Goldstein & Todd C. Mowry 2001 -3 13

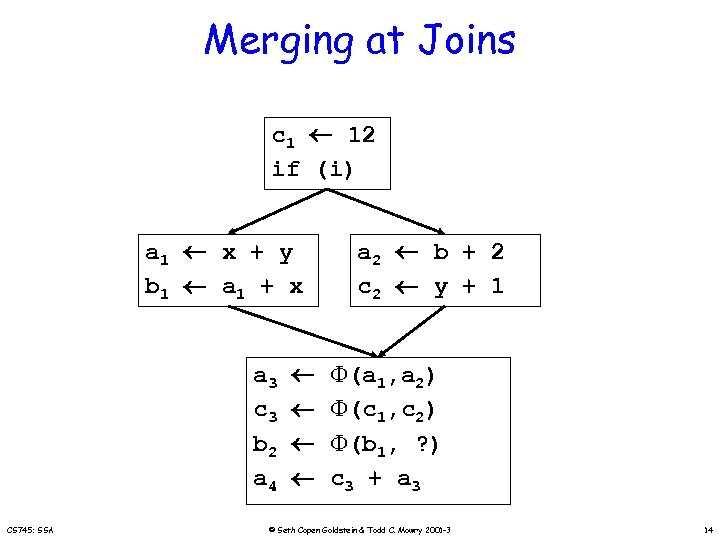Merging at Joins c 1 12 if (i) a 1 x + y b Merging at Joins c 1 12 if (i) a 1 x + y b 1 a 1 + x a 3 c 3 b 2 a 4 CS 745: SSA a 2 b + 2 c 2 y + 1 (a 1, a 2) (c 1, c 2) (b 1, ? ) c 3 + a 3 © Seth Copen Goldstein & Todd C. Mowry 2001 -3 14

The function • merges multiple definitions along multiple control paths into a single definition. The function • merges multiple definitions along multiple control paths into a single definition. • At a BB with p predecessors, there are p arguments to the function. xnew (x 1, … , xp) • How do we choose which xi to use? – We don’t really care! – If we care, use moves on each incoming edge CS 745: SSA © Seth Copen Goldstein & Todd C. Mowry 2001 -3 15

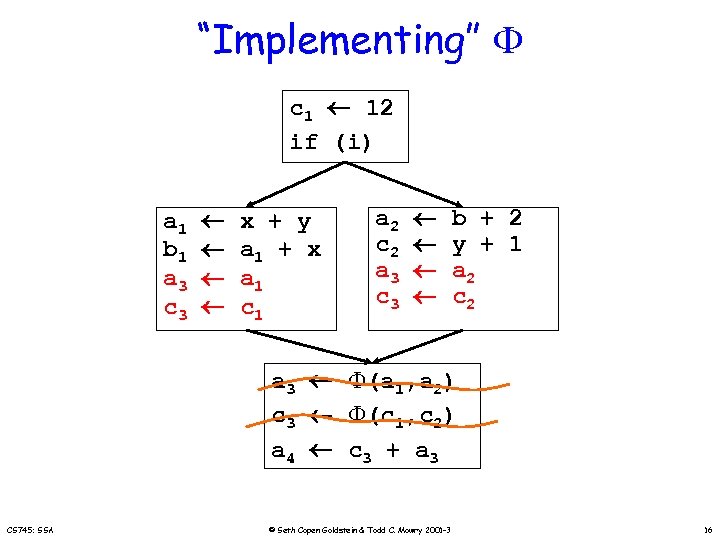“Implementing” c 1 12 if (i) a 1 b 1 a 3 c 3 “Implementing” c 1 12 if (i) a 1 b 1 a 3 c 3 x + y a 1 + x a 1 c 1 a 2 c 2 a 3 c 3 b + 2 y + 1 a 2 c 2 a 3 (a 1, a 2) c 3 (c 1, c 2) a 4 c 3 + a 3 CS 745: SSA © Seth Copen Goldstein & Todd C. Mowry 2001 -3 16

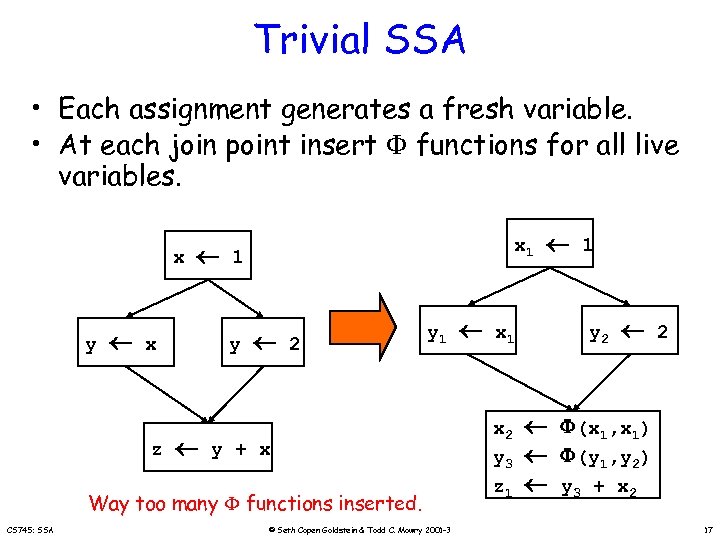Trivial SSA • Each assignment generates a fresh variable. • At each join point Trivial SSA • Each assignment generates a fresh variable. • At each join point insert functions for all live variables. x y x z x 1 1 y 2 y 1 y + x Way too many functions inserted. CS 745: SSA © Seth Copen Goldstein & Todd C. Mowry 2001 -3 x 1 x 2 y 3 z 1 1 y 2 2 (x 1, x 1) (y 1, y 2) y 3 + x 2 17

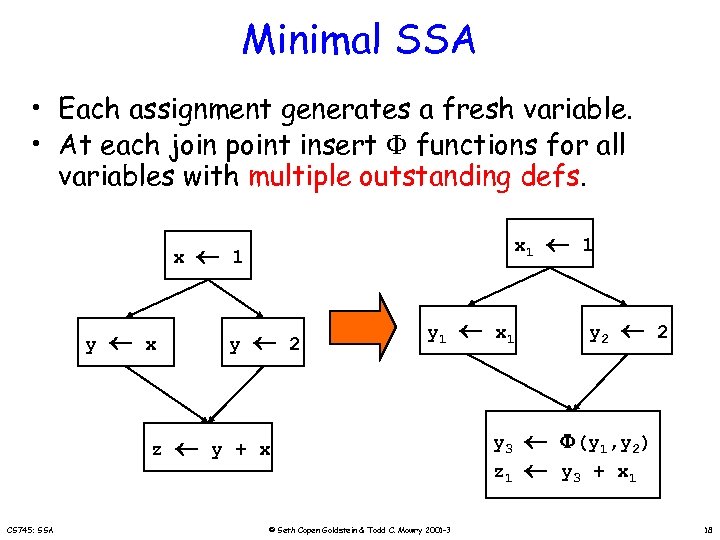Minimal SSA • Each assignment generates a fresh variable. • At each join point Minimal SSA • Each assignment generates a fresh variable. • At each join point insert functions for all variables with multiple outstanding defs. x y x z CS 745: SSA x 1 1 y 2 y 1 y + x © Seth Copen Goldstein & Todd C. Mowry 2001 -3 x 1 y 3 z 1 1 y 2 2 (y 1, y 2) y 3 + x 1 18

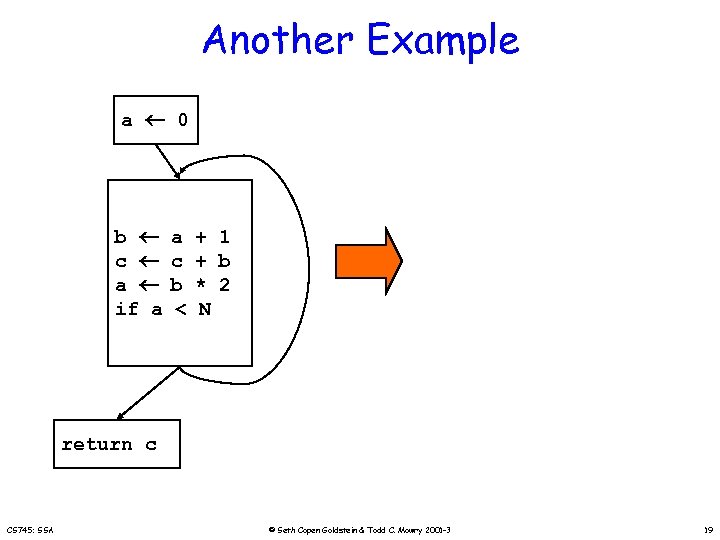Another Example a 0 b c a if a a c b < + Another Example a 0 b c a if a a c b < + 1 + b * 2 N return c CS 745: SSA © Seth Copen Goldstein & Todd C. Mowry 2001 -3 19

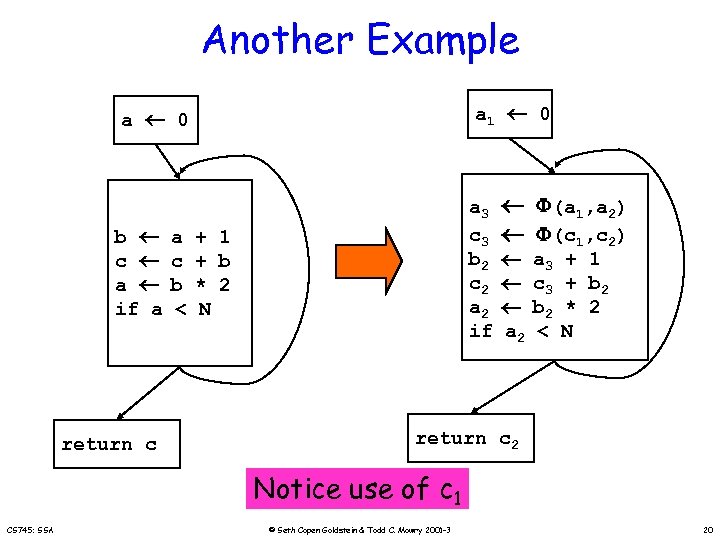Another Example a 0 a 1 0 b c a if a a 3 Another Example a 0 a 1 0 b c a if a a 3 c 3 b 2 c 2 a 2 if return c a c b < + 1 + b * 2 N (a 1, a 2) (c 1, c 2) a 2 a 3 c 3 b 2 < + 1 + b 2 * 2 N return c 2 Notice use of c 1 CS 745: SSA © Seth Copen Goldstein & Todd C. Mowry 2001 -3 20

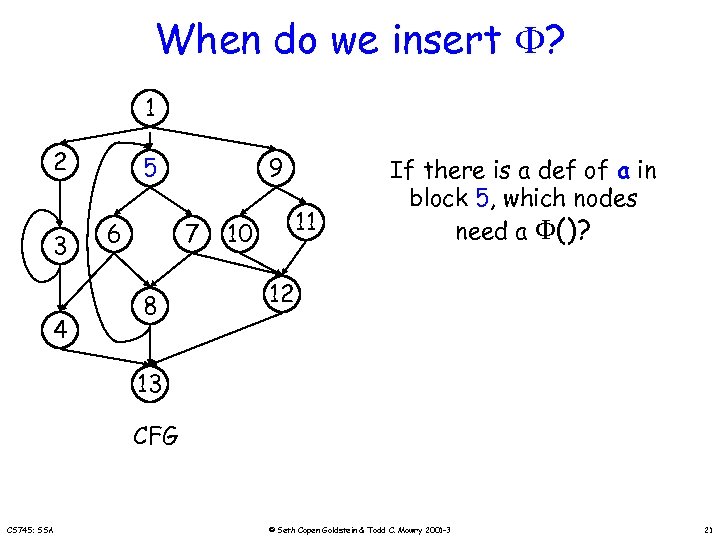When do we insert ? 1 2 3 4 5 6 9 7 8 When do we insert ? 1 2 3 4 5 6 9 7 8 11 10 If there is a def of a in block 5, which nodes need a ()? 12 13 CFG CS 745: SSA © Seth Copen Goldstein & Todd C. Mowry 2001 -3 21

When do we insert ? • We insert a function for variable A in When do we insert ? • We insert a function for variable A in block Z iff: – A was defined more than once before (i. e. , A defined in X and Y AND X Y) – There exists a non-empty path from x to z, Pxz, and a non-empty from y to z, Pyz s. t. • Pxz Pyz = { z } • z Pxq or z Pyr where Pxz = Pxq z and Pyz = Pyr z • Entry block contains an implicit def of all vars • Note: A = (…) is a def of A CS 745: SSA © Seth Copen Goldstein & Todd C. Mowry 2001 -3 22

Dominance Property of SSA • In SSA, definitions dominate uses. – If xi is Dominance Property of SSA • In SSA, definitions dominate uses. – If xi is used in x (…, xi, …), then BB(xi) dominates ith predecessor of BB(PHI) – If x is used in y … x …, then BB(x) dominates BB(y) • We can use this for an efficient algorithm to convert to SSA CS 745: SSA © Seth Copen Goldstein & Todd C. Mowry 2001 -3 23

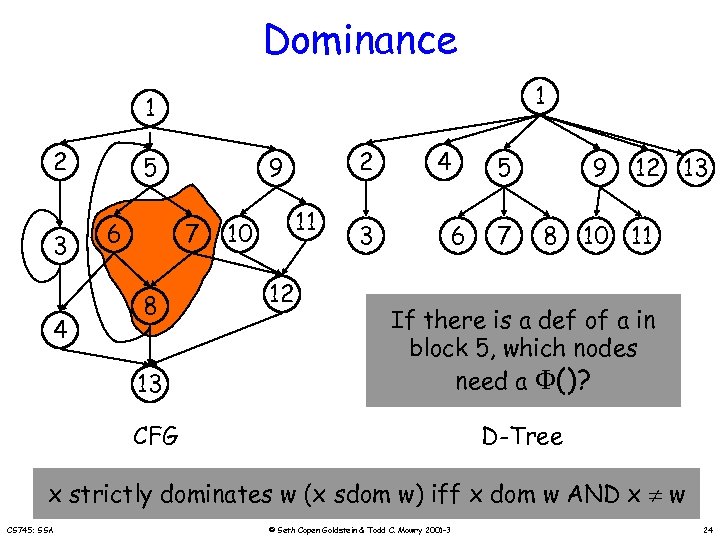Dominance 1 1 2 3 5 6 7 8 2 9 11 10 12 Dominance 1 1 2 3 5 6 7 8 2 9 11 10 12 3 4 6 5 7 9 8 12 13 10 11 13 If there is a def of a in block 5, which nodes need a ()? CFG 4 D-Tree x strictly dominates w (x sdom w) iff x dom w AND x w CS 745: SSA © Seth Copen Goldstein & Todd C. Mowry 2001 -3 24

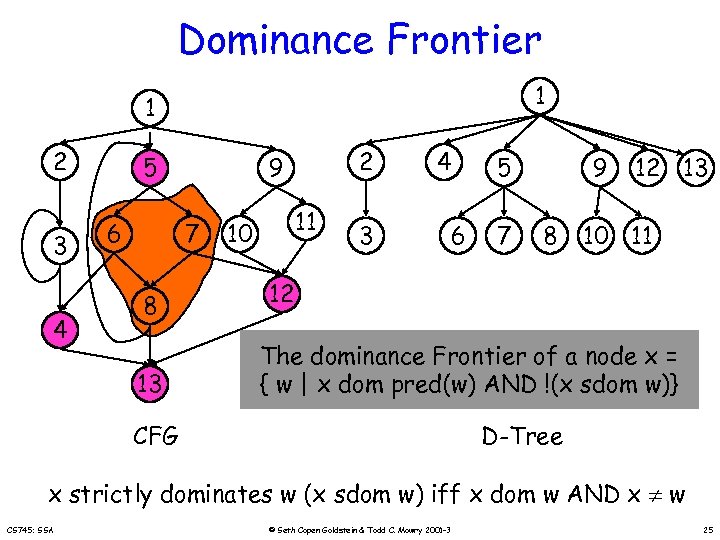Dominance Frontier 1 1 2 3 4 5 6 7 8 13 2 9 Dominance Frontier 1 1 2 3 4 5 6 7 8 13 2 9 11 10 3 4 6 5 7 9 8 12 13 10 11 12 The dominance Frontier of a node x = { w | x dom pred(w) AND !(x sdom w)} CFG D-Tree x strictly dominates w (x sdom w) iff x dom w AND x w CS 745: SSA © Seth Copen Goldstein & Todd C. Mowry 2001 -3 25

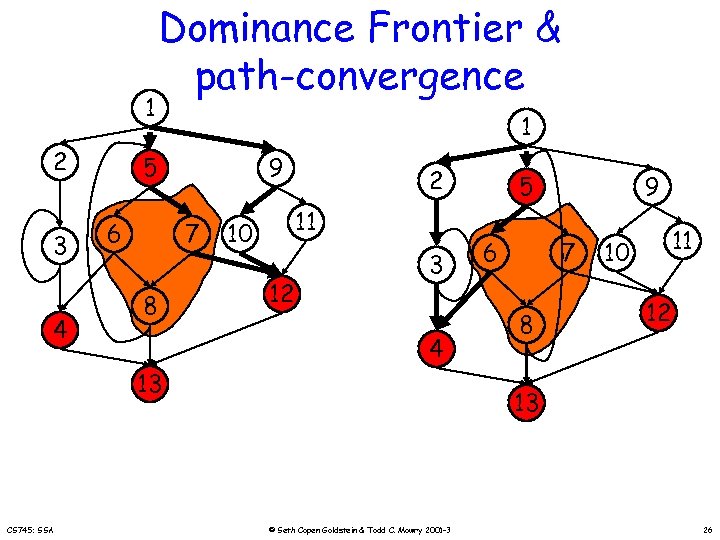1 2 3 4 Dominance Frontier & path-convergence 1 5 6 9 7 8 1 2 3 4 Dominance Frontier & path-convergence 1 5 6 9 7 8 2 11 10 12 3 4 13 CS 745: SSA 5 6 9 7 8 11 10 12 13 © Seth Copen Goldstein & Todd C. Mowry 2001 -3 26

Using DF to compute SSA • place all () • Rename all variables CS Using DF to compute SSA • place all () • Rename all variables CS 745: SSA © Seth Copen Goldstein & Todd C. Mowry 2001 -3 27

Using DF to Place () • Gather all the defsites of every variable • Using DF to Place () • Gather all the defsites of every variable • Then, for every variable – foreach defsite • foreach node in DF(defsite) – if we haven’t put () in node put one in – If this node didn’t define the variable before: add this node to the defsites • This essentially computes the Iterated Dominance Frontier on the fly, inserting the minimal number of () neccesary CS 745: SSA © Seth Copen Goldstein & Todd C. Mowry 2001 -3 28

Using DF to Place () foreach node n { foreach variable v defined in Using DF to Place () foreach node n { foreach variable v defined in n { orig[n] = {v} defsites[v] = {n} } } foreach variable v { W = defsites[v] while W not empty { n = remove node from W foreach y in DF[n] if y PHI[v] { insert “v (v, v, …)” at top of y PHI[v] = PHI[v] {y} if v orig[y]: W = W {y} } CS 745: SSA © Seth Copen Goldstein & Todd C. Mowry 2001 -3 29

Renaming Variables • Walk the D-tree, renaming variables as you go • Replace uses Renaming Variables • Walk the D-tree, renaming variables as you go • Replace uses with more recent renamed def – For straight-line code this is easy – If there are branches and joins? CS 745: SSA © Seth Copen Goldstein & Todd C. Mowry 2001 -3 30

Renaming Variables • Walk the D-tree, renaming variables as you go • Replace uses Renaming Variables • Walk the D-tree, renaming variables as you go • Replace uses with more recent renamed def – For straight-line code this is easy – If there are branches and joins use the closest def such that the def is above the use in the D-tree • Easy implementation: – for each var: rename (v) – rename(v): replace uses with top of stack at def: push onto stack call rename(v) on all children in D-tree for each def in this block pop from stack CS 745: SSA © Seth Copen Goldstein & Todd C. Mowry 2001 -3 31

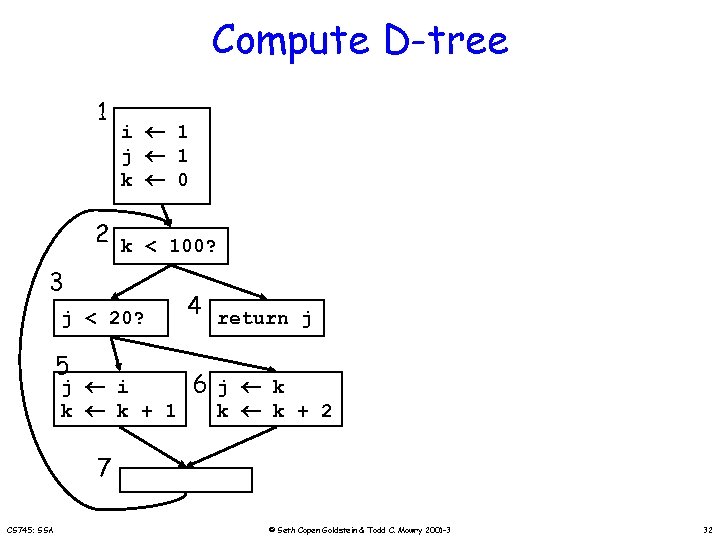Compute D-tree 1 i 1 j 1 k 0 2 k < 100? 3 Compute D-tree 1 i 1 j 1 k 0 2 k < 100? 3 j < 20? 5 j i k k + 1 4 return j 6 j k k k + 2 7 CS 745: SSA © Seth Copen Goldstein & Todd C. Mowry 2001 -3 32

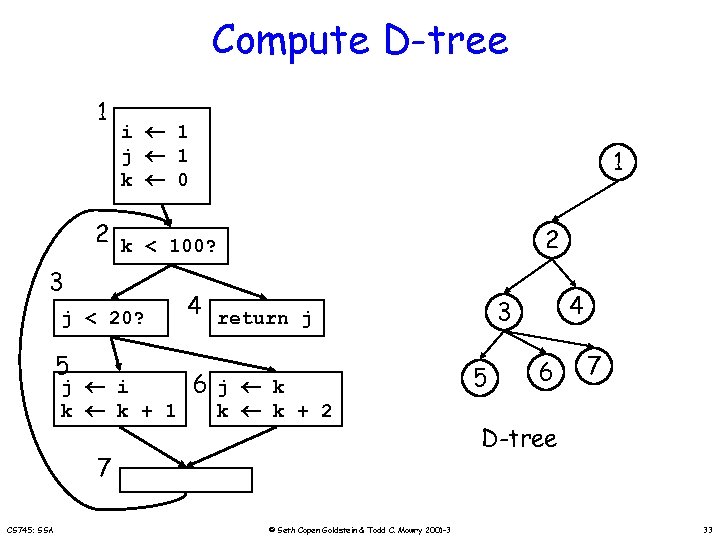Compute D-tree 1 i 1 j 1 k 0 1 2 k < 100? Compute D-tree 1 i 1 j 1 k 0 1 2 k < 100? 3 j < 20? 5 j i k k + 1 2 4 return j 6 j k k k + 2 7 CS 745: SSA © Seth Copen Goldstein & Todd C. Mowry 2001 -3 4 3 5 6 7 D-tree 33

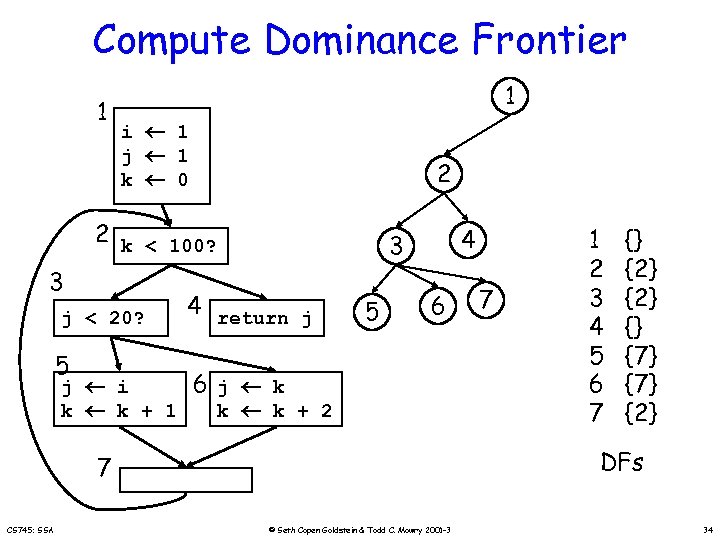Compute Dominance Frontier 1 1 i 1 j 1 k 0 2 2 k Compute Dominance Frontier 1 1 i 1 j 1 k 0 2 2 k < 100? 3 j < 20? 5 j i k k + 1 4 3 4 return j 5 6 6 j k k k + 2 {} {2} {} {7} {2} DFs 7 CS 745: SSA 7 1 2 3 4 5 6 7 © Seth Copen Goldstein & Todd C. Mowry 2001 -3 34

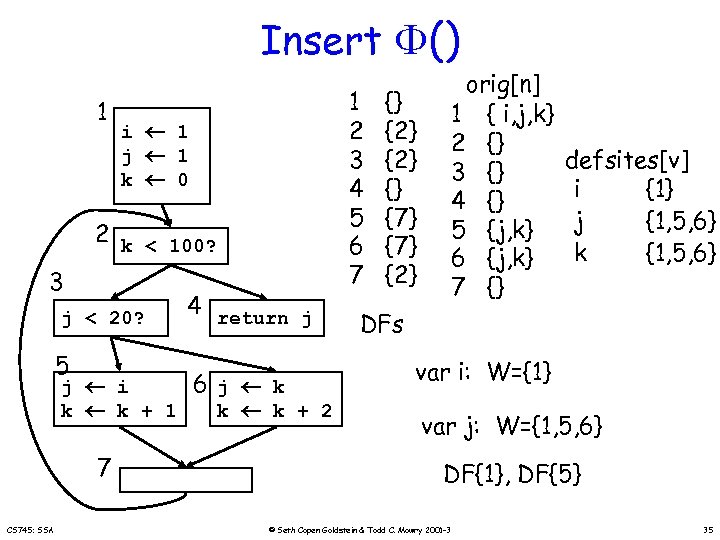Insert () 1 i 1 j 1 k 0 2 k < 100? 3 Insert () 1 i 1 j 1 k 0 2 k < 100? 3 j < 20? 5 j i k k + 1 7 CS 745: SSA 4 return j 6 j k k k + 2 1 2 3 4 5 6 7 {} {2} {} {7} {2} orig[n] 1 { i, j, k} 2 {} 3 {} 4 {} 5 {j, k} 6 {j, k} 7 {} defsites[v] i {1} j {1, 5, 6} k {1, 5, 6} DFs var i: W={1} var j: W={1, 5, 6} DF{1}, DF{5} © Seth Copen Goldstein & Todd C. Mowry 2001 -3 35

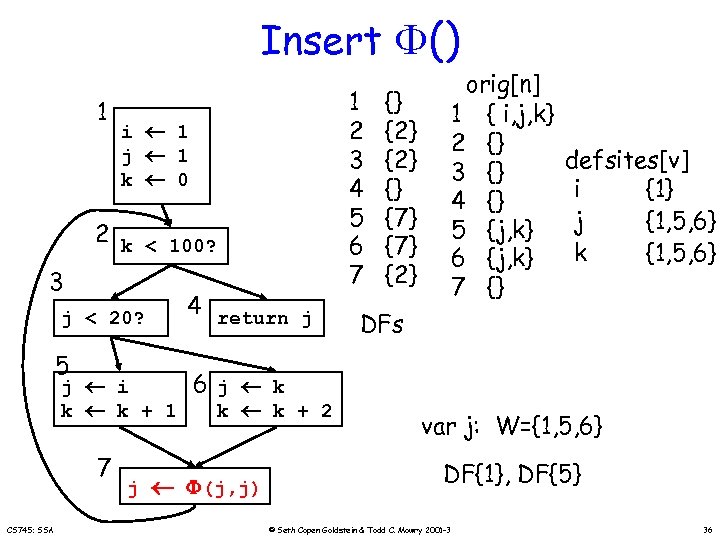Insert () 1 i 1 j 1 k 0 2 k < 100? 3 Insert () 1 i 1 j 1 k 0 2 k < 100? 3 4 return j j < 20? 5 j i k k + 1 7 CS 745: SSA j 1 2 3 4 5 6 7 {} {2} {} {7} {2} orig[n] 1 { i, j, k} 2 {} 3 {} 4 {} 5 {j, k} 6 {j, k} 7 {} defsites[v] i {1} j {1, 5, 6} k {1, 5, 6} DFs 6 j k k k + 2 (j, j) var j: W={1, 5, 6} DF{1}, DF{5} © Seth Copen Goldstein & Todd C. Mowry 2001 -3 36

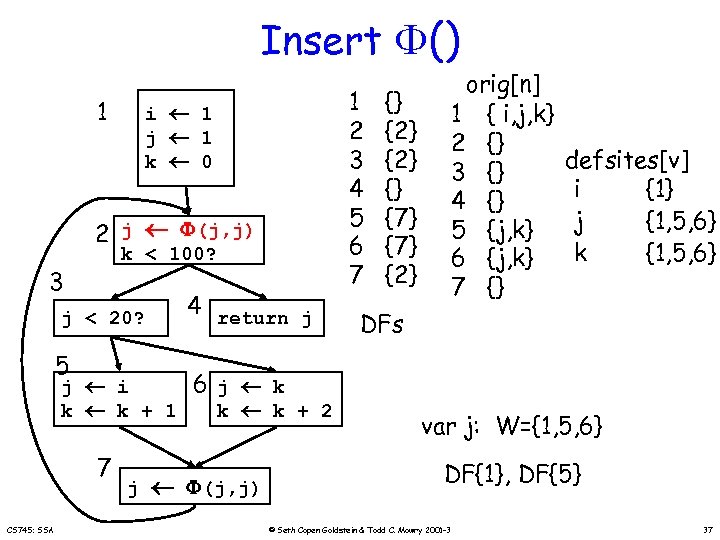Insert () 1 i 1 j 1 k 0 2 j (j, j) k Insert () 1 i 1 j 1 k 0 2 j (j, j) k < 100? 3 4 return j j < 20? 5 j i k k + 1 7 CS 745: SSA j 1 2 3 4 5 6 7 {} {2} {} {7} {2} orig[n] 1 { i, j, k} 2 {} 3 {} 4 {} 5 {j, k} 6 {j, k} 7 {} defsites[v] i {1} j {1, 5, 6} k {1, 5, 6} DFs 6 j k k k + 2 (j, j) var j: W={1, 5, 6} DF{1}, DF{5} © Seth Copen Goldstein & Todd C. Mowry 2001 -3 37

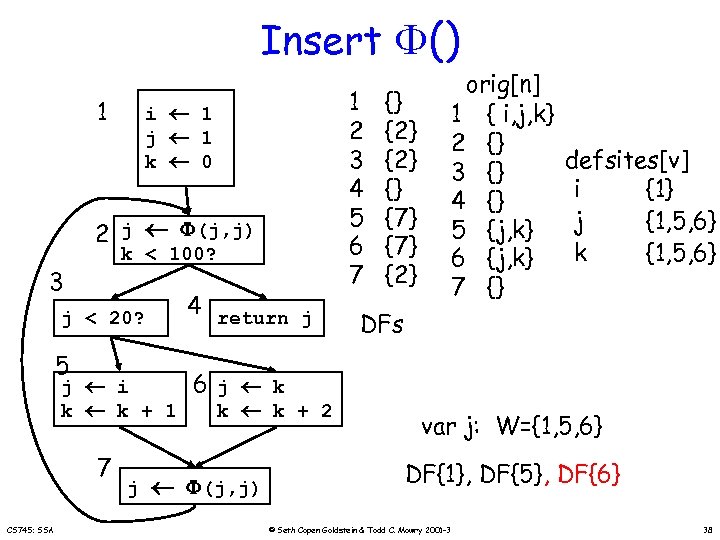Insert () 1 i 1 j 1 k 0 2 j (j, j) k Insert () 1 i 1 j 1 k 0 2 j (j, j) k < 100? 3 4 return j j < 20? 5 j i k k + 1 7 CS 745: SSA j 1 2 3 4 5 6 7 {} {2} {} {7} {2} orig[n] 1 { i, j, k} 2 {} 3 {} 4 {} 5 {j, k} 6 {j, k} 7 {} defsites[v] i {1} j {1, 5, 6} k {1, 5, 6} DFs 6 j k k k + 2 (j, j) var j: W={1, 5, 6} DF{1}, DF{5}, DF{6} © Seth Copen Goldstein & Todd C. Mowry 2001 -3 38

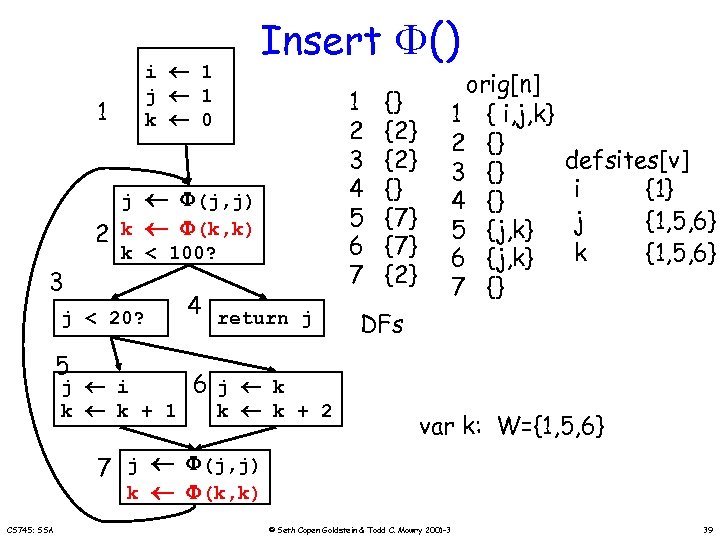1 2 3 i 1 j 1 k 0 j (j, j) k (k, 1 2 3 i 1 j 1 k 0 j (j, j) k (k, k) k < 100? j < 20? 5 Insert () j i k k + 1 4 return j 1 2 3 4 5 6 7 {} {2} {} {7} {2} orig[n] 1 { i, j, k} 2 {} 3 {} 4 {} 5 {j, k} 6 {j, k} 7 {} defsites[v] i {1} j {1, 5, 6} k {1, 5, 6} DFs 6 j k k k + 2 var k: W={1, 5, 6} 7 j (j, j) k (k, k) CS 745: SSA © Seth Copen Goldstein & Todd C. Mowry 2001 -3 39

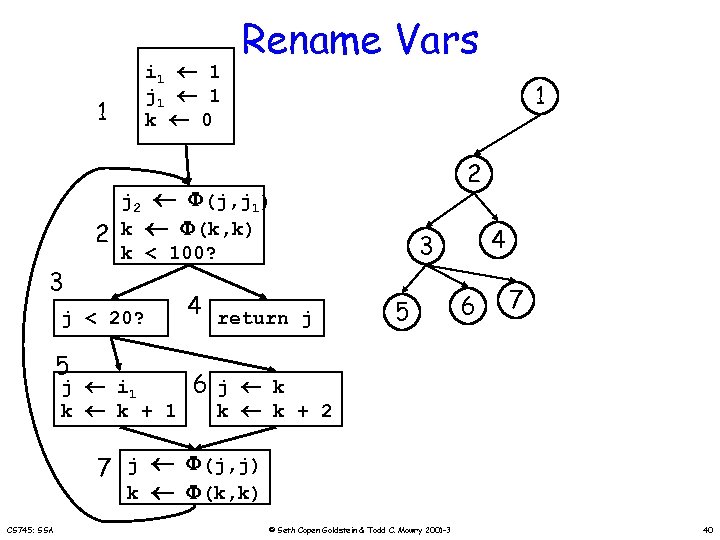1 2 3 i 1 1 j 1 1 k 0 1 2 j 1 2 3 i 1 1 j 1 1 k 0 1 2 j 2 (j, j 1) k (k, k) k < 100? j < 20? 5 Rename Vars j i 1 k k + 1 4 return j 4 3 5 6 7 6 j k k k + 2 7 j (j, j) k (k, k) CS 745: SSA © Seth Copen Goldstein & Todd C. Mowry 2001 -3 40

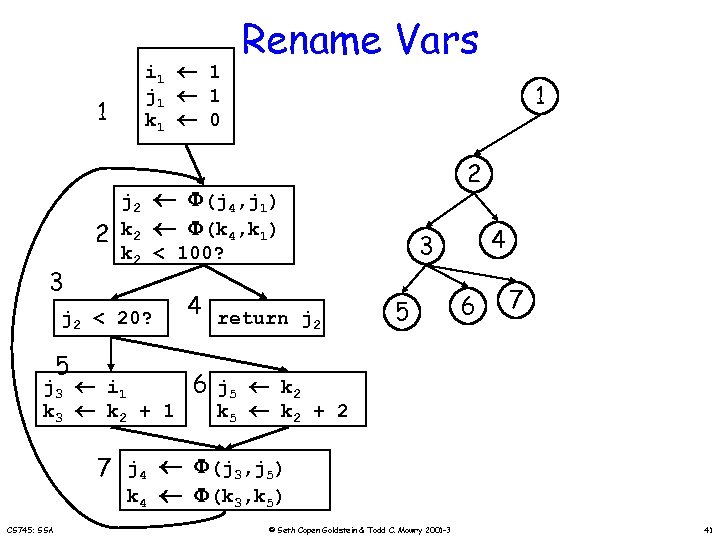1 2 3 i 1 1 j 1 1 k 1 0 1 2 1 2 3 i 1 1 j 1 1 k 1 0 1 2 j 2 (j 4, j 1) k 2 (k 4, k 1) k 2 < 100? j 2 < 20? 5 Rename Vars j 3 i 1 k 3 k 2 + 1 4 return j 2 4 3 5 6 7 6 j 5 k 2 k 5 k 2 + 2 7 j 4 (j 3, j 5) k 4 (k 3, k 5) CS 745: SSA © Seth Copen Goldstein & Todd C. Mowry 2001 -3 41

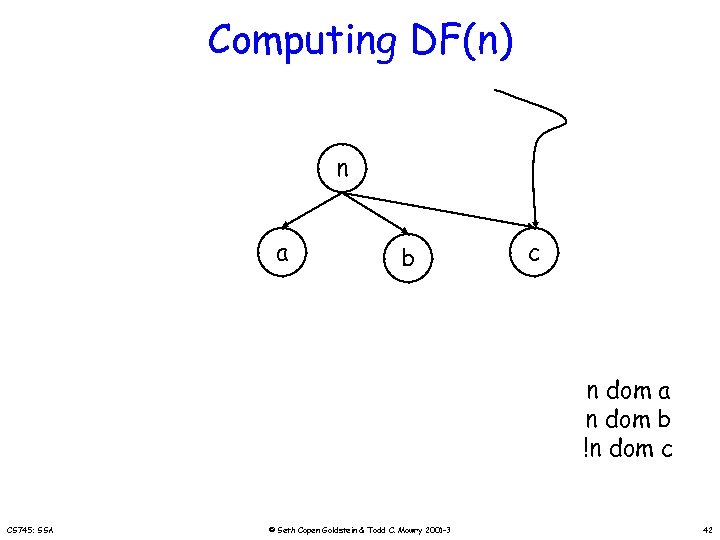Computing DF(n) n a b c n dom a n dom b !n dom Computing DF(n) n a b c n dom a n dom b !n dom c CS 745: SSA © Seth Copen Goldstein & Todd C. Mowry 2001 -3 42

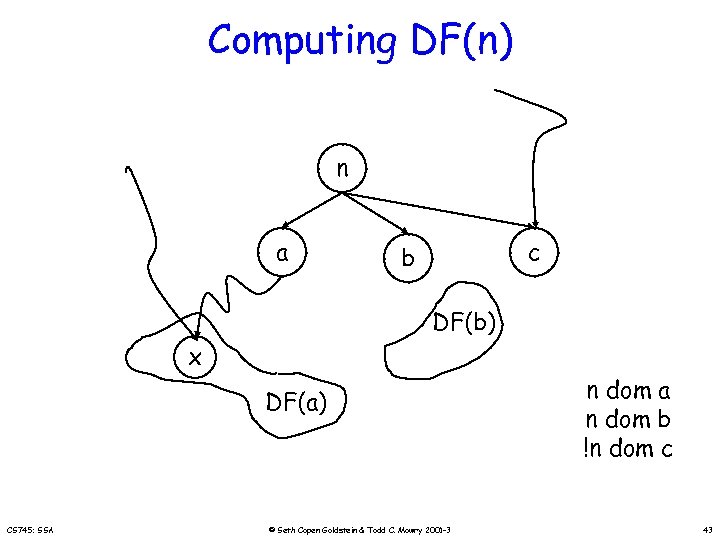Computing DF(n) n a c b DF(b) x DF(a) CS 745: SSA © Seth Computing DF(n) n a c b DF(b) x DF(a) CS 745: SSA © Seth Copen Goldstein & Todd C. Mowry 2001 -3 n dom a n dom b !n dom c 43

Computing the Dominance Frontier The dominance Frontier of a node x = { w Computing the Dominance Frontier The dominance Frontier of a node x = { w | x dom pred(w) AND !(x sdom w)} compute-DF(n) S = {} foreach node y in succ[n] if idom(y) n S=S {y} foreach child of n, c, in D-tree compute-DF(c) foreach w in DF[c] if !n dom w S=S {w} DF[n] = S CS 745: SSA © Seth Copen Goldstein & Todd C. Mowry 2001 -3 44

SSA Properties • Only 1 assignment per variable • definitions dominate uses CS 745: SSA Properties • Only 1 assignment per variable • definitions dominate uses CS 745: SSA © Seth Copen Goldstein & Todd C. Mowry 2001 -3 45