14. 8 Jacobians For more interesting illustrations of this topic, visit http: //www. math. umn. edu/~rogness/multivar/nonlineartransformation. html
Definition of the Jacobian
Example 1 Find the Jacobian for the change of variables x = r cosө and y = r sinө
Example 1 Solution Find the Jacobian for the change of variables x = r cosө and y = r sinө
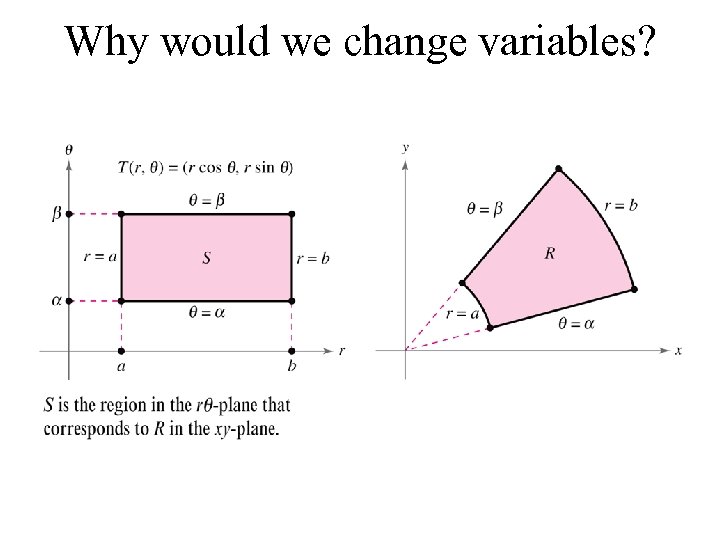
Why would we change variables?
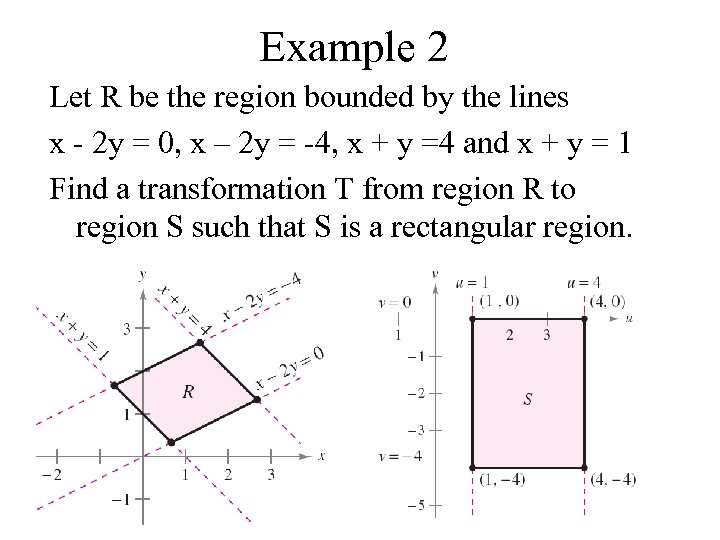
Example 2 Let R be the region bounded by the lines x - 2 y = 0, x – 2 y = -4, x + y =4 and x + y = 1 Find a transformation T from region R to region S such that S is a rectangular region.
Example: 2 Solution
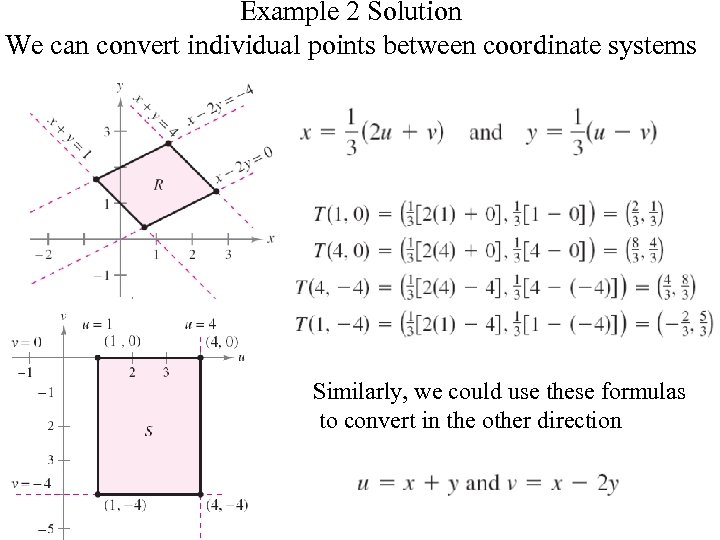
Example 2 Solution We can convert individual points between coordinate systems Similarly, we could use these formulas to convert in the other direction
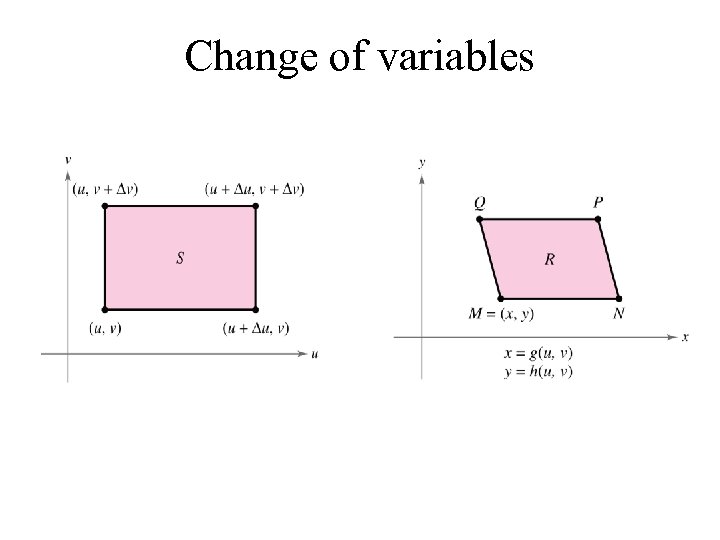
Change of variables
Example 3 use a change of variables to simplify a region Let R be the region bounded by the lines x - 2 y = 0, x – 2 y = -4, x + y =4 and x + y = 1 as shown below. Evaluate the double integral.
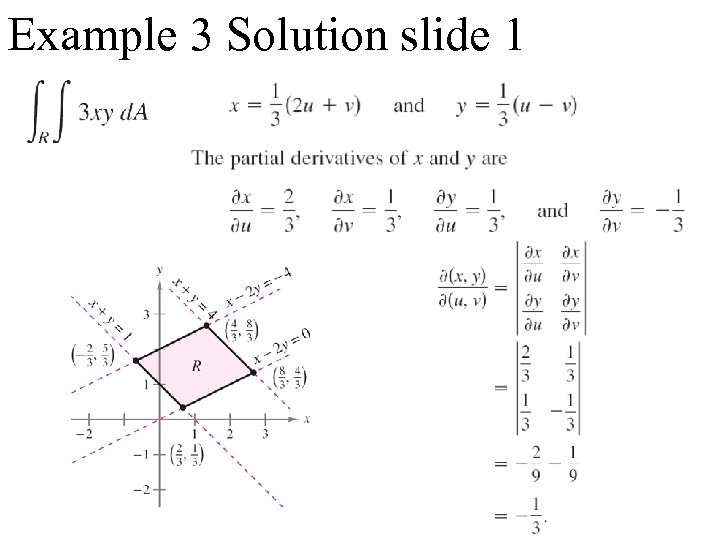
Example 3 Solution slide 1
Example 3 Solution slide 2
Example 4 Let R be the region bounded by vertices (0, 1), (1, 2) (2, 1), (1, 0) a) Sketch the transformed region b) Evaluate the integral
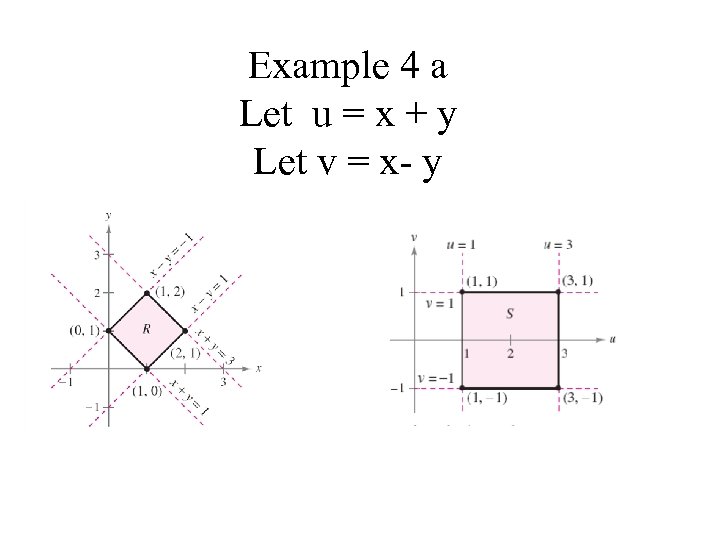
Example 4 a Let u = x + y Let v = x- y
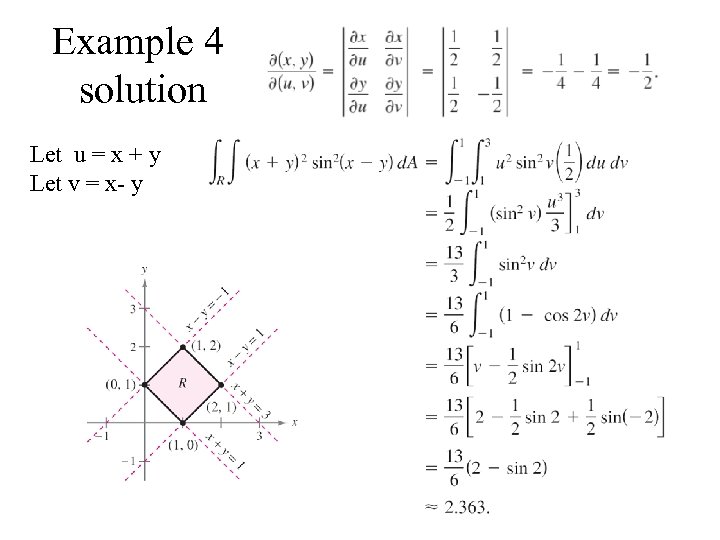
Example 4 solution Let u = x + y Let v = x- y
Wisdom from Singapore: Explaining a joke is like dissecting a frog. You learn more about it but you kill it in the process. -Niel Chong
Скачать презентацию 14 8 Jacobians For more interesting illustrations of
302830ec8b14f4638bf50d974df82311.ppt