14 02 2012 Урок 1 Цели урока

14. 02. 2012 Урок 1

Цели урока • Ввести понятие многогранника и его элементов. • Ввести понятие призмы и ее элементов.

П А Р А Л Л Е П И П Е Д ТЕТРАЭДР НАКЛОННЫЙ ОКТАЭДР ПРЯМОУГОЛЬНЫЙ

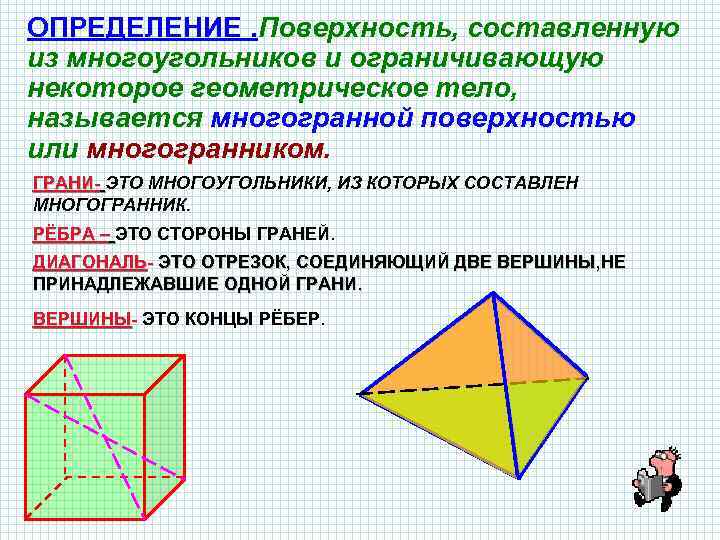ОПРЕДЕЛЕНИЕ. Поверхность, составленную из многоугольников и ограничивающую некоторое геометрическое тело, называется многогранной поверхностью или многогранником. ГРАНИ- ЭТО МНОГОУГОЛЬНИКИ, ИЗ КОТОРЫХ СОСТАВЛЕН МНОГОГРАННИК. РЁБРА – ЭТО СТОРОНЫ ГРАНЕЙ. ДИАГОНАЛЬ- ЭТО ОТРЕЗОК, СОЕДИНЯЮЩИЙ ДВЕ ВЕРШИНЫ, НЕ ПРИНАДЛЕЖАВШИЕ ОДНОЙ ГРАНИ. ВЕРШИНЫ- ЭТО КОНЦЫ РЁБЕР.

ПРАВИЛЬНЫЙ МНОГОГРАННИКвыпуклый многогранник, грани которого являются правильными многоугольниками с одним и тем же числом сторон и в каждой вершине которого сходится одно и то же число ребер. Икосаэдр Тетраэдр Октаэдр Гексаэдр Додекаэдр

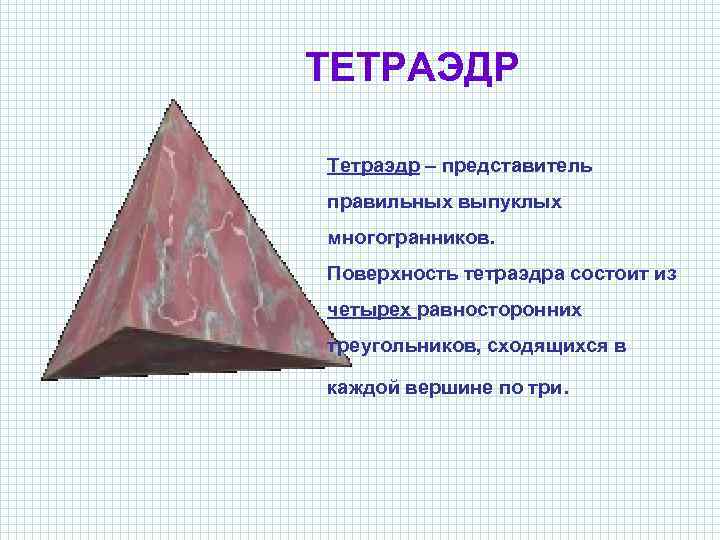ТЕТРАЭДР Тетраэдр – представитель правильных выпуклых многогранников. Поверхность тетраэдра состоит из четырех равносторонних треугольников, сходящихся в каждой вершине по три.

КУБ (ГЕКСАЭДР) Куб или гексаэдр – представитель правильных выпуклых многогранников. Куб имеет шесть квадратных граней, сходящихся в каждой вершине по три.

ОКТАЭДР Октаэдр – представитель семейства правильных выпуклых многогранников. Октаэдр имеет восемь треугольных граней, сходящихся в каждой вершине по четыре.

ДОДЕКАЭДР Додекаэдр – представитель семейства правильных выпуклых многогранников. Додекаэдр имеет двенадцать пятиугольных граней, сходящихся в вершинах по три.

ИКОСАЭДР Икосаэдр – представитель семейства правильных выпуклых многогранников. Поверхность икосаэдра состоит из двадцати равносторонних треугольников, сходящихся в каждой вершине по пять.

«эдра» - грань «тетра» - 4 «гекса» - 6 «окта» - 8 «икоса» - 20 «додека» - 12

МНОГОГРАННИКИ БЫВАЮТ ВЫПУКЛЫЕ И НЕВЫПУКЛЫЕ. МНОГОГРАННИК НАЗЫВАЕТСЯ ВЫПУКЛЫМ, ЕСЛИ ОН РАСПОЛОЖЕН ПО ОДНУ СТОРОНУ ОТ ПЛОСКОСТИ КАЖДОЙ ЕГО ГРАНИ. ВЫПУКЛЫЕ НЕВЫПУКЛЫЕ

В выпуклом многограннике сумма всех плоских углов при каждой его вершине меньше 360

Эйлерова характеристика Число вершин минус число рёбер плюс число граней равно двум. В – Р + Г = 2 № Наименование многогранника В Р Г Эйлерова характеристика 1 Тетраэдр 4 6 4 4 -6+4=2 2 Параллелепипед 8 12 6 8 -12+6=2 3 Куб 8 12 6 8 -12+6=2 4 n-угольная пирамида n+1 2 n n+1 (n+1)-2 n+(n+1)=2 5 n-угольная призма 2 n 3 n n+2 2 n-3 n+(n+2)=2

Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук. Л. Кэррол

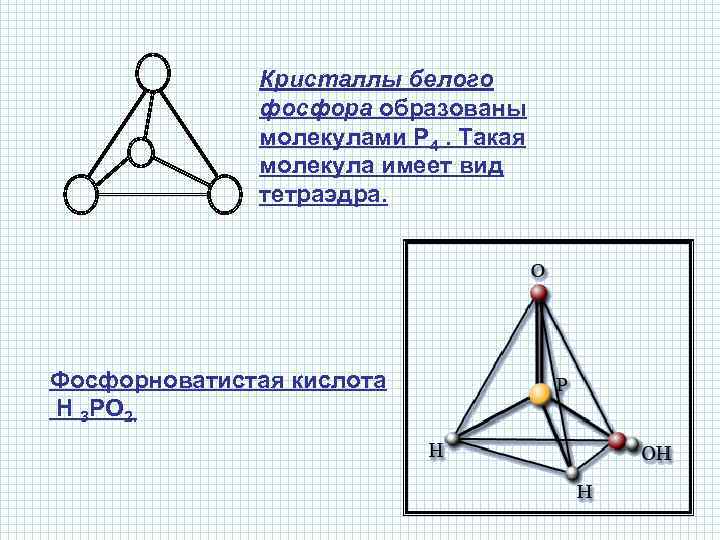Кристаллы белого фосфора образованы молекулами Р 4. Такая молекула имеет вид тетраэдра. Фосфорноватистая кислота Н 3 РО 2.

Кристаллы

Молекулы зеркальных изомеров молочной кислоты.

Строение молекулы метана.

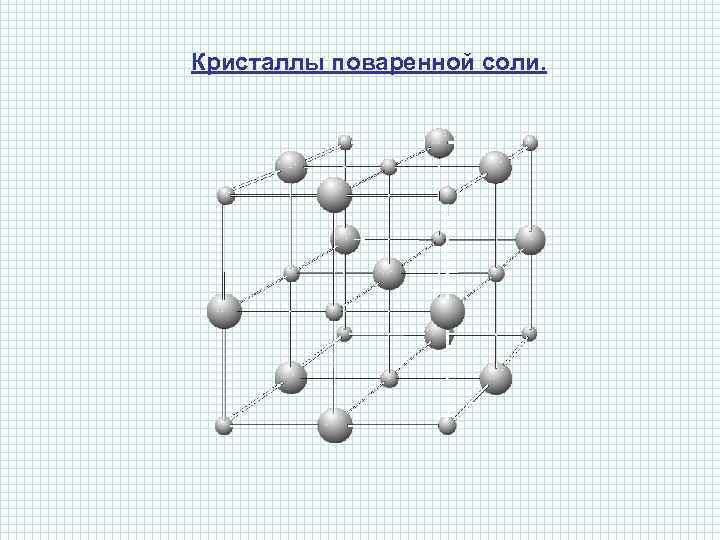Кристаллы поваренной соли.

Строение решетки алмаза.

Вирус полиомиелита имеет форму додекаэдра.

Феодария (Circjgjnia icosahtdra)

«Тайняя вечеря» С. Дали

ГРАВЮРА ГОЛАНДСКОГО ХУДОЖНИКА МАУРИЦА КОРНЕЛИУСА ЭШЕРА «СИЛЫ ГРАВИТАЦИИ»

Правильная форма алмаза.

Леонардо да Винчи любил изготовлять из дерева каркасы правильных многогранников и преподносить их в виде подарка различным знаменитостям.

Удивительно разнообразен мир кристаллов, являющихся природными многогранниками. Кристаллы встречаются повсюду. Мы ходим по кристаллам, строим из кристаллов, обрабатываем кристаллы на заводах, выращиваем кристаллы в лабораториях и в заводских условиях, создаем приборы и изделия из кристаллов, широко применяем кристаллы в науке и технике, едим кристаллы, лечимся кристаллами, находим кристаллы в живых организмах, проникаем в тайны строения кристаллов, выходим на просторы космических дорог с помощью приборов из кристаллов и растим кристаллы в домашних условиях. Подтверждением тому служит форма некоторых кристаллов. Взять хотя бы поваренную соль, без которой мы не можем обойтись. Известно, что она хорошо растворима в воде, служит проводником электрического тока. А кристаллы поваренной соли (Na. Cl) имеют форму куба. В разных химических реакциях применяется сурьменистый сернокислый натрий (Na 5(Sb. O 4(SO 4)) – вещество, синтезированное учеными. Кристалл сурьменистого сернокислого натрия имеет форму тетраэдра.

Кристаллом (от греч. krystallos – «прозрачный лед» ) вначале называли прозрачный кварц (горный хрусталь), встречавшийся в Альпах. Горный хрусталь принимали за лед, затвердевший от холода до такой степени, что он уже не плавится. Кристалл горного хрусталя напоминает оточенный с двух сторон карандаш, т. е. имеет форму шестигранной призмы, на основания которой поставлены шестигранные пирамиды. Исландский шпат имеет форму косого параллелепипеда. Кристалл граната имеет форму ромбододекаэдра (двенадцатигранник, у которого все грани ромбы). Алмаз кристаллизуется в кубической системе (сингонии). Кристаллы алмаза представляют собой гигантские полимерные молекулы и обычно имеют форму октаэдров, ромбододекаэдров, реже – кубов или тетраэдров. АЛМАЗ

Различные геометрические формы находят свое отражение практически во всех отраслях знаний: архитектура, искусств. Маяк был построен на маленьком острове Фарос в Средиземном море, около берегов Александрии. Этот оживленный порт основал Александр Великий во время посещения Египта. Сооружение назвали В III веке до н. э. был построен маяк, по имени острова. На чтобы корабли могли благополучно его строительство, миновать рифы на пути в должно быть, ушло 20 александрийскую бухту. Ночью им лет, а завершен он был помогало в этом отражение языков около 280 г. до н. э. , во времена правления пламени, а днем - столб дыма. Это был первый в мире маяк, и простоял Птолемея II, царя Египта. он 1500 лет.

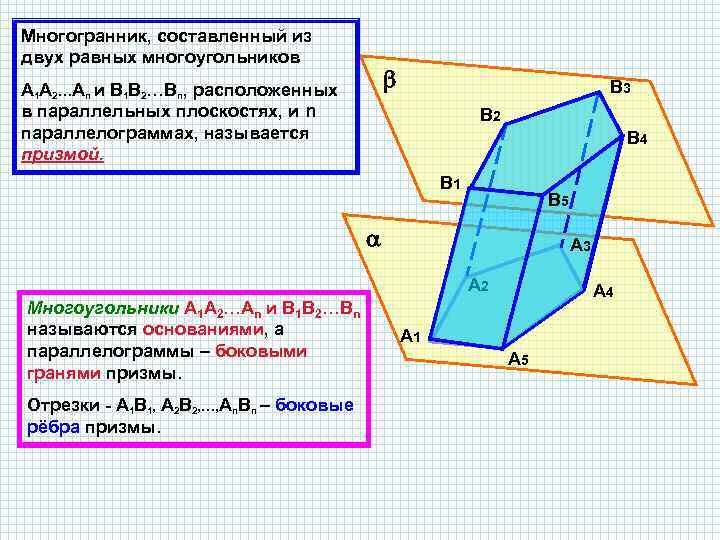Многогранник, составленный из двух равных многоугольников А 1 А 2…Аn и В 1 В 2…Вn, расположенных в параллельных плоскостях, и n параллелограммах, называется призмой. В 3 В 2 В 4 В 1 В 5 А 3 А 2 Многоугольники А 1 А 2…Аn и В 1 В 2…Вn называются основаниями, а параллелограммы – боковыми гранями призмы. Отрезки - А 1 В 1, А 2 В 2, …, Аn. Вn – боковые рёбра призмы. А 4 А 1 А 5

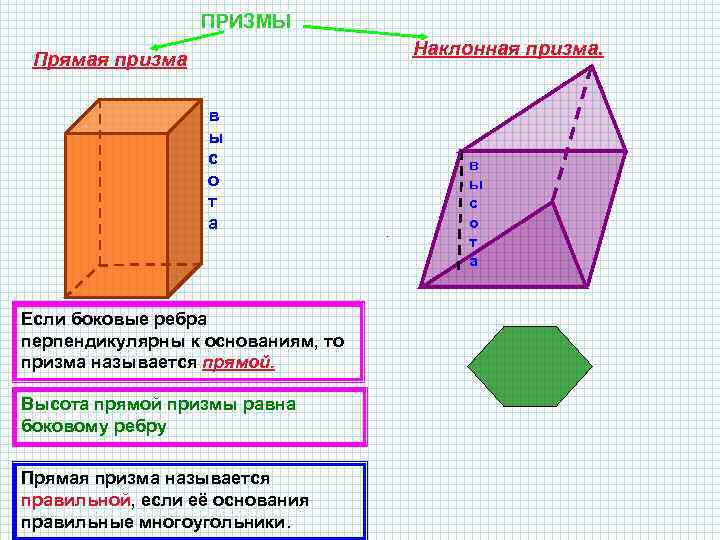ПРИЗМЫ Наклонная призма. Прямая призма в ы с о т а Если боковые ребра перпендикулярны к основаниям, то призма называется прямой. Высота прямой призмы равна боковому ребру Прямая призма называется правильной, если её основания правильные многоугольники. в ы с о т а

Призма Bn B 1 B 3 B 2 Аn Многогранник, составленный из двух равных многоугольников А 1 А 2…Аn и В 1 В 2…Вn, расположенных в параллельных плоскостях, и n параллелограммов, называется призмой. n-угольная призма. А 1 А 3 А 2 Многоугольники А 1 А 2…Аn и В 1 В 2…Вn – основания призмы Параллелограммы

Отрезки А 1 В 1, А 2 В 2 и т. д. - боковые ребра призмы Призма Bn Перпендикуляр, проведенный из какой. B 3 нибудь точки одного основания к плоскости другого основания, называется высотой призмы B 1 B 2 Аn А 1 А 3 А 2

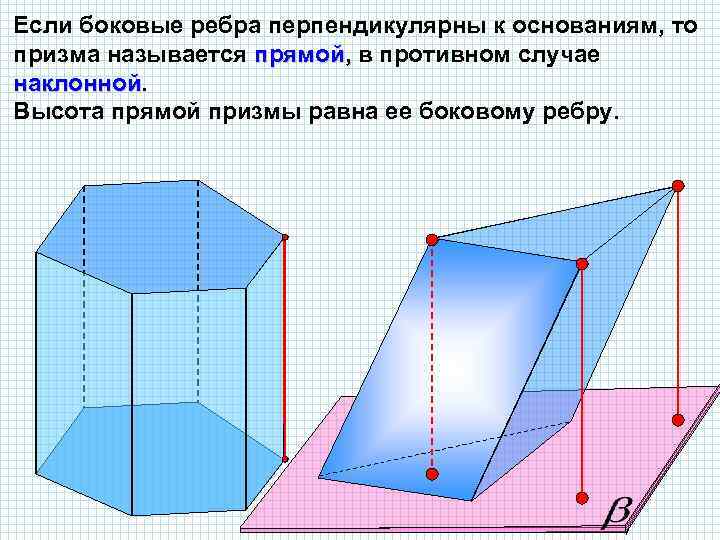Если боковые ребра перпендикулярны к основаниям, то призма называется прямой, в противном случае , наклонной Высота прямой призмы равна ее боковому ребру.

Прямая призма называется правильной, если ее , основания - правильные многоугольники. У такой призмы все боковые грани – равные прямоугольники.

Площадью полной поверхности призмы называется сумма площадей всех граней, а площадью боковой поверхности призмы – площадью боковой поверхности призмы сумма площадей ее боковых граней. h Pocн

Выполнение упражнений 219 х см 45 5 см 12 см

220 Выполнение упражнений В 1 А 1 С 1 D 1 В А С D Дано: АВСDA 1 B 1 C 1 D 1 – прямой параллелепипед, АВСD – ромб, ВD = 10 см, АС = 24 см, ВВ 1 = 10 см. Найти: большую диагональ параллелепипеда.

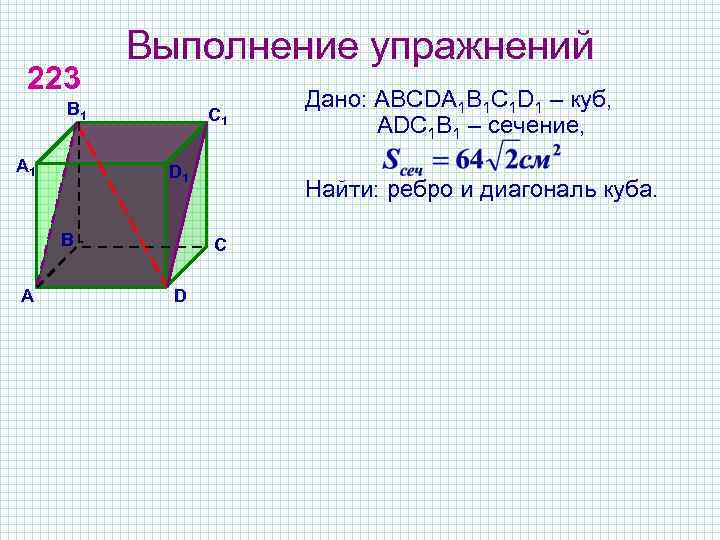223 Выполнение упражнений В 1 А 1 С 1 D 1 В А Найти: ребро и диагональ куба. С D Дано: АВСDA 1 B 1 C 1 D 1 – куб, АDС 1 В 1 – сечение,

Домашнее задание п. 25 , 30, по развертке изготовить многоугольники ( не менее 3)

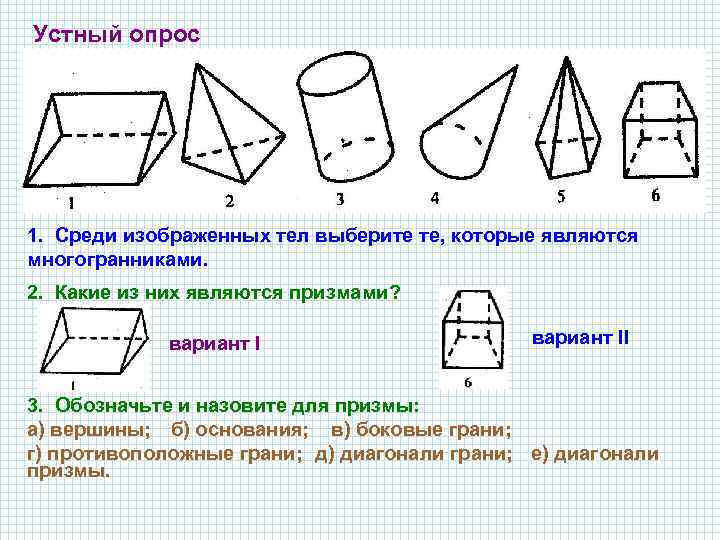Устный опрос 1. Среди изображенных тел выберите те, которые являются многогранниками. 2. Какие из них являются призмами? вариант II 3. Обозначьте и назовите для призмы: а) вершины; б) основания; в) боковые грани; г) противоположные грани; д) диагонали грани; е) диагонали призмы.

вариант I С С 1 В А вариант II В 1 А 1 а) вершины A, B, C, A 1, B 1, C 1; б) основания ABC, A 1 B 1 C 1; в) боковые грани ABB 1 A 1, ACC 1 A 1, BCC 1 B 1; г) противоположные грани ABC и A 1 B 1 C 1; д) диагонали граней АВ 1, А 1 В, АС 1, А 1 С, ВС 1, В 1 С; е) диагонали призмы - нет. С 1 D 1 А 1 В 1 С D А В а) вершины A, B, C, D, A 1, B 1, C 1, D 1; б) основания ABCD, A 1 B 1 C 1 D 1; в) боковые грани ABB 1 A 1, ACC 1 A 1, BDD 1 B 1, CDD 1 C 1; г) противоположные грани ABCD и A 1 B 1 C 1 D 1; ABB 1 A 1 и CDD 1 C 1; ACC 1 A 1 и BDD 1 B 1; д) диагонали граней АВ 1, А 1 В, АС 1, А 1 С, ВD 1, В 1 D, CD 1, DC 1, AD, BC, A 1 D 1, B 1 C 1; е) диагонали призмы – AD 1, DA 1, BC 1, CB 1.

4. Закончите предложения: 1) Высотой призмы называется … 2) Диагональю призмы называется … 3) Диагональным сечением призмы называется сечение плоскостью, проходящей через … 4) Параллелепипедом называется … 5) Кубом называется прямоугольный параллелепипед, у которого … 6) Примером моделей призмы и параллелепипеда из реальной жизни является …

5. Ответьте на вопросы: 1) Какие многоугольники лежат в основании призмы ? 2) В каких плоскостях лежат основания призмы? 3) Какими отрезками являются боковые ребра призмы? 4) Какими фигурами являются боковые грани призмы? 5) Что представляет диагональное сечение призмы? 6) Какими многоугольниками являются все грани параллелепипеда (любого)? 7) Какими фигурами являются все грани прямоугольного параллелепипеда? 8) Сколько измерений у прямоугольного параллелепипеда? 9) Почему все высоты призмы равны между собой? 10) Какие многоугольники являются основаниями и боковыми гранями пятиугольной призмы? 11) Сколько диагоналей в четырехугольной призме? 12) Призма имеет 30 граней. Какой многоугольник лежит в ее основании? Сколько вершин и ребер имеет эта призма?