Скачать презентацию 13 2010 W W Norton Company Скачать презентацию 13 2010 W W Norton Company

dd0f4f6d430dc0216ff63d90381b64ba.ppt

  • Количество слайдов: 55

13 © 2010 W. W. Norton & Company, Inc. Risky Assets 13 © 2010 W. W. Norton & Company, Inc. Risky Assets

Mean of a Distribution u. A random variable (r. v. ) w takes values Mean of a Distribution u. A random variable (r. v. ) w takes values w 1, …, w. S with probabilities 1, . . . , S ( 1 + · · · + S = 1). u The mean (expected value) of the distribution is the av. value of the r. v. ; © 2010 W. W. Norton & Company, Inc. 2

Variance of a Distribution u The distribution’s variance is the r. v. ’s av. Variance of a Distribution u The distribution’s variance is the r. v. ’s av. squared deviation from the mean; u Variance measures the r. v. ’s variation. © 2010 W. W. Norton & Company, Inc. 3

Standard Deviation of a Distribution u The distribution’s standard deviation is the square root Standard Deviation of a Distribution u The distribution’s standard deviation is the square root of its variance; u St. deviation also measures the r. v. ’s variability. © 2010 W. W. Norton & Company, Inc. 4

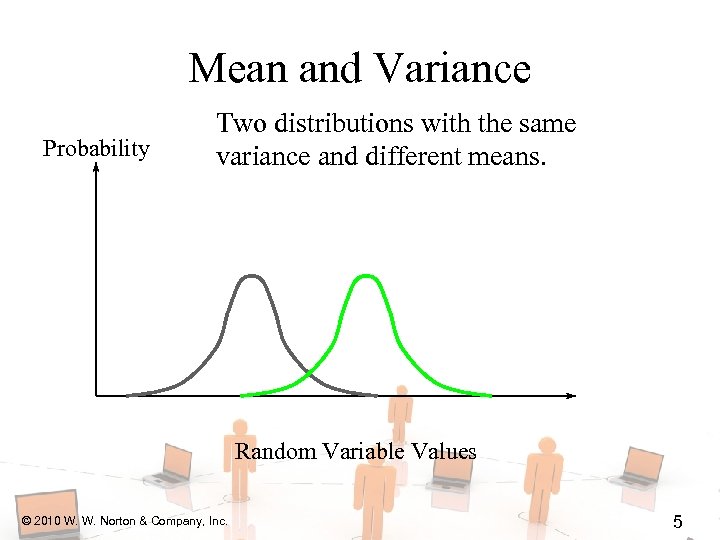Mean and Variance Probability Two distributions with the same variance and different means. Random Mean and Variance Probability Two distributions with the same variance and different means. Random Variable Values © 2010 W. W. Norton & Company, Inc. 5

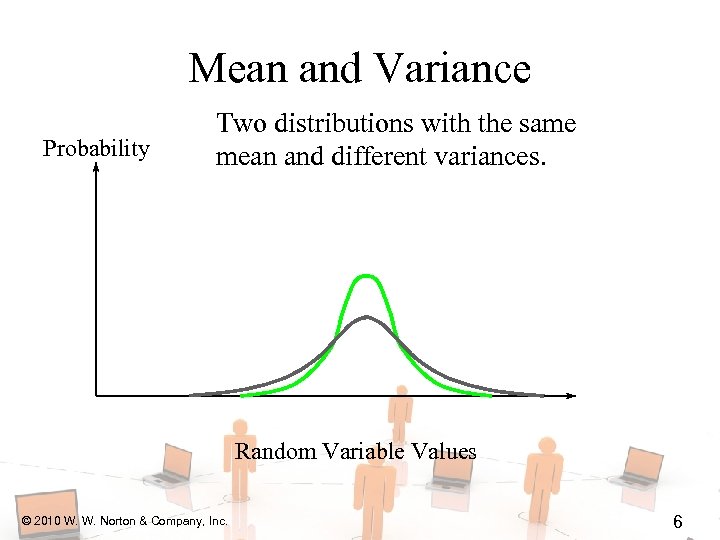Mean and Variance Probability Two distributions with the same mean and different variances. Random Mean and Variance Probability Two distributions with the same mean and different variances. Random Variable Values © 2010 W. W. Norton & Company, Inc. 6

Preferences over Risky Assets u Higher mean return is preferred. u Less variation in Preferences over Risky Assets u Higher mean return is preferred. u Less variation in return is preferred (less risk). © 2010 W. W. Norton & Company, Inc. 7

Preferences over Risky Assets u Higher mean return is preferred. u Less variation in Preferences over Risky Assets u Higher mean return is preferred. u Less variation in return is preferred (less risk). u Preferences are represented by a utility function U( , ). u U as mean return . u U as risk . © 2010 W. W. Norton & Company, Inc. 8

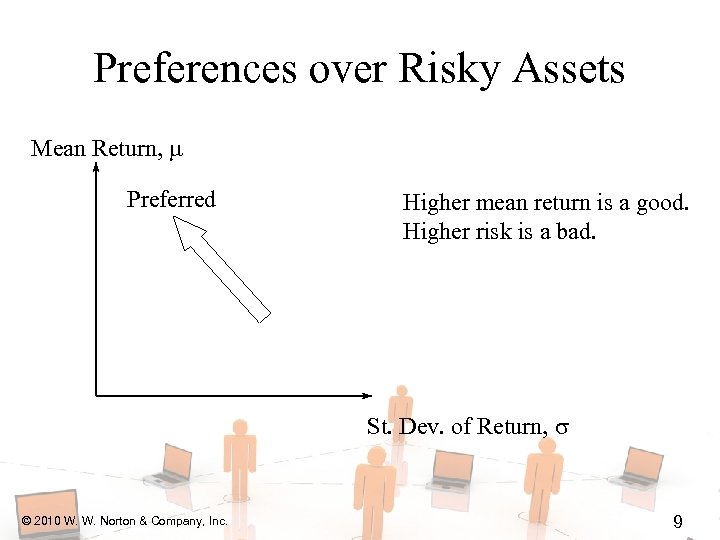Preferences over Risky Assets Mean Return, Preferred Higher mean return is a good. Higher Preferences over Risky Assets Mean Return, Preferred Higher mean return is a good. Higher risk is a bad. St. Dev. of Return, © 2010 W. W. Norton & Company, Inc. 9

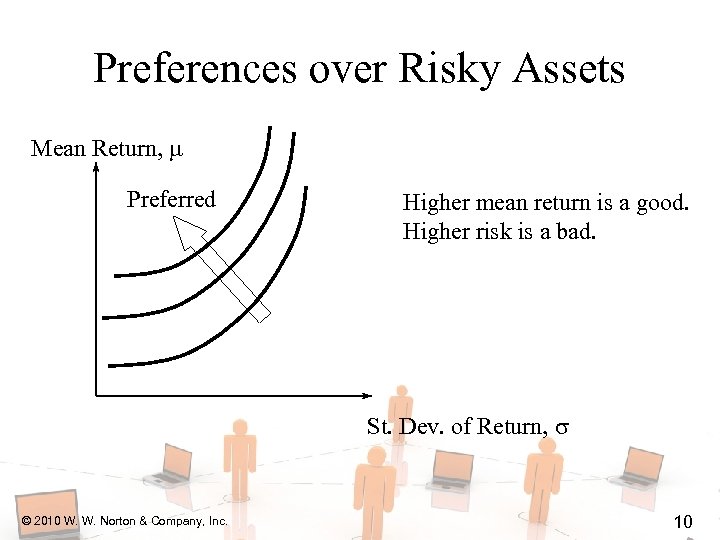Preferences over Risky Assets Mean Return, Preferred Higher mean return is a good. Higher Preferences over Risky Assets Mean Return, Preferred Higher mean return is a good. Higher risk is a bad. St. Dev. of Return, © 2010 W. W. Norton & Company, Inc. 10

Preferences over Risky Assets u How is the MRS computed? © 2010 W. W. Preferences over Risky Assets u How is the MRS computed? © 2010 W. W. Norton & Company, Inc. 11

Preferences over Risky Assets u How is the MRS computed? © 2010 W. W. Preferences over Risky Assets u How is the MRS computed? © 2010 W. W. Norton & Company, Inc. 12

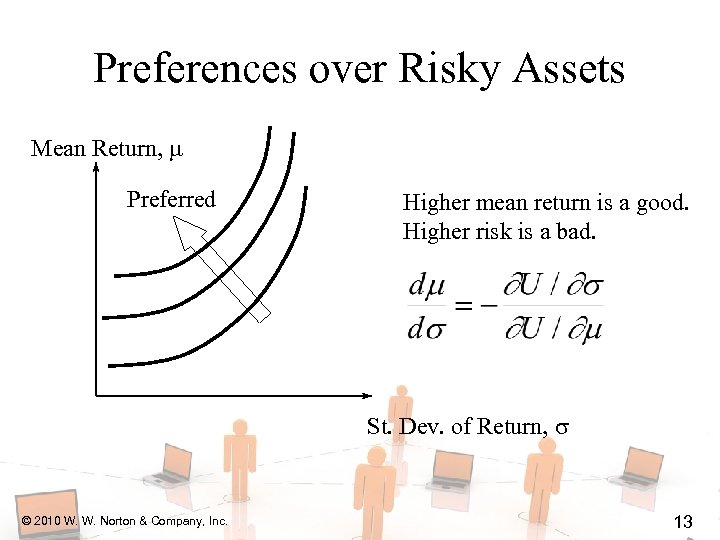Preferences over Risky Assets Mean Return, Preferred Higher mean return is a good. Higher Preferences over Risky Assets Mean Return, Preferred Higher mean return is a good. Higher risk is a bad. St. Dev. of Return, © 2010 W. W. Norton & Company, Inc. 13

Budget Constraints for Risky Assets u Two assets. u Risk-free asset’s rate-or-return is rf. Budget Constraints for Risky Assets u Two assets. u Risk-free asset’s rate-or-return is rf. u Risky stock’s rate-or-return is ms if state s occurs, with prob. s. u Risky stock’s mean rate-of-return is © 2010 W. W. Norton & Company, Inc. 14

Budget Constraints for Risky Assets u. A bundle containing some of the risky stock Budget Constraints for Risky Assets u. A bundle containing some of the risky stock and some of the risk-free asset is a portfolio. u x is the fraction of wealth used to buy the risky stock. u Given x, the portfolio’s av. rate-ofreturn is © 2010 W. W. Norton & Company, Inc. 15

Budget Constraints for Risky Assets x=0 © 2010 W. W. Norton & Company, Inc. Budget Constraints for Risky Assets x=0 © 2010 W. W. Norton & Company, Inc. and x = 1 16

Budget Constraints for Risky Assets x=0 and x = 1 Since stock is risky Budget Constraints for Risky Assets x=0 and x = 1 Since stock is risky and risk is a bad, for stock to be purchased must have © 2010 W. W. Norton & Company, Inc. 17

Budget Constraints for Risky Assets x=0 and x = 1 Since stock is risky Budget Constraints for Risky Assets x=0 and x = 1 Since stock is risky and risk is a bad, for stock to be purchased must have So portfolio’s expected rate-of-return rises with x (more stock in the portfolio). © 2010 W. W. Norton & Company, Inc. 18

Budget Constraints for Risky Assets u Portfolio’s © 2010 W. W. Norton & Company, Budget Constraints for Risky Assets u Portfolio’s © 2010 W. W. Norton & Company, Inc. rate-of-return variance is 19

Budget Constraints for Risky Assets u Portfolio’s © 2010 W. W. Norton & Company, Budget Constraints for Risky Assets u Portfolio’s © 2010 W. W. Norton & Company, Inc. rate-of-return variance is 20

Budget Constraints for Risky Assets u Portfolio’s © 2010 W. W. Norton & Company, Budget Constraints for Risky Assets u Portfolio’s © 2010 W. W. Norton & Company, Inc. rate-of-return variance is 21

Budget Constraints for Risky Assets u Portfolio’s © 2010 W. W. Norton & Company, Budget Constraints for Risky Assets u Portfolio’s © 2010 W. W. Norton & Company, Inc. rate-of-return variance is 22

Budget Constraints for Risky Assets u Portfolio’s © 2010 W. W. Norton & Company, Budget Constraints for Risky Assets u Portfolio’s © 2010 W. W. Norton & Company, Inc. rate-of-return variance is 23

Budget Constraints for Risky Assets u Portfolio’s © 2010 W. W. Norton & Company, Budget Constraints for Risky Assets u Portfolio’s © 2010 W. W. Norton & Company, Inc. rate-of-return variance is 24

Budget Constraints for Risky Assets Variance so st. deviation © 2010 W. W. Norton Budget Constraints for Risky Assets Variance so st. deviation © 2010 W. W. Norton & Company, Inc. 25

Budget Constraints for Risky Assets Variance so st. deviation x=0 © 2010 W. W. Budget Constraints for Risky Assets Variance so st. deviation x=0 © 2010 W. W. Norton & Company, Inc. and x = 1 26

Budget Constraints for Risky Assets Variance so st. deviation x=0 and x = 1 Budget Constraints for Risky Assets Variance so st. deviation x=0 and x = 1 So risk rises with x (more stock in the portfolio). © 2010 W. W. Norton & Company, Inc. 27

Budget Constraints for Risky Assets Mean Return, St. Dev. of Return, © 2010 W. Budget Constraints for Risky Assets Mean Return, St. Dev. of Return, © 2010 W. W. Norton & Company, Inc. 28

Budget Constraints for Risky Assets Mean Return, St. Dev. of Return, © 2010 W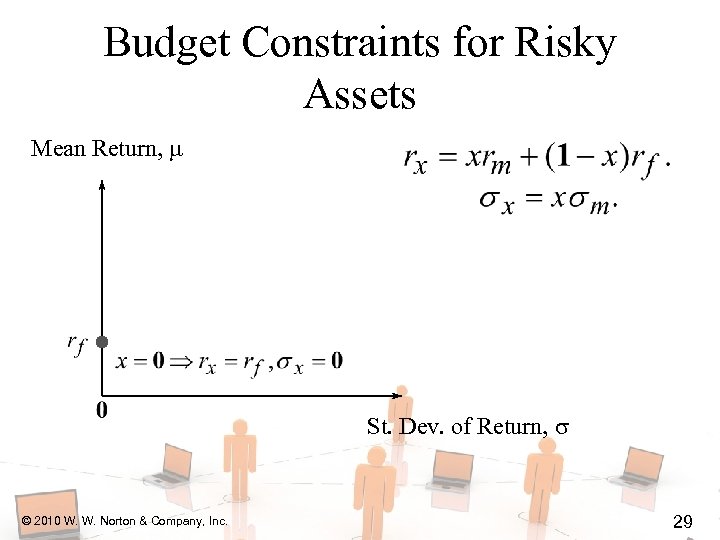. Budget Constraints for Risky Assets Mean Return, St. Dev. of Return, © 2010 W. W. Norton & Company, Inc. 29

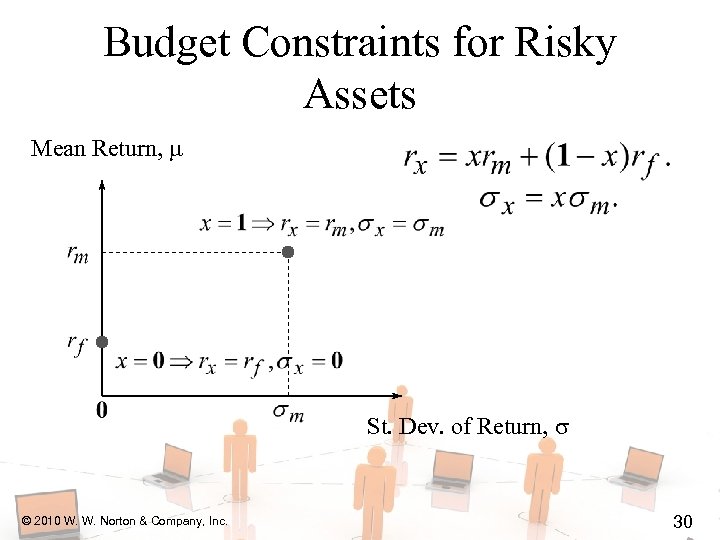Budget Constraints for Risky Assets Mean Return, St. Dev. of Return, © 2010 W. Budget Constraints for Risky Assets Mean Return, St. Dev. of Return, © 2010 W. W. Norton & Company, Inc. 30

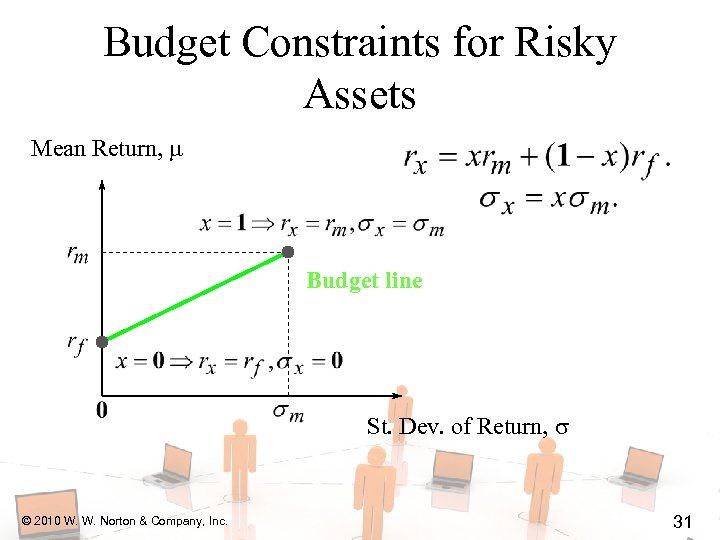Budget Constraints for Risky Assets Mean Return, Budget line St. Dev. of Return, © Budget Constraints for Risky Assets Mean Return, Budget line St. Dev. of Return, © 2010 W. W. Norton & Company, Inc. 31

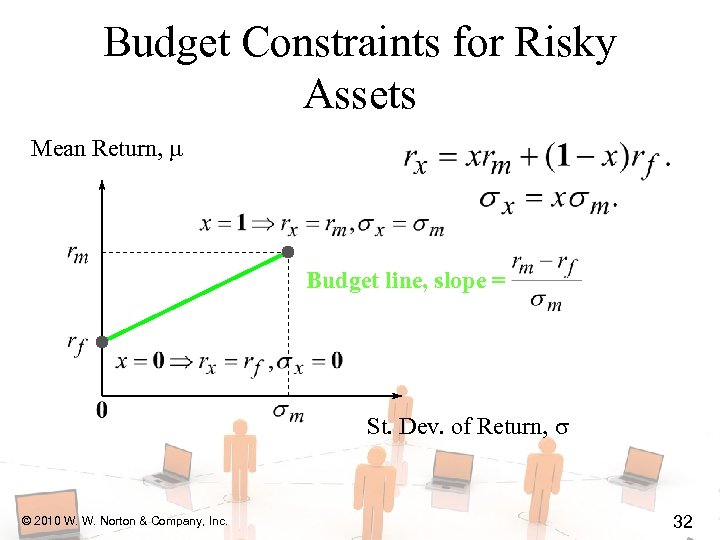Budget Constraints for Risky Assets Mean Return, Budget line, slope = St. Dev. of Budget Constraints for Risky Assets Mean Return, Budget line, slope = St. Dev. of Return, © 2010 W. W. Norton & Company, Inc. 32

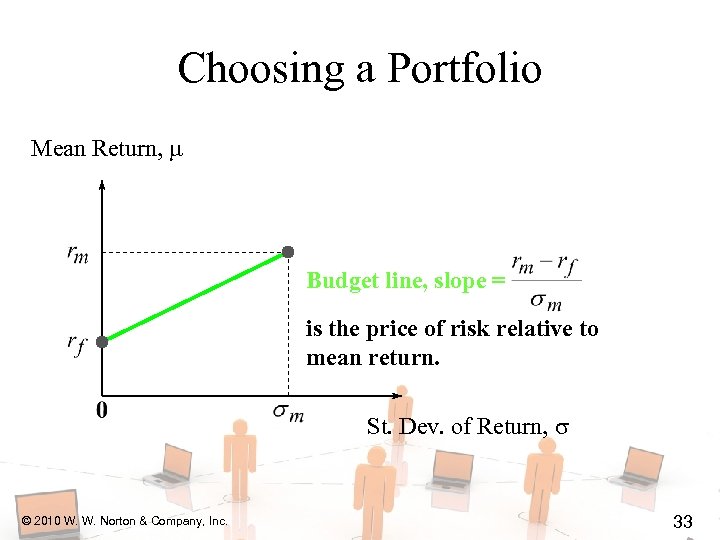Choosing a Portfolio Mean Return, Budget line, slope = is the price of risk Choosing a Portfolio Mean Return, Budget line, slope = is the price of risk relative to mean return. St. Dev. of Return, © 2010 W. W. Norton & Company, Inc. 33

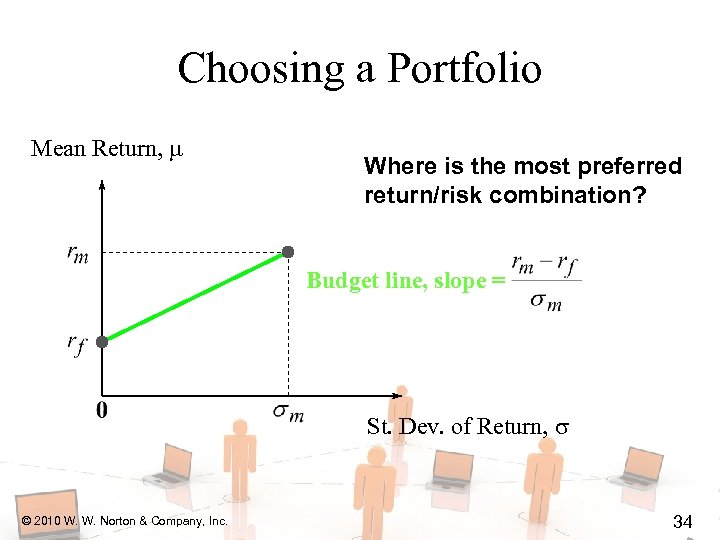Choosing a Portfolio Mean Return, Where is the most preferred return/risk combination? Budget line, Choosing a Portfolio Mean Return, Where is the most preferred return/risk combination? Budget line, slope = St. Dev. of Return, © 2010 W. W. Norton & Company, Inc. 34

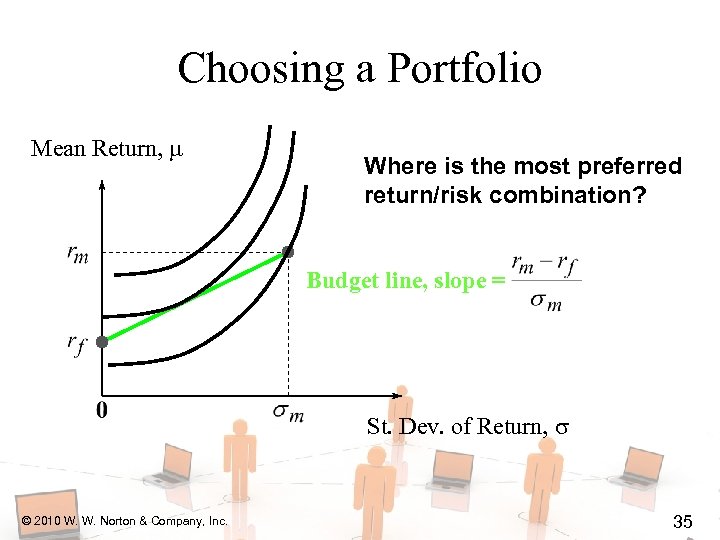Choosing a Portfolio Mean Return, Where is the most preferred return/risk combination? Budget line, Choosing a Portfolio Mean Return, Where is the most preferred return/risk combination? Budget line, slope = St. Dev. of Return, © 2010 W. W. Norton & Company, Inc. 35

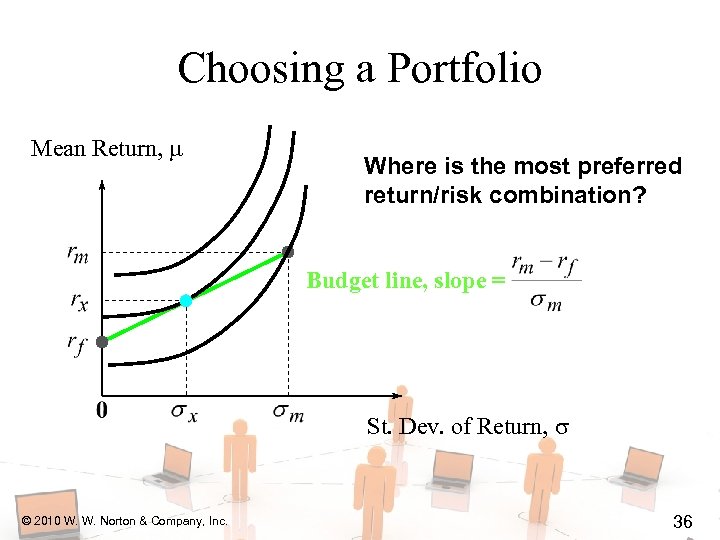Choosing a Portfolio Mean Return, Where is the most preferred return/risk combination? Budget line, Choosing a Portfolio Mean Return, Where is the most preferred return/risk combination? Budget line, slope = St. Dev. of Return, © 2010 W. W. Norton & Company, Inc. 36

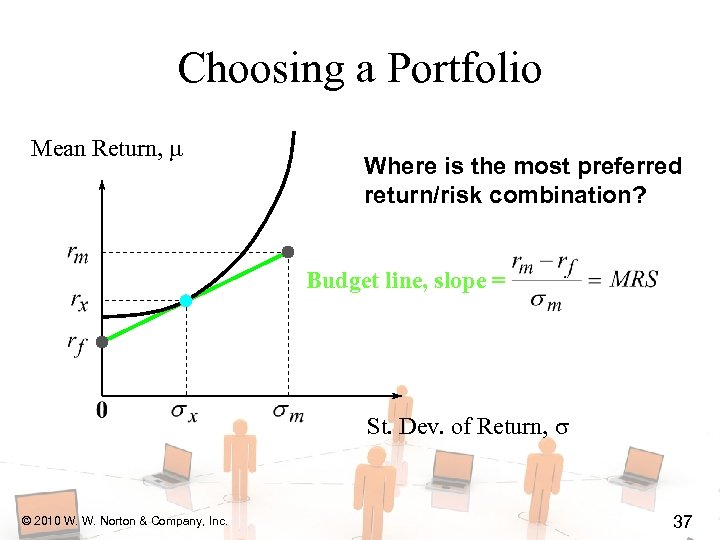Choosing a Portfolio Mean Return, Where is the most preferred return/risk combination? Budget line, Choosing a Portfolio Mean Return, Where is the most preferred return/risk combination? Budget line, slope = St. Dev. of Return, © 2010 W. W. Norton & Company, Inc. 37

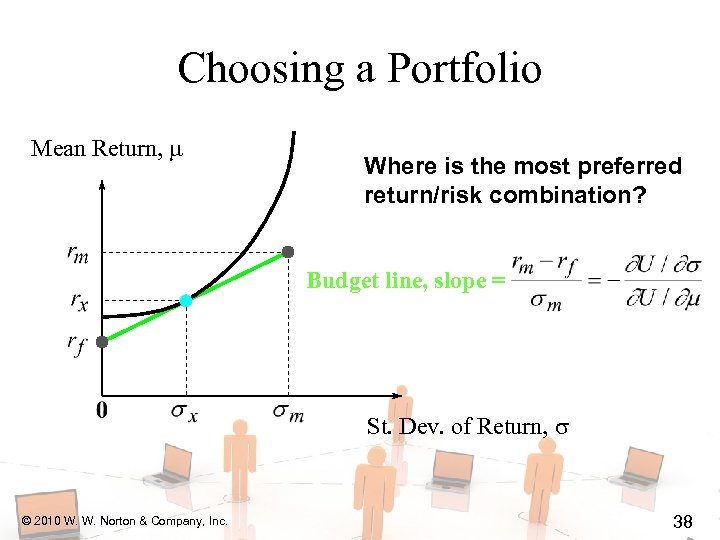Choosing a Portfolio Mean Return, Where is the most preferred return/risk combination? Budget line, Choosing a Portfolio Mean Return, Where is the most preferred return/risk combination? Budget line, slope = St. Dev. of Return, © 2010 W. W. Norton & Company, Inc. 38

Choosing a Portfolio u Suppose a new risky asset appears, with a mean rate-of-return Choosing a Portfolio u Suppose a new risky asset appears, with a mean rate-of-return ry > rm and a st. dev. y > m. u Which asset is preferred? © 2010 W. W. Norton & Company, Inc. 39

Choosing a Portfolio u Suppose a new risky asset appears, with a mean rate-of-return Choosing a Portfolio u Suppose a new risky asset appears, with a mean rate-of-return ry > rm and a st. dev. y > m. u Which asset is preferred? u Suppose © 2010 W. W. Norton & Company, Inc. 40

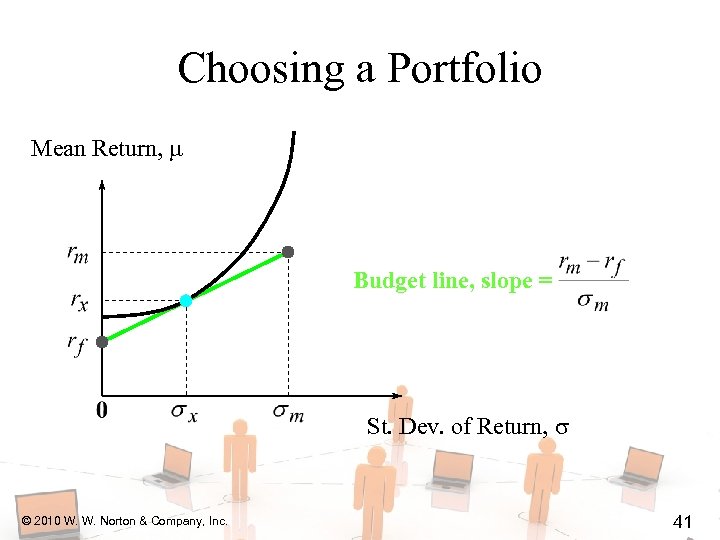Choosing a Portfolio Mean Return, Budget line, slope = St. Dev. of Return, © Choosing a Portfolio Mean Return, Budget line, slope = St. Dev. of Return, © 2010 W. W. Norton & Company, Inc. 41

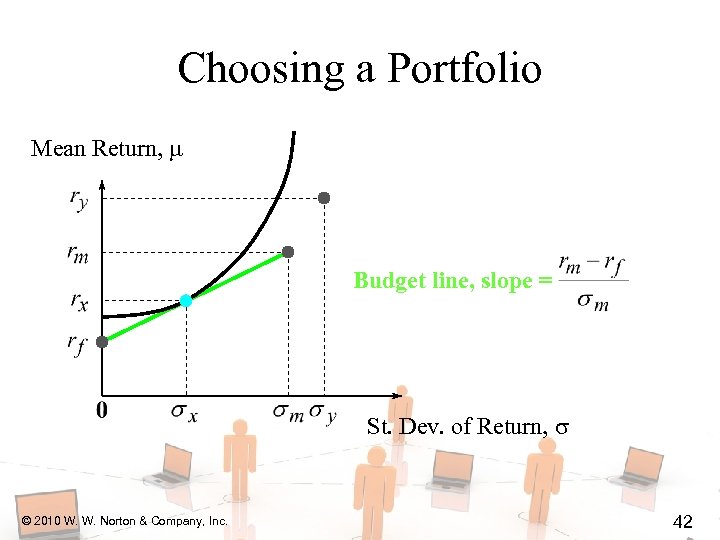Choosing a Portfolio Mean Return, Budget line, slope = St. Dev. of Return, © Choosing a Portfolio Mean Return, Budget line, slope = St. Dev. of Return, © 2010 W. W. Norton & Company, Inc. 42

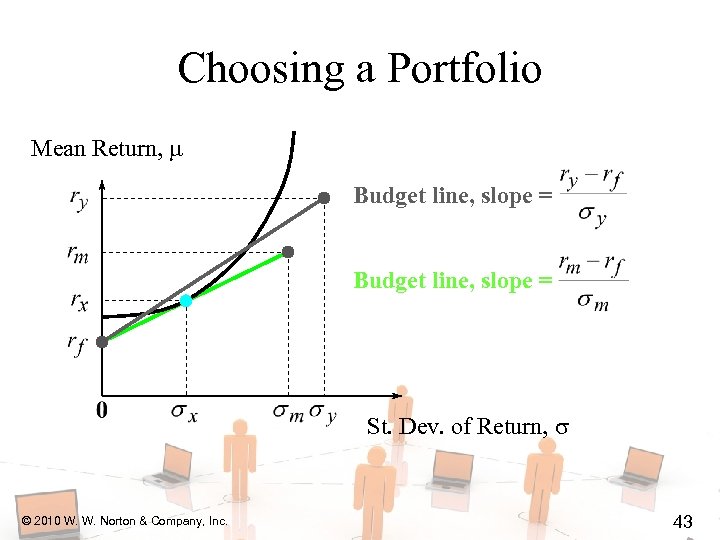Choosing a Portfolio Mean Return, Budget line, slope = St. Dev. of Return, © Choosing a Portfolio Mean Return, Budget line, slope = St. Dev. of Return, © 2010 W. W. Norton & Company, Inc. 43

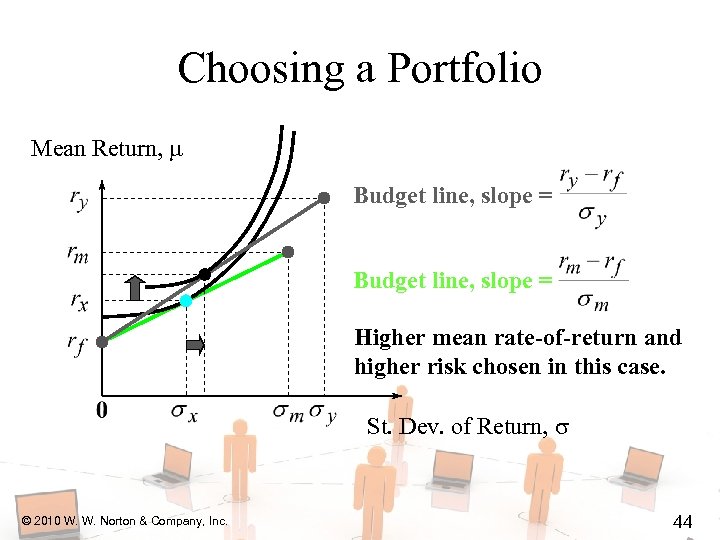Choosing a Portfolio Mean Return, Budget line, slope = Higher mean rate-of-return and higher Choosing a Portfolio Mean Return, Budget line, slope = Higher mean rate-of-return and higher risk chosen in this case. St. Dev. of Return, © 2010 W. W. Norton & Company, Inc. 44

Measuring Risk u Quantitatively, how risky is an asset? u Depends upon how the Measuring Risk u Quantitatively, how risky is an asset? u Depends upon how the asset’s value depends upon other assets’ values. u E. g. Asset A’s value is $60 with chance 1/4 and $20 with chance 3/4. u Pay at most $30 for asset A. © 2010 W. W. Norton & Company, Inc. 45

Measuring Risk u Asset A’s value is $60 with chance 1/4 and $20 with Measuring Risk u Asset A’s value is $60 with chance 1/4 and $20 with chance 3/4. u Asset B’s value is $20 when asset A’s value is $60 and is $60 when asset A’s value is $20 (perfect negative correlation of values). u Pay up to $40 > $30 for a 50 -50 mix of assets A and B. © 2010 W. W. Norton & Company, Inc. 46

Measuring Risk u Asset A’s risk relative to risk in the whole stock market Measuring Risk u Asset A’s risk relative to risk in the whole stock market is measured by © 2010 W. W. Norton & Company, Inc. 47

Measuring Risk u Asset A’s risk relative to risk in the whole stock market Measuring Risk u Asset A’s risk relative to risk in the whole stock market is measured by where is the market’s rate-of-return and is asset A’s rate-of-return. © 2010 W. W. Norton & Company, Inc. 48

Measuring Risk u asset A’s return is not perfectly correlated with the whole market’s Measuring Risk u asset A’s return is not perfectly correlated with the whole market’s return and so it can be used to build a lower risk portfolio. © 2010 W. W. Norton & Company, Inc. 49

Equilibrium in Risky Asset Markets u At equilibrium, all assets’ riskadjusted rates-of-return must be Equilibrium in Risky Asset Markets u At equilibrium, all assets’ riskadjusted rates-of-return must be equal. u How do we adjust for riskiness? © 2010 W. W. Norton & Company, Inc. 50

Equilibrium in Risky Asset Markets u Riskiness of asset A relative to total market Equilibrium in Risky Asset Markets u Riskiness of asset A relative to total market risk is A. u Total market risk is m. u So total riskiness of asset A is A m. © 2010 W. W. Norton & Company, Inc. 51

Equilibrium in Risky Asset Markets u Riskiness of asset A relative to total market Equilibrium in Risky Asset Markets u Riskiness of asset A relative to total market risk is A. u Total market risk is m. u So total riskiness of asset A is A m. u Price of risk is u So cost of asset A’s risk is p A m. © 2010 W. W. Norton & Company, Inc. 52

Equilibrium in Risky Asset Markets u Risk adjustment for asset A is u Risk Equilibrium in Risky Asset Markets u Risk adjustment for asset A is u Risk adjusted rate-of-return for asset A is © 2010 W. W. Norton & Company, Inc. 53

Equilibrium in Risky Asset Markets u At equilibrium, all risk adjusted rates -of-return for Equilibrium in Risky Asset Markets u At equilibrium, all risk adjusted rates -of-return for all assets are equal. u The risk-free asset’s = 0 so its adjusted rate-of-return is just u Hence, for every risky asset A. © 2010 W. W. Norton & Company, Inc. 54

Equilibrium in Risky Asset Markets u That at equilibrium in asset markets is the Equilibrium in Risky Asset Markets u That at equilibrium in asset markets is the main result of the Capital Asset Pricing Model (CAPM), a model used extensively to study financial markets. © 2010 W. W. Norton & Company, Inc. 55