12 Теория принятия решений 1 2 3 4

12. Теория принятия решений 1. 2. 3. 4. Основные понятия. Принятие решений в условиях полной определенности. Принятие решений в условиях риска. Принятие решений в условиях неопределенности.

1. Основные понятия При принятии управленческих решений о функционировании и развитии экономического объекта необходимо учитывать важную характеристику внешней среды – неопределенность. n Под неопределенностью следует понимать отсутствие, неполноту, недостаточность информации об объекте, процессе, явлении или неуверенность в достоверности информации. n Неопределенность обусловливает появление ситуаций, не имеющих однозначного исхода (решения). Среди различных видов ситуаций, с которыми в процессе производства сталкиваются предприятия, особое место занимают ситуации риска. n

Понятие риска Под ситуацией риска следует понимать сочетание, совокупность различных обстоятельств и условий, создающих обстановку того или иного вида деятельности. Ей сопутствуют три условия: наличие неопределенности; необходимость выбора альтернативы; возможность оценить вероятность осуществления выбираемых альтернатив. n Экономический риск применительно к процессам принятия решений в условиях неопределенности и риска, предстает в виде совокупности вероятных экономических, политических, нравственных и других положительных и неблагоприятных последствий, которые могут наступить при реализации выбранных решений. Риск оценивается вероятностью достижения желаемого результата, неудачи и отклонения от цели. n

Понятие риска В условиях риска доход сj от реализации единицы продукции j не является фиксированной величиной и это может быть случайной величиной, которая в общем случае описывается с помощью функции распределения f(cj). Часть дохода cjхj, определяемая продукцией j также случайная величина, если даже значение переменной xj определяющей уровень выпуска продукции j задан. В условиях неопределенности функция распределения f(cj) неизвестна. В действительности неопределенность не означает полного отсутствия информации о задаче. Например, известно, что cj может принимать пять значений, но неизвестны вероятности этих значений. Эта ситуация рассматривается как принятие решений в условиях неопределенности. Таким образом, с точки зрения полноты исходных данных определенность и неопределенность представляют два крайних случая, а риск определяет промежуточную ситуацию, в которой приходится принимать решение.

2. Принятие решений в условиях полной определенности Требуется определить оптимальное решение по обеспечению нового производства оборудованием. С помощью экспериментальных наблюдений были определены значения частных критериев функционирования соответствующего оборудования aij, выпускаемого тремя заводами изготовителями. n

Многокритериальная задача Очевидно, выбор оптимального варианта оборудования по одному критерию в данной задаче не вызывает затруднений. Например, если оценивать оборудование по надежности, то лучшим является оборудование завода 1 (решение х1). n Выбор оптимального решения по комплексу нескольких критериев (в нашем примере – по четырем критериям) является задачей многокритериальной. Один из подходов к решению многокритериальных задач управления связан с процедурой образования обобщенной функции Fi(ai 1, ai 2, …, ain), монотонно зависящей от критериев ai 1, ai 2, …, ain. Данная процедура называется процедурой (методом) свертывания критериев. Существует несколько методов свертывания, например: метод аддитивной оптимизации; метод многоцелевой оптимизации и др. n n

Метод аддитивной оптимизации n Аддитивный критерий оптимальности Величины λj являются весовыми коэффициентами, которые определяют в количественной форме степень предпочтения j-го критерия по сравнению с другими критериями. Другими словами, коэффициенты λj определяют важность j-го критерия оптимальности. n При этом более важному критерию приписывается больший вес, а общая важность всех критериев равна единице. n Применение: • частные критерии количественно соизмеримы по важности; • частные критерии являются однородными (имеют одинаковую размерность). n

Пример принятия решения при однородных частных критериях Необходимо выбрать оптимальный вариант оборудования по двум однородным локальным критериям: производительность (д. е. ); стоимость оборудования (д. е. ). На основе экспертных оценок были определены весовые коэффициенты этих двух частных критериев: λ 1 = 0, 667, λ 2 = 0, 333. n Очевидно, первый вариант оборудования по двум частным стоимостным критериям будет оптимальным, так как Fmax = F 1(a 1 j) = 5, 666. n

Схемы нормализации критериев § Под нормализацией критериев понимается такая последовательность процедур, с помощью которой все критерии приводятся к единому, безразмерному масштабу измерения. § Для этого определим максимум и минимум каждого локального критерия, т. е. § Выделим группу критериев αj, j=1, 2, …, ℓ, которые максимизируются при решении задачи, и группу критериев αj, j = ℓ, …, n, которые минимизируются при решении задачи. Тогда возможны следующие способы нормализации критериев

Пример принятия решения при неоднородных частных критериях Требуется определить оптимальную стратегию выбора оборудования из трех возможных (m = 3) с учетом четырех локальных критериев (n = 4). При этом предположим, что на основе экспертных оценок были определены веса частных критериев : λ 1 = 0, 4; λ 2 = 0, 2; λ 3 = 0, 1; λ 4 = 0, 3. 1. Определим максимум каждого локального критерия: a 1+ = 5, a 2+ = 7, a 3+ = 7, a 4+ = 6. 2. При решении задачи максимизируются первый (производительность) и четвертый (надежность) критерии, а минимизируются второй (стоимость оборудования) и третий (энергоемкость) критерии. 3. Исходя из принципа максимизации эффективности, нормализуем критерии: n

Нормализация критериев максимизации Нормализация критериев минимизации

Принятие решения 4. Определим обобщенную функцию цели по каждому варианту: n Оптимальным является первый вариант оборудования, так как Fmax = F 1 = 0, 729. n Рассмотренный подход к решению многокритериальных задач зачастую применяется при решении экономических задач, связанных с оценкой качества промышленной продукции и оценкой уровня технического совершенства технических n

3. Принятие решений в условиях риска Основными критериями оценки принимаемых решений в условиях риска являются: ожидаемое значение результата; ожидаемое значение результата в сочетании с минимизацией его дисперсии; известный предельный уровень результата; наиболее вероятное состояния. n Использование критерия ожидаемых значений предполагает возможность многократного решения одной и той же задачи, пока не будут получены достаточно точные расчётные формулы. n Математически это выглядит так: пусть Х – случайная величина с математическим ожиданием Mx и дисперсией Dx. Если x 1, x 2, . . . , xn – значения случайной величины X, то среднее арифметическое их значений хср = (х1+х2+…+хn)/n имеет дисперсию Dx/n. Таким образом, когда n , то Dx/n 0 и хср Mx. Другими словами при достаточно большом объёме выборки разница между средним арифметическим и математическим n

Применение критерия ожидаемых значений Предположим, что нужно вложить на фондовой бирже $ 10000 в акции одной из двух компаний: А или В. Акции компании А являются рискованными, но могут принести 50 % прибыли от суммы инвестиции на протяжении следующего года. Если условия фондовой биржи будут неблагоприятны (кодировки понижаются), сумма инвестиции может обесцениться на 20 %. n Компания В обеспечивает безопасность инвестиций с 15 % прибыли в условиях повышения котировок на бирже и только 5 % – в условиях понижения котировок. Все аналитические оценка показывают, что с вероятностью 0, 6 прогнозируют повышение котировок и с вероятностью 0, 4 – понижение котировок. Найти наиболее благоприятную компанию для вложения денежных средств. n

Описание альтеративных решений Дерево решений для задачи инвестирования А: 5000 * 0, 6 + (-2000) * 0, 4 = $ 2200. В: 1500 * 0, 6 + 500 * 0, 4 = $ 1100. В теории принятия решений повышение и понижение котировок на бирже именуются состояниями природы, возможные реализации которых являются случайными событиями (в данном случае с вероятностями 0, 6 и 0, 4).

Общая задача для критерия ожидаемых значений n. В общем случае задача принятия решений может включать n состояний природы и m альтернатив. Если pj – вероятность j-го состояния природы, а αij – платеж, связанный с принятием решения i при состоянии природы j (i = 1, 2, …, m; j = 1, 2, . . . , n), тогда ожидаемый платеж для решения i вычисляется в виде n. Mxi. = аi 1 р1, + аi 2 р2 +. . . + ain, pn, i = 1, 2, . . . , m, где р1 +р2 +. . . +рn = 1. n. Наилучшим решением будет то, которое соответствует Mxi* = maxi{Mxi} или Mxi* = mini{Mxi} в зависимости от того, является ли платеж в задаче доходом или убытком.

Критерий ожидаемого значения в сочетании с минимизацией его дисперсии Если необходимость в принятии решения встречается редко, то среднее выборочное значение может значительно отличаться от математического ожидания, а применение критерия ожидаемых значений может приводить к ошибочным результатам. В таких случаях рекомендуется применять критерий ожидаемого значения в сочетании с минимизацией его дисперсии, что приближает выборочное значение к математическому ожиданию. Критерий принимает следующий вид: n n n Mx + K*Dx min Mx - K*Dx max где К – заданная постоянная - определяет «степень важности» дисперсии Dx по отношению к Мx.

Критерий предельного уровня не позволяет получить оптимальное решение и дает возможность определить только приемлемый способ действий. n Например, транспортная фирма распродает автомобили, бывшие в эксплуатации. По каждой модели автомобиля определенного возраста определяется минимально допустимая цена продажи автомобиля на основании информации о распределении рыночных цен на подобные автомобили. Продажа автомобилей по цене ниже минимально допустимой приведет к убыточной работе транспортной фирмы. n Это и есть предельный уровень, позволяющий транспортной фирме согласиться на первое же превышающее этот уровень предложение цены. Такой критерий не определяет оптимальное решение, поскольку одно из последующих предложений может оказаться более выгодным, чем принятое. n

Критерий наиболее вероятного состояния Согласно критерию наиболее вероятного состояния, выбирается состояние природы, вероятность которого максимальна, и далее задача решается в условиях полной определенности в предположении, что обязательно будет иметь место выбранное состояние. Оптимальным считается действие, соответствующее максимальному значению полезности для выбранного состояния. n Следует отметить, что критерий наиболее вероятного состояния природы используется достаточно редко и в основном при существенном различии между максимальной вероятностью и остальными вероятностями состояний природы. n

4. Принятие решений в условиях неопределенности Пусть известны Si, i = 1, 2, …, n – возможные состояния природы, но неизвестно только, какое состояние будет иметь место, когда планируется реализация принимаемого управленческого решения. n Будем считать, что множество управленческих решений Rj также конечно и равно m. При этом реализация Rj управляющего решения в условиях, когда «природа» находится в Si состоянии, приводит к определенному результату, который можно оценить, введя количественную меру. В качестве этой меры могут служить выигрыши или потери от принимаемого решения. n

Матрица результатов Допустим, каждому Rj-му действию и каждому возможному Si-му состоянию «природы» соответствует определенный результат (выигрыш, полезность) при выборе j-го действия и реализации i-го состояния – Vji. n Следовательно, математическая модель задачи принятия решений определяется множеством состояний {Si}, множеством решений {Rj} и матрицей возможных результатов ||Vji||. В качестве результатов в отдельных задачах рассматривается матрица рисков ||rji||. n

Матица рисков Риск – это разность между результатом, который можно получить, если знать действительное состояние «природы» , и результатом, который будет получен при j-ом действии. Элементы матрицы рисков ||rji|| связаны с элементами матрицы полезностей (выигрышей) следующим соотношением: n rji = Vi - Vji, где Vi = maxj Vji – максимальный элемент в i-му столбце матрицы полезностей. n Если матрица возможных результатов ||Vji|| представляет собой матрицу потерь (затрат), то элементы матрицы рисков ||rji|| следует определять по формуле n rji = Vji - Vi, где Vi = minj Vji – минимальный элемент в i-му столбце матрицы потерь. n

Критерии принятия решений Непосредственный анализ матриц выигрышей ||Vji|| или рисков ||rji|| не позволяет в общем случае принять решение по выбору оптимального решения, за исключением тривиального случая, когда выигрыши при одном решении выше, чем при любом другом для каждого состояния «природы» (элементы матрицы выигрышей в некоторой строке больше, чем в любой из других). Другими словами, имеется в наличии «доминирующее» решение. n Для принятия решения в условиях неопределенности используется ряд критериев: Лапласа, Вальда, Сэвиджа, Гурвица и другие. n

Критерий Лапласа опирается на «принцип недостаточного основания» , согласно которому все состояния «природы» Si, i = 1, 2, …, n полагаются равновероятными. В соответствии с этим принципом каждому состоянию Si ставится вероятность q, определяемая по формуле q = 1/n. n Для принятия решения для каждого действия Rj вычисляют среднее арифметическое значение выигрыша: n n то есть находится действие Rj, соответствующее Для матрицы выигрышей Для матрицы рисков

Критерий Вальда (минимаксный или максиминный критерий) не требует знания вероятностей состояний Si. Этот критерий опирается на принцип наибольшей осторожности, поскольку он основывается на выборе наилучшего из наихудших решений Rj. n Если в исходной матрице результат Vji представляет потери лица, принимающего решение, то при выборе оптимального решения используется минимаксный критерий. Для определения оптимального решения Rj необходимо в каждой строке матрицы результатов найти наибольший элемент maxi {Vji}, а затем выбирается действие Rj (строка j), которому будет соответствовать наименьший элемент из этих наибольших элементов, т. е. действие, определяющее результат, равный W=minjmaxi{Vji} (для потерь) W=maхjmini{Vji} (для выигрышей) n Минимаксный критерий Вальда иногда приводит к нелогичным выводам из-за своей чрезмерной «пессимистичности» . n

Критерий Сэвиджа n Критерий Сэвиджа использует матрицу рисков ||rji||. Отметим, что независимо от того, является ли Vji доходом (выигрышем) или потерями (затратами), rji в обоих случаях определяет величину потерь лица, принимаюoего решение. Следовательно, можно применять к rji только минимаксный критерий. n Критерий Сэвиджа рекомендует в условиях неопределенности выбирать то решение Rj, при котором величина риска принимает наименьшее значение в самой неблагоприятной ситуации (когда риск максимален). n Применение критерия Сэвиджа позволяет любыми путями избежать большого риска при выборе решения, а значит, избежать большего проигрыша (потерь). n

Критерий Гурвица основан на следующих двух предположениях: «природа» может находиться в самом невыгодном состоянии с вероятностью (1 -α) и в самом выгодном состоянии с вероятностью α, здесь α – рассматривается как коэффициент доверия. Если результат Vji – прибыль, полезность, доход и т п. , то критерий Гурвица записывается так: n Когда Vji представляет затраты: n Если α = 0, то получим пессимистический критерий Вальда. Если α = 1, то приходим к решающему правилу вида maxjmахi. Vji или к так называемой стратегии «здорового оптимиста» , т. е. критерий слишком оптимистичный. n При отсутствии ярко выраженной склонности α = 0, 5 представляется наиболее разумной. n

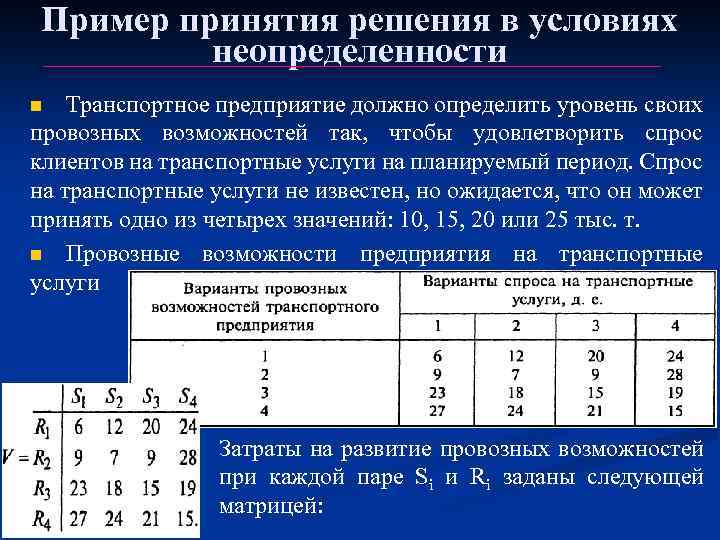Пример принятия решения в условиях неопределенности Транспортное предприятие должно определить уровень своих провозных возможностей так, чтобы удовлетворить спрос клиентов на транспортные услуги на планируемый период. Спрос на транспортные услуги не известен, но ожидается, что он может принять одно из четырех значений: 10, 15, 20 или 25 тыс. т. n Провозные возможности предприятия на транспортные услуги n Затраты на развитие провозных возможностей при каждой паре Si и Ri заданы следующей матрицей:

Применение критерия Лапласа Принцип Лапласа предполагает, что S 1, S 2, S 3, S 4 равновероятны. Следовательно, q = 1/4 = 0, 25 и ожидаемые затраты при различных действиях R 1, R 2, R 3, R 4 составляют: n Таким образом, наилучшим решением развития провозных возможностей в соответствии с критерием Лапласа будет R 2. n

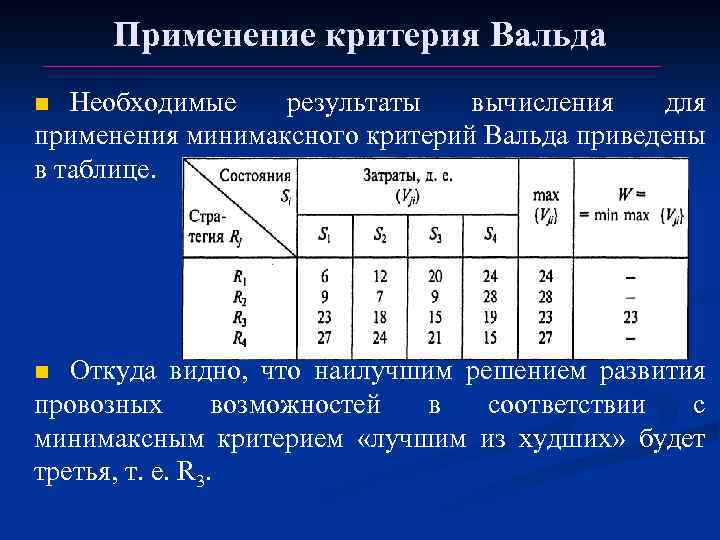Применение критерия Вальда Необходимые результаты вычисления для применения минимаксного критерий Вальда приведены в таблице. n Откуда видно, что наилучшим решением развития провозных возможностей в соответствии с минимаксным критерием «лучшим из худших» будет третья, т. е. R 3. n

Применение критерия Сэвиджа Для применения критерия Сэвиджа определяем матрицу рисков: n n и вычисляем величины риска для стратегий: Введение величины риска привело к выбору первой стратегии R 1, обеспечивающей наименьшие потери в самой неблагоприятной ситуации (когда риск максимален). n

Применение критерия Гурвица Результаты необходимых вычислений при (α = 0, 5) для критерия Гурвица представлены в следующей таблице n Таким образом, в примере предстоит сделать выбор: по критерию Лапласа – выбор стратегии R 2, по критерию Вальда – выбор стратегии R 3; по критерию Сэвиджа – выбор стратегии R 1; по критерию Гурвица – выбор стратегии R 1 при α = 0, 5. n

Выбор критерия принятия решений в условиях неопределенности является наиболее сложным и ответственным этапом в исследовании операций. При этом не существует какихлибо общих советов или рекомендаций. Выбор критерия должно производить лицо, принимающее решение, (ЛПР) с учетом конкретной специфики решаемой задачи и в соответствии со своими целями, а также опираясь на прошлый опыт и собственную интуицию. n В частности, если даже минимальный риск недопустим, то следует применять критерий Вальда. Если, наоборот, определенный риск вполне приемлем и ЛПР намерено вложить в некоторое предприятие столько средств, чтобы потом оно не сожалело, что вложено слишком мало, то выбирают критерий Сэвиджа. n