12 More about Equations 2 Case Study 12

12 More about Equations (2) Case Study 12. 1 Equations Reducible to Quadratic Equations 12. 2 Solving Simultaneous Equations 12. 3 Problems Leading to Quadratic Equations Chapter Summary 1

Case Study We have a budget of $40. Go and buy some yellow and red ribbons to decorate the classroom. I know that the yellow ribbon is $2 cheaper than the red ribbon. If we use all $40 to buy only one kind of ribbon, there will be one more roll of yellow ribbon than red ribbon and there will be no change. In order to find out the prices of a roll of yellow ribbon and a roll of red ribbon, we have to set up an equation. Let the prices of yellow ribbon and red ribbon be $x per roll and $(x 2) per roll respectively. According to the given conditions, Using the technique of solving quadratic equations, we can solve for x. 2

12. 1 Equations Reducible to Quadratic Equations In Book 4, we learnt how to solve quadratic equations. In fact, many equations are not quadratic in appearance, but they can be transformed into quadratic equations that can be solved easily. In this section, we will discuss four types of equations that can be transformed into quadratic equations: 1. 2. 3. 4. Fractional equations Higher degree equations Equations with surd form Indicial equations 3

12. 1 Equations Reducible to Quadratic Equations A. Fractional Equations Fractional equations are equations that consist of algebraic fraction in the form or . 4

12. 1 Equations Reducible to Quadratic Equations A. Fractional Equations Example 12. 1 T Solve . Solution: Expand the expression first. In this example, x cannot be zero. Do not forget to check whether the answers obtained can satisfy the given equation. Multiply both sides by x. 5

12. 1 Equations Reducible to Quadratic Equations A. Fractional Equations Example 12. 2 T Solve . Solution: If x 2 and x 6, we may multiply both sides by (x 2)(x 6). x 2 and x 6 6

12. 1 Equations Reducible to Quadratic Equations B. Higher Degree Equations Consider the equation 4 x 4 15 x 2 4 0. We can use the substitution y x 2 to transform the given equation into a quadratic equation 4 y 2 15 y 4 0. Then solve for y: 4 y 2 15 y 4 0 (4 y 1)(y 4) 0 y 4 or Since we are required to solve for the real roots of 4 x 4 15 x 2 4 0, substitute each of the values of y into y x 2: x 2 or 4 are not real numbers 7

12. 1 Equations Reducible to Quadratic Equations B. Higher Degree Equations Example 12. 3 T Find the real roots of the equation x 6 7 x 3 8 0. Solution: Let y x 3, the equation becomes y 1 or 8 Since y x 3, Do not stop here. We are required to find the values of x. The equation has 4 unreal roots which are the roots of the equations x 2 x 1 0 and x 2 2 x 4 0. 8

12. 1 Equations Reducible to Quadratic Equations C. Equations with Surd Form Consider the equation 2 x 6. We can use the substitution y to transform the given equation into a quadratic equation 2 y 2 y 6. 9

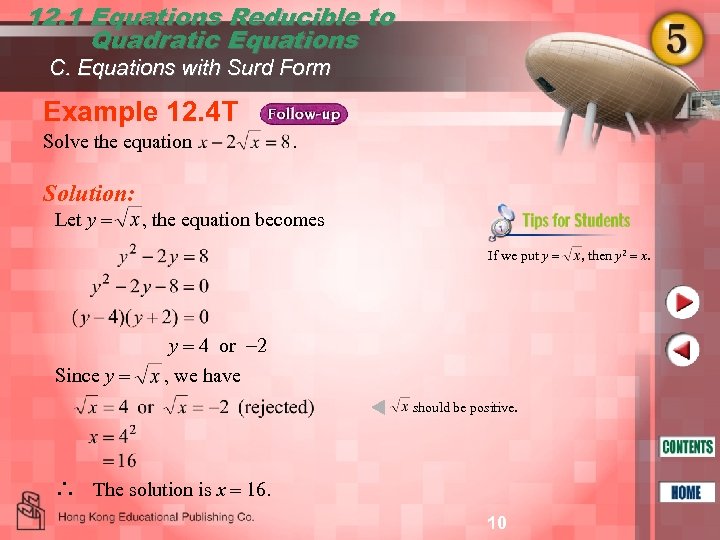
12. 1 Equations Reducible to Quadratic Equations C. Equations with Surd Form Example 12. 4 T Solve the equation . Solution: Let y , the equation becomes If we put y Since y y 4 or 2 , we have should be positive. ∴ The solution is x 16. 10 , then y 2 x.

12. 1 Equations Reducible to Quadratic Equations D. Indicial Equations 2 x x Consider the equation 3 3 12 0. It can be rewritten as (3 x)2 3 x 12 0. We can use the substitution y 3 x to transform the given equation into a quadratic equation y 2 y 12 0. Then solve for y: y 2 y 12 (y 3)(y 4) y x Since y 3 , 3 x 0 0 3 or 4 (rejected) 31 x 1 Since 3 x 0, for all real values of x, so 3 x 4 is rejected. 11

12. 1 Equations Reducible to Quadratic Equations D. Indicial Equations Example 12. 5 T Solve the equation 9 x 10(3 x) 24 0. (Give the answers correct to 3 significant figures. ) Solution: Rewrite the equation as (3 x)2 10(3 x) 24 0. Let y 3 x, the equation becomes y 4 or 6 Since y 3 x, we have: 3 x 4 or 3 x 6 log 3 x log 4 or log 3 x log 6 x log 3 log 4 or x log 3 log 6 or (cor. to 3 sig. fig. ) 12

12. 2 Solving Simultaneous Equations A. Solving Simultaneous Equations by the Algebraic Method In junior forms, we learnt how to solve a pair of simultaneous y 2 x 1 linear equations in two unknowns, such as . x 2 y 7 We can make one unknown (x or y) the subject of one of the linear equations, and then substitute the expression of that unknown into the other equation to eliminate that unknown. Finally, we can solve the linear equation in one unknown. For a pair of simultaneous equations in two unknowns in which one is y x 6 linear and the other is quadratic, such as , we can solve it 2 y x in a similar way. 13

12. 2 Solving Simultaneous Equations A. Solving Simultaneous Equations by the Algebraic Method To solve the simultaneous equations y y x 6 x 2 : Substituting (1) into (2), we have Substituting x 2 into (1), we have y 2 6 4. Substituting x 3 into (1), we have y 3 6 9. Notes: The solutions may also be written as ( 2, 4) or (3, 9). To find the value of the other unknown, we always substitute the known value into the linear equation. It is NOT appropriate to express the solutions as: x 2 or 3; y 4 or 9 14

12. 2 Solving Simultaneous Equations A. Solving Simultaneous Equations by the Algebraic Method Example 12. 6 T Solve x 2 x y y 3 x 6. Solution: The given equation can be expressed as: From (2), we have y 3 x 6. . . (3) Substituting (3) into (1), we have For the linear equation, we have to make y the subject first and then substitute it into the quadratic equation. x 2 or 6 Substituting x 2 into (3), we have y 3( 2) 6 0. Substituting x 6 into (3), we have y 3(6) 6 24. 15

12. 2 Solving Simultaneous Equations A. Solving Simultaneous Equations by the Algebraic Method Example 12. 7 T Consider the simultaneous equations: If the simultaneous equations do not have any real solutions, find the range of the values of k. Solution: Substituting (1) into (2), we have Since the simultaneous equations do not have any real solutions, the discriminant of (3) is D 0. 16

12. 2 Solving Simultaneous Equations A. Solving Simultaneous Equations by the Algebraic Method Example 12. 8 T Solve the simultaneous equations xy x 6 y 3. Solution: The given equation can be expressed as: From (2), we have x 3 6 y. . . (3) Substituting (3) into (1), we have Substituting y 1 into (3), x 3 6( 1) 3 Substituting y into (3), x 3 3 6 17

12. 2 Solving Simultaneous Equations B. Number of Points of Intersection of a Parabola and a Straight Line When solving a pair of simultaneous equations in which one is linear and the other is quadratic by the graphical method (which was discussed in Chapter 11), the graphs of the parabola and the straight line will satisfy one of the following situations: 1. Two distinct points 2. One point only 3. No points of intersection In actual practice, we can determine the number of points of intersection of the two graphs algebraically. 18

12. 2 Solving Simultaneous Equations B. Number of Points of Intersection of a Parabola and a Straight Line To determine the number of points of intersection of the two graphs algebraically: Step 1: Use the method of substitution to eliminate one of the variables (usually y) of the simultaneous equations. Then we get a quadratic equation in one variable. Step 2: Check the discriminant (D) of the quadratic equation obtained in Step 1. (a) If D 0, then there are two points of intersection. (b) If D 0, then there is only one point of intersection. (c) If D 0, then there are no points of intersection. 19

12. 2 Solving Simultaneous Equations B. Number of Points of Intersection of a Parabola and a Straight Line Example 12. 9 T Without solving the simultaneous equations, find the number of points of intersection of the parabola y x 2 5 x 6 and the line y x 4. Solution: Consider Substituting (2) into (1), The discriminant of (*) 62 4(1)( 10) 76 0 There are two points of intersection. 20

12. 2 Solving Simultaneous Equations B. Number of Points of Intersection of a Parabola and a Straight Line Example 12. 10 T If there are no points of intersection of the straight line y 2(x k) and the parabola y x 2 10 x 3, find the range of values of k. Solution: Consider the simultaneous equations Substituting (1) into (2), Since there are no points of intersection, the discriminant of equation (3) is D 0. 21

12. 3 Problems Leading to Quadratic Equations A. Practical Problems Involving Quadratic Equations In this section, we are going to solve problems involving equations which can be transformed into quadratic equations. Strategies for Solving Practical Problems Step 1: Study the problem carefully and understand the objective of the problem. Draw a figure or diagram if necessary. Step 2: First set a variable, say x, to one of the unknown quantities. Then try to represent all the other unknown quantities in terms of x. Step 3: Set up an equation that can be transformed into a quadratic equation. Step 4: Solve the equation. Step 5: Check all solutions in the context of the original problem. 22

12. 3 Problems Leading to Quadratic Equations A. Practical Problems Involving Quadratic Equations Example 12. 11 T In the figure, rectangle ABCD is similar to rectangle PQRS. Find the possible value(s) of x. Solution: Since ABCD is similar to PQRS, their corresponding sides are in proportion. 23

12. 3 Problems Leading to Quadratic Equations A. Practical Problems Involving Quadratic Equations Example 12. 12 T Eric cycles 18 km to a country park. On his return journey, he cycles 4 km/h faster. The total time taken for the whole journey is 99 minutes. (a) Find the speed of the return journey. (b) Find the time taken (in minutes) for the return journey. Solution: (a) Let x km/h be the speed of the return journey. Then the original speed is (x 4) km/h. Time taken for: the journey to the park the return journey hours The speed of the return journey is 24 km/h. 24

12. 3 Problems Leading to Quadratic Equations A. Practical Problems Involving Quadratic Equations Example 12. 12 T Eric cycles 18 km to a country park. On his return journey, he cycles 4 km/h faster. The total time taken for the whole journey is 99 minutes. (a) Find the speed of the return journey. (b) Find the time taken (in minutes) for the return journey. Solution: (b) Time taken for the return journey 25

12. 3 Problems Leading to Quadratic Equations A. Practical Problems Involving Quadratic Equations Example 12. 13 T Susan is going to make 70 teddy bears in N days. If she makes four more teddy bears each day, then she can take two days less to make 70 teddy bears. Find the value of N. Solution: Number of teddy bears that Susan originally makes each day New number of teddy bears that Susan makes each day New number of days taken N 2 26

12. 3 Problems Leading to Quadratic Equations B. Practical Problems Involving Simultaneous Equations We are now going to solve problems that lead to simultaneous equations in two unknowns. It is important to note that the solutions obtained must be checked since some solutions may not satisfy the problem. 27

12. 3 Problems Leading to Quadratic Equations B. Practical Problems Involving Simultaneous Equations Example 12. 14 T Consider a rectangle with dimensions x cm y cm. If the perimeter of the rectangle is 28 cm and the area is 49 cm 2, find x and y. Solution: Since the perimeter of the rectangle is 28 cm, we have Since the area of the rectangle is 49 cm 2, we have From (1), we have y 14 x. . . (3) Substituting (3) into (2), we have Substituting x 7 into (3), y 14 7 7 28

12. 3 Problems Leading to Quadratic Equations B. Practical Problems Involving Simultaneous Equations Example 12. 15 T A 18 cm long wire is cut into two parts for which each part is used to form a circle. If the sum of the areas bounded by the two circles is 53 cm 2, find the radii of the two circles. Solution: Let the radii of the 2 circles be x cm and y cm respectively, where x y. Since the sum of the circumferences of the 2 circles is 18 cm, we have 2 x 2 y 18 x y 9 y 9 x. . . (1) Since the sum of the areas of the 2 circles is 53 cm 2, we have x 2 y 2 53. . (2) Substituting (1) into (2), we have x 7 or 2 When x 7, y 2; When x 2, y 7. (rejected) The radii of the two circles are 7 cm and 2 cm. 29

Chapter Summary 12. 1 Equations Reducible to Quadratic Equations 1. 2. 3. 4. Fractional equations Higher degree equations Equations with surd form Indicial equations 30

Chapter Summary 12. 2 Solving Simultaneous Equations by the Algebraic Method 1. Use the method of substitution to solve a pair of simultaneous equations in two unknowns in which one is linear and the other is quadratic. 2. The number of points of intersection of a parabola and a line can be determined by the discriminant (D) of the quadratic equation in one of the unknowns (x or y). (a) If D 0, there are two points of intersection. (b) If D 0, there is one point of intersection. (c) If D 0, there are no points of intersection. 31

Chapter Summary 12. 3 Problems Leading to Quadratic Equations Strategies for solving practical problems: Step 1: Study and understand the problem. Step 2: Set a variable, say x, to one of the unknown quantities. Then try to represent all the other unknown quantities in terms of x. Step 3: Set up an equation that can be transformed into a quadratic equation. Step 4: Solve the equation. Step 5: Check all solutions in the context of the original problem. 32