12 General equilibrium An exchange economy Varian Chapter

12. General equilibrium: An exchange economy Varian, Chapter 30

The simplest market • Two people, or agents – Agent A and Agent B • Two goods – Good x and Good y • Agents interact by exchanging or trading goods • There is no production of either good

Questions we’re interested in • Will unregulated exchange lead to “good” outcomes? – Under what conditions? • How does trade occur? – Bargaining? – Using prices? • Can an outsider (e. g. , government) intervene to improve things?

Endowments (w. Ay+w. By) y • Endowments • Any possible bundle of goods for A is in this space A has (w. Ax, w. Ay) B has (w. Bx, w. By) Endowment w. Ay x Person A w. Ax (w. Ax+w. Bx)

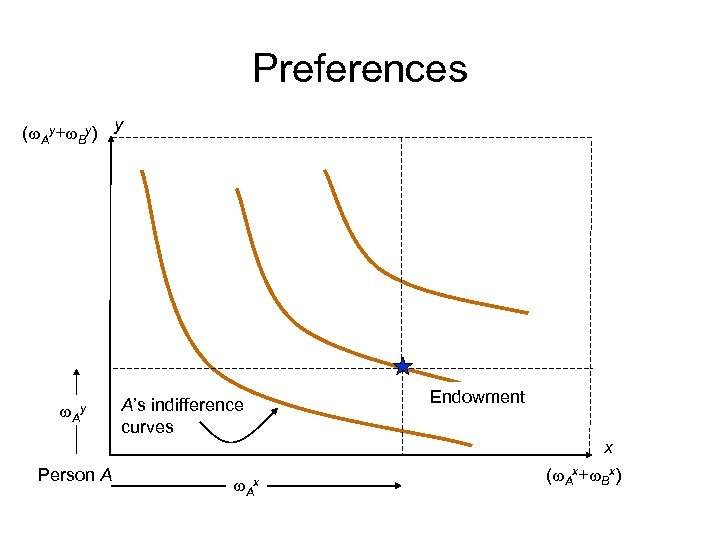
Preferences (w. Ay+w. By) y w. Ay A’s indifference curves Endowment x Person A w. Ax (w. Ax+w. Bx)

The simplest market • Allocation: A pair of consumption bundles – (x. A, y. A), (x. B, y. B) • Feasible allocation: pair of consumption bundles that add up to total endowment – (x. A, y. A)+(x. B, y. B)=(w. Ax, w. Ay)+(w. Bx, w. By)

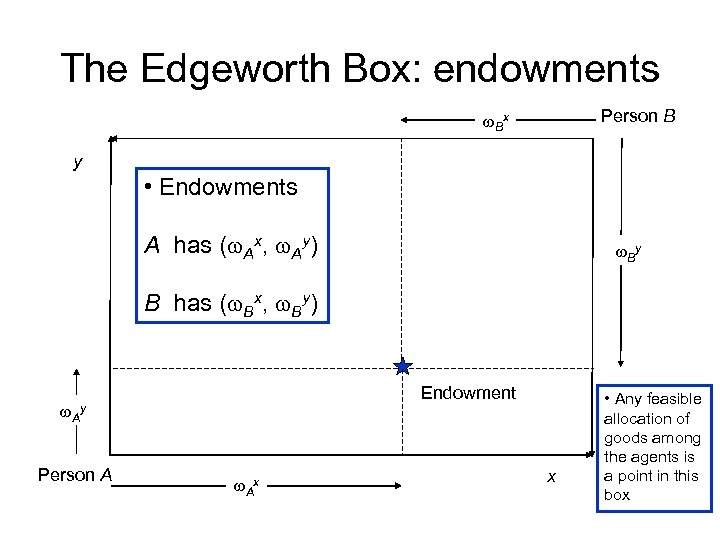
The Edgeworth Box: endowments Person B w. Bx y • Endowments A has (w. Ax, w. Ay) w. By B has (w. Bx, w. By) Endowment w. Ay Person A w. Ax x • Any feasible allocation of goods among the agents is a point in this box

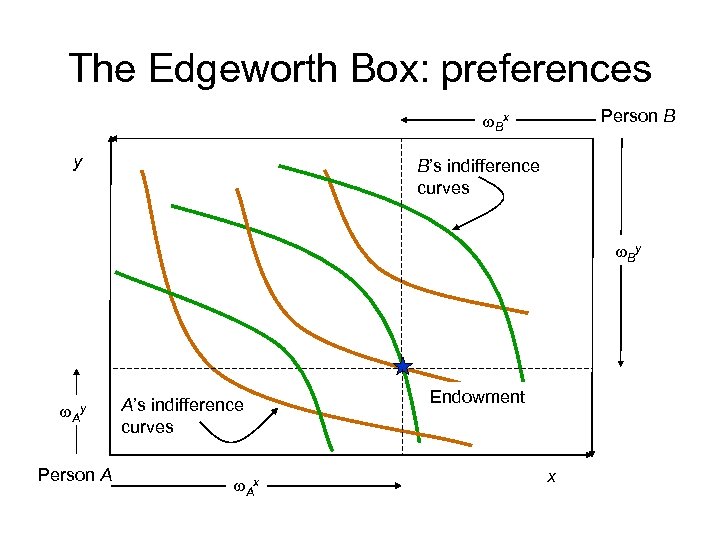
The Edgeworth Box: preferences Person B w. Bx y B’s indifference curves w. By w. Ay Person A A’s indifference curves w. Ax Endowment x

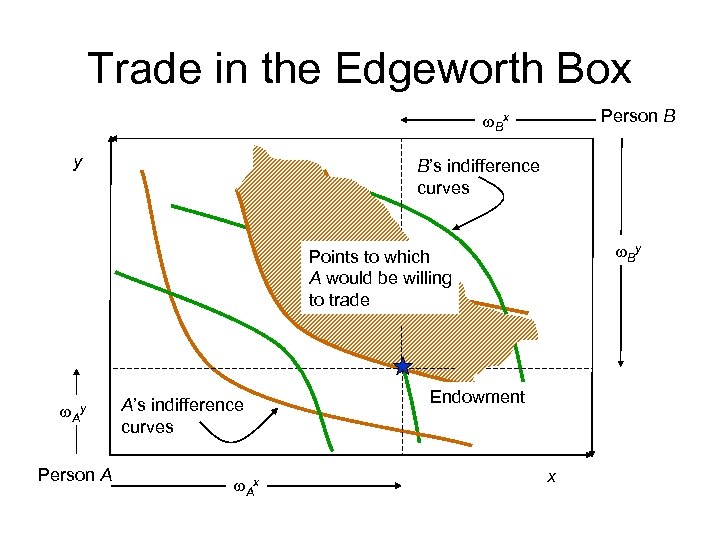
Trade in the Edgeworth Box Person B w. Bx y B’s indifference curves w. By Points to which A would be willing to trade w. Ay Person A A’s indifference curves w. Ax Endowment x

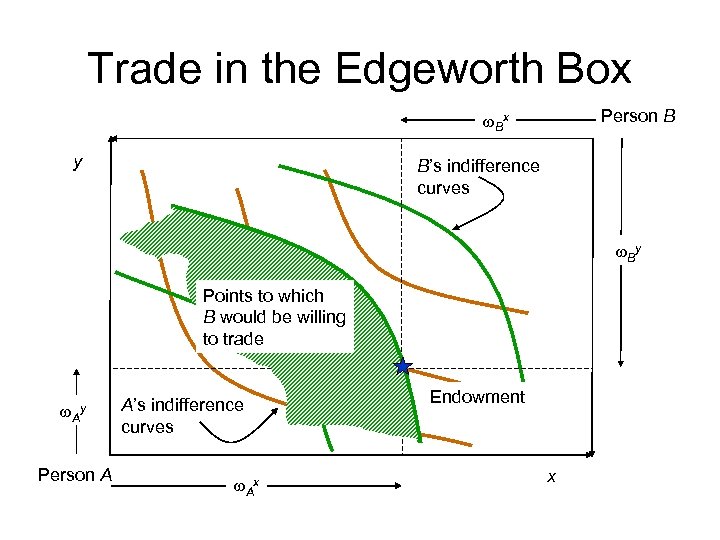
Trade in the Edgeworth Box Person B w. Bx y B’s indifference curves w. By Points to which B would be willing to trade w. Ay Person A A’s indifference curves w. Ax Endowment x

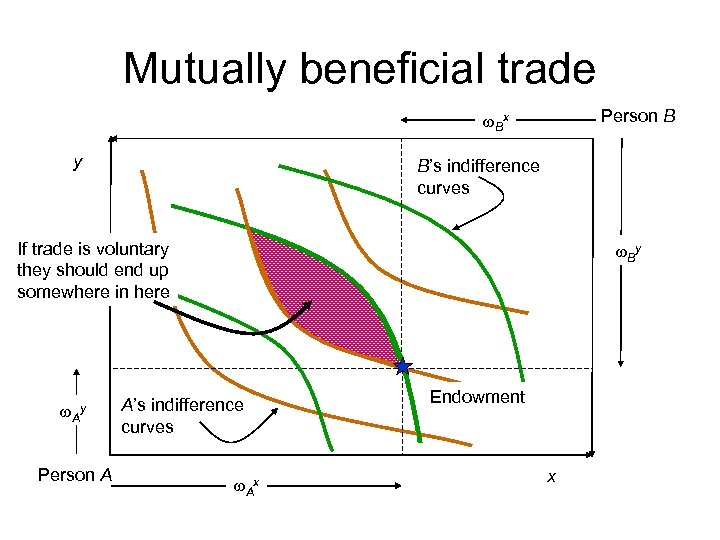
Mutually beneficial trade Person B w. Bx y B’s indifference curves If trade is voluntary they should end up somewhere in here w. Ay Person A w. By A’s indifference curves w. Ax Endowment x

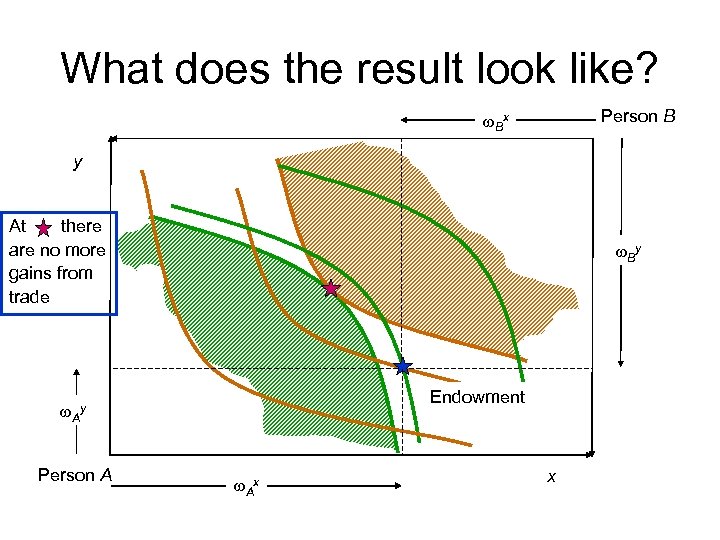
What does the result look like? Person B w. Bx y At there are no more gains from trade w. By Endowment w. Ay Person A w. Ax x

Describing potential outcomes • Pareto set, or contract curve: The set of all points that could be the outcome of a bargain – Depends on w – Can only make one individual better off by making the other worse off

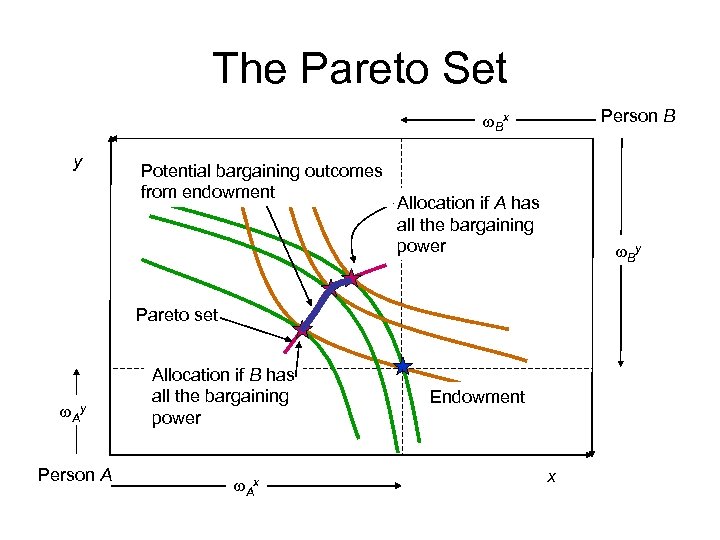
The Pareto Set Person B w. Bx y Potential bargaining outcomes from endowment Allocation if A has all the bargaining power w. By Pareto set w. Ay Person A Allocation if B has all the bargaining power w. Ax Endowment x

Example: Pareto set • Consumer A: – (w. Ax, w. Ay)=(5, 10) – u(x. A, y. A)=1/3 ln(x. A) + 2/3 ln(y. A) • Consumer B: – (w. Bx, w. By)=(10, 5) – u(x. B, y. B)=1/2 ln(x. B) + 1/2 ln(y. B) • Find the contract curve

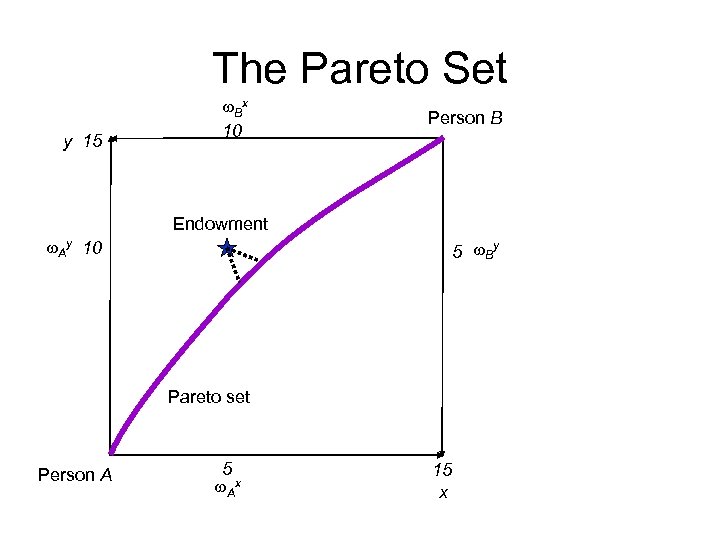
The Pareto Set y 15 w. Bx 10 Person B Endowment w. Ay 10 5 w. By Pareto set Person A 5 w. Ax 15 x

Can we narrow down outcomes? • So far we’ve said nothing about the mechanism or process by which people trade • We’ve found that agents should get to the contract curve…. . • …. . but we’re not sure what point they’ll reach on that curve • If trading is via prices, this indeterminacy can be resolved

What about prices? • A price-based process – – – Set py=1 Try a value of px=p Gives slope of budget line for both consumers Find gross demands of both consumers Vary p until demand is a feasible allocation • Excess supply of x – Lower p • Excess demand of x – Raise p

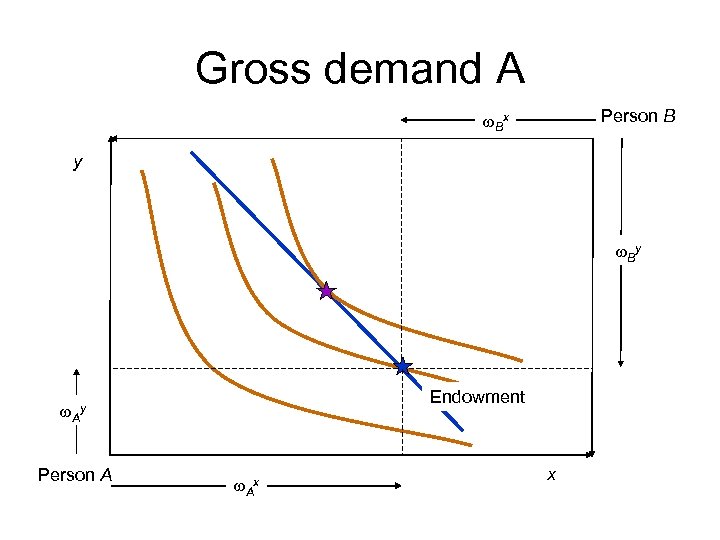
Gross demand A Person B w. Bx y w. By Endowment w. Ay Person A w. Ax x

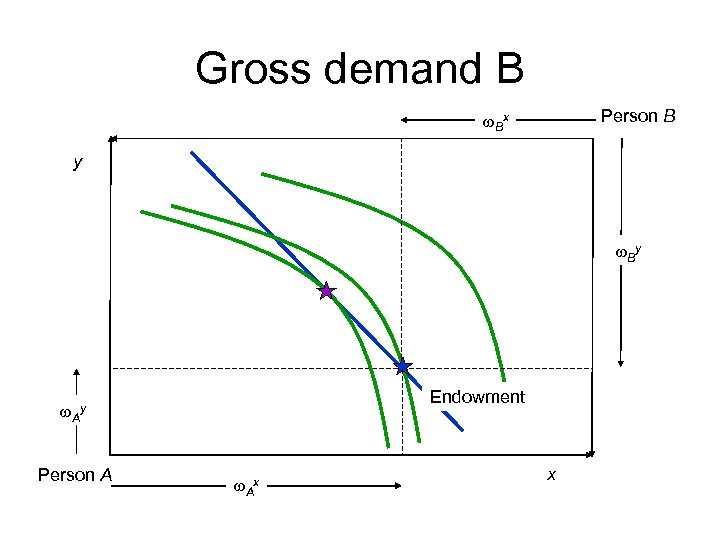
Gross demand B Person B w. Bx y w. By Endowment w. Ay Person A w. Ax x

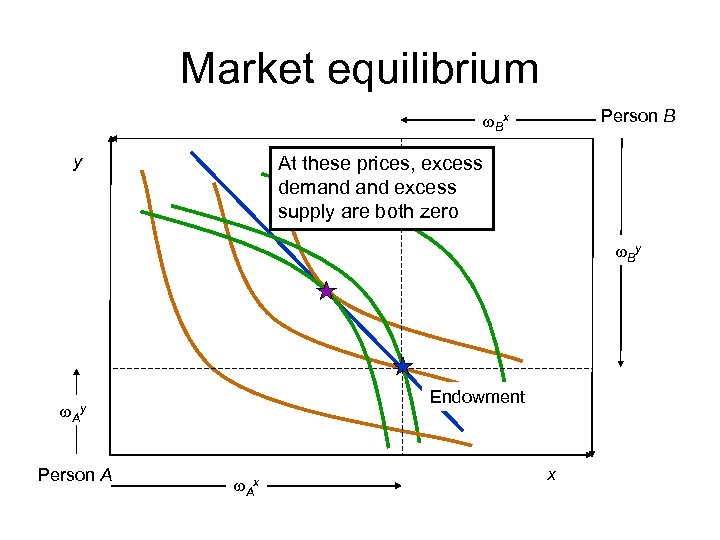
Market equilibrium Person B w. Bx y At these prices, excess demand excess supply are both zero w. By Endowment w. Ay Person A w. Ax x

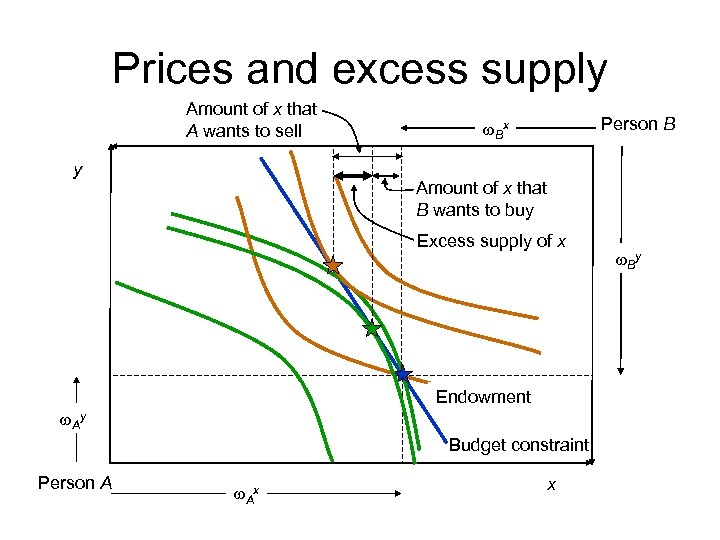
Prices and excess supply Amount of x that A wants to sell y Person B w. Bx Amount of x that B wants to buy Excess supply of x Endowment w. Ay Budget constraint Person A w. Ax x w. By

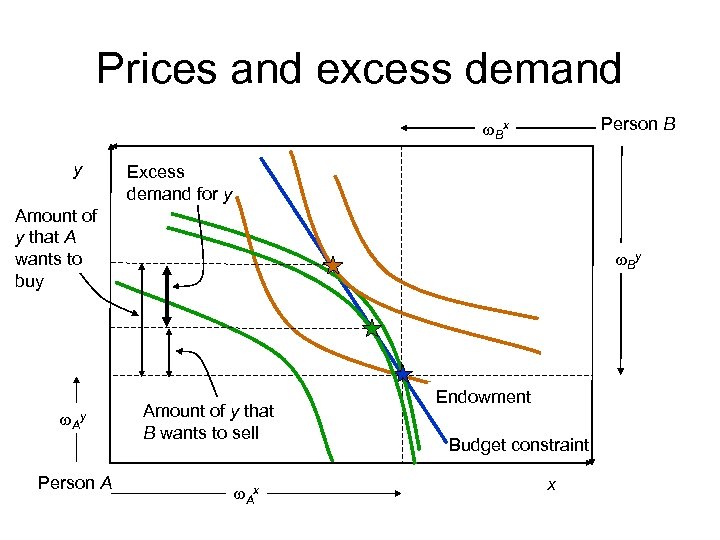
Prices and excess demand Person B w. Bx y Excess demand for y Amount of y that A wants to buy w. Ay Person A w. By Amount of y that B wants to sell w. Ax Endowment Budget constraint x

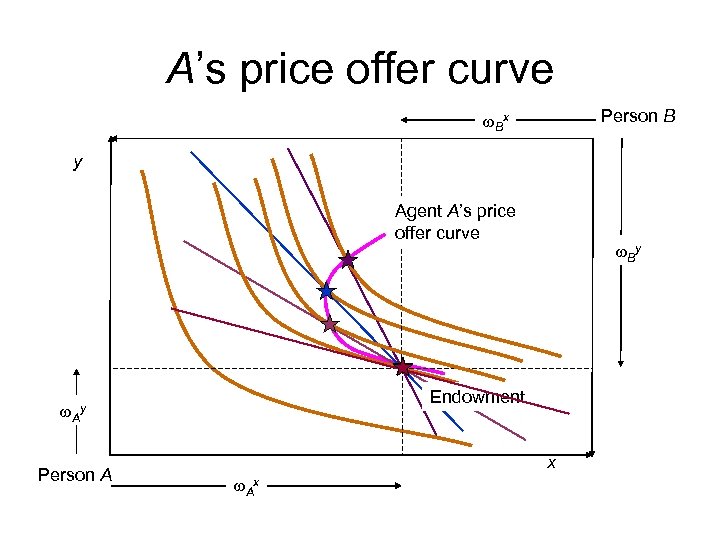
A’s price offer curve Person B w. Bx y Agent A’s price offer curve Endowment w. Ay Person A w. By x w. Ax

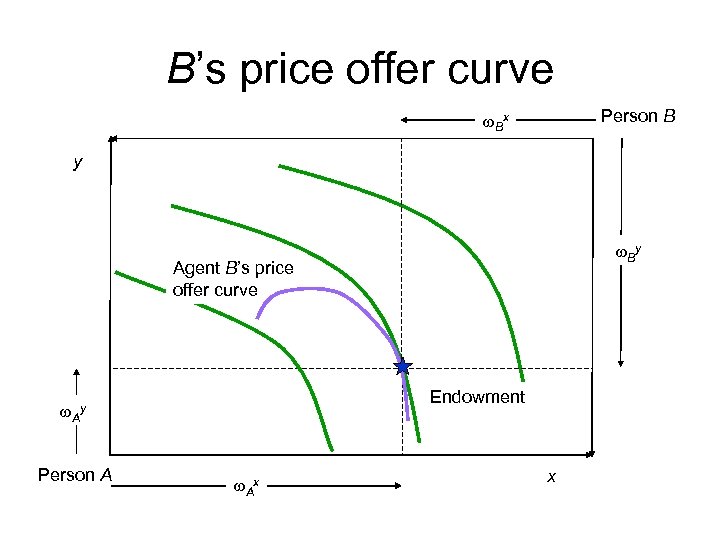
B’s price offer curve Person B w. Bx y w. By Agent B’s price offer curve Endowment w. Ay Person A w. Ax x

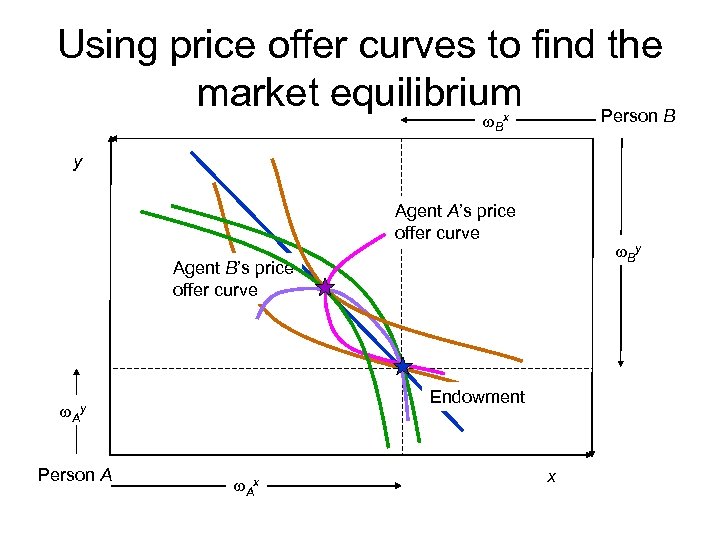
Using price offer curves to find the market equilibrium Person B w. Bx y Agent A’s price offer curve w. By Agent B’s price offer curve Endowment w. Ay Person A w. Ax x

Example: Price offer curves • Consumer A: – (w. Ax, w. Ay)=(5, 10) – u(x. A, y. A)=1/3 ln(x. A) + 2/3 ln(y. A) • Consumer B: – (w. Bx, w. By)=(10, 5) – u(x. B, y. B)=1/2 ln(x. B) + 1/2 ln(y. B) • Find the IOCs and the equilibrium allocation and price.

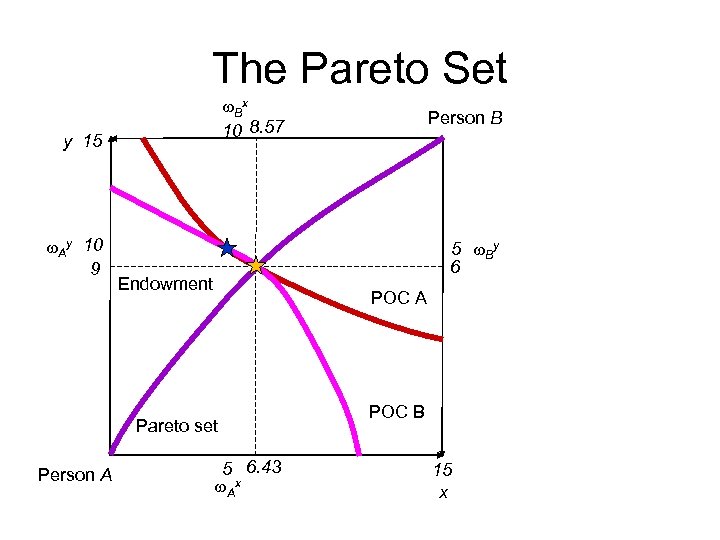
The Pareto Set w. Bx 10 8. 57 y 15 w. Ay 10 9 5 w. By 6 Endowment POC A Pareto set Person A Person B 5 6. 43 w. Ax POC B 15 x

The First Fundamental Theorem of Welfare Economics • The First Fundamental Theorem of Welfare Economics – All equilibria resulting from a competitive market are Pareto efficient – There are no gains from trade available from the result of a price-based exchange • There may be other undesirable properties of a market outcome

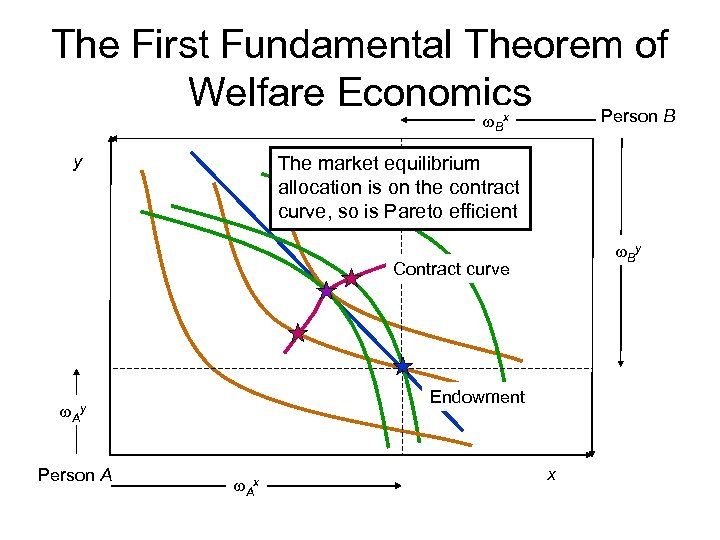
The First Fundamental Theorem of Welfare Economics Person B w. Bx y The market equilibrium allocation is on the contract curve, so is Pareto efficient w. By Contract curve Endowment w. Ay Person A w. Ax x

The Second Fundamental Theorem of Welfare Economics • The Second Fundamental Theorem of Welfare Economics – If preferences are convex, any Pareto efficient allocation can be reached by a competitive market, with the correct redistribution of the endowments – Using redistribution then allowing price-based trade, a planner can choose any PE allocation

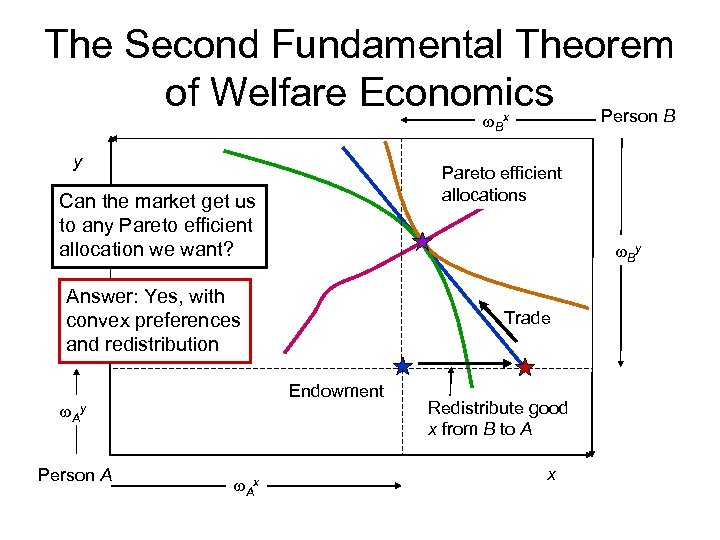
The Second Fundamental Theorem of Welfare Economics Person B w. Bx y Pareto efficient allocations Can the market get us to any Pareto efficient allocation we want? w. By Answer: Yes, with convex preferences and redistribution Endowment w. Ay Person A Trade w. Ax Redistribute good x from B to A x

Policy implications • How to help the poor – Give them money! – Price controls, quantity controls, etc lead to inefficient outcomes