12 ЭНЕРГЕТИЧЕСКИЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ 12 1

12. ЭНЕРГЕТИЧЕСКИЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ

12. 1. Потенциальная энергия деформации бруса В механике материалов широко используются понятия: напряжение, деформация, прочность, жесткость, т. е. по существу – понятия сил и перемещений. Более общим является подход к анализу работы материалов и конструкций под нагрузкой, основанный на анализе изменений потенциальной энергии. Энергетическая концепция лежит и в основе современной, быстро развивающейся науки – механики разрушения (как раздела механики деформируемого твердого тела). При нагружении упругого материала сила совершает работу на перемещении (при его деформации), т. е. в материале (при его нагружении - деформировании) накапливается потенциальная энергия деформации.

Потенциальной энергией деформации называется энергия, которая накапливается в теле при его упругом деформировании. Ранее нами уже рассматривалась методика определения потенциальной энергии при соответствующих ограничивающих условиях: – нагрузка прикладывается очень медленно, т. е. статически; – деформации материалов – упругие (действует закон Гука).

Запишем выражения для потенциальной энергии упругой деформации для простых видов нагружения. Растяжение (сжатие) N – продольная сила, Δℓ – абсолютная линейная деформация стержня, ℓ – длина участка стержня, F –площадь стержня, E – модуль Юнга.

Сдвиг Q – поперечная сила, Δs – абсолютный сдвиг, а – характерный размер сечения стержня, G – модуль сдвига. Кручение Mкр. – крутящий момент, φ – абсолютный угол закручивания, ℓ – длина участка стержня, Ip – полярный момент инерции сечения.

Чистый изгиб Мизг. – изгибающий момент, Θ – угол поворота сечения, ℓ – длина участка стержня, I – осевой момент инерции сечения. Все формулы имеют одинаковую структуру. В дальнейшем будем называть обобщенной силой P любую нагрузку (N, Q, Mкр. , Mизг. ), деформирующую конструкцию, и обобщенным перемещением Δ тот вид перемещения, на котором обобщенная сила производит работу (Δℓ, Δs, φ, θ).

Тогда любую из полученных формул можно записать в обобщенном виде: (12. 1) Потенциальная энергия деформации равна половине произведения обобщенной силы на обобщенное перемещение. В случае статического действия на упругую систему нескольких обобщенных сил P 1, P 2, … Pi, потенциальная энергия деформации определяется половиной суммы произведений каждой силы на значение соответствующего обобщенного перемещения (12. 2)

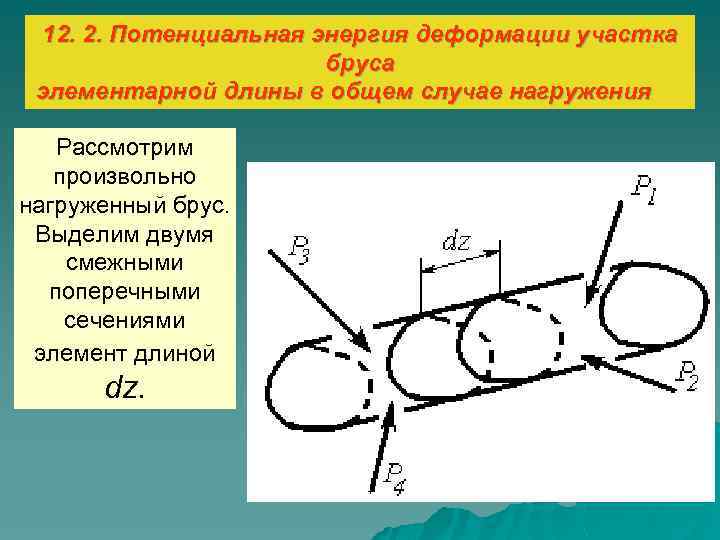12. 2. Потенциальная энергия деформации участка бруса элементарной длины в общем случае нагружения Рассмотрим произвольно нагруженный брус. Выделим двумя смежными поперечными сечениями элемент длиной dz.

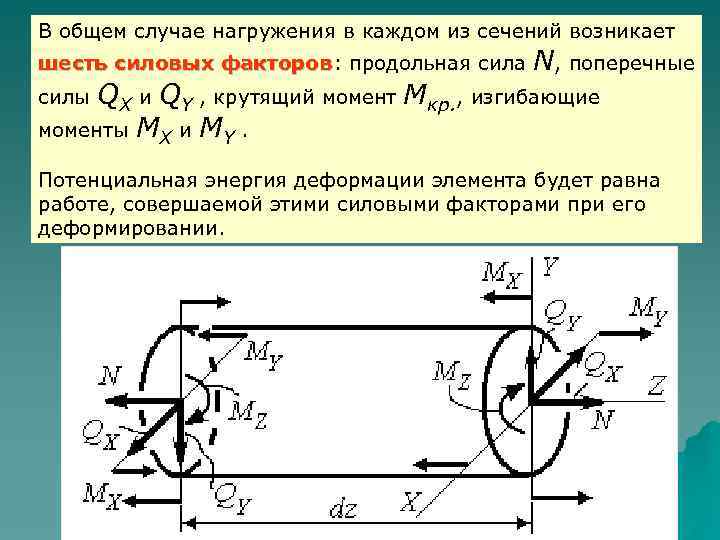В общем случае нагружения в каждом из сечений возникает шесть силовых факторов: продольная сила факторов N, поперечные QX и QY , крутящий момент Мкр. , изгибающие моменты MX и MY. силы Потенциальная энергия деформации элемента будет равна работе, совершаемой этими силовыми факторами при его деформировании.

Применим принцип независимости действия сил и определим потенциальную энергию для каждого из видов нагружения. Растяжение (сжатие) стержня элементарной длины dz и площадью F: Таким образом Полная энергия, накопленная при растяжении (сжатии) бруса длиной ℓ, состоящего из n участков (12. 3)

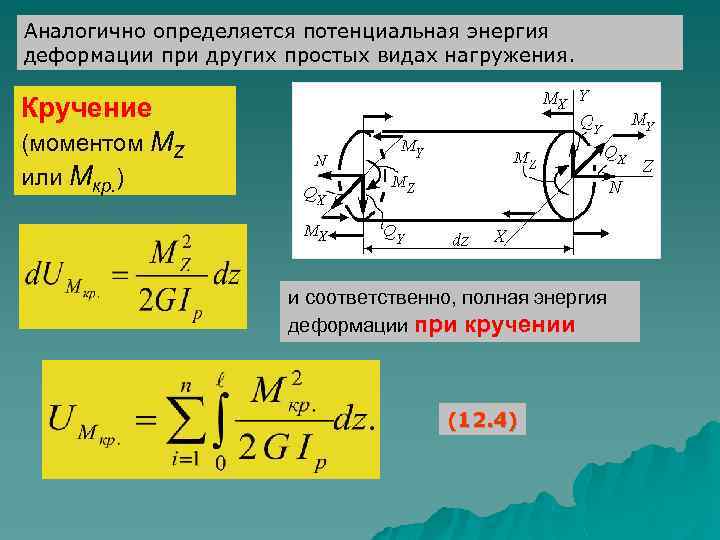Аналогично определяется потенциальная энергия деформации при других простых видах нагружения. Кручение (моментом МZ или Мкр. ) и соответственно, полная энергия деформации при кручении (12. 4)

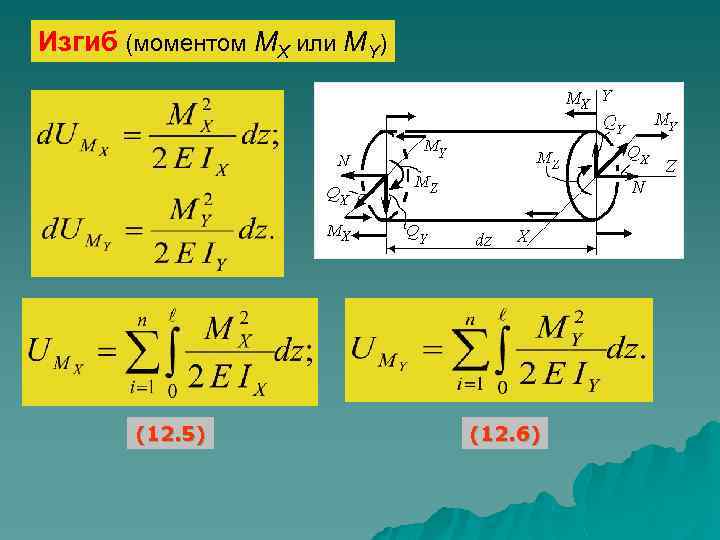Изгиб (моментом МX или МY) (12. 5) (12. 6)

Сдвиг от действия поперечных сил QX или QY Элементарная энергия определяется несколько сложнее, т. к. из теории поперечного изгиба помним, что касательные напряжения распределены неравномерно и описываются формулой Д. И. Журавского. В соответствии с законом Гука

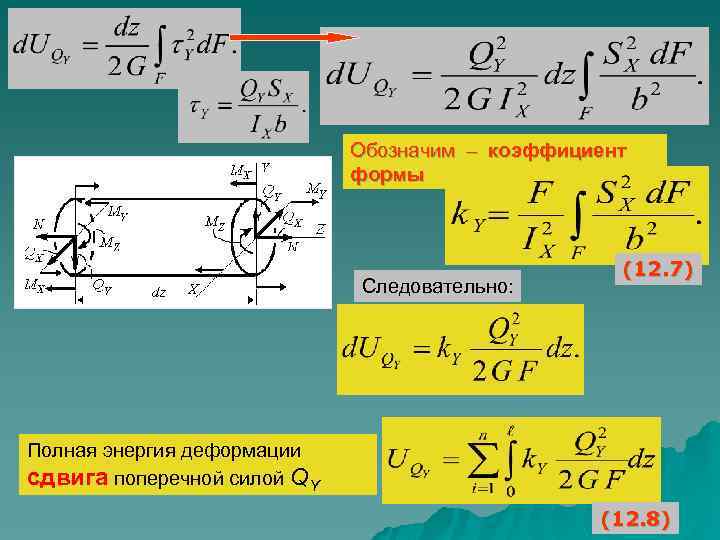Обозначим – коэффициент формы Следовательно: (12. 7) Полная энергия деформации сдвига поперечной силой QY (12. 8)

Аналогично, при сдвиге силой QX (12. 9) Величина коэффициентов k. X и k. Y зависит от формы поперечного сечения. Для прямоугольного сечения k. X = k. Y=1, 2; для круглого сечения k=1, 1; для прокатных профилей Fc – площадь стенки прокатного профиля.

В общем случае действия сил полная потенциальная энергия деформации бруса: (12. 10)

Пример. Определить потенциальную энергию деформации при плоском изгибе консольной стальной балки длиной ℓ прямоугольного сечения (со сторонами b и h), нагруженной равномерно распределенной нагрузкой В соответствии с (12. 10) интенсивностью q. При прямом поперечном изгибе в сечении балки действуют изгибающий момент и поперечная сила. В произвольном сечении балки:

Подставляем значения M и Q: Ответ:

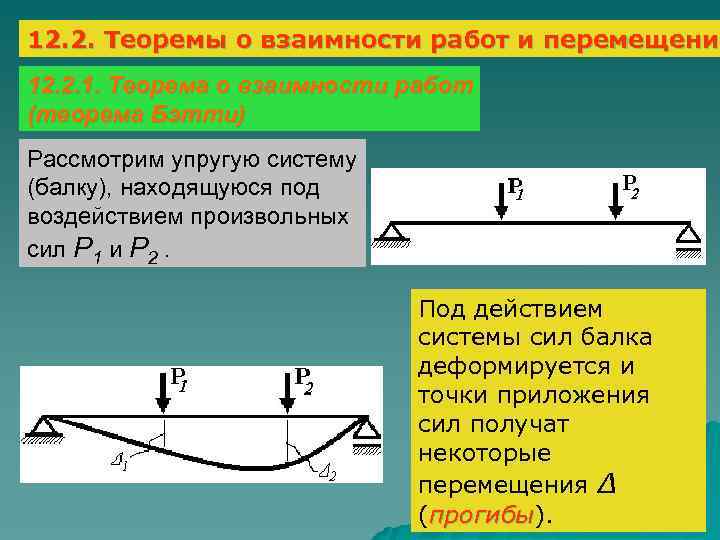12. 2. Теоремы о взаимности работ и перемещений перемещени 12. 2. 1. Теорема о взаимности работ (теорема Бэтти) Рассмотрим упругую систему (балку), находящуюся под воздействием произвольных сил P 1 и P 2. Под действием системы сил балка деформируется и точки приложения сил получат некоторые перемещения Δ (прогибы). прогибы

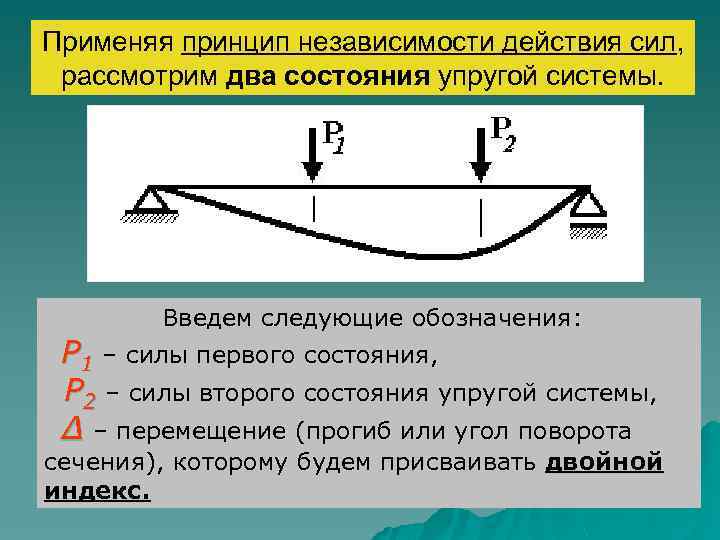Применяя принцип независимости действия сил, рассмотрим два состояния упругой системы. Введем следующие обозначения: Р 1 – силы первого состояния, Р 2 – силы второго состояния упругой системы, Δ – перемещение (прогиб или угол поворота сечения), которому будем присваивать двойной индекс.

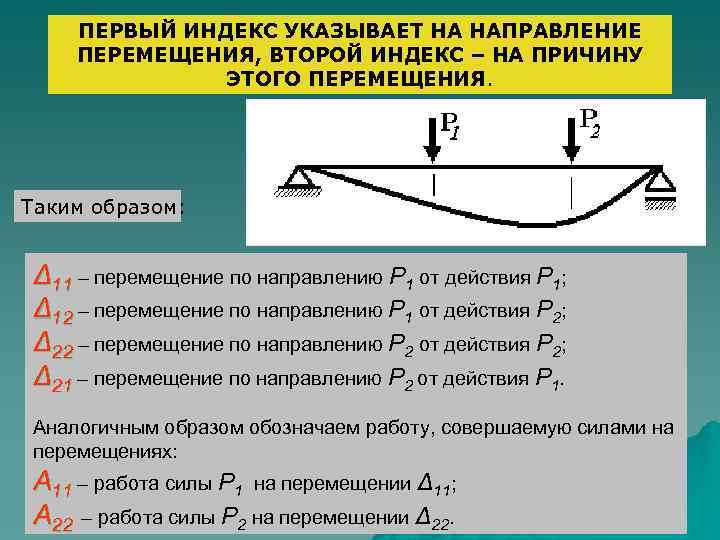ПЕРВЫЙ ИНДЕКС УКАЗЫВАЕТ НА НАПРАВЛЕНИЕ ПЕРЕМЕЩЕНИЯ, ВТОРОЙ ИНДЕКС – НА ПРИЧИНУ ЭТОГО ПЕРЕМЕЩЕНИЯ. Таким образом: Δ 11 – перемещение по направлению Р 1 от действия Р 1; Δ 12 – перемещение по направлению Р 1 от действия Р 2; Δ 22 – перемещение по направлению Р 2 от действия Р 2; Δ 21 – перемещение по направлению Р 2 от действия Р 1. Аналогичным образом обозначаем работу, совершаемую силами на перемещениях: A 11 – работа силы Р 1 на перемещении Δ 11; A 22 – работа силы Р 2 на перемещении Δ 22.

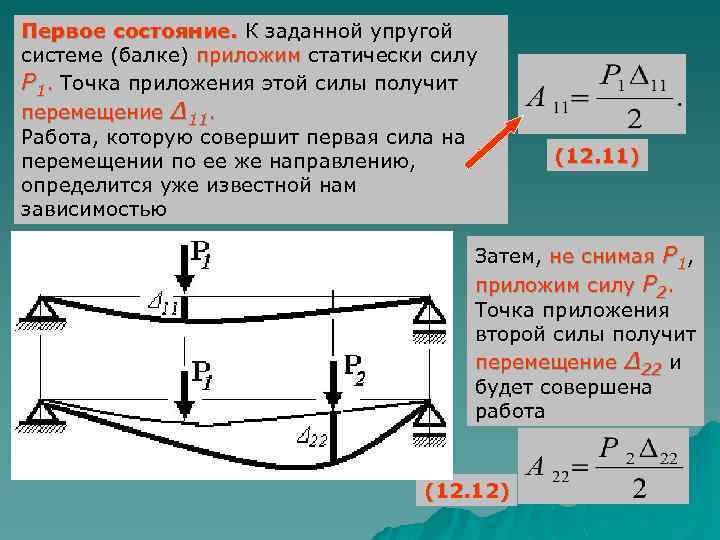Первое состояние. К заданной упругой системе (балке) приложим статически силу P 1. Точка приложения этой силы получит перемещение Δ 11. Работа, которую совершит первая сила на перемещении по ее же направлению, определится уже известной нам зависимостью (12. 11) Затем, не снимая P 1, приложим силу P 2. Точка приложения второй силы получит перемещение Δ 22 и будет совершена работа (12. 12)

Но система совершит также и дополнительную работу (силой P 1 на перемещении Δ 12 ). Для определения этой работы рассмотрим график зависимости перемещения от прикладываемой силы P=f(Δ). На втором этапе нагружения (силой Р 2), сила Р 1 по величине изменяться не будет, поэтому будет работа первой силы на перемещении по ее направлению от действия второй силы определится произведением (12. 13)

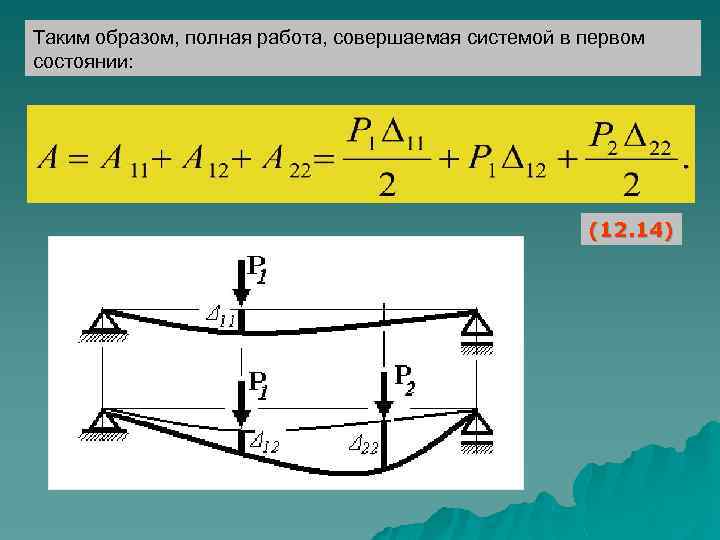Таким образом, полная работа, совершаемая системой в первом состоянии: (12. 14)

Второе состояние. Приложим силу P 2, а затем P 1. По аналогии с рассмотренным выше первым состоянием: (12. 15) Приравняем правые части выражений 12. 14 и 12. 15. Получим формулу:

Следовательно: (12. 16) Это есть математическая запись теоремы о взаимности работ и перемещений (теоремы Бэтти). Работа сил ПЕРВОГО состояния на перемещениях по их направлениям, вызванных силами ВТОРОГО состояния, равна работе сил ВТОРОГО состояния на перемещениях по их направлениям, вызванных силами ПЕРВОГО состояния.

12. 2. 2. Теорема о взаимности перемещений (теорема Максвелла) Если в обоих состояниях силы будут равны единице (P 1 будем иметь так называемые единичные состояния. = P 2 = 1), Перемещения от сил, равных единице, обозначим . Исходя из теоремы Бэтти (12. 16), получим теорему о взаимности перемещений (теорему Максвелла): (12. 17) Для ДВУХ ЕДИНИЧНЫХ СОСТОЯНИЙ упругой системы перемещение по направлению ПЕРВОЙ единичной силы, вызванное ВТОРОЙ единичной силой, равно перемещению по направлению ВТОРОЙ единичной силы, вызванному ПЕРВОЙ единичной силой.

Тогда перемещения от сил, не равных единице: (12. 18) Используя формулу для потенциальной энергии (12. 10), выразим составляющие работы силовые факторы. А (12. 14) через внутренние Учтем, что при прямом поперечном изгибе будут действовать только два силовых фактора – поперечная сила и изгибающий момент.

– полная работа А: совершается силами (P 1 + P 2) на перемещениях, вызванных этими же силами (12. 19) – составляющие работы, которую совершат соответственно силы Р 1 и Р 2 на перемещениях по своим направлениям (12. 20) (12. 21)

В этих формулах под символами M 1, M 2 и Q 1, Q 2 обозначены уравнения внутренних силовых факторов в поперечных сечениях от действующих сил. С другой стороны, в соответствии с формулами (12. 14, 12. 15): A = A 11 + A 22 + A 12 откуда A 12 = A – A 11 – A 22. С учетом выражений (12. 19 – 12. 21)

После преобразований получим: (12. 22) В формуле (12. 22) использованы следующие обозначения: – уравнения внутренних силовых факторов, возникающих в сечениях балки от действия сил первого состояния, – перемещения (деформации) элемента длиной dz, вызванные силами второго состояния.

В общем случае нагружения, с учетом теоремы Бэтти, получим формулу для определения работы, совершаемой силами первого состояния по направлениям сил второго состояния (и наоборот): (12. 23) ЭНЕРГЕТИЧЕСКИЙ ПОДХОД ДАЕТ ВОЗМОЖНОСТЬ ПОЛУЧИТЬ БОЛЕЕ ОБЩИЙ УНИВЕРСАЛЬНЫЙ МЕТОД ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ (в сравнении с методом начальных параметров).