12 3 ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ МЕТОДОМ МАКСВЕЛЛА-МОРА ИНТЕГРАЛ МОРА

12. 3. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ МЕТОДОМ МАКСВЕЛЛА-МОРА (ИНТЕГРАЛ МОРА)

Данный метод применяется ДЛЯ ВЫЧИСЛЕНИЯ ПЕРЕМЕЩЕНИЙ ПРОИЗВОЛЬНО НАГРУЖЕННЫХ БРУСЬЕВ С ЛЮБОЙ ФОРМОЙ ПОПЕРЕЧНОГО СЕЧЕНИЯ КАК С ПРЯМОЙ, ТАК И С КРИВОЙ ОСЬЮ.

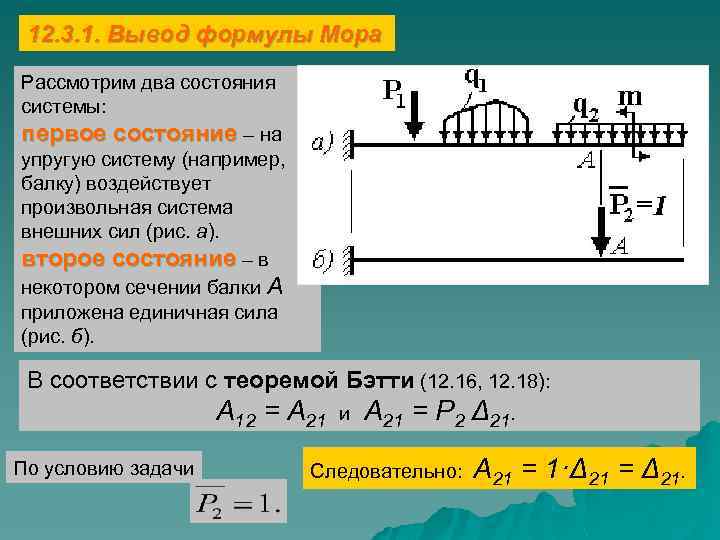12. 3. 1. Вывод формулы Мора Рассмотрим два состояния системы: первое состояние – на упругую систему (например, балку) воздействует произвольная система внешних сил (рис. а). второе состояние – в некотором сечении балки А приложена единичная сила (рис. б). В соответствии с теоремой Бэтти (12. 16, 12. 18): A 12 = A 21 и A 21 = P 2 Δ 21. По условию задачи Следовательно: A 21 = 1·Δ 21 = Δ 21.

Работа по направлению силы (во втором, единичном, состоянии) единичном от действия внешних нагрузок (от сил первого состояния) есть ПЕРЕМЕЩЕНИЕ в направлении ЕДИНИЧНОЙ силы (во втором состоянии) ОТ ДЕЙСТВИЯ ВНЕШНИХ СИЛ. При прямом поперечном (плоском) изгибе, с учетом равенства работ и в соответствии с формулой (12. 23): (12. 24)

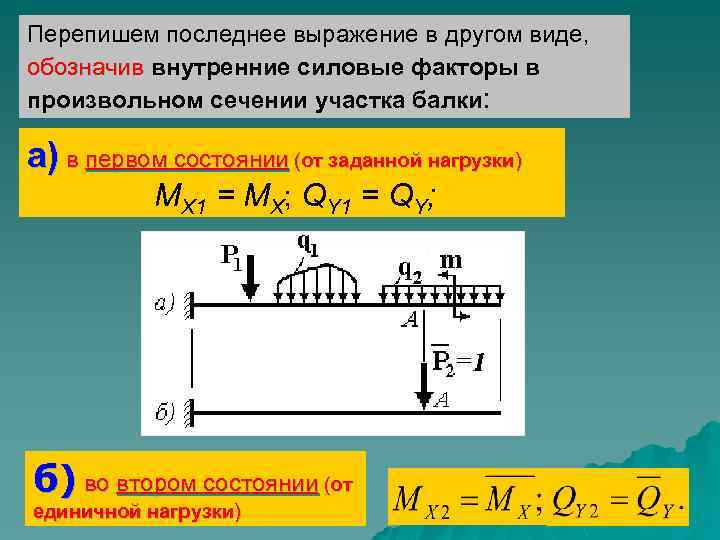Перепишем последнее выражение в другом виде, обозначив внутренние силовые факторы в произвольном сечении участка балки: а) в первом состоянии (от заданной нагрузки) MX 1 = MX; QY 1 = QY; б) во втором состоянии (от единичной нагрузки)

Δ 21 есть перемещение точки А (ΔА ) в направлении единичной силы Р 2 от действия внешних сил : (12. 25) При прямом поперечном (плоском) изгибе влияние поперечной силы на перемещения (прогиб и угол поворота) незначительно, поэтому второе слагаемое из записанной выше формулы можно исключить Получим следующую формулу: (12. 26) Интеграл, полученный в данном случае для плоского изгиба, называют интеграл Максвелла-Мора или интеграл Мора.

Аналогичные выражения можно получить для других простых видов нагружения, суммируя по участкам и интегрируя произведения уравнений силовых факторов, записываемых для грузовой и единичной схем, и характерных для рассматриваемого вида нагружения. В знаменатель подинтегральных выражений записывают жесткость сечения бруса, также характерную для рассматриваемого вида В случае сложного нагружения, используют нагружения. принцип независимости действия сил. Однако, определяя соответствующие перемещения, необходимо иметь в виду, что простое суммирование перемещений во многих случаях будет некорректным: например, угловые перемещения при изгибе и кручении происходят в разных

Для определения линейного перемещения (при прямом изгибе – прогиба) в исследуемом сечении в направлении этого перемещения прикладывают единичную силу Для определения углового перемещения (при прямом изгибе – угла поворота сечения) в его направлении прикладывают единичный момент

При растяжении (сжатии): При кручении: При сдвиге:

12. 3. 2. Порядок определения перемещений методом Мора 1. Изображается грузовая (заданная) схема с заданными нагрузками. Определяются опорные реакции. 2. Изображается единичная (вспомогательная) схема: по направлению искомого перемещения прикладывается единичная нагрузка. Определяются опорные реакции. Направление силы или момента, принимаемое в единичной схеме значения не имеет. Если в результате расчета получим минус, то это означает то, что действительное направление перемещения будет противоположно принятому в единичной

3. Грузовая и единичная схемы разбиваются на участки так, чтобы границы этих участков были ОБЩИМИ для обеих схем. При этом необходимо учитывать также возможное изменение размеров или формы сечения и свойств материала бруса. 4. При определении перемещений при прямом изгибе составляются уравнения изгибающего момента в произвольном сечении каждого участка от заданных нагрузок и от единичной нагрузки (для грузовой и единичной схем). схем 5. Выражения М и (без подстановки значений границ участков!) подставляются в формулу участков! интеграла Мора (12. 26) и определяется искомое перемещение. 6. Интегрирование ведется по участкам. Пределы интегрирования – значения длин этих

12. 3. 3. Пример Определить перемещение конца стержня А при его осевом растяжении центрально приложенной силой. При осевом растяжении в поперечном сечении N, которые вызывают осевое же перемещение сечения А стержня возникают продольные силы (абсолютную линейную деформацию стержня). В соответствии с законом Гука, эта деформация определяется по известной формуле: В соответствии с формулой Мора, для определения перемещения сечения А дополнительно к грузовой схеме изобразим единичную схему: Δℓ в сечении А приложим силу, равную единице и направим ее вдоль оси

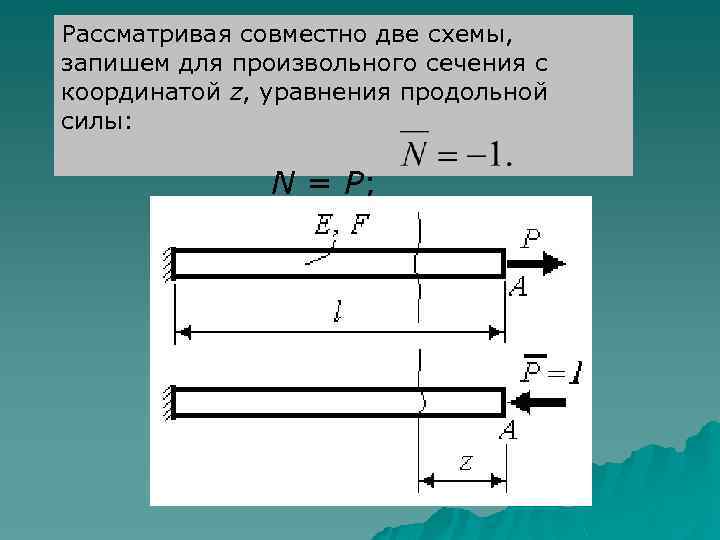Рассматривая совместно две схемы, запишем для произвольного сечения с координатой z, уравнения продольной силы: N = P;

Тогда Полученное выражение соответствует формуле закона Гука. Минус указывает на то, что сечение А будет перемещаться в сторону, противоположную принятому в единичной схеме направлению единичной силы.

12. 4. Способ Верещагина

Техника вычисления перемещений методом (интегралом) Мора может быть упрощена при использовании графо-аналитического приема, называемого «способ перемножения эпюр» или способ (правило) Верещагина. Этот метод назван в честь его автора – студента Московского института инженеров транспорта А. Верещагина, предложенного им в 1925 г. Метод Верещагина является частным случаем определения перемещений интегрированием по Мору и позволяет операцию интегрирования заменить перемножением эпюр в соответствии с зависимостью, называемой формула Верещагина. Ограничения: – жесткость бруса (при изгибе EI) на каждом участке его должна быть постоянной; – единичная эпюра всегда должна очерчиваться прямой линией (для бруса с прямой осью это будет всегда!). всегда! Если обе эпюры криволинейны, их перемножать по способу Верещагина нельзя.

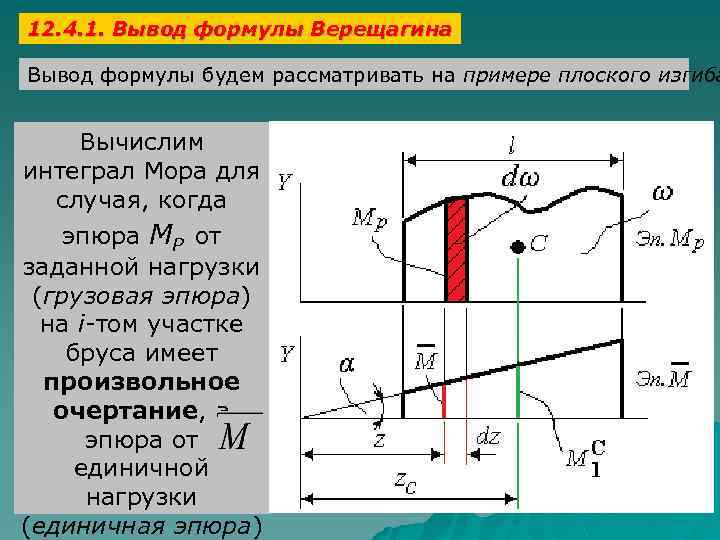12. 4. 1. Вывод формулы Верещагина Вывод формулы будем рассматривать на примере плоского изгиба Вычислим интеграл Мора для случая, когда эпюра MР от заданной нагрузки (грузовая эпюра) на i-том участке бруса имеет произвольное очертание, а эпюра от единичной нагрузки (единичная эпюра)

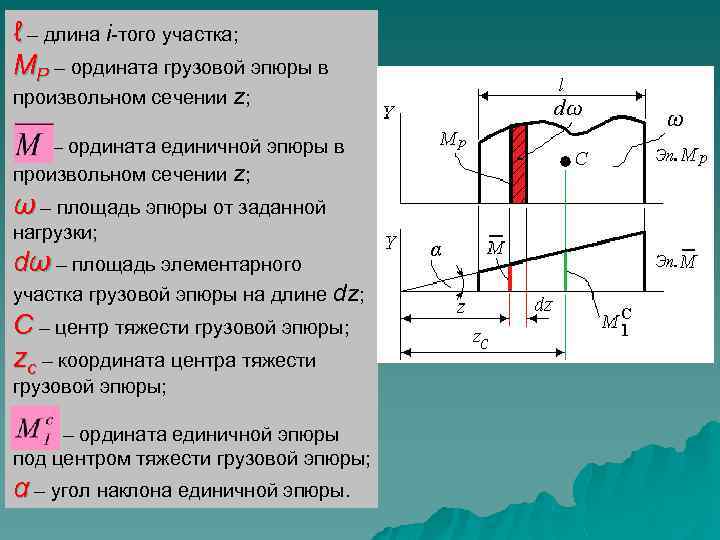ℓ – длина i-того участка; МР – ордината грузовой эпюры в произвольном сечении z; – ордината единичной эпюры в произвольном сечении z; ω – площадь эпюры от заданной нагрузки; dω – площадь элементарного участка грузовой эпюры на длине dz; С – центр тяжести грузовой эпюры; zс – координата центра тяжести грузовой эпюры; – ордината единичной эпюры под центром тяжести грузовой эпюры; α – угол наклона единичной эпюры.

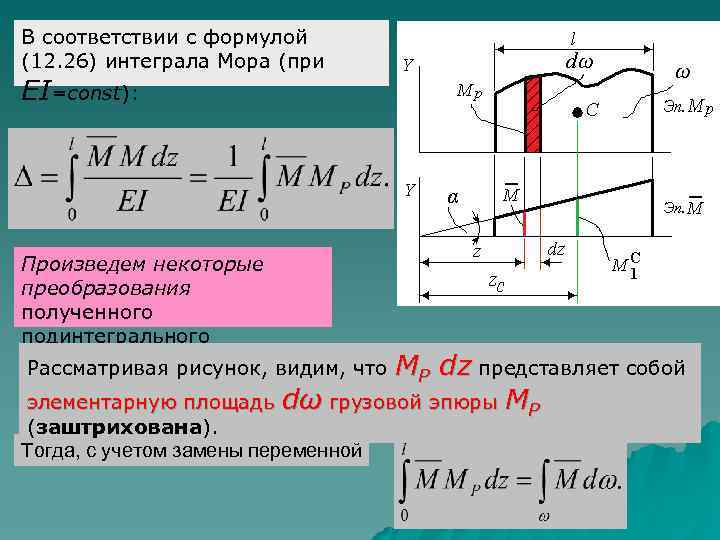В соответствии с формулой (12. 26) интеграла Мора (при EI=const): Произведем некоторые преобразования полученного подинтегрального выражения. Рассматривая рисунок, видим, что MР dz представляет собой элементарную площадь dω грузовой эпюры МР (заштрихована). Тогда, с учетом замены переменной

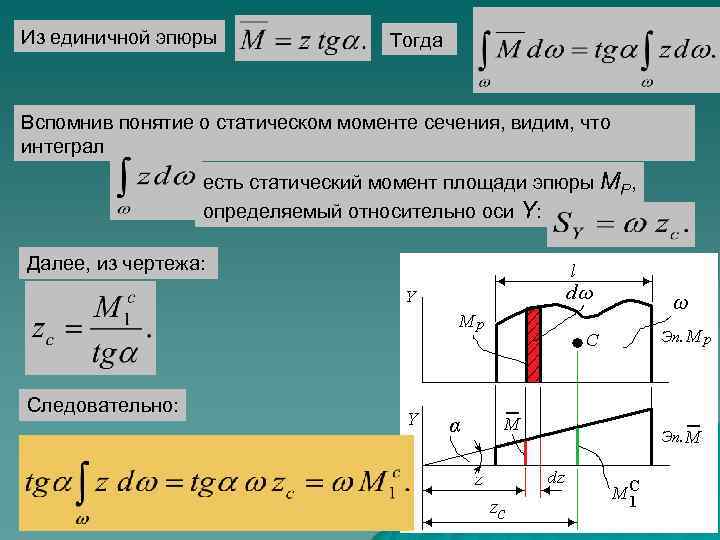Из единичной эпюры Тогда Вспомнив понятие о статическом моменте сечения, видим, что интеграл есть статический момент площади эпюры МР, определяемый относительно оси Y: Далее, из чертежа: Следовательно:

Окончательно формула для определения перемещений при изгибе по способу Верещагина имеет вид: (12. 27) Данное выражение носит название формула Верещагина. Результат перемножения положителен, если эпюры расположены по одну сторону от оси и отрицателен, если они расположены по разные стороны от оси. Для определения перемещений при других видах нагружения бруса необходимо перемножать эпюры (грузовую и единичную), построенные для соответствующих внутренних силовых факторов

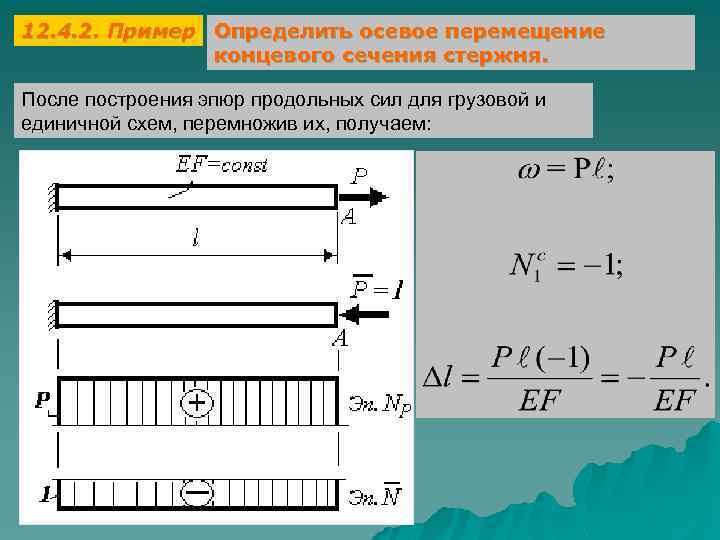12. 4. 2. Пример Определить осевое перемещение концевого сечения стержня. После построения эпюр продольных сил для грузовой и единичной схем, перемножив их, получаем:

12. 4. 3. Порядок определения перемещений по Верещагину 1. Изобразить заданную схему со всеми приложенными нагрузками. Определить опорные реакции, построить эпюру изгибающих моментов (грузовую эпюру). 2. Изобразить единичную (вспомогательную) схему. Определить опорные реакции, построить эпюру изгибающих моментов (единичную эпюру). 3. Рассмотреть построенные эпюры совместно и определить общие границы участков. При этом необходимо учитывать также возможное изменение от участка к участку размеров или формы сечения и свойств материала бруса.

4. Определить на каждом участке: • площадь грузовой эпюры; • положение центра тяжести площади вдоль оси эп • спроецировать центр тяжести на единичную эпюру; • определить ординату единичной эпюры. 5. Перемножить в соответствии с формулой Верещагина (12. 27) полученные значения (говорят: перемножить эпюры по способу Верещагина) и определить искомое Верещагина перемещение. Если балка состоит из нескольких участков, то эпюры перемножают по участкам и результат алгебраически складывают.

Если перемножаемые эпюры имеют сложные очертания, при которых затруднительно найти положение центра тяжести и площадь, то эти эпюры разбивают на простейшие фигуры (прямоугольники, треугольники, параболические сегменты), для которых легко определяются площадь и положение центра тяжести грузовой эпюры и соответствующие ординаты единичных эпюр.

12. 4. 4. Рекомендации по перемножению эпюр Рассмотрим подробнее особенности разбиения эпюр, наиболее часто встречающихся в расчетной практике. На произвольном участке балки эпюра изгибающих моментов может очерчиваться различными линиями На рисунках знаки ординат не проставлены, они соответствуют правилу знаков для изгибающих моментов.

ПАРАБОЛИЧЕСК ИЙ СЕГМЕНТ Площадь сегмента q – значение интенсивности равномерно распределенной нагрузки, Н/м, ℓ – длина участка балки, к которой приложена эта нагрузка. Центр тяжести площади располагается посередине участка, на котором приложена нагрузка.

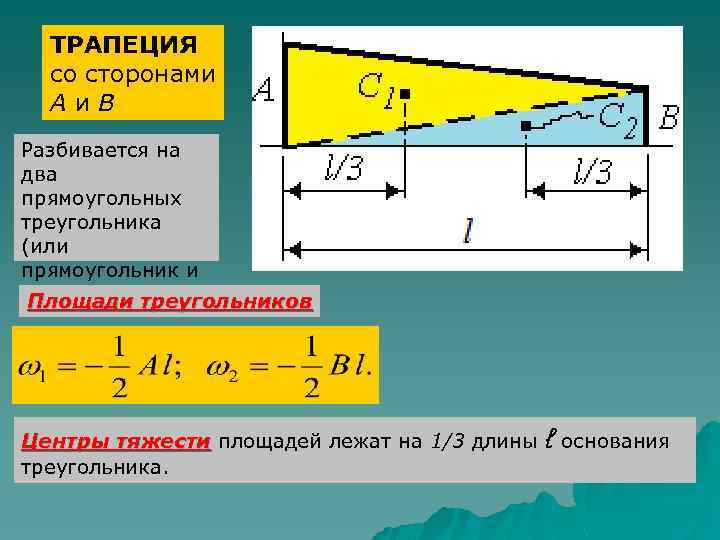ТРАПЕЦИЯ со сторонами Аи. В Разбивается на два прямоугольных треугольника (или прямоугольник и треугольник) Площади треугольников Центры тяжести площадей лежат на 1/3 длины треугольника. ℓ основания

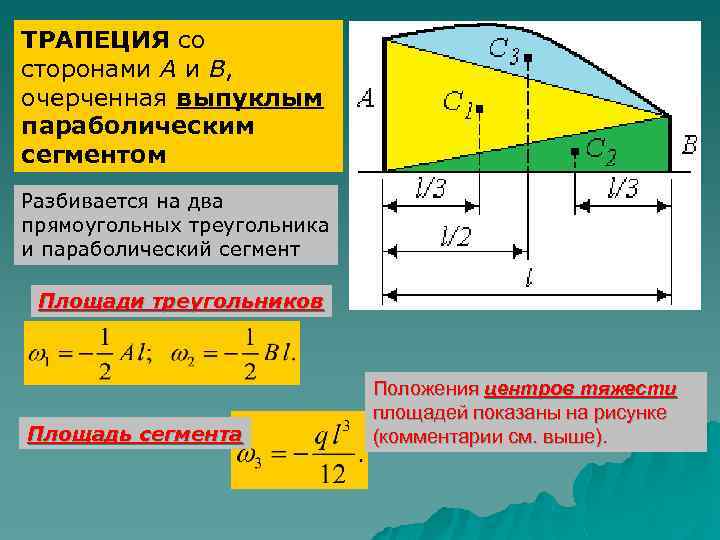ТРАПЕЦИЯ со сторонами А и В, очерченная выпуклым параболическим сегментом Разбивается на два прямоугольных треугольника и параболический сегмент Площади треугольников Площадь сегмента Положения центров тяжести площадей показаны на рисунке (комментарии см. выше).

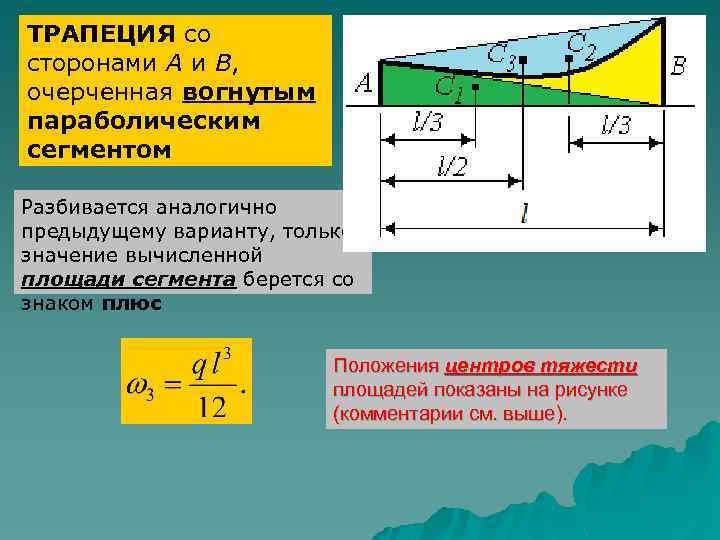ТРАПЕЦИЯ со сторонами А и В, очерченная вогнутым параболическим сегментом Разбивается аналогично предыдущему варианту, только значение вычисленной площади сегмента берется со знаком плюс Положения центров тяжести площадей показаны на рисунке (комментарии см. выше).

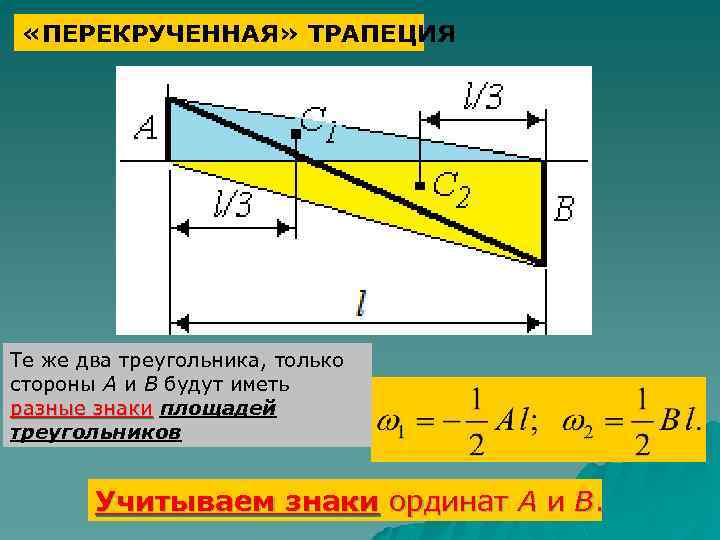«ПЕРЕКРУЧЕННАЯ» ТРАПЕЦИЯ Те же два треугольника, только стороны А и В будут иметь разные знаки площадей треугольников Учитываем знаки ординат А и В.

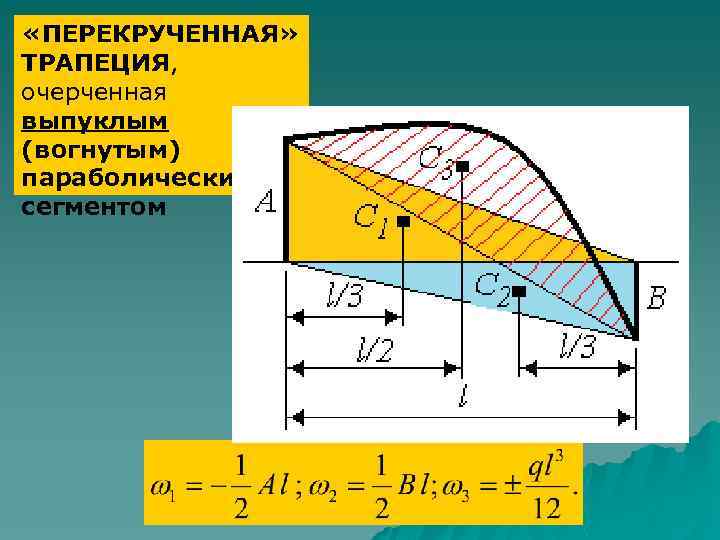«ПЕРЕКРУЧЕННАЯ» ТРАПЕЦИЯ, очерченная выпуклым (вогнутым) параболическим сегментом

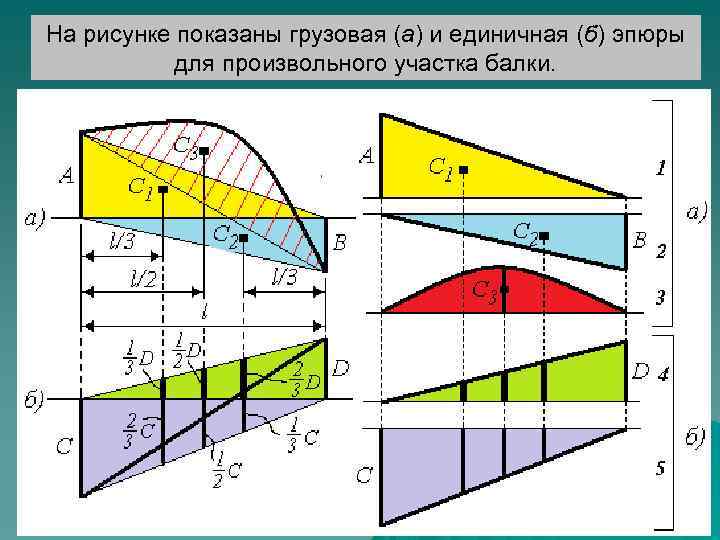На рисунке показаны грузовая (а) и единичная (б) эпюры для произвольного участка балки.

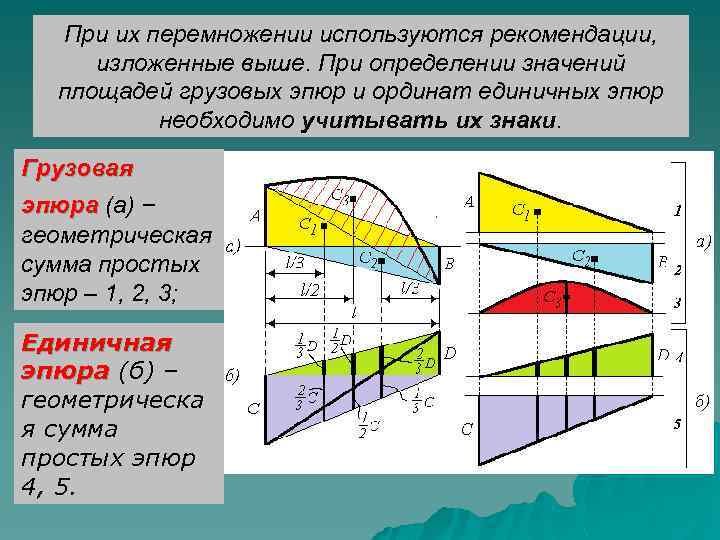При их перемножении используются рекомендации, изложенные выше. При определении значений площадей грузовых эпюр и ординат единичных эпюр необходимо учитывать их знаки. Грузовая эпюра (а) – геометрическая сумма простых эпюр – 1, 2, 3; Единичная эпюра (б) – геометрическа я сумма простых эпюр 4, 5.

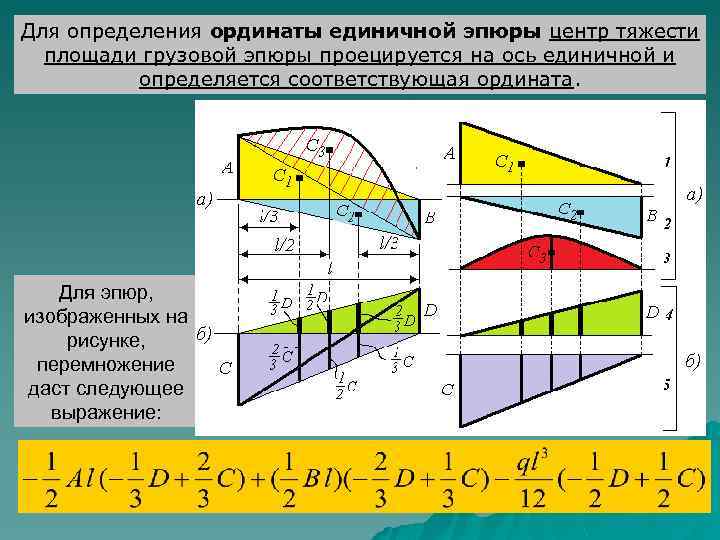Для определения ординаты единичной эпюры центр тяжести площади грузовой эпюры проецируется на ось единичной и определяется соответствующая ордината. Для эпюр, изображенных на рисунке, перемножение даст следующее выражение:

В курсе «Строительная механика» широко используется формула, которая дает возможность определять перемещения перемножением эпюры, не проводя построений, показанных на рисунке (формула Симпсона): Симпсона (12. 28) Ординаты на границах участка (A, B, C, D) подставляются в приведенную выше формулу со своими знаками. Для выпуклого параболического сегмента ставят знак (–), а для вогнутого – знак (+). При перемножении эпюр также можно пользоваться данными, приведенными в таблице (следующий слайд).

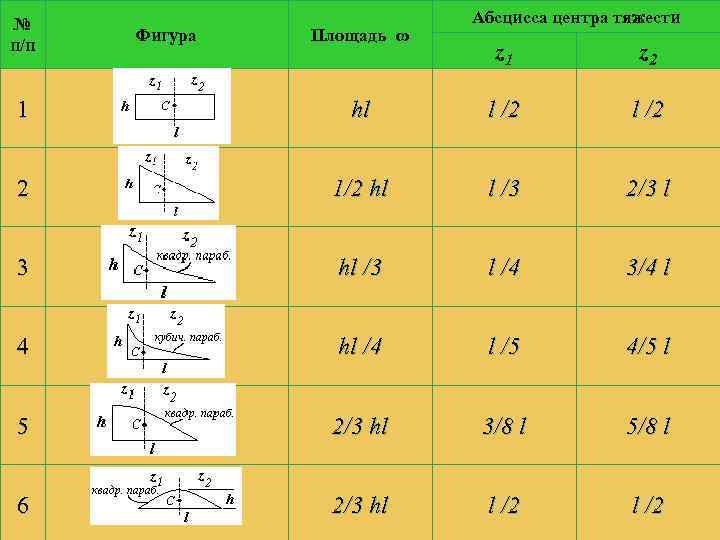№ п/п Фигура Площадь ω Абсцисса центра тяжести z 1 z 2 1 hl l /2 2 1/2 hl l /3 2/3 l 3 hl /3 l /4 3/4 l 4 hl /4 l /5 4/5 l 5 2/3 hl 3/8 l 5/8 l 6 2/3 hl l /2