12. 2 – Conditional Probability
Conditional Probability n n Conditional Probability contains a condition that may limit the sample space for an event. You can write a conditional probability using the notation - This reads “the probability of event B, given event A”
Conditional Probability The table shows the results of a class survey. Find P(own a pet | female) Do you own a pet? yes female 8 male 5 no 6 7 14 females; 13 males The condition female limits the sample space to 14 possible outcomes. Of the 14 females, 8 own a pet. Therefore, P(own a pet | female) equals 8. 14
Conditional Probability The table shows the results of a class survey. Find P(wash the dishes | male) Did you wash the dishes last night? yes no 13 females; female 7 6 15 males male 7 8 The condition male limits the sample space to 15 possible outcomes. Of the 15 males, 7 did the dishes. Therefore, P(wash the dishes | male) 7 15
Let’s Try One Using the data in the table, find the probability that a sample of not recycled waste was plastic. P(plastic | non-recycled) The given condition limits the sample space to non-recycled waste. A favorable outcome is non-recycled plastic. Material Recycled Paper 34. 9 Metal 6. 5 Glass 2. 9 Plastic 1. 1 Other 15. 3 Not Recycled 48. 9 10. 1 9. 1 20. 4 67. 8 20. 4 48. 9 + 10. 1 + 9. 1 + 20. 4 + 67. 8 20. 4 = 156. 3 0. 13 The probability that the non-recycled waste was plastic is about 13%. P(plastic | non-recycled) =
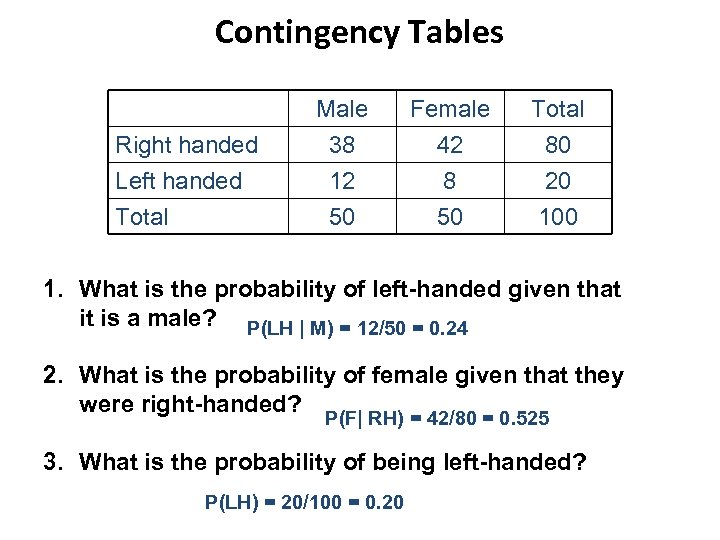
Contingency Tables Right handed Left handed Total Male 38 12 50 Female 42 8 50 Total 80 20 100 1. What is the probability of left-handed given that it is a male? P(LH | M) = 12/50 = 0. 24 2. What is the probability of female given that they were right-handed? P(F| RH) = 42/80 = 0. 525 3. What is the probability of being left-handed? P(LH) = 20/100 = 0. 20
Conditional Probability Formula n For any two events A and B from a sample space with P(A) does not equal zero
Examples n In a school, the probability that a freshman takes Math 1 and Math 2 during the same semester is 0. 25. The probability that a freshman takes Math 1 is 0. 72. What is probability that a freshman takes Math 2 given that they have already took Math 1.
Example n The probability of going to the store and not buying any items is. 42. The probability of not buying any items is. 75. Find the probability of going to the store given that you did not buy any items.
Probability of A and B If A and B are independent events, then P(A and B)= P(A) · P(B) If A and B are NOT independent events, then P (A and B) =
Probability of A or B If A and B are mutually exclusive, then P(A or B) = P(A) + P(B) If A and B are not mutually exclusive, then P(A or B) = P(A) + P(B) - P(A and B) Mutually Exclusive means they can not occur at the same time
Mutually exclusive outcomes A pupil is chosen at random from the class. Which of the following pairs of outcomes are mutually exclusive? Outcome A: the pupil has brown eyes. Outcome B: the pupil has blue eyes. These outcomes are mutually exclusive because a pupil can either have brown eyes, blue eyes or another colour of eyes. Outcome C: the pupil has black hair. Outcome D: the pupil has wears glasses. These outcomes are not mutually exclusive because a pupil could have both black hair and wear glasses.
Example 2 Given that P(A) =. 3 , P(B) =. 6, and P(B|A) =. 4 find: a) P(A and B) P(B|A) = --------- so P(A and B) = P(B|A) • P(A) P(A and B) = 0. 4 • 0. 3 = 0. 12 b) P(A or B) If A and B are not mutually exclusive P(A or B) = P(A) + P(B) – P(A and B) = 0. 3 + 0. 4 – 0. 12 = 0. 58 c) P(A|B) P(A and B) 0. 12 P(A|B) = --------- = 0. 2 P(B) 0. 6
Example 4 If 60% of a department store’s customers are female and 75% of the female customers have a store charge card, what is the probability that a customer selected at random is female and had a store charge card? Let A = female customer and let B = customer has a store charge card P(A and B) P(B|A) = --------- so P(A and B) = P(B|A) • P(A) P(A and B) = 0. 75 • 0. 6 = 0. 45
Example 3 Given P(A | B) = 0. 55 and P(A or B) = 0. 64 and P(B) = 0. 3. Find P(A). P(A and B) P(A|B) = --------- so P(A and B) = P(A|B) • P(B) P(A and B) = 0. 55 • 0. 3 = 0. 165 P(A or B) = P(A) + P(B) – P(A and B) P(A) = P(A or B) – P(B) + P(A and B) = 0. 64 – 0. 3 + 0. 165 = 0. 505
Скачать презентацию 12 2 Conditional Probability Conditional Probability
6323101c19cbc5d56faacc03fe1bdcac.ppt