11 СЛОЖНОЕ СОПРОТИВЛЕНИЕ БРУСА Рассмотрим общий случай

11. СЛОЖНОЕ СОПРОТИВЛЕНИЕ БРУСА

Рассмотрим общий случай действия сил на брус. К сложным видам нагружения (сложному сопротивлению) относятся виды нагружения, при которых в поперечном сечении бруса возникает не менее двух внутренних силовых факторов, одновременно учитываемых при расчетах на прочность и жесткость.

Алгоритм решения задачи остается прежним (тем, который применялся при рассмотрении простых видов нагружения): – строятся эпюры внутренних силовых факторов; – определяется вид нагружения и опасное (или опасные) сечение бруса; – записывается условие прочности (или условие жесткости); – решается задача (проверка прочности, проектировочный расчет или определение допускаемой нагрузки). При анализе сложного сопротивления материала бруса используется также принцип независимости действия сил (принцип суперпозиции).

Рассмотрим наиболее часто встречающиеся в расчетной практике виды сложного сопротивления: – косой изгиб; – изгиб с кручением; – внецентренное растяжение (сжати – расчет цилиндрических пружин.

11. 1. Косой изгиб

Косым изгибом называют такой вид нагружения бруса, при котором внешние нагрузки, вызывающие его изгиб, не лежат ни в одной из главных центральных плоскостей инерции поперечного сечения бруса. Иначе говоря, силовая плоскость не совпадает ни с одной из главных центральных плоскостей инерции сечения. Как известно, при прямом поперечном изгибе в сечениях бруса действуют поперечная сила и изгибающий момент: от вертикальной нагрузки Qy и Mx; от горизонтальной нагрузки Qx и My.

Рассмотрим консольную балку, защемленную одним концом, и нагруженную на другом силой Р. Эта сила приложена в плоскости поперечного сечения балки. Она может быть направлена вертикально, горизонтально или под некоторым углом оси сечения. αк

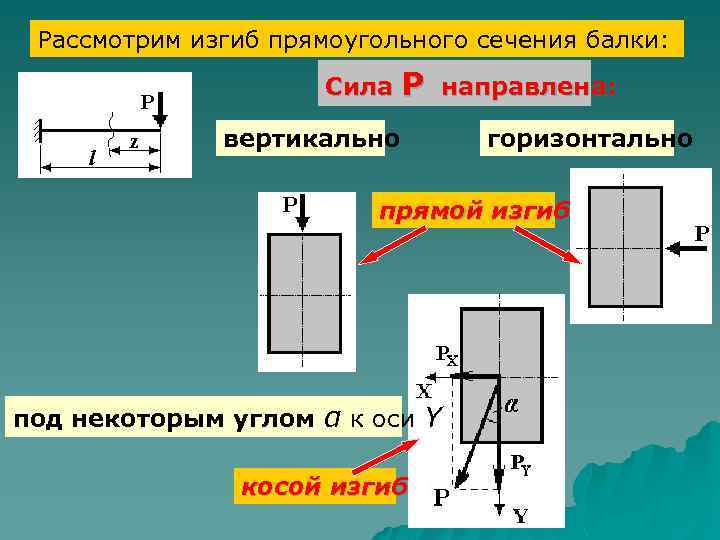
Рассмотрим изгиб прямоугольного сечения балки: Сила Р вертикально направлена: горизонтально прямой изгиб под некоторым углом α к оси Y косой изгиб

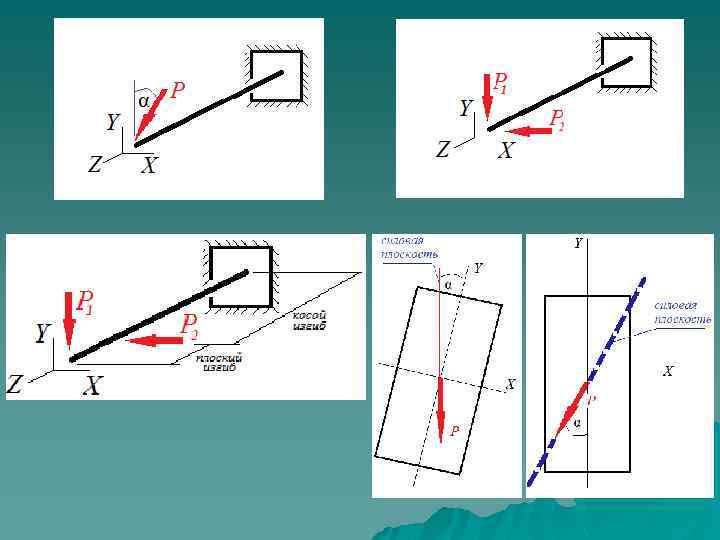
Легко видеть, что косой изгиб может быть представлен комбинацией прямых изгибов от действия проекций силы на координатные оси. Анализ напряженно-деформированного состояния ведем в ГЛАВНЫХ ЦЕНТРАЛЬНЫХ ОСЯХ поперечного сечения бруса.

Направление главных центральных осей X и Y выбираем таким, чтобы сила Р лежала в первом квадранте координатной системы. Величина нормальных напряжений от действия изгибающего момента намного больше величины касательных напряжений от поперечной силы. Поэтому влиянием поперечных сил пренебрегаем.

Условие прочности, как известно, записывается для опасных точек сечения (точек с экстремальными значениями величин нормальных напряжений). Следовательно, необходимо найти положение этих точек. Для этого необходимо: а) получить формулу для вычисления нормального напряжения в любой точке произвольного сечения, отстоящего на расстоянии z от свободного конца балки; б) определить положение нейтральной оси; в) найти точки, наиболее удаленные от нейтральной линии, для которых следует записать условие прочности.

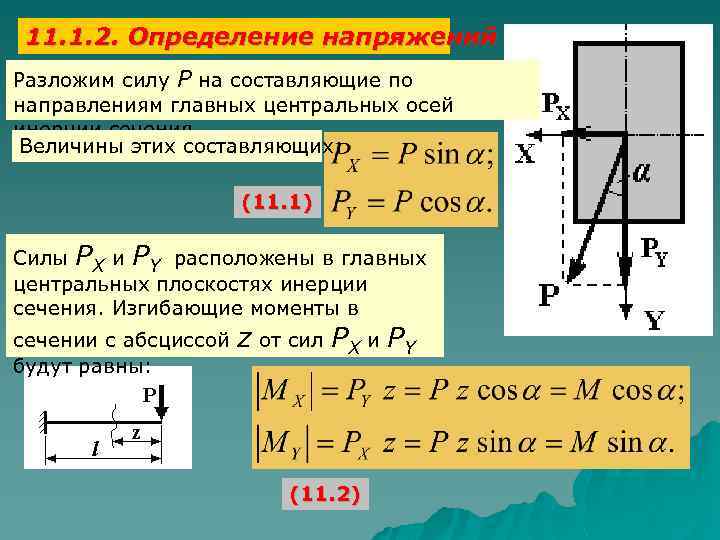
11. 1. 2. Определение напряжений Разложим силу Р на составляющие по направлениям главных центральных осей инерции сечения. Величины этих составляющих: (11. 1) Силы PX и PY расположены в главных центральных плоскостях инерции сечения. Изгибающие моменты в сечении с абсциссой будут равны: z от сил РX и РY (11. 2)

На основании принципа независимости действия сил нормальные напряжения в рассматриваемом поперечном сечении будут равны сумме нормальных напряжений от раздельного действия моментов М X и М Y: (11. 3) Нормальные напряжения при прямом изгибе определяются по формуле Навье. Следовательно, для любой точки сечения в общем случае мы можем записать: (11. 4)

Если плоскость действия сил в сечении проходит через первый квадрант, то знак перед слагаемыми необходимо назначить по тому действию, которое вызывает изгибающий момент (по правилу знаков для изгибающего момента). Тогда для получения по формуле (11. 4) правильного знака в любой точке сечения, достаточно учесть знаки координат этой точки х и у. В формулу (11. 4) вместо МX и МY подставим их выражения из формул (11. 1, 11. 2). Получим формулу дл расчета нормальных напряжений при косом изгибе.

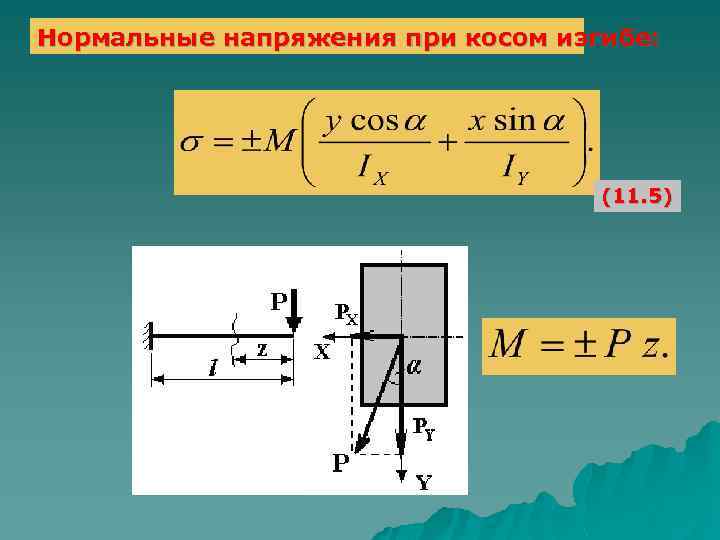
Нормальные напряжения при косом изгибе: (11. 5)

11. 1. 2. Положение нейтральной линии При прямом изгибе нейтральная линия, как известно, проходит через центр тяжести поперечного сечения балки и перпендикулярна силовой плоскости. Предположим, что нейтральная линия в поперечном сечении бруса при косом изгибе не перпендикулярна плоскости действия изгибающего момента – силовой плоскости По формуле (11. 5), при х=0 и у=0, получаем 0. Следовательно, при косом изгибе, как и прямом, нейтральная линия проходит через центр тяжести поперечного сечения.

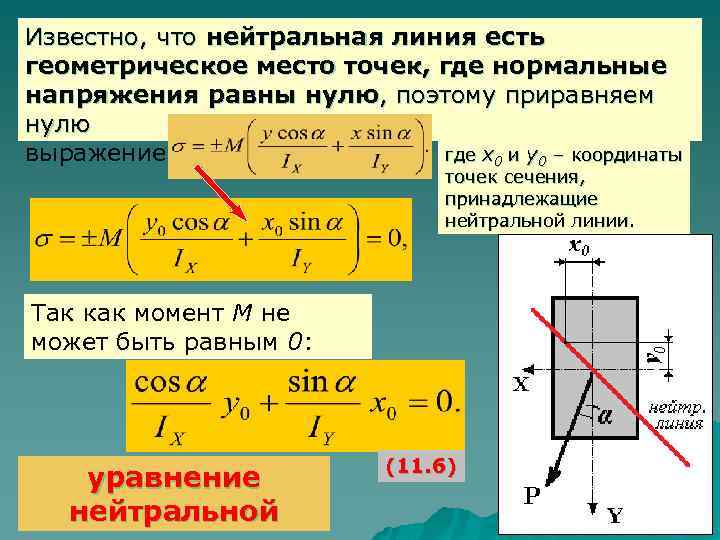
Известно, что нейтральная линия есть геометрическое место точек, где нормальные напряжения равны нулю, поэтому приравняем нулю выражение где x 0 и y 0 – координаты точек сечения, принадлежащие нейтральной линии. Так как момент М не может быть равным 0: уравнение нейтральной (11. 6)

После преобразования уравнения нейтральной линии получим: Тангенс угла β наклона нейтральной линии к оси X (отсчет угла β ведется по ходу часовой стрелки): Следовательно:

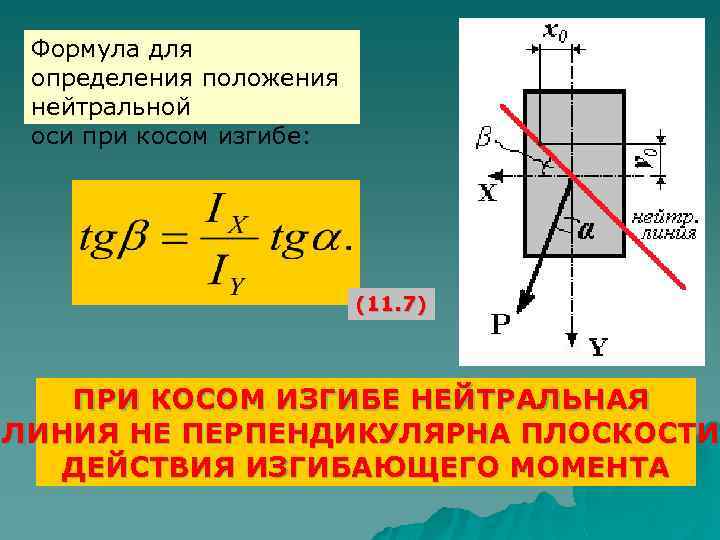
Формула для определения положения нейтральной оси при косом изгибе: (11. 7) ПРИ КОСОМ ИЗГИБЕ НЕЙТРАЛЬНАЯ ЛИНИЯ НЕ ПЕРПЕНДИКУЛЯРНА ПЛОСКОСТИ ДЕЙСТВИЯ ИЗГИБАЮЩЕГО МОМЕНТА

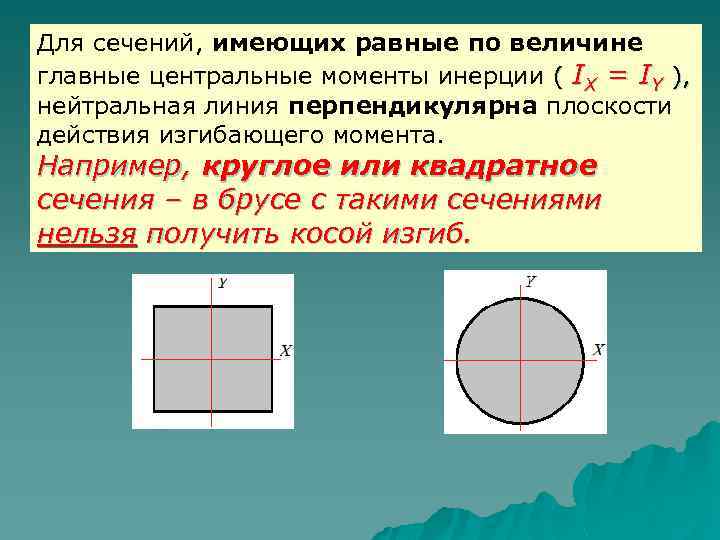
Для сечений, имеющих равные по величине главные центральные моменты инерции ( IX = IY ), нейтральная линия перпендикулярна плоскости действия изгибающего момента. Например, круглое или квадратное сечения – в брусе с такими сечениями нельзя получить косой изгиб.

Этого не скажешь о равнобоком уголке, даже если сила будет приложена в центре тяжести сечения: оси X, Y не являются главными центральными осями. В сечении «равнобокий уголок» главные центральные оси U и V проходят под углом 450 по отношению к центральным осям X и Y. Центральные оси X и Y параллельны полкам уголка. Центральные моменты инерции IX и IY равны по величине. Главные центральные моменты инерции – IU и IV не равны по величине

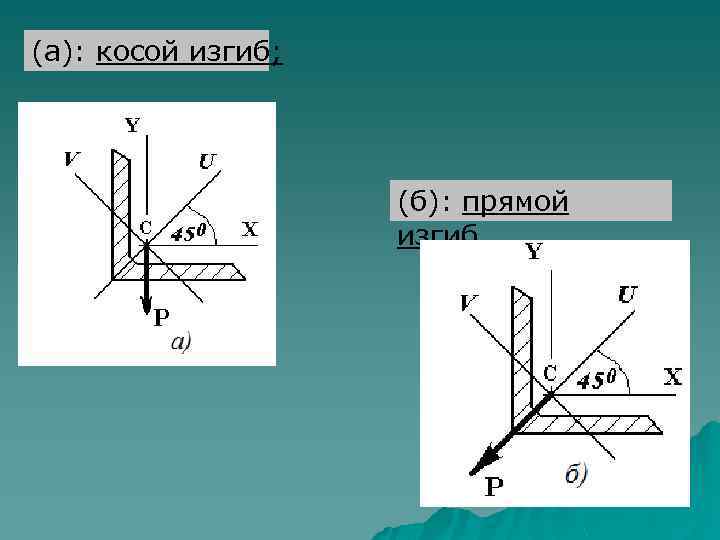
(а): косой изгиб; (б): прямой изгиб.

11. 1. 3. Определение опасных точек сечения Для сечений, имеющих две оси симметрии и выступающие углы (прямоугольник, квадрат, двутавра), определение опасных точек сечения не вызывает затруднений. Для этих точек нормальные напряжения будут равны соответственно (формула 11. 5): В рассматриваемом примере (прямоугольное сечение) опасными точками будут точки А и С, как наиболее удаленные от нейтральной линии.

В приведенных выше формулах точки А и С наиболее удалены от нейтральной линии, т. е. имеют соответствующие координаты xmax и ymax (отсюда переход в этих формулах от моментов инерции к моментам сопротивления). 11. 1. 4. Условие прочности Построим эпюру нормальных напряжений для прямоугольного сечения. Для равнопрочного материала (пластичного), обе точки (А и С) являются одинаково опасными: (11. 8)

Если же материал неравнопрочен (хрупкий), т. е хуже сопротивляется растяжению, чем сжатию, то более опасной будет точка С, где действуют наибольшие растягивающие напряжения. Условие прочности для точки С: (11. 9) Следует иметь в виду, что изгибающие моменты в опасном сечении могут иметь не экстремальные, а близкие к ним значения.

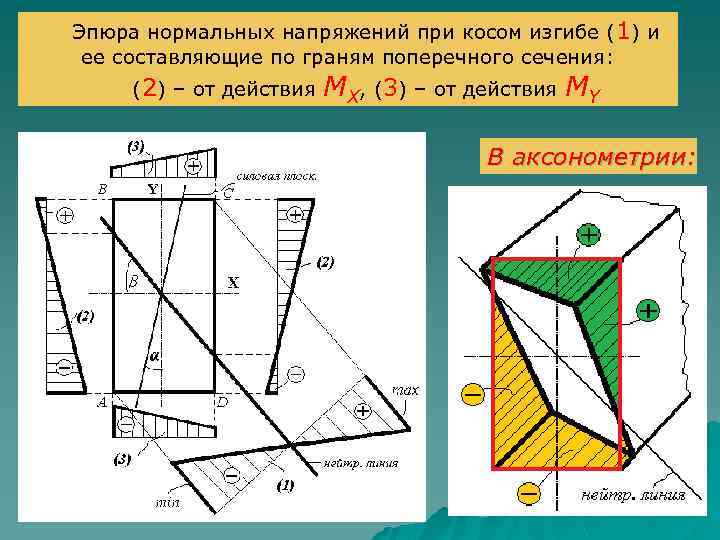
Эпюра нормальных напряжений при косом изгибе (1) и ее составляющие по граням поперечного сечения: (2) – от действия MX, (3) – от действия MY В аксонометрии:

В случаях, когда положение опасных точек сечения не очевидно (тавр, уголок, швеллер), необходимо провести простейший анализ: 1) определить положение нейтральной линии; 2) установить положение опасных точек; 3) определить нормальные напряжения σ по общим уравнениям и сравнить с допускаемым. (11. 10) Нормальные напряжения при косом изгибе могут значительно отличаться от напряжений при прямом изгибе, вызванных изгибающим моментом такой же величины, но действующим в плоскости, которая перпендикулярна главной центральной оси инерции.

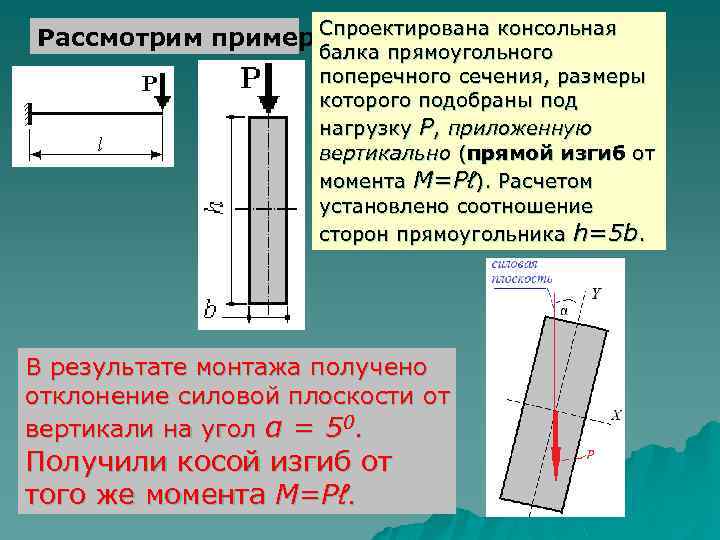
Рассмотрим пример. Спроектирована консольная балка прямоугольного поперечного сечения, размеры которого подобраны под нагрузку Р, приложенную вертикально (прямой изгиб от момента M=Pℓ). Расчетом установлено соотношение сторон прямоугольника h=5 b. В результате монтажа получено отклонение силовой плоскости от вертикали на угол α = 50. Получили косой изгиб от того же момента M=Pℓ.

Отношение осевых моментов сопротивления заданного сечения Максимальные нормальные напряжения Отклонение плоскости действия момента от оси Y на 50 приводит к увеличению максимальных напряжений на 43% по сравнению с прямым изгибом моментом той же величины.

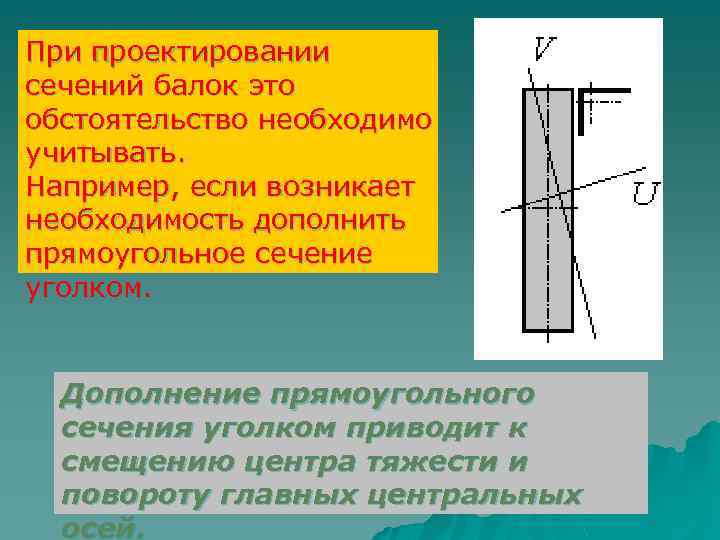
При проектировании сечений балок это обстоятельство необходимо учитывать. Например, если возникает необходимость дополнить прямоугольное сечение уголком. Дополнение прямоугольного сечения уголком приводит к смещению центра тяжести и повороту главных центральных осей.

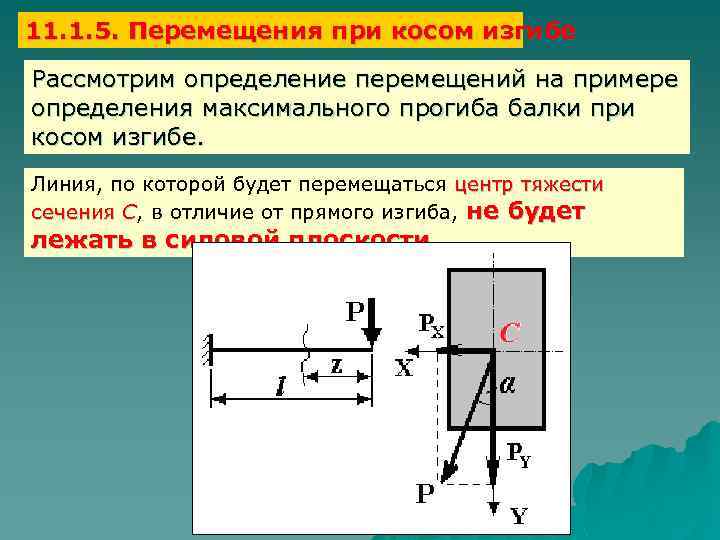
11. 1. 5. Перемещения при косом изгибе Рассмотрим определение перемещений на примере определения максимального прогиба балки при косом изгибе. Линия, по которой будет перемещаться центр тяжести сечения С, в отличие от прямого изгиба, не будет лежать в силовой плоскости.

Полный прогиб балки f, в соответствии с принципом суперпозиции, определим геометрической суммой прогибов в вертикальном v и горизонтальном u направлениях: Составляющие полного прогиба определим методом начальных параметров. Аналогично будет решаться задача по определению углов поворота.

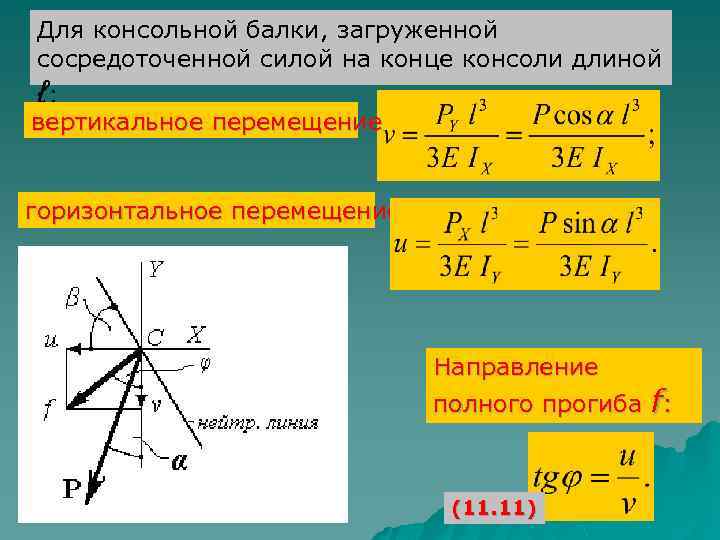
Для консольной балки, загруженной сосредоточенной силой на конце консоли длиной ℓ: вертикальное перемещение горизонтальное перемещение Направление полного прогиба f: (11. 11)

С учетом значений составляющих полного прогиба, после простых преобразований: Это есть уравнение, по которому определяется направление полного перемещения центра тяжести сечения при косом изгибе. получаем равенство Принимая во внимание, что tgφ = tgβ(11. 12). Отсюда следует, что углы φ и β равны между собой. ЦЕНТР ТЯЖЕСТИ СЕЧЕНИЯ ПРИ КОСОМ ИЗГИБЕ ПЕРЕМЕЩАЕТСЯ ПЕРПЕНДИКУЛЯРНО НЕЙТРАЛЬНОЙ ЛИНИИ.