11 ИССЛЕДОВАНИЕ ВЗАИМОСВЯЗЕЙ СОЦИАЛЬНО-ЭКОНОМИЧЕС КИХ ЯВЛЕНИЙ 1. 1.

11 ИССЛЕДОВАНИЕ ВЗАИМОСВЯЗЕЙ СОЦИАЛЬНО-ЭКОНОМИЧЕС КИХ ЯВЛЕНИЙ 1. 1. Виды и формы связи между явлениями 2. 2. Приемы изучения связи 3. 3. Корреляционно-регрессионный анализ: задачи и виды 4. 4. Определение формы взаимосвязи 5. 5. Измерение тесноты связи

Признаки единиц совокупности могут быть взаимосвязанными: Результативные (аналог зависимой переменной Y в математике); Факторные — под их воздействием изменяются результативные (аналог независимой переменной X в математике). 1. 1. Виды и формы связи между явлениями

3 Виды связи 1. Функциональная — каждому значению факторного признака соответствует определённое значение результативного; для выявления такой связи достаточно одного наблюдения. 2. Стохастическая — связь между случайными величинами.

4 Виды связи 2. Стохастическая : статистическая – одному и тому же значению факторного признака может соответствовать несколько значений результативного признака. Проявляются только для большого числа единиц совокупности. корреляционная – одному и тому же значению факторного признака соответствует несколько значений результативного, связь обнаруживается в виде тенденции изменения среднего значения результативного в зависимости от изменения факторного признака. Является не полной: мы не знаем всех факторов и их воздействия.

5 Основные приемы изучения взаимосвязей метод сопоставления параллельных рядов, балансовый, графический, методы аналитических группировок, дисперсионного и корреляционного анализа.

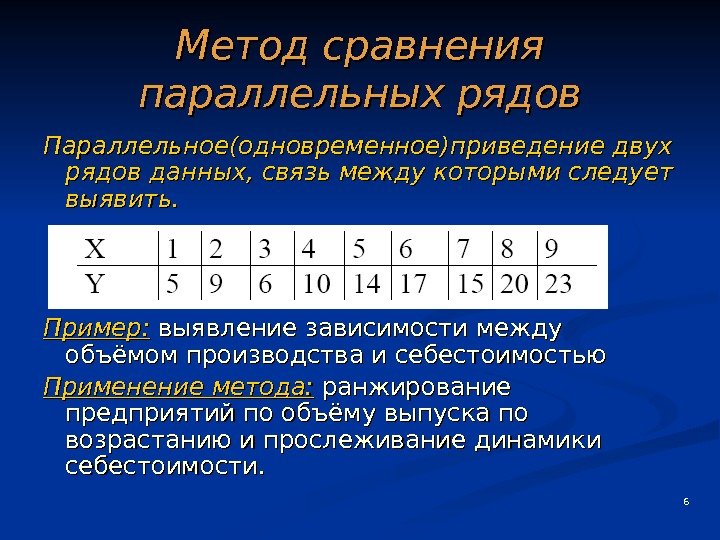
6 Метод сравнения параллельных рядов Параллельное(одновременное)приведение двух рядов данных, связь между которыми следует выявить. Пример: выявление зависимости между объёмом производства и себестоимостью Применение метода: ранжирование предприятий по объёму выпуска по возрастанию и прослеживание динамики себестоимости.

7 Балансовый метод Изображение данных взаимосвязанных показателей в виде таблицы и их расположение так, чтобы итоги между отдельными её частями были равны (сбалансированы). Используется для характеристики взаимосвязи между производством и распределением продуктов, денежными доходами и расходами населения.

8 Регионы отправле нияния Регионы прибытия Итого отправлено АА ББ ВВ ГГ АА 2525 7575 8080 100100 280280 ББ 100100 2020 9595 3030 245245 ВВ 8080 7070 3030 6565 245245 ГГ 7070 4545 5555 3535 205205 Итого прибыло

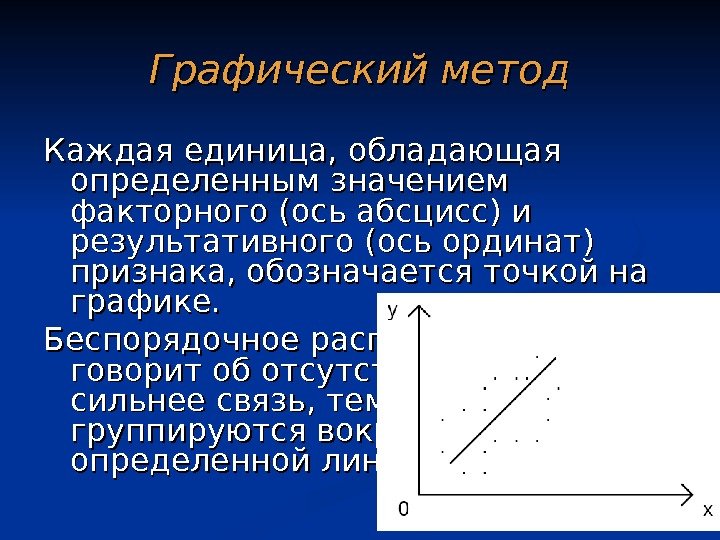
9 Графический метод Каждая единица, обладающая определенным значением факторного (ось абсцисс) и результативного (ось ординат) признака, обозначается точкой на графике. Беспорядочное расположение точек говорит об отсутствии связи. Чем сильнее связь, тем теснее точки группируются вокруг определенной линии.

10 Метод аналитической группировки 1. Группировка единиц совокупности по факторному признаку. 2. Расчёт средней или относительной величины по результативному признаку для каждой группы. 3. Сопоставление характера изменений значений факторного и результативного признака для выявления характера связи между ними.

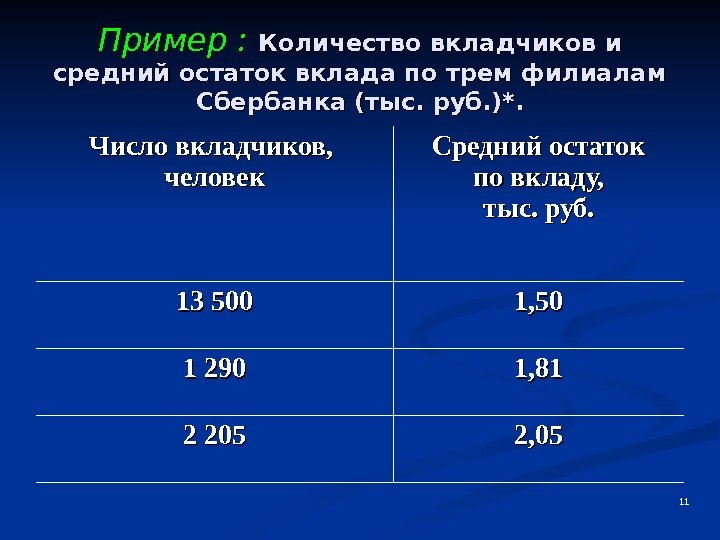
11 Пример : Количество вкладчиков и средний остаток вклада по трем филиалам Сбербанка (тыс. руб. )*. Число вкладчиков, человек Средний остаток по вкладу, тыс. руб. 13 5 00 00 1, 50 1 290 1, 81 2 205 2,

12 Дисперсионный анализ Дает возможность установить роль определенного фактора в изменении результативного признака. 1. 1. Определение вида признака- факторный/результативный 2. 2. Группировка по факторному признаку 3. 3. Расчёт среднего значения факторного и результативного признака в группах 4. 4. Выявление взаимосвязи между рассчитанными средними.

13 Для оценки тесноты связи по результатам факторной группировки используется эмпирическое корреляционное отношение (см. Т 4). Чем ближе корреляционное отношение к 1, тем большее влияние оказывает факторный признак на результативный. 1;

14 Дисперсионный анализ позволяет установить, вызвана ли межгрупповая вариация признаком, положенным в основание группировки, или она является результатом действия случайных причин. Для оценки существенности корреляционного отношения пользуются критическими значениями корреляционного отношения η η при разных уровнях вероятности или значимости αα. . Уровень значимости – это достаточно малое значение вероятности, отвечающее событиям, которые в данных условиях исследования будут считаться практически невозможными. Появление такого события считается указанием на неправильность начального предположения. Чаще всего пользуются уровнями, равными 0, 05 или 0, 01.

15 kk 11 = m – 11 , , где mm – число групп для случайной дисперсии kk 2 = n – m, где n n – число вариант, mm – число групп для факторной дисперсии

16 Критерий Фишера 22 : . 1 i F n n m Фишер составил таблицы, по которым можно определить значения критерия. Если мы получаем значение FF , большее, чем значение в таблице, то рассчитываемое значение получилось неслучайно (с вероятностью 99% или 95%, в зависимости от того, какую таблицу мы взяли). Критерий Фишера можно использовать только тогда, когда распределение близко к нормальному

173. 3. Корреляционно-регрессио нный анализ — задачи: определение формы связи (построение уравнения регрессии); измерение тесноты связи (расчет коэффициентов корреляции).

18 Этапы корреляционного анализа : : 1)1) предварительный анализ объекта исследования; 2)2) сбор и первичная обработка информации; 3)3) построение уравнения регрессии и определение его параметров; 4)4) проверка адекватности полученной модели.

19 Виды корреляционно-регрессионн ых связей 1. 1. По направлению: Прямая / / Обратная – 2. 2. По числу факторных признаков: Однофакторные (парная корреляция)/многофакторные 3. 3. По аналитическому выражению: Прямолинейная / криволинейная

204. Аналитическое выражение формы связи. Регрессионный анализ дает возможность выражать связь между признаками аналитически (в виде уравнения) и придавать ей количественное выражение. Регрессия (как и корреляция) может быть: Парная(характеризует связь между двумя признаками: результативным и факторным) Множественная (связь между тремя и более связанными между собой признаками)

21 Парная регрессия : : по по аналитическому выражению Прямолинейная зависимость (результат изменяется приблизительно равномерно в соответствии с изменением фактора) выражается уравнением прямой: аа 11 — — коэффициент регрессии — показывает, насколько в среднем отклоняется величина результативного признака y y при отклонении величины факторного признака xx на одну единицу. 0 1 , y a a x

22 Криволинейная — выражается уравнением криволинейной связи уравнение параболы второго порядка аа 22 — — параметр характеризует степень ускорения или замедления кривизны параболы гипербола

23 Параметры для всех уравнений связи, определяют из системы нормальных уравнений, которые должны отвечать требованию метода наименьших квадратов (МНК). Для нахождения параметров линейной парной регрессии система имеет вид: yxana 10 xyxaxa 2 10 где nn – объем исследуемой совокупности (число единиц наблюдения).

Нахождение параметров позволит определить теоретические значения Y для разных значений x i. Причём а 0 и а 1 должны быть такими , чтобы было достигнуто максимальное приближение к первоначальным значениям y теоретических значений Y

Множественная регрессия Линейная зависимость результативного признака от двух факторныхzaxaa. Y xz 210 xzaxaxayx zaxzaxayz zaxanay

265. Измерение тесноты связи Степень зависимости вариации результативного признака от вариации признака-фактора характеризуется одноименными показателями: параметрические непараметрические.

27 Вид показателя зависит от характера взаимосвязанных признаков: Признак-фа ктор Признак-ре зультат Показатель тесноты колич-й Линейный коэффициент парной корреляции несколько колич-х колич-й множественный коэффициент корреляции качест-й альтернат- й колич-й Биссериальный коэффициент корреляции качест-й альтернат- й Коэффициент ассоциации / контингенции качест-й варьирующ ий коэффициент взаимной сопряженности Пирсона-Чупрова Колич-й или качест-й ранжирова нный Ранговые коэффициенты корреляции

282 2 xy x y r 2 2 ( )( ). ( ) i i i xy i i x x y y r x x y y 1 1. xy r или 1. 1. связь прямолинейная 2. 2. один количественный фактор Линейный коэффициент корреляции — rr xyxy

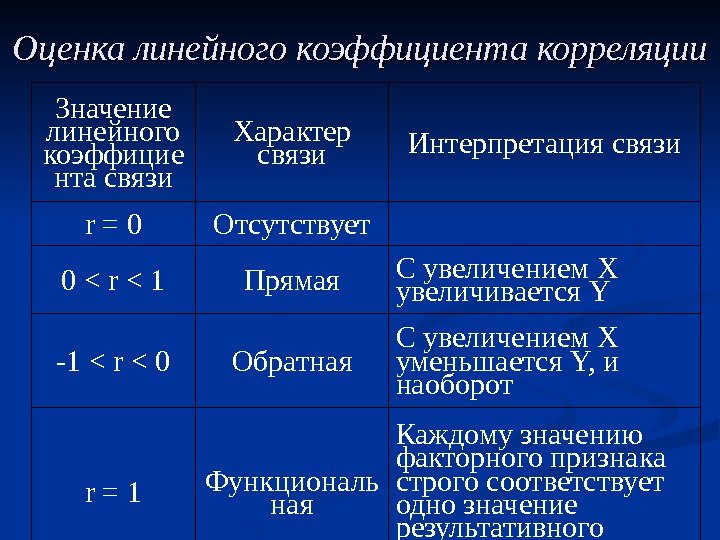
Оценка линейного коэффициента корреляции Значение линейного коэффицие нта связи Характер связи Интерпретация связи r = 0 Отсутствует 0 < r < 1 Прямая С увеличением X увеличивается Y -1 < r < 0 Обратная С увеличением X уменьшается Y, и наоборот r = 1 Функциональ ная Каждому значению факторного признака строго соответствует одно значение результативного признака

Количественные критерии оценки тесноты связи

31 Коэффициент множественной корреляции где rr xyxy , r, r zyzy , r, r xzxz – парные коэффициенты корреляции 2 2 ; , 2 2 , 1 yx yz xz y x z xz r r r R r 1. 1. связь прямолинейная 2. 2. два количественных фактора 10 , , zxy R

Частные коэффициенты корреляции 1. 1. связь прямолинейная 2. 2. один количественный фактор меняется, другой количественный фактор – зафиксирован как постоянное значение)1)(1( 22)( xzzyxy zxy rr r

33 Индекс корреляции 10 1. 1. связь любая (в том числе криволинейная) 2. 2. один количественный фактор 2 2 n yy x 2 2 )( n yy 2 2 )( δ 2 — дисперсия в ряду выровненных значений результативного показателя σ 2 — дисперсия в ряду фактических значений у xy

34 Коэффициент (индекс) детерминации 2 2 2 общ. T R Показывает, какая часть общей дисперсии результативного признака определяется факторами, включенными в уравнение регрессии. 1. 1. связь любая (в том числе криволинейная) 2. 2. несколько количественных факторов

351. 1. Фактор — качественный альтернативный признак 2. 2. Результат — аналогично Коэффициент ассоциации Д. Юла: / / контингенции К. Пирсона: bcad К а )()(dccadbba bcad Kk a b a+b c d c+d a+c b+d a+b+c+d

361. 1. Фактор — качественный варьирующий признак 2. 2. Результат — аналогично Коэффициент взаимной сопряженности К. Пирсона и А. Чупрова 2 2 1 п К )1)(1( 21 2 КК чк 1 2 2 yx xy nn n где φ 2 — показатель взаимной сопряженности К 1 — число значений (групп) первого признака; К 2 — число значений (групп) второго признака.

37 Коэффициент взаимной сопряженности К. Пирсона и А. Чупрова φ 2 = сумма отношений квадратов частот каждой клетки таблицы к произведению итоговых частот соответствующего столбца и строки минус 1:

381. 1. Фактор — качественный альтернативный признак 2. 2. Результат — количественный Биссериальный коэффициент корреляции где — средние в группах; σ y — СКО фактических значений признака от среднего уровня; p — доля первой группы; q — доля второй группы; Z — табулированные (табличные) значения Z -распределения в зависимости от p. 1 у2 у

391. 1. Фактор – количественный или качественный упорядоченный признак 2. 2. Результат — аналогично Ранговые коэффициенты: корреляции рангов Спирмена и Кендалла Коррелируются не сами значения показателей х и у , а только порядковые номера их мест, которые они занимают в каждом проранжированном ряду значений (в порядке возрастания или убывания их величин). Если значения признака имеют одинаковую количественную оценку (связные ранги), то ранг всех этих значений принимается равным средней арифметической от соответствующих номеров мест.

Коэффициент корреляции рангов Спирмена

Ранговый коэффициент корреляции Кендалла где n – число наблюдений; S = P + Q – сумма разностей между числом последовательностей и числом инверсий по второму признаку.