11. Дискретные цепи и сигналы
• Аналоговый сигнал – непрерывная или кусочно-непрерывная функция x(t) • Дискретный сигнал (ДС) – последовательность отсчетов функции x(t), взятой в определенные моменты времени: 0 Т, 1 Т, 2 Т, …, n. Т, где Т – интервал времени, через которые берутся отсчеты (интервал дискретизации)
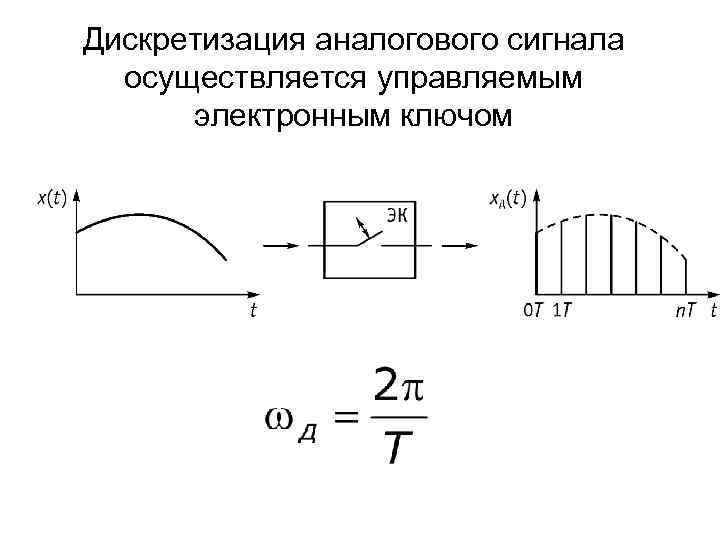Дискретизация аналогового сигнала осуществляется управляемым электронным ключом
Дискретный сигнал может быть представлен в виде: Теорема Котельникова во временной области Если функция x(t) имеет спектр, ограниченный некоторой частотой , то сигнал x(t) может быть полностью восстановлен по его отчетам, взятым через время
Связь между спектрами аналогового и дискретного сигналов
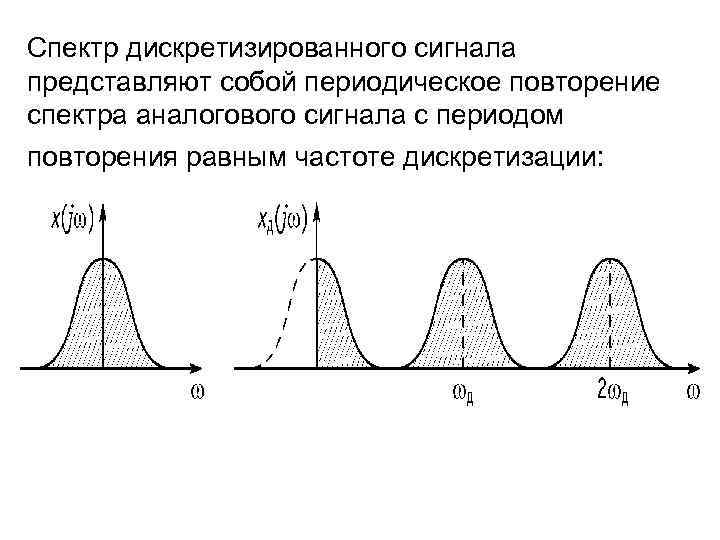Спектр дискретизированного сигнала представляют собой периодическое повторение спектра аналогового сигнала с периодом повторения равным частоте дискретизации:
Дискретное преобразований Фурье (ДПФ) для дискретизированного периодического сигнала, имеющего периодический дискретный спектр
Число отсчетов сигнала и число отсчетов его спектра одинаковы на периоде повторения
ДПФ применяют для периодических сигналов Огибающая спектра периодического дискретного сигнала совпадает со спектром дискретного непериодического сигнала. Можно определить спектр непериодического сигнала, используя ДПФ, для этого необходимо сделать его периодическим
Пример Применить прямое ДПФ к сигналу Делаем сигнал периодическим
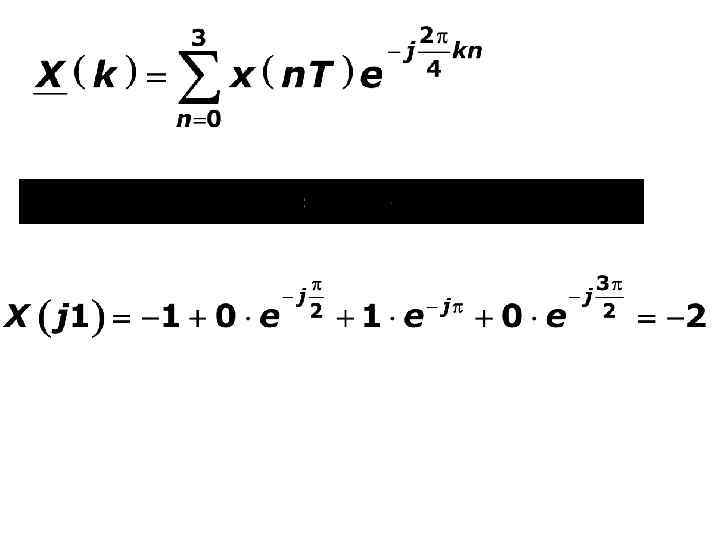
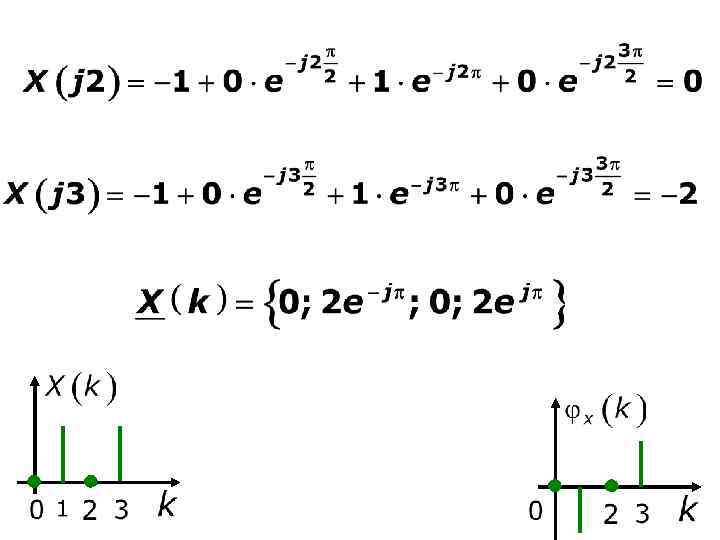
Z-преобразование дискретного сигнала
Если задан дискретный сигнал то его Z-изображение
По Z-изображению можно найти дискретный сигнал x(n. T): Пример
Дискретные цепи.
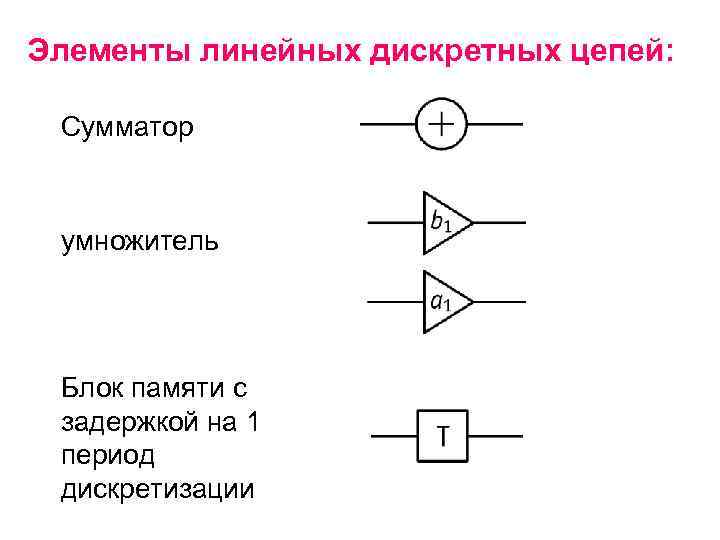Элементы линейных дискретных цепей: Сумматор умножитель Блок памяти с задержкой на 1 период дискретизации
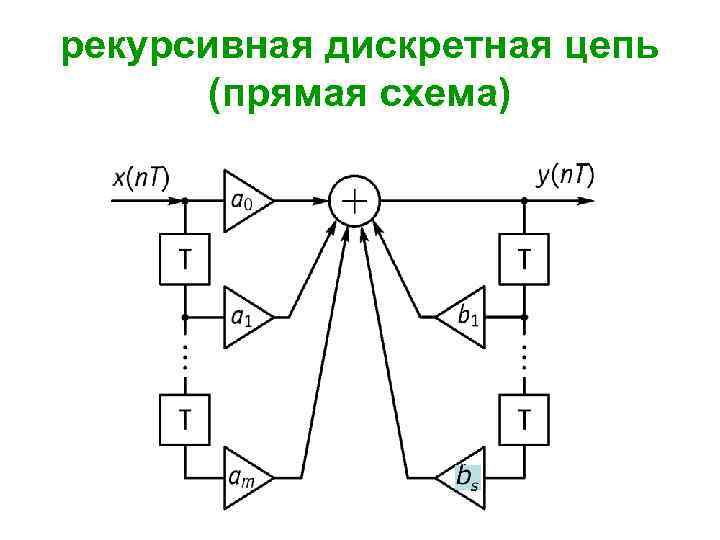рекурсивная дискретная цепь (прямая схема)
Разностное уравнение
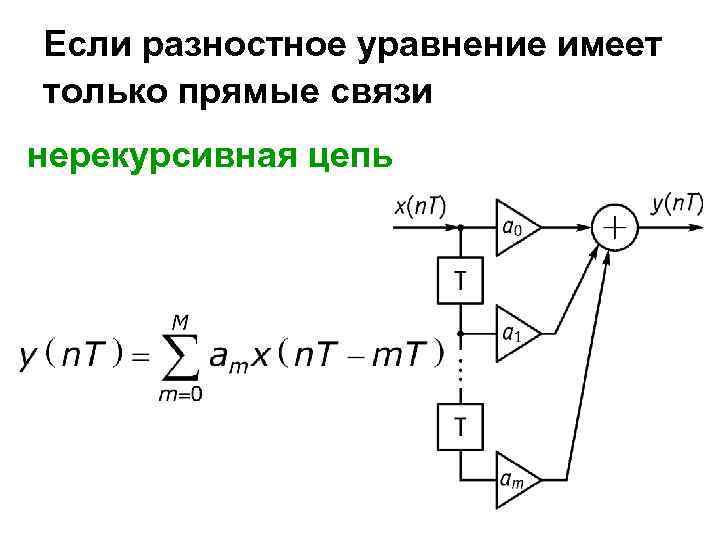Если разностное уравнение имеет только прямые связи нерекурсивная цепь
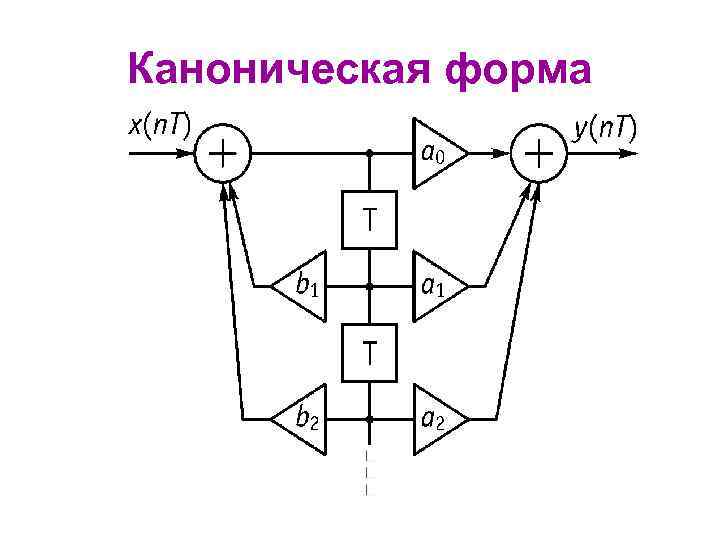Каноническая форма
Передаточная функция рекурсивной цепи нерекурсивной цепи Передаточная функция может быть получена путем Z-преобразования разностного уравнения
Устойчивость ДЦ Если полюсы передаточной функции цепи H(z) находятся внутри окружности единичного радиуса на комплексной плоскости z, то цепь устойчива
Комплексная частотная характеристика Частотные характеристики ДЦ – периодические функции с периодом, равным частоте дискретизации
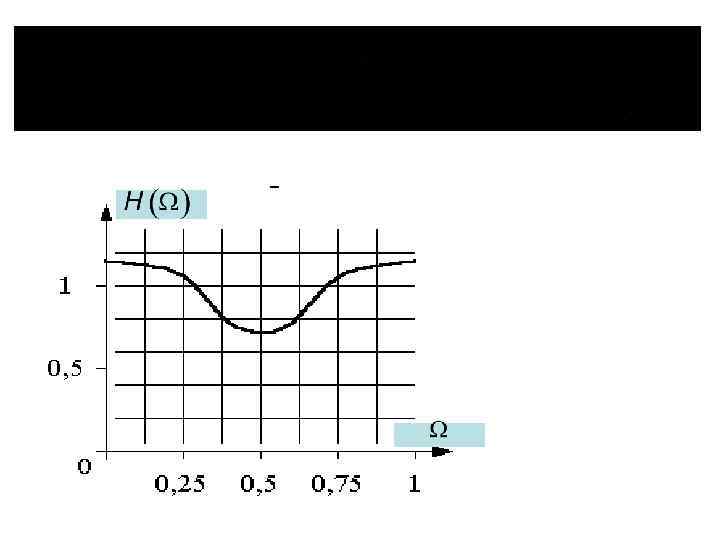
Пример рассчитать комплексную частотную характеристику
нормированная частота Достаточно рассчитать частотную характеристику в диапазоне
Импульсная характеристика дискретной цепи Импульсная характеристика цепи – реакция дискретной цепи на сигнал в виде δ-функции при
Способы определения импульсной характеристики 1. По разностному уравнению Пример
2. Выполнив обратное Z-преобразование H(z)
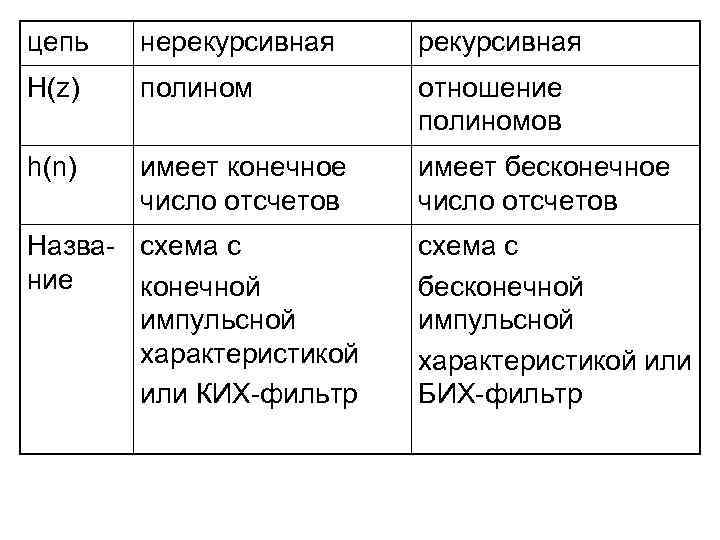цепь нерекурсивная H(z) полином отношение полиномов h(n) имеет конечное число отсчетов имеет бесконечное число отсчетов Назва- схема с ние конечной импульсной характеристикой или КИХ-фильтр схема с бесконечной импульсной характеристикой или БИХ-фильтр
Определение сигнала на выходе ДЦ 1) По разностному уравнению 2) С помощью линейной свертки Пример Выполнить линейную свертку входного сигнала импульсной характеристики и
Решение Определим длину выходной последовательности где - длина входной последовательности, - длина импульсной характеристики.
Найдем
