11 Динамическое программирование 1 2 3 4 5

11. Динамическое программирование 1. 2. 3. 4. 5. Общая характеристика задач динамического программирования. Геометрическая интерпретация. Экономическая интерпретация. Особенности задач динамического программирования. Специфика метода динамического программирования.

1. Общая характеристика задач динамического программирования В рассмотренных выше задачах линейного и нелинейного программирования мы находили их решение как бы в один этап или за один шаг (этап) – одношаговые (одноэтапные) задачи. Однако многие задачи планирования и управления являются, как правило, многоэтапного выбора (принятия решений), то есть процесс управления рассматривается во времени. Такие задачи относятся к классу задач динамического программирования. n Пусть состояние системы в начальный момент времени S 0 характеризуется определенным набором ее параметров. Процесс управления системой заключается в выборе управляющих воздействий Ui на систему в определенные моменты времени i=1, 2, …, m, чтобы критерий эффективности системы W(U) был оптимален. n

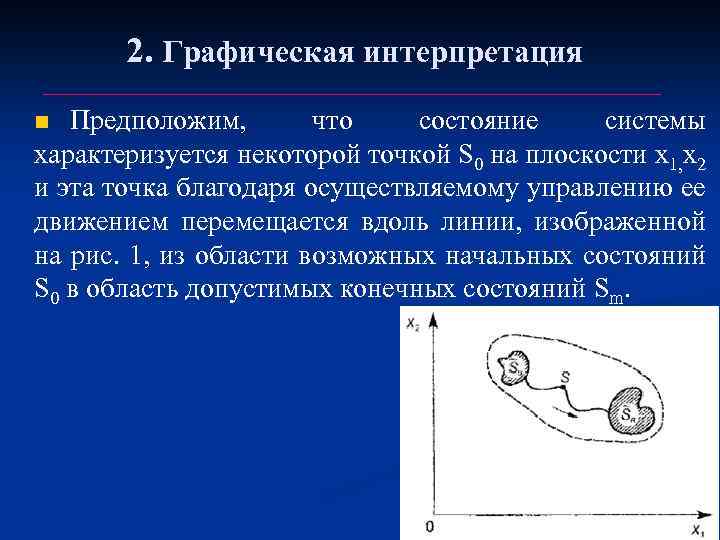2. Графическая интерпретация Предположим, что состояние системы характеризуется некоторой точкой S 0 на плоскости х1, х2 и эта точка благодаря осуществляемому управлению ее движением перемещается вдоль линии, изображенной на рис. 1, из области возможных начальных состояний S 0 в область допустимых конечных состояний Sm. n

Графическая интерпретация Каждому управлению U движением точки, то есть каждой траектории движения точки, соответствует значение некоторого критерия W(U) (например, длину пути, пройденного точкой под воздействием данного управления). Тогда задача состоит в том, чтобы из всех допустимых траекторий движения точки S найти такую, которая получается в результате реализации управления U*, обеспечивающего экстремальное значение функции W(U*). К определению такой «траектории» сводится и задача динамического программирования в случае, когда допустимые состояния системы S определяются точками п-мерного пространства. n

3. Экономическая интерпретация В распоряжение холдинга, в подчинении которого находится k предприятий, выделены средства в размере R у. е. для использования их на развитие предприятий в течение m лет. Эти средства в начале каждого хозяйственного года, то есть в моменты t 1, t 2, . . . , tm, распределяются между предприятиями. Одновременно с этим между предприятиями распределяется полученная ими за прошедший год прибыль. Таким образом, в начале каждого i-го года рассматриваемого периода j-е предприятие получает в свое распоряжение xi(j) у. е. n Определить такие значения xi(j), то есть найти такие распределения выделенных средств и получаемой прибыли между предприятиями, при которых за m лет обеспечивается получение максимальной прибыли всеми предприятиями. n

Экономическая интерпретация n В данной задаче распределение средств есть реализация некоторого управления ui, которое состоит в том, что на і-м шаге первому предприятию выделяется xi(1) у. е. , второму – xi(2) у. е. и т. д. Совокупность чисел xi(1), xi(2), …, xi(k) определяет всю совокупность управлений u 1, u 2, . . . , um на m шагах распределения средств как m точек в k-мерном пространстве. n Критерием оценки качества выбранного распределения средств, то есть реализуемых управлений, взята суммарная прибыль за m лет, которая зависит от всей совокупности управлений: W = W(u 1, u 2, …, um). Следовательно, задача состоит в выборе таких управлений U* (то есть в таком распределении средств) при которых функция W принимает максимальное значение. n Как видно, сформулированная задача является многоэтапной. Эта многоэтапность диктуется ее условиями, предусматривающими принятие определенных решений в начале каждого года рассматриваемого периода.

4. Особенности задач динамического программирования В них рассматривается процесс поведения системы во времени. n Состояние системы в каждый момент времени однозначно определяется численными значениями набора параметров. n Операция выбора решения состоит в преобразовании этого набора параметров в такой же набор с другими числовыми значениями. n Если система в рассматриваемый момент времени находится в некотором состоянии, то ее поведение в дальнейшем определяется этим состоянием и выбираемым управлением, но не зависит от предыстории, т. е. от того, в каких состояниях находилась система до этого момента (условие отсутствия последействия). n

5. Специфика метода динамического программирования состоит в том, что для отыскания оптимального управления изучаемый процесс расчленен на этапы. Он представляется как развивающийся по этапам, причем каждый раз оптимизируется управлением только на одном этапе. n Будем считать, что состояние рассматриваемой системы S на i -м шаге (i=1, 2, …, m) определяется совокупностью чисел ее параметров (Х(i) = х1(i), х2(i), …, xn(i)), которые получены в результате реализации управления ui, обеспечившего переход системы S из состояния Х(i-1) в состояние Х(i). При этом полагаем, что состояние Х(i), в которое перешла система зависит от данного состояния Х(i-1) и выбранного управления ui и не зависит от того, каким образом система в пришла в состояние Х(i-1). n

Специфика метода динамического программирования Условимся, что в результате реализации i-то шага обеспечен определенный доход или выигрыш, также зависящий от исходного состояния системы Х(i-1) и выбранного управления ui равный W(X(i-1), ui), и общий доход или выигрыш за m шагов составляет как сумма выигрышей на каждом шаге n n F = Wi(X(i-1), ui) (11. 1) Если критерий F обладает этим свойством, то он называется аддитивным. n Таким образом, под оптимальной стратегией управления понимается совокупность управлений U* = (u 1*, u 2*, …, um*) в результате реализации которых система S за m шагов переходит из начального состояния Х(0) в конечное Х(m) и при этом функция (11. 1) принимает наибольшее значение. n

Специфика метода динамического программирования Каково бы ни было состояние системы перед очередным шагом, надо выбрать управление на этом шаге так, чтобы выигрыш на данном шаге плюс оптимальный выигрыш на всех последующих шагах был максимальным. n Отсюда следует, что оптимальную стратегию управления можно получить, если сначала найти оптимальную стратегию управления на m-ом шаге, затем на двух последних шагах, затем на трех последних шагах и т. д. , вплоть до первого шага. n При этом решение рассматриваемой задачи динамического программирования целесообразно начинать с определения оптимального решения на последнем, m-м шаге. Для того чтобы найти это решение, очевидно, нужно сделать различные предположения о том, как мог окончиться предпоследний шаг, и с учетом этого выбрать управление um*, обеспечивающее максимальное значение функции Wm(X(m-1), um). n

Специфика метода динамического программирования Такое управление um* выбранное при определенных предположениях о том, как окончился предыдущий шаг, называется условно оптимальным управлением. Следовательно, принцип оптимальности требует находить на каждом шаге условно оптимальное управление для любого из возможных исходов предшествующего шага. n Чтобы это можно было осуществить практически, необходимо дать математическую формулировку принципа оптимальности. Для этого введем некоторые дополнительные обозначения. Обозначим через Fm(X(0)) максимальный доход, получаемый за m шагов при переходе системы S из начального состояния Х(0) в конечное состояние Х(m) при реализации оптимальной стратегии управления U* = (u 1*, u 2*, . . . , um*), а через Fm-i(X(i)) – максимальный доход, получаемый при переходе из любого состояния Х(i) в конечное состояние Х(m) при оптимальной стратегии управления на оставшихся m-i шагах. n

Специфика метода динамического программирования Тогда Fm(X(0)) = mах[W 1(Х(0), u 1) + W 2(Х(1), u 2)+, . . . , + Wm(Х(m-1), um))]. n Исходя из условия отсутствия последействия, получаем функцию Fm-i(X(i)) = mах[Wi-1(Х(i), ui-1) + Fm-i+1(Х(i+1))] n Последнее выражение представляет собой математическую запись принципа оптимальности и носит название основного функционального уравнения Беллмана, которое обеспечивает нахождение решения рассматриваемой задачи динамического программирования. n