11 Annuities Ordinary Chapter 11 Mc Graw-Hill Ryerson

11 Annuities Ordinary Chapter 11 Mc. Graw-Hill Ryerson© 1

Learning Objectives 11 After completing this chapter, you will be able to: LO-1 Calculate the… … payment size in ordinary and deferred annuities LO-2 … number of payments in ordinary and deferred annuities LO-3 … interest rate in ordinary annuities Mc. Graw-Hill Ryerson© 2

3 11 Using your financial calculator … solve for payment number or size or interest rate using the same steps as before … we need to reorganize the formulae to solve algebraically Mc. Graw-Hill Ryerson©

4 11 Finding the Payment Size…. PMT Mc. Graw-Hill Ryerson©

Finding Payment Size 11 5 of an Ordinary Simple Annuity Your life partner somehow convinced you that you can’t afford the car of your dreams, priced at $28800. You are advised to… “Save up for 4 years and then buy the car for cash. ” How much would you have to save each month, if PMT you could invest with a return of 10% compounded monthly? You need to decide if this situation involves … a PV or a FV and then use the appropriate formula. . . As you have to save up the $28, 800, i. e. in the future, FV = $28, 800 Assume you have no savings … PV = 0 Mc. Graw-Hill Ryerson©

11 Finding Payment Size of an Ordinary Simple Annuity Your life partner somehow convinced you that you can’t afford the car of your dreams, priced at $28800. (At least not right now). You are advised to… “Save up for 4 years and then buy the car for cash. ” How much would you have to save each month, if you could invest with a return of 10% compounded monthly? Mc. Graw-Hill Ryerson© PMT = - 490. 44 12 10 28800 0 48 Formula solution 6

11 7 Which Formula? Algebraic Method of Solving for PMT PV = PMT [ ] 1 -(1+ i)-n i [ n FV = PMT (1+ i) - 1 i 1. (a) If the payments form a Simple Annuity go directly to 2. (b) If the payments form a General Annuity, find c and i 2 2. If the annuity’s PV is known, substitute values of PV, n, and i into PV formula. If the annuity’s FV is known, substitute values of FV, n, and i into FV formula. 3. Mc. Graw-Hill Ryerson© & 4. ]

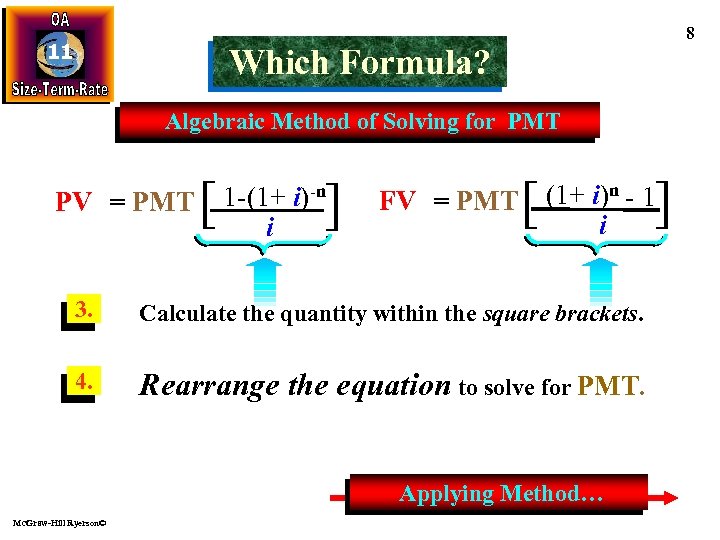11 8 Which Formula? Algebraic Method of Solving for PMT PV = PMT [ ] 1 -(1+ i)-n i [ 3. Calculate the quantity within the square brackets. 4. Rearrange the equation to solve for PMT. Applying Method… Mc. Graw-Hill Ryerson© ] (1+ i)n - 1 FV = PMT i

11 9 Finding Payment Size of an Ordinary Simple Annuity Which Formula? Your life partner 2. As the annuity’s FV is known, somehow convinced you that you can’t afford therefore, the FV formula is used car of your dreams, priced at $28800. (At least (1+ i)n - 1 not right now). You are FV = PMT advised to… i “Save up for 4 years and Extract necessary data. . . then buy the car for cash. ” How much would you FV = 28800 PV = 0 n = 4*12 = 48 have to save each month, i =. 10/12 c = 1 PMT = ? if you could invest with a return of 10% compounded monthly? [ Mc. Graw-Hill Ryerson© ]

11 Your life partner somehow convinced you that you can’t afford the car of your dreams, priced at $28800. (At least not right now). You are. 10 advised to… “Save up for 4 years and then buy the car for cash. ” How much would you have to save each month, if you could invest with a return of 10% compounded monthly? Mc. Graw-Hill Ryerson© [ Formula FV = PMT (1+ i)n - 1 i FV = 28800 PV = 0 n = 4*12 = 48 i =. 10/12 c = 1 PMT = ? ] 58. 7225 490. 44 0. 4894 1. 0083 0. 0083 12 1 48 1 28800 …another example 10

11 11 The Mc. Graw-Hill Ryerson©

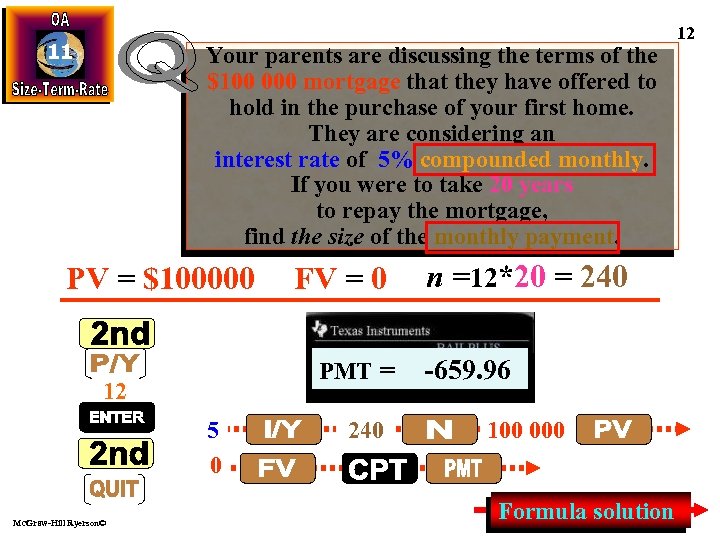11 Your parents are discussing the terms of the $100 000 mortgage that they have offered to hold in the purchase of your first home. They are considering an interest rate of 5% compounded monthly. If you were to take 20 years to repay the mortgage, find the size of the monthly payment. PV = $100000 PMT = 12 5 0 Mc. Graw-Hill Ryerson© FV = 0 240 n =12*20 = 240 -659. 96 100 000 Formula solution 12

11 Your parents are discussing the terms of the 100 000 mortgage that they have offered to hold in the purchase of your first home. They are considering an interest rate of 5% compounded monthly. If you were to take 20 years to repay the mortgage, find the size of the monthly payment. Mc. Graw-Hill Ryerson© 13 Extract necessary data. . . PV = $100000 i =. 05/12 n =12*20 = 240 FV = 0 C =1

14 11 Choose appropriate formula and Solve 2. As the annuity’s PV is known, the PV formula is used [ ] Formula PV = PMT 1 -(1+ i)-n n =12*20 =240 PV = $100000 i =. 05/12 -0. 6314 659. 96 0. 0015 151. 53 0. 3686 1. 0042 0. 0042 12 . 05 240 Size of monthly mortgage payment 1 1 100 000 Mc. Graw-Hill Ryerson© i

11 15 How much interest will you pay your parents over the 20 year period? Amount $ Monthly Payment x Number of Payments 659. 96 240 158, 390. 40 Amount Borrowed Total Interest Paid Mc. Graw-Hill Ryerson© 100, 000. 00 58, 390. 40

16 11 As this amount of interest shocks you, you discuss the possibility of making payments of $700/month, to save some time and interest costs. Determine the time it will take you to repay your mortgage at this new rate. Mc. Graw-Hill Ryerson© N= PMT = 217. 52 -700 218 payments = 18 yrs 2 months Formula solution

11 Formula n 0 i =. 05/12 [ ] PV * i PMT ln 1 n ln (1+ i) PV = $100, 000 PMT = $700 C = 1 -0. 9045 -0. 4048 0. 5952 1. 0042 0. 0042 -217. 52 12 . 05 1 100 000 700 1 218 payments = 18 yrs 2 months Mc. Graw-Hill Ryerson© 17

11 Formula [ ln 1 n PV * i PMT ] 18 ln (1+ i) Developing the Formula 1. Base formula 2. To isolate n, divide both sides by PMT [ [ PV = PMT PMT PV = PMT [ ] ] 1 - (1+ i)-n i …Continue… Mc. Graw-Hill Ryerson©

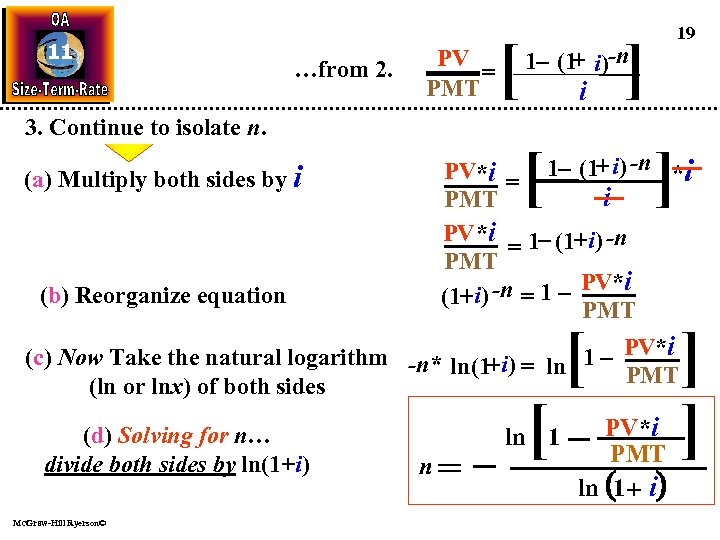11 …from 2. 3. Continue to isolate n. (a) Multiply both sides by i (b) Reorganize equation PV = PMT [ 19 ] 1 - (1+ i)-n i [ ] [ [[ ] i i] PV*i = 1 - (1+ i) -n *i i PMT PV *i 1 - (1+ i) -n = PMT + i) -n = 1 - PV*i (1 PMT (c) Now Take the natural logarithm -n* ln (1+ i) = ln 1 - PV*i PMT (ln or lnx) of both sides (d) Solving for n… divide both sides by ln(1+i) Mc. Graw-Hill Ryerson© PV* * ln= ln 1 - PV 1 -n* ln(1+ i) PMT n ln (ln(1+i) 1 + i) ln(1+i)

20 11 Approximately how much money do you save in interest charges by paying $700/month, rather than $659. 91/month? Amount $ Monthly Payment x Number of Payments 659. 96 240 158, 390. 40 700. 00 217. 52 Total Interest Saved Mc. Graw-Hill Ryerson© 152, 264. 00 6, 126. 40

21 11 If you could see your way to a further increase of $25/month, (a) how much faster would you pay off the mortgage, and (b) approximately how much less interest would be involved? N= PMT = 205. 62 -725 Paying $725 206 payments = 17 yrs 2 months Formula solution Mc. Graw-Hill Ryerson©

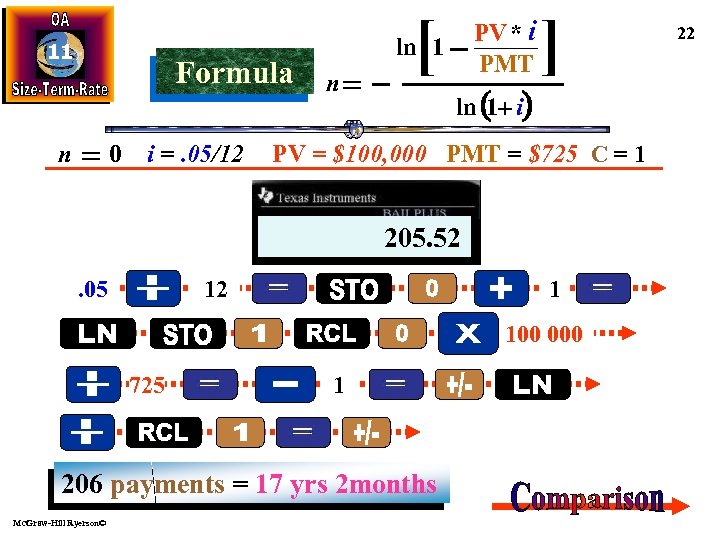11 Formula n 0 i =. 05/12 [ PV * i PMT ln 1 n ] ln (1+ i) PV = $100, 000 PMT = $725 C = 1 -205. 52 -0. 8550 -0. 4253 205. 52 1. 0042 0. 5747 12 . 05 1 100 000 725 1 206 payments = 17 yrs 2 months Mc. Graw-Hill Ryerson© 22

23 11 Amount $ Monthly Payment x Number of Payments 700. 00 217. 52 or 218 152, 264. 00 725. 00 205. 62 or 206 149, 074. 50 12 (a) Payments Saved (b)Total Interest Saved 3, 189. 50 Mc. Graw-Hill Ryerson©

11 Mc. Graw-Hill Ryerson© 24

Finding Payment Size 11 in a Deferred Annuity York Furniture has a promotion on a bedroom set selling for $2250. Buyers will pay “no money down and no payments for 12 months. ” The first of 24 equal monthly payments is due DEFERRAL 12 months from the purchase date. What should the monthly payments be if York Furniture PMT earns 10% compounded monthly on its account receivable during both the deferral period and the repayment period? Since you want the furniture now, this involves a PV PV = $2250 Once you repay the loan, FV = 0 Payments are deferred for 11 months. Mc. Graw-Hill Ryerson© 25

York Furniture has a promotion on a bedroom set selling for $2250. Buyers will pay “no money down and no payments for 12 months. ” The first of 24 equal monthly payments is due 12 months from the purchase date. What should the monthly payments be if York Furniture earns 10% compounded monthly on its account receivable during both the deferral period and the repayment period? 11 In effect, York furniture has given a loan to a buyer of $2, 250 on the day of the sale! When the payments begin, the buyer owes $2, 250 plus accrued interest! Mc. Graw-Hill Ryerson© 26

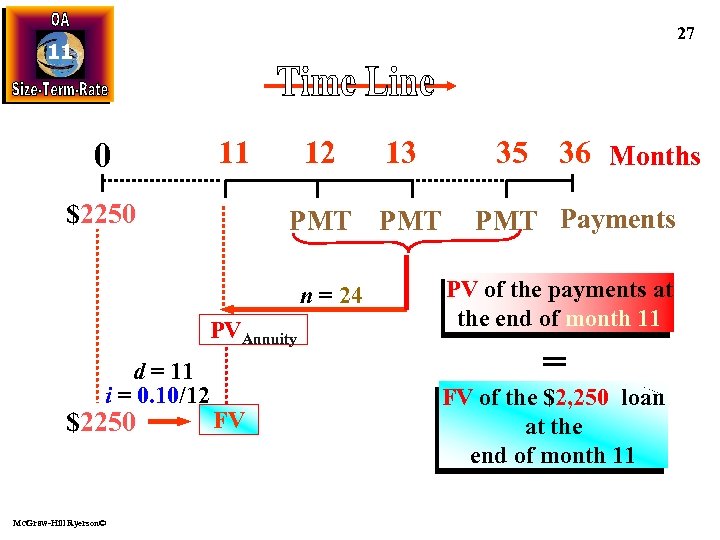27 11 11 0 $2250 12 PMT n = 24 PVAnnuity d = 11 i = 0. 10/12 $2250 Mc. Graw-Hill Ryerson© 35 36 Months 13 FV PMT Payments PV of the payments at the end of month 11 = FV of the $2, 250 loan at the end of month 11

11 Finding Payment Size 28 in a Deferred Annuity York Furniture has a promotion on a bedroom set selling for $2250. Buyers will pay “no money down and no payments for 12 months. ” The first of 24 equal monthly payments is due 12 months from the purchase date. What should the monthly payments be if York Furniture earns 10% compounded monthly on its account receivable during both the deferral period and the repayment period? Mc. Graw-Hill Ryerson© Find the amount owed after 11 months: FV = 2, 465. 06 10 0 11 12 2250 $2, 465. 06 is the PV of the annuity

11 Finding Payment Size 29 in a Deferred Annuity York Furniture has a promotion on a bedroom set selling for $2250. Buyers will pay “no money down and no payments for 12 months. ” The first of 24 equal monthly payments is due 12 months from the purchase date. What should the monthly payments be if York Furniture earns 10% compounded monthly on its account receivable during both the deferral period and the repayment period? Mc. Graw-Hill Ryerson© Now find the PMT of the annuity … PMT =2, 465. 06 113. 75 PV FV = - 2, 465. 06 24 0 24 monthly payments of $113. 75 will repay the loan. Formula solution

11 Finding Payment Size 30 in a Deferred Annuity York Furniture has a promotion on a bedroom set selling for $2250. Buyers will pay “no money down and no payments for 12 months. ” The first of 24 equal monthly payments is due 12 months from the purchase date. What should the monthly payments be if York Furniture earns 10% compounded monthly on its account receivable during both the deferral period and the repayment period? Mc. Graw-Hill Ryerson© Find the amount owed after 11 months: Formula FV = PV(1 + i)n FV = 2250(1 + 0. 10/12)11 = $2, 465. 06 [ PV = PMT ] 1 - (1+ i)-n i 2465. 06 = PMT [1 -(1+. 10/12)-24]. 10/12 PMT = $113. 75 24 monthly payments of $113. 75 will repay the loan.

31 11 i. e. . Number Of Payments Mc. Graw-Hill Ryerson©

11 Finding Number Of Payments in a Deferred Annuity $20, 000 is invested in a fund earning 8% compounded quarterly. The first quarterly withdrawal of $1, 000 will be taken from the fund DEFERRAL five years from now. How many. N withdrawals will it take to deplete the fund? The FV of $20, 000 after the deferral, becomes the PV of the annuity. . . Payments are deferred for 19 quarters Mc. Graw-Hill Ryerson© 32

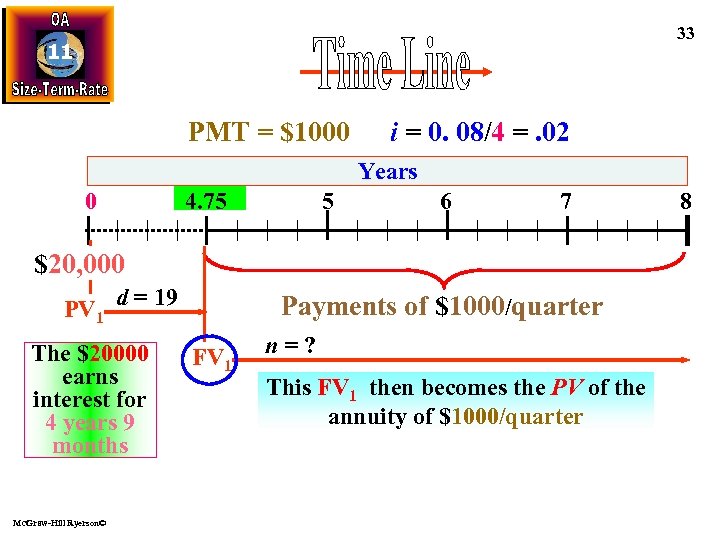33 11 PMT = $1000 i = 0. 08/4 =. 02 Years 0 4. 75 5 6 7 $20, 000 PV 1 d = 19 The $20000 earns interest for 4 years 9 months Mc. Graw-Hill Ryerson© Payments of $1000/quarter FV 1 n=? This FV 1 then becomes the PV of the annuity of $1000/quarter 8

11 Finding Number Of Payments in a Deferred Annuity $20, 000 is invested in a fund earning 8% compounded quarterly. The first quarterly withdrawal of $1000 will be taken from the fund five years from now. How many withdrawals will it take to deplete the fund? Mc. Graw-Hill Ryerson© Find the FV of $20, 000 in 4. 75 years FV = 29, 136. 22 4 8 0 19 20000 $29, 136. 22 is the PV of the annuity 34

11 Finding Number Of Payments 35 in a Deferred Annuity $20, 000 is invested Now find the PMT of the annuity … in a fund earning 8% compounded quarterly. N PV = 29136. 22 FV= - 29, 136. 22 44. 1 The first quarterly withdrawal of $1000 will be 1000 29136. 22 taken from the fund five years 0 from now. How many 44. 1 quarterly payments will deplete the withdrawals fund(44 full payments and 1 partial) will it take to deplete the fund? Formula solution Mc. Graw-Hill Ryerson©

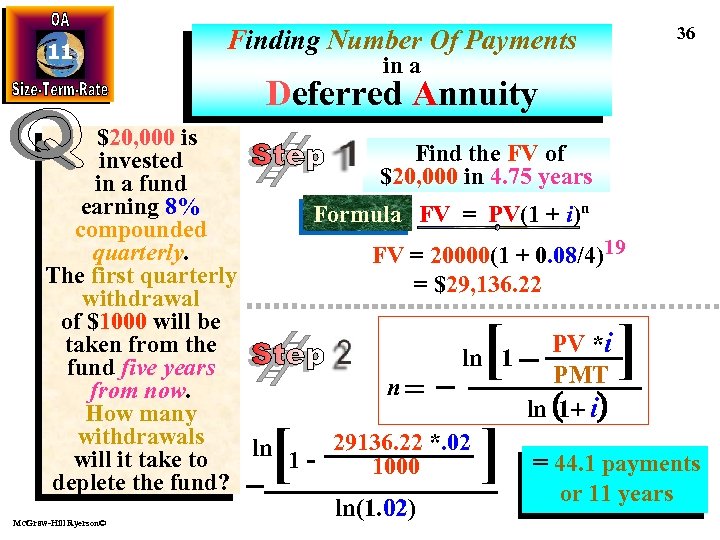11 36 Finding Number Of Payments in a Deferred Annuity $20, 000 is Find the FV of invested $20, 000 in 4. 75 years in a fund earning 8% Formula FV = PV(1 + i)n compounded quarterly. FV = 20000(1 + 0. 08/4)19 The first quarterly = $29, 136. 22 withdrawal of $1000 will be taken from the PV *i ln 1 fund five years PMT n from now. ln (1+ i) How many withdrawals ln 1 - 29136. 22 *. 02 will it take to = 44. 1 payments 1000 deplete the fund? or 11 years ln(1. 02) [ [ Mc. Graw-Hill Ryerson© ] ]

37 11 When… number of compoundings per year number of payments per year Mc. Graw-Hill Ryerson©

38 11 Since you get paid every second Thursday you decide to pay $350 every two weeks to make your budgeting easier. Find the new term of your mortgage if the interest charges remain at 5% compounded monthly. Mc. Graw-Hill Ryerson© C/Y= = 414. 74 N= 12 PMT P/Y = -350 26 26 12 350 415 bi-weekly payments or 15 yrs 11. 4 months Formula solution

11 Since you get paid every second Thursday you decide to pay $350 every two weeks to make your budgeting easier. Find the new term of your mortgage if the interest charges remain at 5% compounded monthly. Mc. Graw-Hill Ryerson© 39 Step 1 Determine c number of compoundings per year C = number of payments per year C= 12 / 26 =. 4615 Step 2 Use c to determine i 2 = (1+i)c - 1 i 2 = (1+. 05/12). 4615 -1 i 2 = 0. 0019 Step 3

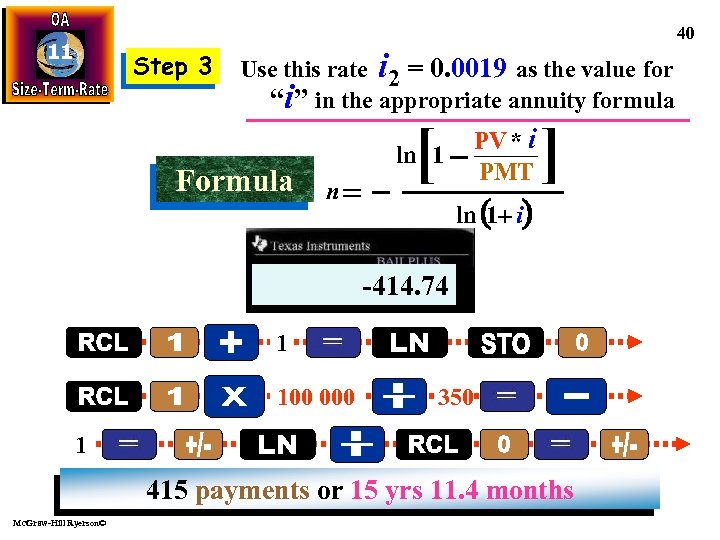40 11 Step 3 Use this rate i 2 = 0. 0019 as the value for “i” in the appropriate annuity formula Formula [ ln 1 n PV * i PMT ] ln (1+ i) -414. 74 -0. 7828 -0. 4571 0. 5428 0. 0019 1 100 000 350 1 415 payments or 15 yrs 11. 4 months Mc. Graw-Hill Ryerson©

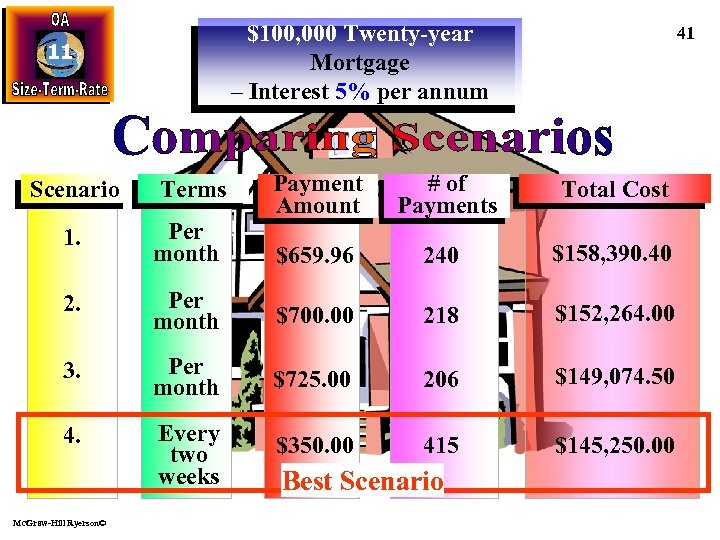$100, 000 Twenty-year Mortgage – Interest 5% per annum 11 Scenario Terms 41 Payment Amount # of Payments Total Cost $659. 96 240 $158, 390. 40 1. Per month 2. Per month $700. 00 218 $152, 264. 00 3. Per month $725. 00 206 $149, 074. 50 4. Every two weeks $350. 00 415 $145, 250. 00 Mc. Graw-Hill Ryerson© Best Scenario

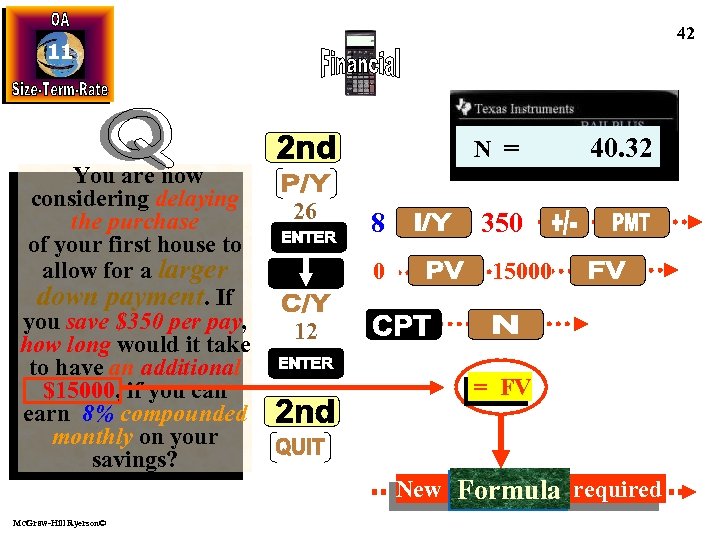42 11 You are now considering delaying the purchase of your first house to allow for a larger down payment. If you save $350 per pay, how long would it take to have an additional $15000, if you can earn 8% compounded monthly on your savings? N = 26 8 0 40. 32 350 15000 12 = FV New Formula required Mc. Graw-Hill Ryerson©

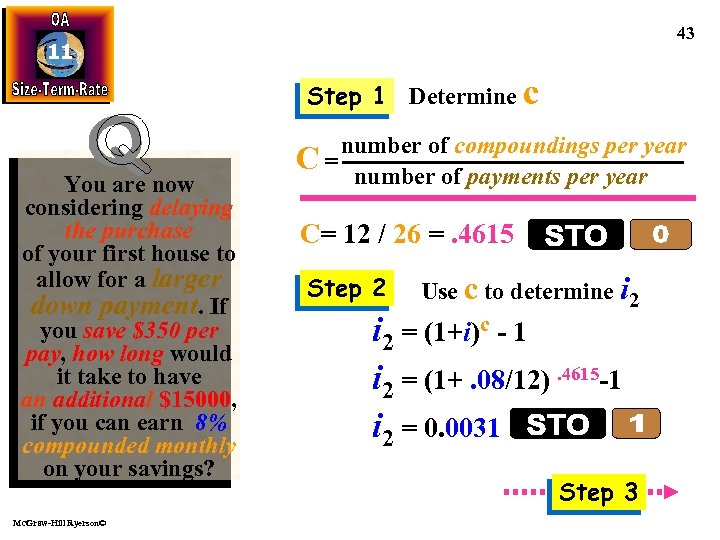43 11 Step 1 Determine c You are now considering delaying the purchase of your first house to allow for a larger down payment. If you save $350 per pay, how long would it take to have an additional $15000, if you can earn 8% compounded monthly on your savings? Mc. Graw-Hill Ryerson© number of compoundings per year C = number of payments per year C= 12 / 26 =. 4615 Step 2 Use c to determine i 2 = (1+i)c - 1 i 2 = (1+. 08/12). 4615 -1 i 2 = 0. 0031 Step 3

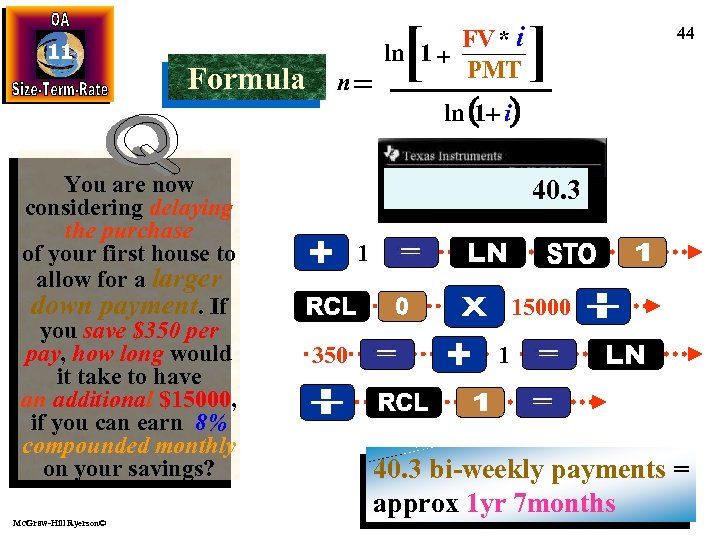11 Formula You are now considering delaying the purchase of your first house to allow for a larger down payment. If you save $350 per pay, how long would it take to have an additional $15000, if you can earn 8% compounded monthly on your savings? Mc. Graw-Hill Ryerson© [ FV * i ln 1 + PMT n ] 44 ln (1+ i) 0. 1316 0. 1237 1. 1316 0. 0031 1. 0031 40. 3 1 15000 350 1 40. 3 bi-weekly payments = approx 1 yr 7 months

11 Formula n [ FV * i ln 1 + PMT ] 45 ln (1+ i) Developing the Formula 1. Base formula 2. To isolate n, divide both sides by PMT [ [ FV = PMT PMT FV = PMT [ (1+ i) n - 1 i ] ] ] …continued… Mc. Graw-Hill Ryerson©

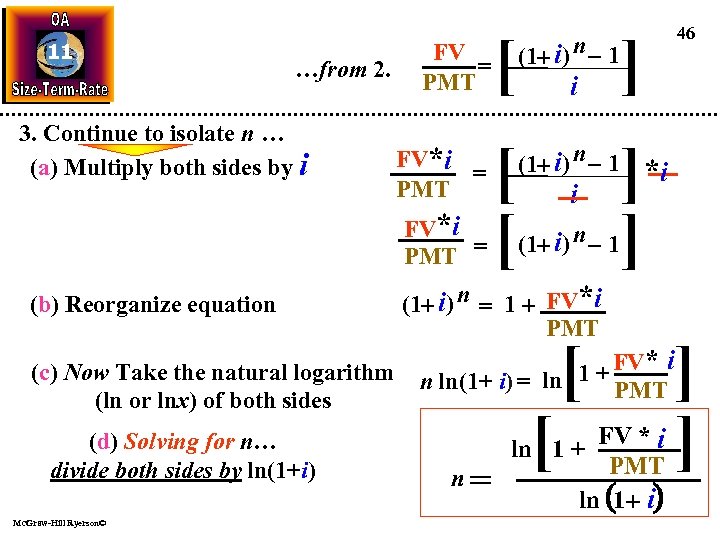11 …from 2. 3. Continue to isolate n … (a) Multiply both sides by i FV = PMT FV*i = PMT (b) Reorganize equation (c) Now Take the natural logarithm (ln or lnx) of both sides (d) Solving for n… divide both sides by ln(1+i) Mc. Graw-Hill Ryerson© [ (1+ i) n - 1 [ [ (1+ i) n - 1 i i (1+ i) n - 1 (1+ i) n = 1 + FV*i PMT [ [[ 46 ] ] *i ] ] ] 1 + FV * i n ln(1+ i) = ln PMT 1 + FV *i i = 1 n ln(1+ i)ln ln + FV * PMT n ln(1+i) ln (1 + i)

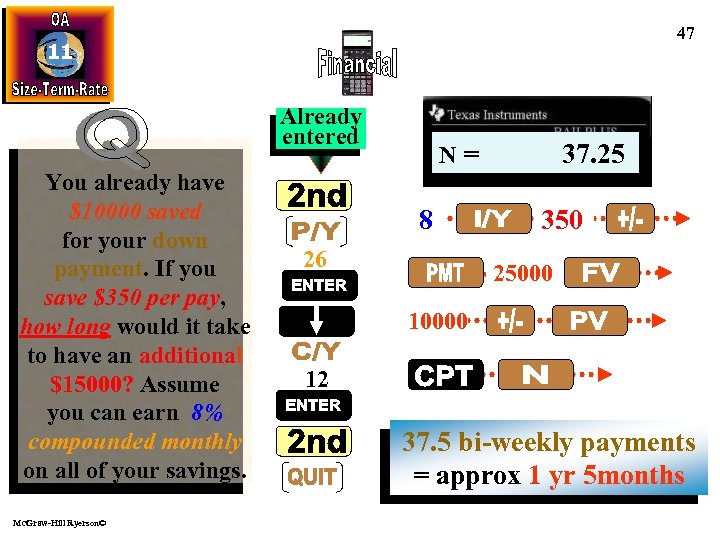47 11 Already entered You already have $10000 saved for your down payment. If you save $350 per pay, how long would it take to have an additional $15000? Assume you can earn 8% compounded monthly on all of your savings. Mc. Graw-Hill Ryerson© N= 8 26 37. 25 350 25000 10000 12 37. 5 bi-weekly payments = approx 1 yr 5 months

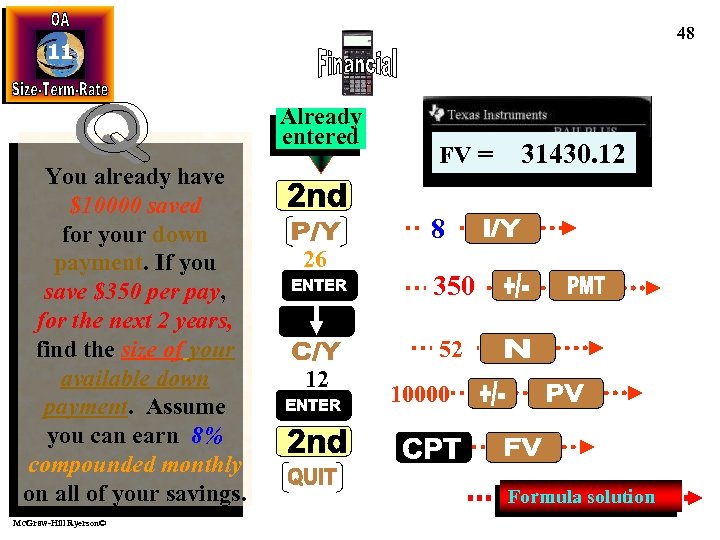48 11 Already entered You already have $10000 saved for your down payment. If you save $350 per pay, for the next 2 years, find the size of your available down payment. Assume you can earn 8% compounded monthly on all of your savings. Mc. Graw-Hill Ryerson© FV = 31430. 12 8 26 350 52 12 10000 Formula solution

Formula Solution 11 You already have $10000 saved for your down payment. If you save $350 per pay, for the next 2 years, find the size of your available down payment. Assume you can earn 8% compounded monthly on all of your savings. Mc. Graw-Hill Ryerson© 49 This is more complicated to solve when using algebraic equations! 3 Steps 1. Find the FV of the $10 000 in 2 years 2. Find the FV of the $350 per pay 3. Add totals together The $10 000 continues to earn interest during the new savings period!

50 Formula Solution 11 1. Formula FV = PV(1 + i)n = 10000(1 + 0. 08/12) 24 = $11, 728. 88 (1+ i) n - 1 FV = PMT 3. $ You already have 11, 728. 88 $10000 saved for your down 2. payment. If you i c-1 i 2 = (1+i) save $350 per pay, = (1+. 08/12). 4615 -1 for the next 2 years, find the size of your = 0. 0031 available down = 350 [(1+. 0031)52 – 1] payment. Assume you can earn 8%. 0031 = $19701. 24 19, 701. 24 compounded monthly Total 31, 430. 12 on all of your savings. [ Mc. Graw-Hill Ryerson© ]

11 Mc. Graw-Hill Ryerson© 51

11 52 A life insurance company advertises that $50, 000 will purchase a 20 -year annuity paying $341. 13 at the end of each month. What nominal rate of return does the annuity investment earn? C/Y = I/Y 12 240 1 50000 5. 54 1 341. 13 0 The annuity earns 5. 54% pa Mc. Graw-Hill Ryerson©

53 11 …to solve for i without a financial calculator Mc. Graw-Hill Ryerson©

54 11 This completes Chapter 11 Mc. Graw-Hill Ryerson©