11 -1 Статистические оценки и их свойства 11

11 -1 Статистические оценки и их свойства 11 -2 Интервальное оценивание параметров Доверительные интервалы для параметров нормального распределения 11 -4 Проверка статистических гипотез 11 -5 Критерий Пирсона

Определение статистической оценки •

Свойства статистических оценок (1) •

Свойства статистических оценок (2) •

Свойства статистических оценок (3) •

Точечные оценки •

Задача 1 • В школах города проведено тестирование школьников 11 класса по математике. Произвольно выбрано 7 тестов и записано количество баллов, набранных учениками: 28; 46; 12; 37; 53; 21; 48. Найти по полученной выборке… – несмещённую и состоятельную оценку математического ожидания М(Х) случайной величины Х – «количество баллов, полученных за тест» ; – несмещённую и состоятельную оценку дисперсии СВ Х; – несмещённую, состоятельную и эффективную оценку вероятности события А = «школьник наберёт большее чем 40 баллов» .

Решение задачи 1 • несмещённая и состоятельная оценка М(Х) есть среднее выборочное • несмещённая и состоятельная оценка D(X) есть исправленная выборочная дисперсия: • S = 15, 9 – несмещённая и состоятельная оценка σ(x).

Решение задачи 1 • несмещённой, состоятельной и эффективной оценкой вероятности события А = «школьник наберёт большее чем 40 баллов» является частота этого события Р(А) • После того, как точечная оценка параметра теоретического распределения получена, возникает задача определения надежности этой оценки.

Интервальное оценивание параметров •

Интервальное оценивание параметров • Часто доверительный интервал выбирается симметричным относительно несмещённой оценки параметра :

Доверительные интервалы для параметров нормального распределения (1) Доверительный интервал для неизвестного М(Х) = а при известной дисперсии D = σ2 и заданной доверительной вероятности задается следующим образом: t определяется из равенства 2 Ф(t) = , где Ф(t) функция Лапласа (табулирована). абсолютная (стандартная) ошибка среднего.

Доверительные интервалы для параметров нормального распределения (2) Доверительный интервал для неизвестного М(Х) = а при неизвестной дисперсии D = σ2 и заданной доверительной вероятности задается: где S исправленное среднее квадратическое отклонение; определяется по таблице квантилей распределения Стьюдента, α = 1 – – уровень значимости; k = n – 1 – число степеней свободы.

Доверительные интервалы для параметров нормального распределения (3) Доверительный интервал для неизвестной дисперсии D = σ2 при неизвестном М(Х) и заданной доверительной вероятности задается: где и находятся по таблице , k = n – 1 – число степеней свободы.

Доверительные интервалы для параметров нормального распределения (4) Доверительный интервал для оценки вероятности успеха при большом числе испытаний Бернулли: где

Задача 2 • Используя данные задачи 1, построить 95% доверительный интервал для математического ожидания а СВ Х – «количество баллов, полученных за тест» , если СВ Х распределена по нормальному закону.

Решение задачи 2 •

Решение задачи 2 • Вычислим стандартную ошибку среднего • Построим доверительный интервал: (35 -14, 7; 35+14, 7) • Ответ: Математическое ожидание а СВ Х попадёт в интервал (20, 3; 49, 7) с вероятностью 0, 95.

Число степеней свободы • Число степеней свободы определяется по количеству сведений, которое остаётся свободным после использования всей совокупности сведений для определения некоторой статистической характеристики. • Фиксирование объёма выборки и суммирование её значений накладывает на совокупность сведений одну линейную связь (всегда можно вычислить любое значение выборки, если другие значения известны и известно ). Значит число степеней свободы ν = n-1. • В биномиальном распределении и в распределении Пуассона учитываются 2 связи – одна связь, которая возникает при суммировании частот, вторая – связь, которая образуется при определении теоретических параметров распределения (р – при биномиальном и а для распределения Пуассона). Здесь число степеней свободы ν=n-2. При нормальном распределении ν=n-3, т. к. число параметров нормального распределения равно двум (a и ).

Статистические гипотезы • Статистическая гипотеза – всякое предположение о генеральной совокупности, проверяемое по выборке. Гипотезу нельзя доказать, её можно только принять или опровергнуть. • Проверкой статистических гипотез называется процедура сопоставления статистической гипотезы с выборочными данными. • Простая гипотеза – об одном значении параметра, в противном случае – сложная гипотеза.

Виды гипотез • основная или нулевая гипотеза и • H 1 - альтернативная гипотеза - логическое отрицание гипотезы H 0. • Например, H 0: различие средних значений двух совокупностей не значимо. Тогда H 1: различие средних статистически значимо. • Параметрические гипотезы - о параметрах распределения генеральной совокупности. • Непараметрические гипотезы - о неизвестном законе распределения генеральной совокупности.

Статистический критерий • Статистический критерий – правило, которое применяется для проверки гипотез. • Статистический критерий включает в себя: – формулу расчёта эмпирического критерия по выборочным данным; – формулу для определения числа степеней свободы; – теоретическое распределение для данного числа степеней свободы; – правило соотнесения эмпирического значения критерия с теоретическим распределением для определения вероятности того, что H 0 верна.

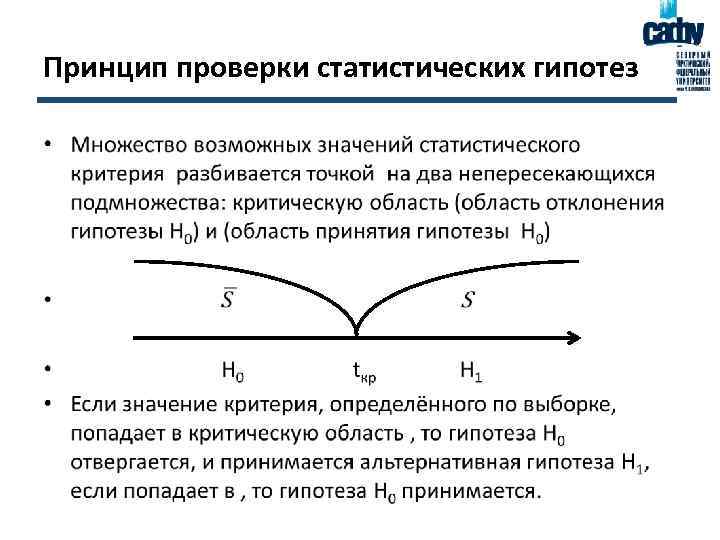Принцип проверки статистических гипотез •

Ошибки проверке гипотез • Гипотеза Отвергается Принимается верна неверна ошибка 1 -го рода ( α) правильное решение ошибка 2 -го рода (β)

Пример • Имеется программа машинного перевода текстов военнооперативной тематики с одного языка (язык противника или союзника) на другой. Качество программы проверяется экспериментально с помощью выборки. Можно сформулировать две гипотезы: первая - «программа пригодна и её можно принять на вооружение» и вторая – «программа непригодна для качественного перевода и её надо отвергнуть» • Если за H 0 принять первую гипотезу, то ошибка 1 -го рода будет заключаться в том, что программа пригодна, а её отправят на доработку, чем потеряют время и средства. • Если же за H 0 принять вторую гипотезу, то ошибка 1 -го рода будет заключаться в том, что программа непригодна, а её примут на вооружение, что может привести к срыву военной операции. Понятно, что за H 0 следует принять вторую гипотезу, т. к. ошибка 1 -го рода в случае её непринятия, более серьёзна.

Проверка гипотез с помощью непараметрических критериев • Для проверки непараметрических гипотез могут применяться различные критерии: – – – критерий Пирсона, критерий Колмогорова-Смирнова, критерий асимметрии и эксцесса, графический способ, упрощённые критерии (критерий Романовского, числа Вестергарда, вариационная сетка Турбина) и т п.

Критерий Пирсона • Для проверки нормальности распределения СВ Х (генеральной совокупности) по выборке необходимо выполнить следующее: • Сформировать нулевую H 0 (о том, что генеральная совокупность распределена по нормальному закону) и альтернативную H 1 гипотезы. • Выбрать уровень значимости ( чаще всего α=0, 05). • В полученном предварительно, интервальном статистическом ряде, объединить интервалы, количество наблюдений в которых меньше 5 (необходимым условием применения метода Пирсона является наличие в каждом интервале не менее 5 наблюдений , т. е. ni ≥ 5)

Критерий Пирсона •

Критерий Пирсона • Для каждого интервала найти произведение npi (теоретическая частота). Полученные результаты занести в таблицу : хi ni npi • Найти эмпирическое значение критерия Пирсона

Критерий Пирсона • Вычислить число степеней свободы по формуле k=m-r-1 , где m-число интервалов ряда, r- число параметров предполагаемого распределения (для нормального r=2). • По таблице 2 -распределения найти критическую точку . • Сделать вывод о принятии или опровержении нулевой гипотезы H 0 (если , то гипотеза H 0 принимается, если , то отвергается).

Пример • Используя результаты решения задачи 2 лекции 10, проверьте гипотезу о том, что рассматриваемая в задаче выборка произведена из нормально распределённой генеральной совокупности (т. е. СВ Х= «длина китайского слога» распределена по нормальному закону).

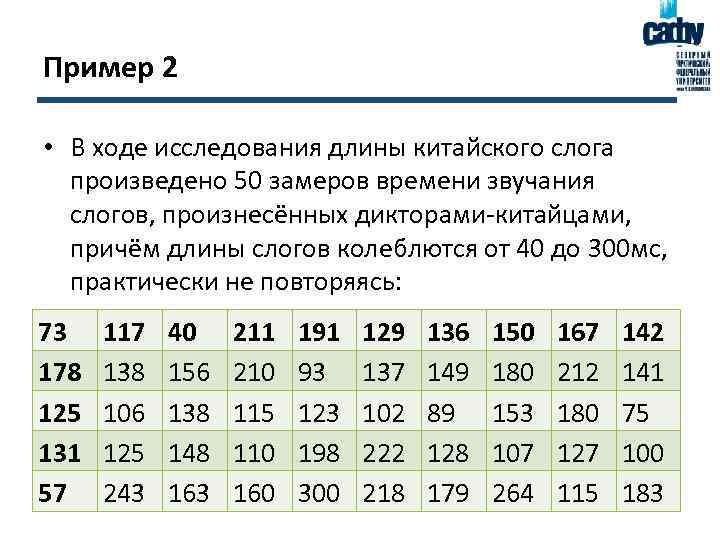Пример 2 • В ходе исследования длины китайского слога произведено 50 замеров времени звучания слогов, произнесённых дикторами-китайцами, причём длины слогов колеблются от 40 до 300 мс, практически не повторяясь: 73 178 125 131 57 117 138 106 125 243 40 156 138 148 163 211 210 115 110 160 191 93 123 198 300 129 137 102 222 218 136 149 89 128 179 150 180 153 107 264 167 212 180 127 115 142 141 75 100 183

Пример 2 • Построить интервальный статистический ряд по приведённым данным. Изобразить гистограмму относительных частот полученного распределения.

Решение • • Шаг 1 Проранжируем полученную выборку. Получим следующий вариационный ряд: 40; 57; 73; 75; 89; 93; 100; 102; 106; 107; 110; 115; 117; 123; 125; 127; 128; 129; 131; 136; 137; 138; 141; 142; 148; 149; 150; 153; 156; 160; 163; 167; 178; 179; 180; 183; 191; 198; 210; 211; 212; 218; 222; 243; 264; 300.

Пример 2 • Шаг 2 • Найдём оптимальную ширину интервалов

Пример 2 • Шаг 3 • Определим начало первого интервала

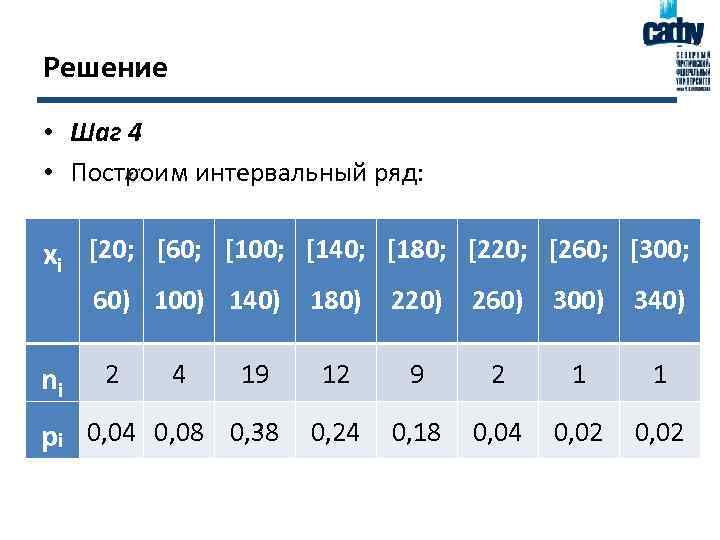Решение • Шаг 4 • Построим интервальный ряд: xi [20; [60; [100; [140; [180; [220; [260; [300; 60) 100) 140) ni 2 4 19 180) 220) 260) 300) 340) 12 9 2 1 1 pi 0, 04 0, 08 0, 38 0, 24 0, 18 0, 04 0, 02

Пример 2 • Шаг 5 • Найдём высоты прямоугольников, составляющих гистограмму относительных частот.

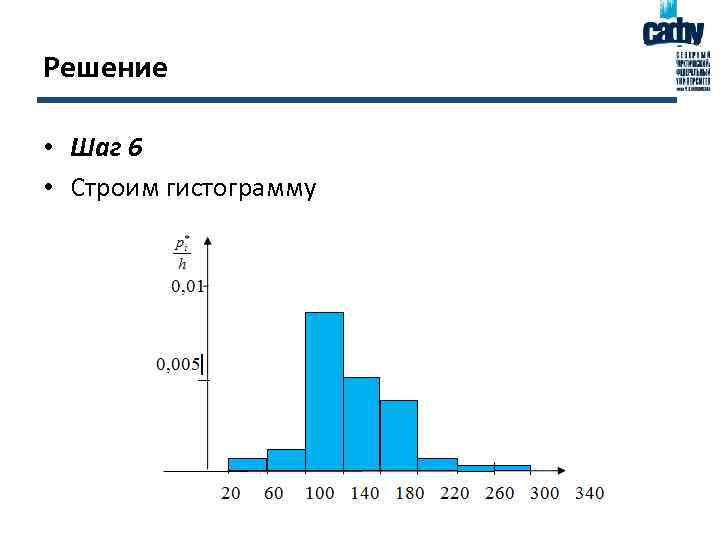Решение • Шаг 6 • Строим гистограмму