 1011011011101101111001101011001110101000111011011011011101101111001101011001110101000111011011011011101101111 0011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010 0011101101101101110110111100110101100111010100011101101101101110110111100110101100111010100011101101101101110 11011110011010110011101010001110110110110111011011110011010110011101010001110 110110110111100110101100111010100011101101110110111100110101100111010100011101101110110111 10011010110011101010001110110111011011110011010110011101010001110110110 Двоичное дерево Применение и классификация
1011011011101101111001101011001110101000111011011011011101101111001101011001110101000111011011011011101101111 0011010110011101010001110110110110111011011110011010110011101010001110110110110111011011110011010110011101010 0011101101101101110110111100110101100111010100011101101101101110110111100110101100111010100011101101101101110 11011110011010110011101010001110110110110111011011110011010110011101010001110 110110110111100110101100111010100011101101110110111100110101100111010100011101101110110111 10011010110011101010001110110111011011110011010110011101010001110110110 Двоичное дерево Применение и классификация
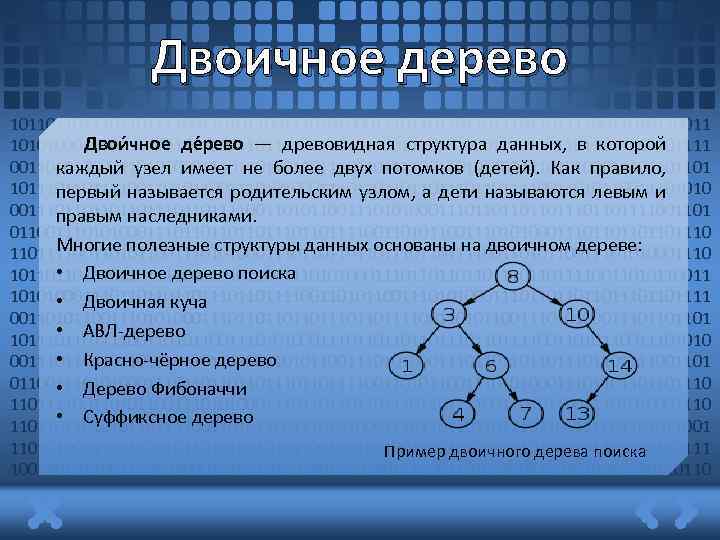 Двоичное дерево 1011011011110011010110011101010001110110111011011110011010110011 Двои чное де рево — древовидная структура данных, в которой 1010100011101101110110111100110101100111010100011101101110110111100110101100111010100011101101101 каждый узел имеет не более двух потомков (детей). Как правило, 1011011110011010110011101010001110110111011011110011010110011101010 первый называется родительским узлом, а дети называются левым и 00111011011101101111001101011001110101000111011011101101111001101 правым наследниками. 01100111010100011101101110110111100110101100111010100011101101110 Многие полезные структуры данных основаны на двоичном дереве: 11011110011010110011101010001110110111011011110011010110011101010001110 • Двоичное дерево поиска 101101101111001101011001110101000111011011101101111001101011001110101000111011011101101111 • Двоичная куча 00110101100111010100011101101110110111100110101100111010100011101101101 • АВЛ-дерево 1011011110011010110011101010001110110111011011110011010110011101010 • Красно-чёрное дерево 0011101101110110111100110101100111010100011101101110110111100110101100111010100011101101110 • Дерево Фибоначчи 11011110011010110011101010001110110111011011110011010110011101010001110 • Суффиксное дерево 110110110111100110101100111010100011101101110110111100110101100111010100011101101110110111 Пример двоичного дерева поиска 10011010110011101010001110110111011011110011010110011101010001110110110
Двоичное дерево 1011011011110011010110011101010001110110111011011110011010110011 Двои чное де рево — древовидная структура данных, в которой 1010100011101101110110111100110101100111010100011101101110110111100110101100111010100011101101101 каждый узел имеет не более двух потомков (детей). Как правило, 1011011110011010110011101010001110110111011011110011010110011101010 первый называется родительским узлом, а дети называются левым и 00111011011101101111001101011001110101000111011011101101111001101 правым наследниками. 01100111010100011101101110110111100110101100111010100011101101110 Многие полезные структуры данных основаны на двоичном дереве: 11011110011010110011101010001110110111011011110011010110011101010001110 • Двоичное дерево поиска 101101101111001101011001110101000111011011101101111001101011001110101000111011011101101111 • Двоичная куча 00110101100111010100011101101110110111100110101100111010100011101101101 • АВЛ-дерево 1011011110011010110011101010001110110111011011110011010110011101010 • Красно-чёрное дерево 0011101101110110111100110101100111010100011101101110110111100110101100111010100011101101110 • Дерево Фибоначчи 11011110011010110011101010001110110111011011110011010110011101010001110 • Суффиксное дерево 110110110111100110101100111010100011101101110110111100110101100111010100011101101110110111 Пример двоичного дерева поиска 10011010110011101010001110110111011011110011010110011101010001110110110
 Двоичное дерево поиска 1011011011110011010110011101010001110110111011011110011010110011 Двоичное дерево поиска (англ. binary search tree, BST) — это двоичное 10101000111011011101101111001101011001110101000111011011101101111 дерево, для которого выполняются следующие дополнительные 00110101100111010100011101101110110111100110101100111010100011101101101 условия (свойства дерева поиска): 101101111001101011001110101000111011011101101111001101011001110101000111011011101101111001101 • Оба поддерева — левое и правое, являются двоичными деревьями 01100111010100011101101110110111100110101100111010100011101101110 поиска. 11011110011010110011101010001110110111011011110011010110011101010001110 • У всех узлов левого поддерева произвольного узла X значения 1011011011110011010110011101010001110110111011011110011010110011 ключей данных меньше, нежели значение ключа данных узла X. 10101000111011011101101111001101011001110101000111011011101101111 • У всех узлов правого поддерева произвольного узла X значения 00110101100111010100011101101110110111100110101100111010100011101101101 ключей данных больше, нежели значение ключа данных узла X. 1011011110011010110011101010001110110111011011110011010110011101010 (Данные обладают ключом, на котором определена операция 00111011011101101111001101011001110101000111011011101101111001101 сравнения "меньше". ) 01100111010100011101101110110111100110101100111010100011101101110 Двоичное дерево поиска применяется для построения более 11011110011010110011101010001110110111011011110011010110011101010001110 абстрактных структур, таких как множества, мультимножества, 1101101101111001101011001110101000111011011101101111001101011001 ассоциативные массивы. 1101010001110110111011011110011010110011101010001110110111011011110011010110011101010001110110110
Двоичное дерево поиска 1011011011110011010110011101010001110110111011011110011010110011 Двоичное дерево поиска (англ. binary search tree, BST) — это двоичное 10101000111011011101101111001101011001110101000111011011101101111 дерево, для которого выполняются следующие дополнительные 00110101100111010100011101101110110111100110101100111010100011101101101 условия (свойства дерева поиска): 101101111001101011001110101000111011011101101111001101011001110101000111011011101101111001101 • Оба поддерева — левое и правое, являются двоичными деревьями 01100111010100011101101110110111100110101100111010100011101101110 поиска. 11011110011010110011101010001110110111011011110011010110011101010001110 • У всех узлов левого поддерева произвольного узла X значения 1011011011110011010110011101010001110110111011011110011010110011 ключей данных меньше, нежели значение ключа данных узла X. 10101000111011011101101111001101011001110101000111011011101101111 • У всех узлов правого поддерева произвольного узла X значения 00110101100111010100011101101110110111100110101100111010100011101101101 ключей данных больше, нежели значение ключа данных узла X. 1011011110011010110011101010001110110111011011110011010110011101010 (Данные обладают ключом, на котором определена операция 00111011011101101111001101011001110101000111011011101101111001101 сравнения "меньше". ) 01100111010100011101101110110111100110101100111010100011101101110 Двоичное дерево поиска применяется для построения более 11011110011010110011101010001110110111011011110011010110011101010001110 абстрактных структур, таких как множества, мультимножества, 1101101101111001101011001110101000111011011101101111001101011001 ассоциативные массивы. 1101010001110110111011011110011010110011101010001110110111011011110011010110011101010001110110110
 Двоичная куча 1011011011110011010110011101010001110110111011011110011010110011 • Двои чная ку ча, пирами да, или сортиру ющее де рево — такое 10101000111011011101101111001101011001110101000111011011101101111 двоичное дерево, для которого выполнены три условия: 001101011001110101000111011011101101111001101011001110101000111011011011110011010110011101010001110110111011011110011010110011101010 • Значение в любой вершине не меньше, чем значения её потомков. 00111011011101101111001101011001110101000111011011101101111001101 • Каждый лист имеет глубину (расстояние до корня) либо d-1. 01100111010100011101101110110111100110101100111010100011101101110 Иными словами, если назвать слоем совокупность вершин, 11011110011010110011101010001110110111011011110011010110011101010001110 находящихся на определённой глубине, то все слои, кроме, быть 1011011011110011010110011101010001110110111011011110011010110011 может, последнего, заполнены полностью. 1010100011101101110110111100110101100111010100011101101110110111100110101100111010100011101101101 • Последний слой заполняется слева направо. 101101111001101011001110101000111011011101101111001101011001110101000111011011101101111001101 Применяется в алгоритмах где необходимо 0110011101010001110110111011011110011010110011101010001110110111011011110011010110011101010001110 быстро извлекать макс. /мин. элемент 1101101101111001101011001110101000111011011101101111001101011001 (например, в пирамидальной сортировке, 11010100011101101110110111100110101100111010100011101101110110111 алгоритме Дейкстры). 10011010110011101010001110110111011011110011010110011101010001110110110
Двоичная куча 1011011011110011010110011101010001110110111011011110011010110011 • Двои чная ку ча, пирами да, или сортиру ющее де рево — такое 10101000111011011101101111001101011001110101000111011011101101111 двоичное дерево, для которого выполнены три условия: 001101011001110101000111011011101101111001101011001110101000111011011011110011010110011101010001110110111011011110011010110011101010 • Значение в любой вершине не меньше, чем значения её потомков. 00111011011101101111001101011001110101000111011011101101111001101 • Каждый лист имеет глубину (расстояние до корня) либо d-1. 01100111010100011101101110110111100110101100111010100011101101110 Иными словами, если назвать слоем совокупность вершин, 11011110011010110011101010001110110111011011110011010110011101010001110 находящихся на определённой глубине, то все слои, кроме, быть 1011011011110011010110011101010001110110111011011110011010110011 может, последнего, заполнены полностью. 1010100011101101110110111100110101100111010100011101101110110111100110101100111010100011101101101 • Последний слой заполняется слева направо. 101101111001101011001110101000111011011101101111001101011001110101000111011011101101111001101 Применяется в алгоритмах где необходимо 0110011101010001110110111011011110011010110011101010001110110111011011110011010110011101010001110 быстро извлекать макс. /мин. элемент 1101101101111001101011001110101000111011011101101111001101011001 (например, в пирамидальной сортировке, 11010100011101101110110111100110101100111010100011101101110110111 алгоритме Дейкстры). 10011010110011101010001110110111011011110011010110011101010001110110110
 АВЛ-дерево 1011011011110011010110011101010001110110111011011110011010110011 АВЛ-дерево — сбалансированное по высоте двоичное дерево поиска: 1010100011101101110110111100110101100111010100011101101110110111100110101100111010100011101101101 для каждой его вершины высота её двух поддеревьев различается не 1011011110011010110011101010001110110111011011110011010110011101010 более чем на 1. 00111011011101101111001101011001110101000111011011101101111001101 АВЛ — аббревиатура, образованная первыми буквами создателей 01100111010100011101101110110111100110101100111010100011101101110 (советских учёных) Адельсон-Вельского, Георгия Максимовича и Е. М. 11011110011010110011101010001110110111011011110011010110011101010001110 Ландиса. 101101101111001101011001110101000111011011101101111001101011001110101000111011011101101111 Применяется в основном в поисковых машинах. 00110101100111010100011101101110110111100110101100111010100011101101101111001101011001110101000111011011101101111001101011001110101000111011011101101111001101 0110011101010001110110111011011110011010110011101010001110110111011011110011010110011101010001110 110110110111100110101100111010100011101101110110111100110101100111010100011101101110110111 10011010110011101010001110110111011011110011010110011101010001110110110
АВЛ-дерево 1011011011110011010110011101010001110110111011011110011010110011 АВЛ-дерево — сбалансированное по высоте двоичное дерево поиска: 1010100011101101110110111100110101100111010100011101101110110111100110101100111010100011101101101 для каждой его вершины высота её двух поддеревьев различается не 1011011110011010110011101010001110110111011011110011010110011101010 более чем на 1. 00111011011101101111001101011001110101000111011011101101111001101 АВЛ — аббревиатура, образованная первыми буквами создателей 01100111010100011101101110110111100110101100111010100011101101110 (советских учёных) Адельсон-Вельского, Георгия Максимовича и Е. М. 11011110011010110011101010001110110111011011110011010110011101010001110 Ландиса. 101101101111001101011001110101000111011011101101111001101011001110101000111011011101101111 Применяется в основном в поисковых машинах. 00110101100111010100011101101110110111100110101100111010100011101101101111001101011001110101000111011011101101111001101011001110101000111011011101101111001101 0110011101010001110110111011011110011010110011101010001110110111011011110011010110011101010001110 110110110111100110101100111010100011101101110110111100110101100111010100011101101110110111 10011010110011101010001110110111011011110011010110011101010001110110110
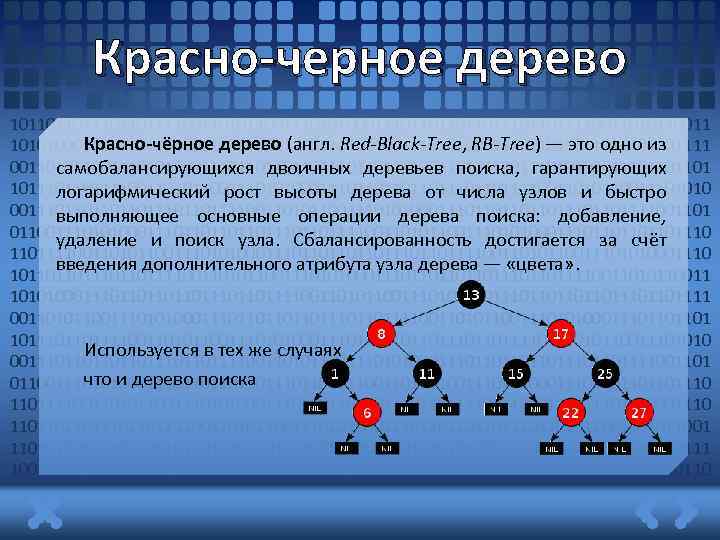 Красно-черное дерево 1011011011110011010110011101010001110110111011011110011010110011 Красно-чёрное дерево (англ. Red-Black-Tree, RB-Tree) — это одно из 1010100011101101110110111100110101100111010100011101101110110111100110101100111010100011101101101 самобалансирующихся двоичных деревьев поиска, гарантирующих 1011011110011010110011101010001110110111011011110011010110011101010 логарифмический рост высоты дерева от числа узлов и быстро 00111011011101101111001101011001110101000111011011101101111001101 выполняющее основные операции дерева поиска: добавление, 01100111010100011101101110110111100110101100111010100011101101110 удаление и поиск узла. Сбалансированность достигается за счёт 11011110011010110011101010001110110111011011110011010110011101010001110 введения дополнительного атрибута узла дерева — «цвета» . 101101101111001101011001110101000111011011101101111001101011001110101000111011011101101111 001101011001110101000111011011101101111001101011001110101000111011011011110011010110011101010001110110111011011110011010110011101010 Используется в тех же случаях 00111011011101101111001101011001110101000111011011101101111001101 что и дерево поиска 0110011101010001110110111011011110011010110011101010001110110111011011110011010110011101010001110 110110110111100110101100111010100011101101110110111100110101100111010100011101101110110111 10011010110011101010001110110111011011110011010110011101010001110110110
Красно-черное дерево 1011011011110011010110011101010001110110111011011110011010110011 Красно-чёрное дерево (англ. Red-Black-Tree, RB-Tree) — это одно из 1010100011101101110110111100110101100111010100011101101110110111100110101100111010100011101101101 самобалансирующихся двоичных деревьев поиска, гарантирующих 1011011110011010110011101010001110110111011011110011010110011101010 логарифмический рост высоты дерева от числа узлов и быстро 00111011011101101111001101011001110101000111011011101101111001101 выполняющее основные операции дерева поиска: добавление, 01100111010100011101101110110111100110101100111010100011101101110 удаление и поиск узла. Сбалансированность достигается за счёт 11011110011010110011101010001110110111011011110011010110011101010001110 введения дополнительного атрибута узла дерева — «цвета» . 101101101111001101011001110101000111011011101101111001101011001110101000111011011101101111 001101011001110101000111011011101101111001101011001110101000111011011011110011010110011101010001110110111011011110011010110011101010 Используется в тех же случаях 00111011011101101111001101011001110101000111011011101101111001101 что и дерево поиска 0110011101010001110110111011011110011010110011101010001110110111011011110011010110011101010001110 110110110111100110101100111010100011101101110110111100110101100111010100011101101110110111 10011010110011101010001110110111011011110011010110011101010001110110110
 Дерево фибоначчи 1011011011110011010110011101010001110110111011011110011010110011 Дерево Фибоначчи — АВЛ-дерево с наименьшим числом вершин при 1010100011101101110110111100110101100111010100011101101110110111100110101100111010100011101101101 заданной высоте (глубине). 1011011110011010110011101010001110110111011011110011010110011101010 • Если для какой-либо из вершин высота поддерева, для которого эта 00111011011101101111001101011001110101000111011011101101111001101 вершина является корнем, равна h, то правое и левое поддерево 01100111010100011101101110110111100110101100111010100011101101110 этой вершины имеют высоты равные соответственно h − 1 и h − 2, 11011110011010110011101010001110110111011011110011010110011101010001110 или h − 2 и h − 1. Каждое поддерево дерева Фибоначчи также 1011011011110011010110011101010001110110111011011110011010110011 является деревом Фибоначчи. 1010100011101101110110111100110101100111010100011101101110110111100110101100111010100011101101101 • Пустое дерево — дерево Фибоначчи высоты 0. 1011011110011010110011101010001110110111011011110011010110011101010 • Дерево с одной вершиной — дерево Фибоначчи высоты 1. 00111011011101101111001101011001110101000111011011101101111001101 Используется в тех же случаях что и АВЛ-дерево. 0110011101010001110110111011011110011010110011101010001110110111011011110011010110011101010001110 110110110111100110101100111010100011101101110110111100110101100111010100011101101110110111 10011010110011101010001110110111011011110011010110011101010001110110110
Дерево фибоначчи 1011011011110011010110011101010001110110111011011110011010110011 Дерево Фибоначчи — АВЛ-дерево с наименьшим числом вершин при 1010100011101101110110111100110101100111010100011101101110110111100110101100111010100011101101101 заданной высоте (глубине). 1011011110011010110011101010001110110111011011110011010110011101010 • Если для какой-либо из вершин высота поддерева, для которого эта 00111011011101101111001101011001110101000111011011101101111001101 вершина является корнем, равна h, то правое и левое поддерево 01100111010100011101101110110111100110101100111010100011101101110 этой вершины имеют высоты равные соответственно h − 1 и h − 2, 11011110011010110011101010001110110111011011110011010110011101010001110 или h − 2 и h − 1. Каждое поддерево дерева Фибоначчи также 1011011011110011010110011101010001110110111011011110011010110011 является деревом Фибоначчи. 1010100011101101110110111100110101100111010100011101101110110111100110101100111010100011101101101 • Пустое дерево — дерево Фибоначчи высоты 0. 1011011110011010110011101010001110110111011011110011010110011101010 • Дерево с одной вершиной — дерево Фибоначчи высоты 1. 00111011011101101111001101011001110101000111011011101101111001101 Используется в тех же случаях что и АВЛ-дерево. 0110011101010001110110111011011110011010110011101010001110110111011011110011010110011101010001110 110110110111100110101100111010100011101101110110111100110101100111010100011101101110110111 10011010110011101010001110110111011011110011010110011101010001110110110
 Суффиксное дерево 1011011011110011010110011101010001110110111011011110011010110011 Суффиксное дерево — бор, содержащий все суффиксы некоторой 1010100011101101110110111100110101100111010100011101101110110111100110101100111010100011101101101 строки (и только их). Позволяет выяснять, входит ли строка w в 1011011110011010110011101010001110110111011011110011010110011101010 исходную строку t, за время O(|w|), где |w| — длина строки w. 00111011011101101111001101011001110101000111011011101101111001101 (Префиксное дерево (бор) — абстрактный тип данных, структура 01100111010100011101101110110111100110101100111010100011101101110 данных, позволяющая хранить ассоциативный массив, ключами 11011110011010110011101010001110110111011011110011010110011101010001110 которого являются строки. ) 101101101111001101011001110101000111011011101101111001101011001110101000111011011101101111 00110101100111010100011101101110110111100110101100111010100011101101101 Используется для обработки 1011011110011010110011101010001110110111011011110011010110011101010 строк 0011101101110110111100110101100111010100011101101110110111100110101100111010100011101101110 11011110011010110011101010001110110111011011110011010110011101010001110 1101101101111001101011001110101000111011011101101111001101011001 Суффиксное дерево для строки xabxa$ 1101010001110110111011011110011010110011101010001110110111011011110011010110011101010001110110110
Суффиксное дерево 1011011011110011010110011101010001110110111011011110011010110011 Суффиксное дерево — бор, содержащий все суффиксы некоторой 1010100011101101110110111100110101100111010100011101101110110111100110101100111010100011101101101 строки (и только их). Позволяет выяснять, входит ли строка w в 1011011110011010110011101010001110110111011011110011010110011101010 исходную строку t, за время O(|w|), где |w| — длина строки w. 00111011011101101111001101011001110101000111011011101101111001101 (Префиксное дерево (бор) — абстрактный тип данных, структура 01100111010100011101101110110111100110101100111010100011101101110 данных, позволяющая хранить ассоциативный массив, ключами 11011110011010110011101010001110110111011011110011010110011101010001110 которого являются строки. ) 101101101111001101011001110101000111011011101101111001101011001110101000111011011101101111 00110101100111010100011101101110110111100110101100111010100011101101101 Используется для обработки 1011011110011010110011101010001110110111011011110011010110011101010 строк 0011101101110110111100110101100111010100011101101110110111100110101100111010100011101101110 11011110011010110011101010001110110111011011110011010110011101010001110 1101101101111001101011001110101000111011011101101111001101011001 Суффиксное дерево для строки xabxa$ 1101010001110110111011011110011010110011101010001110110111011011110011010110011101010001110110110


