c22641d9ebb7c17620d34539555e88ca.ppt
- Количество слайдов: 52

10 TH EDITION COLLEGE ALGEBRA LIAL HORNSBY SCHNEIDER 5. 7 - 1

5. 7 Properties of Matrices Basic Definitions Adding Matrices Special Matrices Subtracting Matrices Multiplying Matrices Applying Matrix Algebra 5. 7 - 2

Basic Definitions It is customary to use capital letters to name matrices. Also, subscript notation is often used to name elements of a matrix, as in the following matrix A. 5. 7 - 3

Basic Definitions Certain matrices have special names: an n x n matrix is a square matrix because the number of rows is equal to the number of columns. A matrix with just one row is a row matrix, and a matrix with just one column is a column matrix. 5. 7 - 4

Basic Definitions Two matrices are equal if they are the same size and if corresponding elements, position by position, are equal. Using this definition, the matrices and are not equal (even though they contain the same elements and are the same size), since the corresponding elements differ. 5. 7 - 5

Example 1 FINDING VALUES TO MAKE TWO MATRICES EQUAL Find the values of the variables for which each statement is true, if possible. a. Solution From the definition of equality, the only way that the statement can be true is if 2 = x, 1 = y, p = – 1 and q = 0. 5. 7 - 6

Example 1 FINDING VALUES TO MAKE TWO MATRICES EQUAL Find the values of the variables for which each statement is true, if possible. b. Solution This statement can never be true since the two matrices are different sizes. (One is 2 1 and the other is 3 1. ) 5. 7 - 7

Addition of Matrices To add two matrices of the same size, add corresponding elements. Only matrices of the same size can be added. 5. 7 - 8

Example 2 ADDING MATRICES Find each sum, if possible. a. Solution 5. 7 - 9
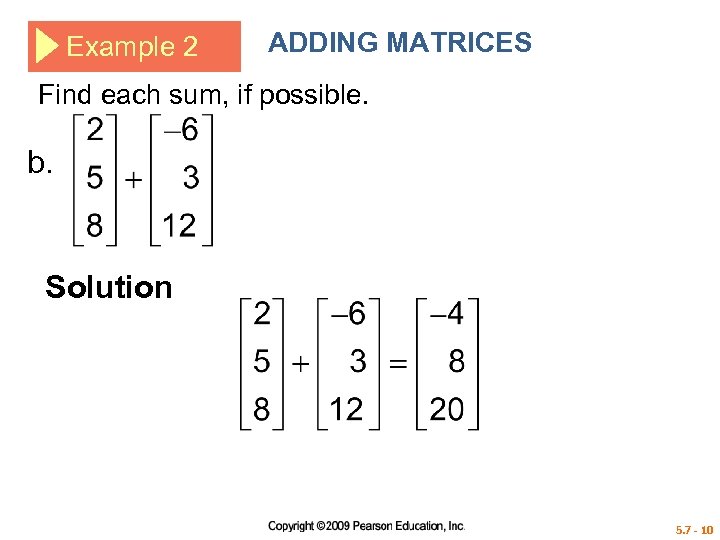
Example 2 ADDING MATRICES Find each sum, if possible. b. Solution 5. 7 - 10

Example 2 ADDING MATRICES Find each sum, if possible. c. A + B, if A = and B = Solution The matrices and have different sizes so A and B cannot be added; the sum does not exist. 5. 7 - 11

Special Matrices A matrix containing only zero elements is called a zero matrix. A zero matrix can be written with any size. 1 3 zero matrix 2 3 zero matrix 5. 7 - 12

Special Matrices By the additive inverse property, each real number has an additive inverse: if a is a real number, then there is a real number such that 5. 7 - 13

Special Matrices Given matrix A, there is a matrix – A such that A + (– A) = . The matrix – A has as elements the additive inverses of the elements of A. (Remember, each element of A is a real number and therefore has an additive inverse. ) For example, if 5. 7 - 14

Special Matrices To check, test that A + (– A) equals the zero matrix, O Matrix – A is called the additive inverse, or negative, of matrix A. Every matrix has an additive inverse. 5. 7 - 15

Subtraction of Matrices If A and B are two matrices of the same size, then A – B = A + (– B). 5. 7 - 16

Example 3 SUBTRACTING MATRICES Find each difference, if possible. a. Solution 5. 7 - 17

Example 3 SUBTRACTING MATRICES Find each difference, if possible. b. Solution 5. 7 - 18

Example 3 SUBTRACTING MATRICES Find each difference, if possible. c. A – B, if A = and B = Solution The matrices and have different sizes and cannot be subtracted, so the difference does not exist. 5. 7 - 19
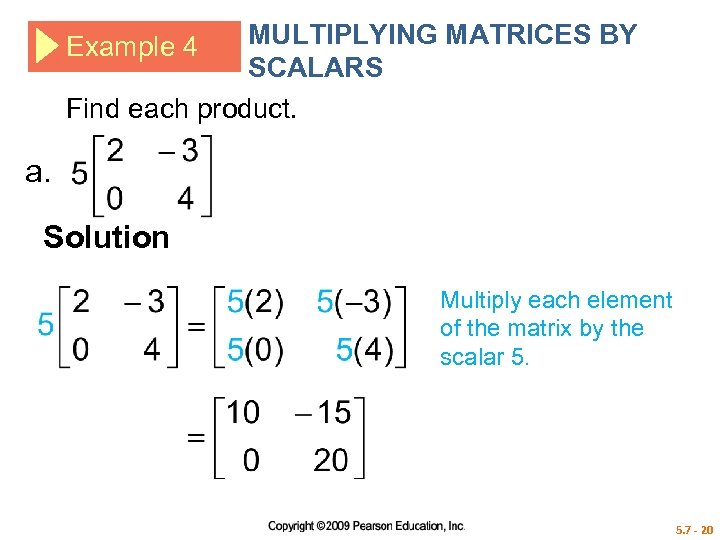
MULTIPLYING MATRICES BY SCALARS Find each product. Example 4 a. Solution Multiply each element of the matrix by the scalar 5. 7 - 20
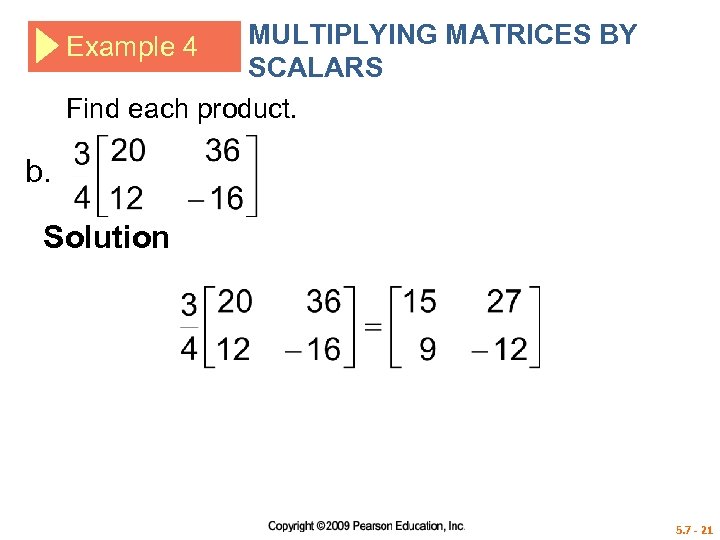
MULTIPLYING MATRICES BY SCALARS Find each product. Example 4 b. Solution 5. 7 - 21

Properties of Scalar Multiplication If A and B are matrices of the same size and c and d are scalars, then 5. 7 - 22

Matrix Multiplication We have seen how to multiply a real number (scalar) and a matrix. To find the product of two matrices, such as 5. 7 - 23

Matrix Multiplication first locate row 1 of A and column 1 of B, shown shaded below. 5. 7 - 24

Matrix Multiplication Multiply corresponding elements, and find the sum of the products. This result is the element for row 1, column 1 of the product matrix. Now use row 1 of A and column 2 of B to determine the element in row 1, column 2 of the product matrix. 5. 7 - 25

Matrix Multiplication Next, use row 2 of A and column 1 of B; this will give the row 2, column 1 entry of the product matrix. Finally, use row 2 of A and column 2 of B to find the entry for row 2, column 2 of the product matrix. 5. 7 - 26

Matrix Multiplication The product matrix can now be written. 5. 7 - 27

Matrix Multiplication To find the ith row, jth column element of AB, multiply each element in the ith row of A by the corresponding element in the jth column of B. (Note the shaded areas in the matrices below. ) The sum of these products will give the row i, column j element of AB. 5. 7 - 28

Matrix Multiplication 5. 7 - 29

Matrix Multiplication 5. 7 - 30

Matrix Multiplication The number of columns of an m n matrix A is the same as the number of rows of an n p matrix B (i. e. , both n). The element cij of the product matrix C = AB is found as follows: Matrix AB will be an m p matrix. 5. 7 - 31

DECIDING WHETHER TWO MATRICES CAN BE MULTIPLIED Suppose A is a 3 2 matrix, while B is a 2 4 matrix. Example 5 a. Can the product AB be calculated? Solution The following diagram shows that AB can be calculated, because the number of columns of A is equal to the number of rows of B. (Both are 2. ) Matrix A Matrix B 3 2 2 4 must match size of AB 3 4 5. 7 - 32
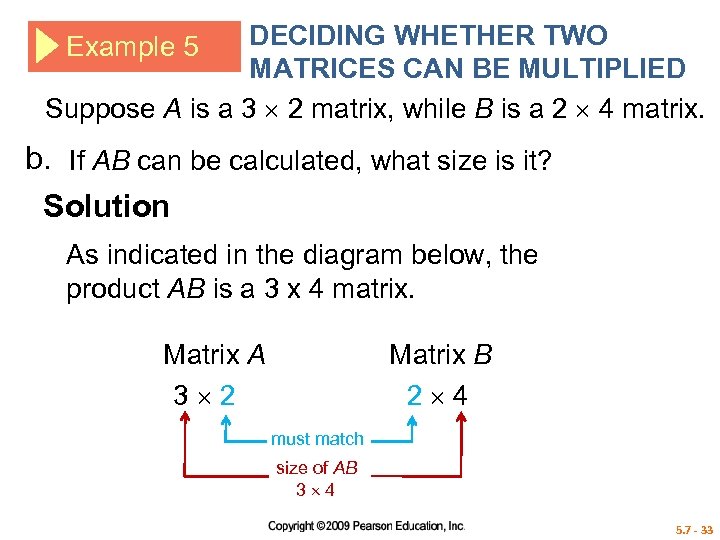
DECIDING WHETHER TWO MATRICES CAN BE MULTIPLIED Suppose A is a 3 2 matrix, while B is a 2 4 matrix. Example 5 b. If AB can be calculated, what size is it? Solution As indicated in the diagram below, the product AB is a 3 x 4 matrix. Matrix A 3 2 Matrix B 2 4 must match size of AB 3 4 5. 7 - 33

DECIDING WHETHER TWO MATRICES CAN BE MULTIPLIED Suppose A is a 3 2 matrix, while B is a 2 4 matrix. Example 5 c. Can BA be calculated? Solution The diagram below shows that BA cannot be calculated. Matrix B 3 4 Matrix A 3 4 different 5. 7 - 34

DECIDING WHETHER TWO MATRICES CAN BE MULTIPLIED Suppose A is a 3 2 matrix, while B is a 2 4 matrix. Example 5 d. If BA can be calculated, what size is it? Solution The product BA cannot be calculated, because B has 4 columns and A has only 3 rows. 5. 7 - 35

Example 6 MULTIPLYING MATRICES Let Find each product, if possible. a. AB Solution First decide whether AB can be found. Since A is 2 2 and B is 2 4, the product can be found and will be a 2 4 matrix. 5. 7 - 36

Example 6 MULTIPLYING MATRICES Use the definition of matrix multiplication Perform the operations. 5. 7 - 37

Example 6 MULTIPLYING MATRICES Let Find each product, if possible. b. BA Solution Since B is a 2 4 matrix, and A is a 2 2 matrix, the number of columns of B (4) does not equal the number of rows of A (2). Therefore, the product BA cannot be found. 5. 7 - 38

Example 7 SQUARE Let Find each product. a. AB Solution 5. 7 - 39

Example 7 SQUARE Let Find each product. b. BA Solution Note that AB ≠ BA. 5. 7 - 40

In general, if A and B are matrices, then AB ≠ BA. Matrix multiplication is not commutative. 5. 7 - 41

Properties of Matrix Multiplication If A, B, and C are matrices such that all the following products and sums exist, then 5. 7 - 42

Example 8 USING MATRIX MULTIPLICATION TO MODEL PLANS FOR A SUBDIVISION A contractor builds three kinds of houses, models A, B, and C, with a choice of two styles, colonial or ranch. Matrix P shows the number of each kind of house the contractor is planning to build for a new 100 -home subdivision. The amounts for each of the main materials used depend on the style of the house. These amounts are shown in matrix Q, while matrix R gives the cost in dollars for each kind of material. Concrete is measured here in cubic yards, lumber in 1000 board feet, brick in 1000 s, and shingles in 100 square feet. 5. 7 - 43

Example 8 USING MATRIX MULTIPLICATION TO MODEL PLANS FOR A SUBDIVISION Colonial Ranch Model A Model B Model C 5. 7 - 44

Example 8 USING MATRIX MULTIPLICATION TO MODEL PLANS FOR A SUBDIVISION Concrete Lumber Brick Shingles Colonial Ranch 5. 7 - 45

Example 8 USING MATRIX MULTIPLICATION TO MODEL PLANS FOR A SUBDIVISION Cost per Unit Concrete Lumber Brick Shingles 5. 7 - 46

Example 8 USING MATRIX MULTIPLICATION TO MODEL PLANS FOR A SUBDIVISION a. What is the total cost of materials for all houses of each model? Solution To find the materials cost for each model, first find matrix PQ, which will show the total amount of each material needed for all houses of each model. 5. 7 - 47

Example 8 Concrete USING MATRIX MULTIPLICATION TO MODEL PLANS FOR A SUBDIVISION Lumber Brick Shingles Model A Model B Model C 5. 7 - 48

Example 8 USING MATRIX MULTIPLICATION TO MODEL PLANS FOR A SUBDIVISION Multiplying PQ and the cost matrix R gives the total cost of materials for each model. Cost Model A Model B Model C 5. 7 - 49

Example 8 USING MATRIX MULTIPLICATION TO MODEL PLANS FOR A SUBDIVISION b. How much of each of the four kinds of material must be ordered? Solution To find how much of each kind of material to order, refer to the columns of matrix PQ. The sums of the elements of the columns will give a matrix whose elements represent the total amounts of each material needed for the subdivision. Call this matrix T, and write it as a row matrix. 5. 7 - 50

Example 8 USING MATRIX MULTIPLICATION TO MODEL PLANS FOR A SUBDIVISION c. What is the total cost of the materials? Solution The total cost of all the materials is given by the product of matrix T, the total amounts matrix, and matrix R, the cost matrix. To multiply these and get a 1 1 matrix, representing the total cost, requires multiplying a 1 4 matrix and a 4 1 matrix. This is why in part (b) a row matrix was written rather than a column matrix. The total materials cost is given by TR, so 5. 7 - 51

Example 8 USING MATRIX MULTIPLICATION TO MODEL PLANS FOR A SUBDIVISION The total cost of materials is $188, 400. 5. 7 - 52
c22641d9ebb7c17620d34539555e88ca.ppt