10 AM Harshada Gandhi will present SENTIMENT ANALYSIS

10 AM Harshada Gandhi will present: SENTIMENT ANALYSIS – CHALLENGES AND ALTERNATIVES TO IMPROVE ACCURACY: 11 AM Rajesh Subramaniam semantic analysis, in particular developing a contextual relevance to words depending on frequency of appearance of pairs in text corpus. Note that there will no meeting on May 16 due to NDSU Commencement on that day. FEEDBACK TO ALL STUDENTS REGARDING THE WRITING OF PAPERS (and proposals and theses): The main criticism (constructive!) of most papers )including student papers) is inadequate background research (inaccurate and/or incomplete). E. g. , A paper on “community mining” (AKA clique_mining/Cohesive_Subgraph_Mining/clustering/Near_Neighbor_Mining…) one needs to carefully / completely summarize (in enough detail so the entire audience you are trying to reach can understand it) WHAT HAS BEEN DONE ALREADY BY OTHERS right up until the current moment! E. g. , below I found a “communities” paper by a known author dated last month. In it Yancey points to the Fortunato survey to describe the area and the frontier (nearly up-to-the-present). Next you should point out even more clearly, what your paper is going to do to ADVANCE that body of work (and where it will fit (and be reported in the next paper in this genre). All papers are refereed (even proposals)! As soon as a referee decides you don’t know the area and its frontiers, they reject the paper (and should). On the other hand, if you are meticulous on this, you can impress the #@$!% out of a referee by demonstrating an up-to-the-minute understanding of the topic (and impress even more if you correctly summarize (i. e. , praise) his/her own previous work). So a paper must do 3 things: 1. accurately describe the topic frontier up-to-the-moment (make use of the Saturday Notes Online Repository (SNOR)); 2. clearly describe your addition (how are you nudging that frontier outward); 3. prove that it is an addition (it is a nudge worth reading about). And your paper must do these 3 things 3 times (in the Abstract/Intro “tell um what you are going to do (the 3 things)”; in the body “do the 3 things” and in the conclusion “tell um what you told um (the 3 things)”. So “tell um what you’re going to tell um; tell um what you told um” Bipartite Communities Matthew P. Yancey April 15, 2015 A recent trend in data-mining is finding communities in a graph. A community is a vertex set s. t. # edges inside it is > expected. Many ways to assess this (cliques in social networks, families of proteins in protein-protein interaction networks, constructing groups of similar products in recommendation systems… ) An up-to-the moment survey on community detection: S. Fortunato, “Community Detection in Graphs. “ ar. Xiv 0906. 0612 v 2. 3. 2. Communities 3. 2. 1. Basics In graph clustering, we look for a quantitative definition of community. No definition is universally accepted. As a matter of fact, the definition often depends on the specific system at hand and/or application one has in mind. Intuitively, a community has more edges “inside” the community than edges linking vertices of the community to the outside. Communities can be algorithmically defined i. e. they are just the final product of an algorithm, without a precise a priori def. Let us start with a subgraph C of a graph G, with C having nc and G having n vertices, respectively. The internal and external degree of vertex v∈C, kvint, kvext, are the number of edges connecting v to other vertices of C, to the rest of graph. If kvext=0, the vertex has neighbors only within C, which is likely to be a good cluster for v; if kvint=0, instead, the vertex is disjoint from C and it should be better assigned to a different cluster. The internal degree kint. C of C is the sum of the internal degrees of its vertices. The external degree kext. C of C is the sum of the external degrees of its vertices. The total degree k. C is the sum of the degrees of the vertices of C. By definition, k. C=kint. C+kext. C. intra-cluster density δint(C) = # of internal edges of C over # of all possible internal edges, i. e. δint(C) = # internal edges of C / (nc(nc− 1)/2) inter-cluster density δext(C) = # of edges from vertices of C over # of inter-cluster edges possible, δext(C)=# inter-cluster edges of C / (nc(n−nc). For C to be a community we expect δint(C) to be appreciably larger than the average link density δ(G) of G (ratio between the number of edges of G and the maximum number of possible edges n(n− 1)/2. δext(C) has to be much smaller than δ(G)δ. Finding the best tradeoff between large δint(C) and small δext(C) is implicitly or explicitly the goal of most clustering algs. A simple way to do that is, e. g. , maximizing the sum of the differences δint(C)−δext(C) over all clusters of the partition. connectedness : If C is a community there must be a path between each pair of its vertices, running only thru vertices of C. We give 3 classes of definitions: local, global and based on vertex similarity. Others are defined by algs introducing them.

3. 2. 2. Local definitions: Local definitions focus on subgraph, incl. possibly its immediate neighborhood but neglecting the rest of the graph. Communities are mostly maximal subgraphs (addition of new vertices and edges destroys the property which defines them). Social communities can be defined in a very strict sense as subgroups whose members are all “friends” (complete mutuality). In graph terms, this corresponds to a clique, i. e. a subset whose vertices are all adjacent to each other. In social network analysis, a clique is a maximal subgraph. Graph theory also calls non-maximal subgraphs cliques. Triangles are the simplest cliques, and are frequent in real networks. But larger cliques are less frequent (condition is too strict: a subgraph with all possible internal edges except one would be an extremely cohesive subgroup, but it would not be considered a community under this recipe). Another problem is that all vertices of a clique are absolutely symmetric. Vertices may belong to more cliques simultaneously, a property at the basis of the Clique Percolation Method of Palla et al. From a practical point of view, finding cliques in a graph is an NP-complete problem. It is however possible to relax the notion of clique, defining subgroups which are still clique-like objects. A possibility is to use properties related to reachability, i. e. to the existence (and length) of paths between vertices. An n-clique is a maximal subgraph s. t. the distance of each pair of its vertices is not larger than n (n=1 is a clique. This definition still has some limitations: paths may run on vertices outside the subgraph. This has several problems. The diameter of the subgraph may exceed n. The subgraph may be disconnected, which is not cohesion. Mokken [72] suggests n-clan and n-club. n-clan is an n-clique whose diameter n. n-club, instead, is a maximal subgraph of diameter n. Difference? n-clan is maximal under the constraint of being an n-clique. An n-club is maximal under the constraint imposed by diameter length. Another criterion relies on vertex adjacency. A vertex must be adjacent to a minimum number of other vertices in subgraph. In social network lit, a k-plex is a maximal subgraph s. t. each vertex is adjacent to all other vertices of subgraph except at most k of them [73]. Similarly, a k-core is a maximal subgraph in which each vertex is adjacent to at least k other vertices of the subgraph [74]. Both impose conditions on min # of absent or present edges. Clusters are more cohesive than n-cliques, due to existence of many internal edges. In any graph there is a whole hierarchy of cores of different order, which can be identified with a recent efficient algorithm. A k-core is the same as a p-quasi complete subgraph (degree of each vertex > p(k− 1), p is a real number in [0, 1] and k the order of the subgraph. As cohesive as a subgraph can be, it would hardly be a community if there is also strong cohesion with the rest of the graph. Compare the internal and external cohesion of a subgraph is what is usually done in the recent definitions of community. An LS-set, or strong community, is a subgraph s. t. internal degree of each vertex > its external degree. Relaxed into weak community (the internal degree > its external degree). LS-set is also a weak community, while converse is not generally true. alt defs: strong if internal vertex degree > # edges vertex shares with any other community; weak if total internal degree > #edges shared w others These definitions are in the same spirit of the planted partition model. An LS-set is also a strong community. edge connectivity of pair of vertices = min # edges to be removed to disconnect the two vertices, i. e. such that there is no path between them. lambda set is subgraph s. t. any vertex pair has larger edge connectivity than any pair with 1 vertex inside and 1 outside. Vertices may be distant. A fitness measure is the extent a subgraph satisfies a given property related to its cohesion (Simplest: δint(C). One could assume that a subgraph C with k vertices is a cluster if δint(C) > ξ. NP-complete problem, as it coincides with the NP-complete Clique Problem when the threshold ξ=1. Need to six subgraph size, else any clique would be one of the best possible communities, including trivial two-cliques (simple edges). Variants of this problem focus on the number of internal edges of the subgraph [81], [82] and [83]. relative density, ρ(C) = ratio between internal and total degree of C. Finding subgraphs of a given size with ρ(C) >Thresh NP-complete [84]. Fitness measures can also be associated to the connectivity of the subgraph at study to the other vertices of the graph. A good community is expected to have small cut size (see Appendix A. 1) (small # of edges joining it to the rest of the graph). This sets a bridge between community detection and graph partitioning, which we shall discuss in Section 4. 1.

3. 2. 4. Definitions based on vertex similarity: It is natural to assume that communities are groups of similar vertices. One can compute the similarity between each pair of vertices with respect to some reference property, local or global, no matter whether they are connected by an edge or not. Each vertex ends up in the cluster whose vertices are most similar to it. Adjacency Matrix Distance [39] [3] dij=∑k≠i, j(Aik−Ajk)2 (A=adjacency matrix). Shared nbr based, even if not adjacent. Measure the overlap between the nbhds Γ(i), Γ(j) of vertices i, j given by ωij=|Γ(i)∩Γ(j)||Γ(i)∪Γ(j)|. Pearson correlation between adjacency matrix rows/cols, Cij=∑k(Aik−μi)(Ajk−μj)/nσiσj, μi=(∑j. Aij)/n, σi=∑j(Aij−μi)2/n. Use number of edge- (or vertex-) independent paths between two vertices. Independent paths do not share any edge (vertex). Commute-time (avg # of steps for a random walker to reach the other vertex and come back. [91], [92], [93] [94] [97] [98] used avg first passage time, i. e. avg # of steps needed to reach for the first time the target vertex from the source. escape probability (prob walker reaches target vertex before returning to source [102] [103]. Related to conductance. Properties of modified random walks. [104] [103]. Similarity measures derived from Google’s Page. Rank process [56]. Embedding vertices in n-space (assign a position), distance between a pair of vertices is a measure of dissimilarity. cosine similarity, ρab = arccos( a⋅b / |a||b| ) where a⋅b is the dot product of the vectors a and b. ρAB is in range [0, π). 3. 3. Partitions is a division into clusters with each vertex in 1 (not unquely). Division into overlapping (or fuzzy) communities is called cover. The number of possible partitions into k clusters of a graph with n vertices is the Stirling number of second kind S(n, k) [105]. n-th Bell # Bn=∑k=0 n. S(n, k) total # partitions. Asymptotic form Bn∼ 1 n[λ(n)]n+1/2 eλ(n)−n− 1 (λ(n)=e. W(n)=n/W(n), W(n) Lambert Wfunction Partitions can be hierarchically ordered, when the graph has different levels of organization/structure at different scales. Clusters display in turn community structure with smaller communities inside which may again contain smaller communities. As an example, in a social network of children living in the same town, one could group the children according to the schools they attend, but within each school one can make a subdivision into classes. Hierarchical organization is a common feature of many real networks (use a dendrogram? ) Cutting the diagram horizontally at some height, as shown in the figure (dashed line), displays one partition of the graph. The diagram is hierarchical: each community belonging to a level is fully included in a community at a higher level. Dendrograms are regularly used in sociology and biology. Reliable algorithms are supposed to identify good partitions. But what is a good clustering? For “good” and “bad” clusterings, we might require partitions satisfy a set of basic properties, intuitive and easy to agree. Given a set S of pts, a distance function d is defined, which is positive definite and symmetric (no triangular inequality req). One wishes to find a clustering f based on the distances between the points. Kleinberg showed that no clustering satisfies at the same time three following properties: 1. Scale-invariance : given a constant αα, multiplying any distance function dd by αα yields the same clustering. 2. Richness : any possible partition of the given point set can be recovered if one chooses a suitable distance function dd. 3. Consistency: given a partition, any modification of the distance function that does not decrease the distance between points of different clusters and that does not increase the distance between points of the same cluster, yields the same clustering. The theorem cannot be extended to graph clustering. Distance cannot be in general defined for a graph that’s not complete. For weighted complete graphs, like correlation matrices [112], it is often possible to define a distance function. On a generic graph, except for property 1, which does not make sense without a distance, the other two are quite well defined. Richness implies that, given a partition, one can set edges between the vertices in such a way that the partition is a natural outcome of the resulting graph (e. g. , it could be achieved by setting edges only between vertices of the same cluster). Consistency here implies that deleting inter-cluster edges and adding intra-cluster edges yields the same partition.

A C, is confident if a high fraction of the f F which are related to every a A, are also related to every c C F is the Focus Entity and the high fraction is the Minimum. Confidence ratio. A hop is a relationship, R, hopping from entity, E, to entity, F. Supp. Set. A (set of F’s related to every element of A) = {2, 3, 5} F Supp. Set. C = {2, 4, 5} Strong Rule Mining finds all frequent, confident rules 2/3 = Conf. A C = |Supp. Set. A C|/|Supp. Set. A| SRMs are categorized by the number of hops, k, 4 = ct(&e A CPe) / ct(&e APe) A whether transitive or non-transitive and by the focus entity. 3 2 ARM is 1 -hop, non-transitive (A, C E), F-focused SRM (1 n. F) 1 0 0 1 1 1 0 1 C 2 1 -hop, transitive (A E, C F), F-focused SRM (1 t. F) ct(&e ARe &PC) / ct(&e ARe) mncf antecedent downward closure: If A is frequent, all subsets are frequent (A is infrequent, supersets infreq) Since frequency involves only A, we can mine for all qualifying antecedents using downward closure. E 1 1 0 0 F 5 1 1 1 ct(&e ARe) mnsp 3 4 1 1 1 0 1 1 R(E, F) Question: Why isn’t Conf. A C = Supp. C / Supp. A? consequent upward closure: If A C is non-confident, then so is A D for all subsets, D, of C. So frequent antecedent, A, use upward closure to mine for all of its' confident consequents. Transitive (a+c)-hop Apriori strong rule mining with a focus entity which is a hops from the antecedent and c hops from the consequent, if a/c is odd/even then one can use downward/upward closure on that step in the mining of strong (frequent and confident) rules. C G S(F, G) In this case A is 1 -hop from F (odd, use downward closure). C is 0 -hops from F (even, use upward closure). 1 1 0 0 4 1 0 0 0 3 0 1 1 1 2 1 0 0 1 1 2 3 4 5 4 0 1 3 0 0 0 1 2 0 0 1 0 0 0 1 We will be checking more examples to see if the Odd downward Even upward theorem seems to hold. |A|=ct(PA) mnsp 1 -hop, transitive, E-focused rule, A C SRM (1 t. E) ct(PA&f CRf) / ct(PA) mncf antecedent upward closure: If A is infrequent, then so are all of its subsets. consequent downward closure) If A C is non-confident, then so is A D for all supersets, D, of C. In this case A is 0 -hops from E (even, use upward closure). 2 -hop transitive F-focused C is 1 -hop from E (odd, use downward closure). A C strong if: ct(&e ARe) mnsp and A E ct(&e ARe &g CSg) / ct(&e ARe) mncf F R(E, F) 1, 1 odd so down, down correct. Apriori for 2 -hops: Find all freq antecedents, A, using downward closure. 2, 0 even so up, up is correct. find C 1 G, the set of g's s. t. A {g} is confident. 0, 2 even so up, up is correct. Find C 2 G, set of C 1 G pairs that are confident consequents for antecedent, A. Find C 3 G, set of triples (from C 2 G) s. t. all subpairs are in C 2 G (ala Apriori), etc. ct(&f list& Re. Sf & PC) / &f list& Re. Sf mncf 2 -hop trans G-foc ct(&f list&e ARe. Sf) mnsp e A ct(&f l& Re. Sf) mnsp ct(&f & R Sf & PC) / &f & R Sf mncf 2 -hop trans E-foc ct(PA) mnsp ct(PA&f & Sg. Rf ) / ct(PA) mncf e A g C e e e A antecedent upward closure: If A is infrequent, so are all subsets. 1. (antecedent upward closure) If A is infrequent, then so for are all subsets. 2. (consequent upward closure) If A C non-conf, so is A D for all subsets, D. consequent upward closuree: If A C non-conf so is A D for all subsets, D.

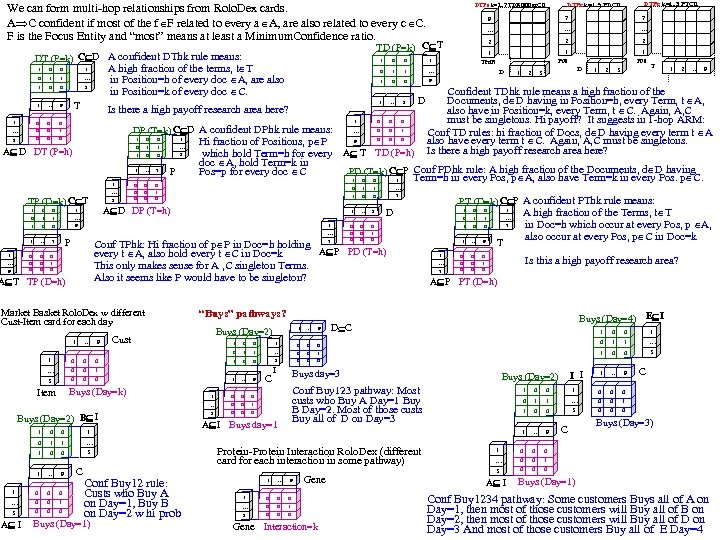We can form multi-hop relationships from Rolo. Dex cards. A C confident if most of the f F related to every a A, are also related to every c C. F is the Focus Entity and “most” means at least a Minimum. Confidence ratio. 1 0 0 1 1 … 1 0 0 3 1 … 9 1 0 0 0 … 0 0 1 3 0 0 0 T 0 1 1 1 A D DT (P=h) 0 0 0 … 3 1 1 … 3 TP (D=k) C T 1 0 0 1 1 1 0 0 … 9 1 … 7 0 0 0 0 1 0 7 0 0 0 P 0 1 0 … 9 1 0 0 D 0 … 1 0 1 1 1 0 0 1 … 1 3 Market Basket Rolo. Dex w different Cust-Item card for each day 1 Pos Term D Pos T 1 2 D 3 1 2 3 … 9 0 0 0 1 … 7 1 1 0 0 … 7 1 1 0 1 0 0 0 1 Buys (Day=2) … 9 0 0 0 0 1 0 T Is this a high payoff research area? A P PT (D=h) … 9 Buys (Day=4) E I D C 1 0 0 1 1 Cust 0 0 1 1 … 0 0 1 1 0 0 3 3 0 0 0 1 … 9 0 0 0 0 1 0 0 … 0 0 1 0 1 … 9 1 0 0 0 … 0 0 1 3 0 0 0 Buys (Day=k) Item Buys (Day=2) B I 1 0 0 1 1 … 1 0 0 3 1 … 9 1 0 0 0 … 0 0 1 0 3 A I C C I Buys day=3 Buys (Day=2) I I Conf Buy 123 pathway: Most custs who Buy A Day=1 Buy B Day=2. Most of those custs Buy all of D on Day=3 Protein-Protein Interaction Rolo. Dex (different card for each interaction in some pathway) … Buys (Day=1) 1 … 9 1 0 0 0 … 0 0 1 3 0 0 Gene Interaction=k A I 0 1 1 1 … 1 1 0 0 3 1 A I Buys day=1 1 3 Conf Buy 12 rule: Custs who Buy A on Day=1, Buy B on Day=2 w hi prob … 9 A high fraction of the Terms, t T in Doc=h which occur at every Pos, p A, also occur at every Pos, p C in Doc=k “Buys” pathways? 1 3 2 PT (D=k) C P A confident PThk rule means: D 0 1 1 Confident TDhk rule means a high fraction of the Documents, d D having in Position=h, every Term, t A, also have in Position=k, every Term, t C. Again, A, C must be singletons. Hi payoff? It suggests in 1 -hop ARM: Conf TD rules: hi fraction of Docs, d D having every term t A also have every term t C. Again, A, C must be singletons. Is there a high payoff research area here? … 7 Conf TPhk: Hi fraction of p P in Doc=h holding 7 A P PD (T=h) every t A, also hold every t C in Doc=k This only makes sense for A , C singleton Terms. Also it seems like P would have to be singleton? A T TP (D=h) 1 9 … 2 1 … 0 … 2 0 0 0 9 Hi fraction of Positions, p P TD (P=h) which hold Term=h for every A T doc A, hold Term=k in PD (T=k) C P Conf PDhk rule: A high fraction of the Documents, d D having Pos=p for every doc C Term=h in every Pos, p A, also have Term=k in every Pos. p C. 1 0 0 1 1 P 1 0 1 A D DP (T=h) 1 0 … 0 0 0 1 7 … 2 1 1 DP (T=k) C D A confident DPhk rule means: 1 0 0 Is there a high payoff research area here? 0 7 … 1 A high fraction of the terms, t T in Position=h of every doc A, are also in Position=k of every doc C. 1 0 9 TD (P=k) C T DT (P=k) C D A confident DThk rule means: DTPe k=1. . 3 PTCd DTPe k=1. . 9 PDCd DTPe k=1. . 7 TDRolodex. Cd … 9 0 0 0 C 0 1 0 C Buys (Day=3) Buys (Day=1) Conf Buy 1234 pathway: Some customers Buys all of A on Day=1, then most of those customers will Buy all of B on Day=2, then most of those customers will Buy all of D on Day=3 And most of those customers Buy all of E Day=4

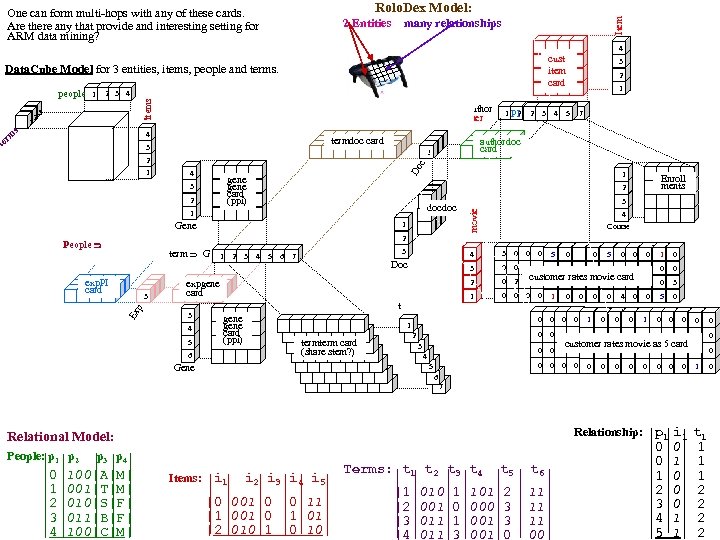2 Entities Item Rolo. Dex Model: One can form multi-hops with any of these cards. Are there any that provide and interesting setting for ARM data mining? many relationships 4 cust item card Data. Cube Model for 3 entities, items, people and terms. 3 2 1 People Author Customer te rm s 4 termdoc card 3 1 1 4 gene card (ppi) 3 2 1 1 1 PI 3 4 4 5 2 2 3 5 6 7 1 authordoc 1 1 card 1 1 1 Do c 2 1 1 1 docdoc 1 1 Gene 1 Enroll ments 2 1 3 movie 2 3 4 5 1 items people 3 4 Course 2 People term G exp. PI card 1 1 3 4 5 6 3 7 Ex 4 3 0 0 Doc 3 0 0 2 2 0 2 1 0 0 0 expgene card 3 4 5 gene card (ppi) 6 4 5 0 1 0 0 3 0 0 5 0 0 0 0 0 1 0 0 4 0 0 0 1 0 customer rates movie card 0 2 Gene 5 0 1 term card (share stem? ) 0 0 t p 3 1 3 5 0 0 0 customer rates movie as 5 card 0 0 0 1 6 7 Relationship: p 1 i 1 t 1 Relational Model: People: p 1 p 2 |0 |1 |2 |3 |4 p 3 p 4 100|A|M| 001|T|M| 010|S|F| 011|B|F| 100|C|M| Items: i 1 i 2 i 3 i 4 i 5 |0 001|0 |0 11| |1 001|0 |1 01| |2 010|1 |0 10| Terms: t 1 t 2 t 3 t 4 |1 |2 |3 |4 010|1 001|0 011|1 011|3 t 5 101|2 000|3 001|0 t 6 11| 11| 00| |0 |0 |1 |2 |3 |4 |5 0 0| 1 1| 1 0| 2 1|_2 0

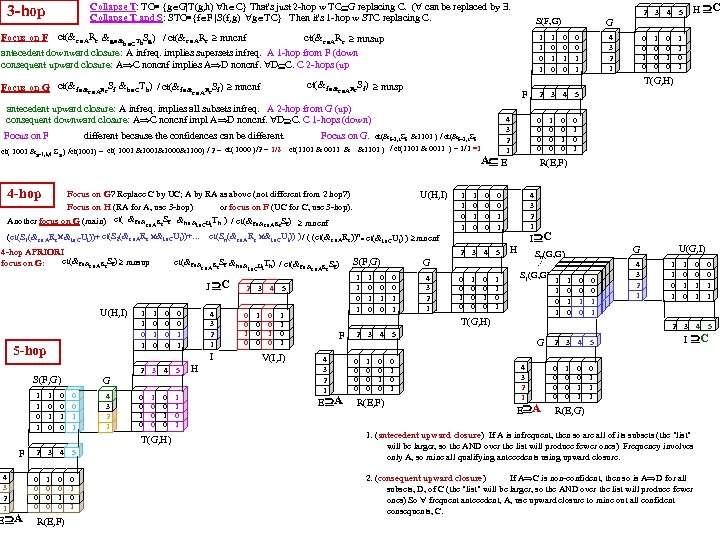Collapse T: TC≡ {g G|T(g, h) h C} That's just 2 -hop w TC G replacing C. ( can be replaced by . Collapse T and S: STC≡{f F |S(f, g) g TC} Then it's 1 -hop w STC replacing C. 3 -hop Re Focus on F ct(&e A &g & Th. Sg) / ct(&e ARe mncnf ct(&e ARe mnsup h C antecedent downward closure: A infreq. implies supersets infreq. A 1 -hop from F (down consequent upward closure: A C noncnf implies A D noncnf. D C. C 2 -hops (up A E U(H, I) Focus on G? Replace C by UC; A by RA as above (not different from 2 hop? ) Focus on H (RA for A, use 3 -hop) or focus on F (UC for C, use 3 -hop). Another focus on G (main) ct( &f &e ARe. Sf &h &i CUi. Th ) / ct(&f &e ARe. Sf) mncnf J C U(H, I) 0 0 0 1 1 3 4 5 0 0 1 0 0 0 1 1 0 1 0 0 0 1 0 G 0 0 1 1 4 3 2 1 T(G, H) F 4 3 2 1 E A 4 3 2 1 I S(F, G) 1 1 0 1 0 2 5 -hop 1 1 0 1 2 3 4 5 0 0 0 0 1 0 1 0 R(E, F) H 2 3 4 1 0 0 0 1 1 0 1 V(I, J) 1 0 0 0 1 0 0 0 1 1 2 3 4 1 0 0 1 0 1 4 4 3 2 1 E A 0 0 1 0 R(E, F) 1 0 0 0 1 1 0 1 5 1 0 0 0 1 0 1 4 3 2 1 3 4 5 4 3 2 1 I C H 4 3 2 1 0 0 0 1 1 0 1 U(G, I) G Sn(G, G) 1 0 0 0 1 1 1 0 11 00 00 11 1 1 0 0 1 G 4 3 2 1 E A 2 3 4 5 0 0 1 0 0 0 4 3 2 1 1 1 0 1 0 2 1 S 1(G, G) 1111 110 000 11 00 00 0 1 00 11 11 11 0 0 0 5 0 0 3 T(G, H) F 0 0 1 0 H C 5 R(E, F) 0 0 1 1 G 1 1 0 1 5 0 0 1 0 S(F, G) 0 0 1 1 . . . ct(&f &e ARe. Sf &h & Ui. Th) / ct(&f & R Sf) e A e i C 1 1 0 1 2 ct(S 2(&e ARe &i CUi))+. . . ct(Sn(&e ARe &i CUi)) ) / ( (ct(&e ARe))n * ct(&i CUi) ) mncnf (ct(S 1(&e ARe &i CUi))+ 4 -hop APRIORI ct(&f &e ARe. Sf) mnsup focus on G: 0 0 1 0 0 0 4 3 2 1 ct(&f=2, 5 Sf &1101 ) / ct(1101 & 0011 ) = 1/1 =1 4 -hop 4 T(G, H) Focus on F different because the confidences can be different. Focus on G. ct(1101 & 0011 & 1 0 2 F antecedent upward closure: A infreq. implies all subsets infreq. A 2 -hop from G (up) consequent downward closure: A C noncnf impl A D noncnf. D C. C 1 -hops (down) ct( 1001 &g=1, 3, 4 Sg ) /ct(1001) = ct( 1001 &1001&1000&1100) / 2 = ct( 1000 )/2 = 1/2 3 G 1 1 0 1 ct(&f &e ARe. Sf) mnsp ct(&f &e ARe. Sf &h CTh) / ct(&f & Re. Sf) mncnf Focus on G e A 2 S(F, G) 3 I 0 0 1 1 4 5 C 0 1 1 1 0 0 1 1 R(E, G) 1. (antecedent upward closure) If A is infrequent, then so are all of its subsets (the "list" will be larger, so the AND over the list will produce fewer ones) Frequency involves only A, so mine all qualifying antecedents using upward closure. 2. (consequent upward closure) If A C is non-confident, then so is A D for all subsets, D, of C (the "list" will be larger, so the AND over the list will produce fewer ones) So frequent antecedent, A, use upward closure to mine out all confident consequents, C.

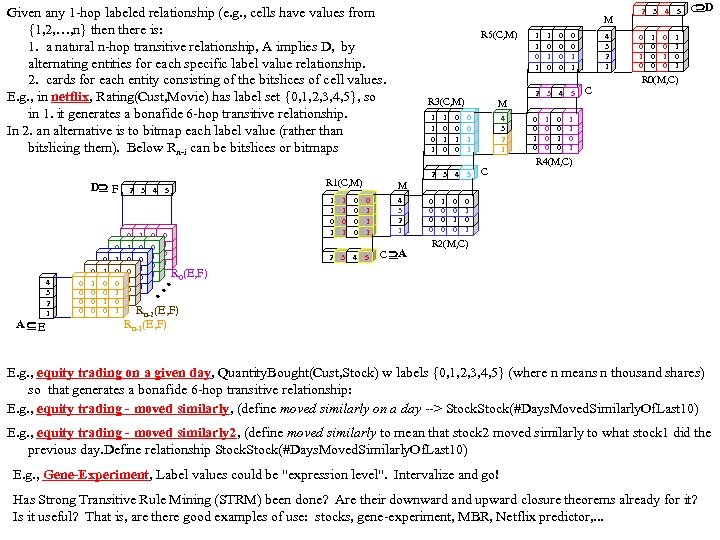Given any 1 -hop labeled relationship (e. g. , cells have values from {1, 2, …, n} then there is: 1. a natural n-hop transitive relationship, A implies D, by alternating entities for each specific label value relationship. 2. cards for each entity consisting of the bitslices of cell values. E. g. , in netflix, Rating(Cust, Movie) has label set {0, 1, 2, 3, 4, 5}, so in 1. it generates a bonafide 6 -hop transitive relationship. In 2. an alternative is to bitmap each label value (rather than bitslicing them). Below Rn-i can be bitslices or bitmaps A E 4 3 2 1 0 0 0 0 1 0 0 0 0 0 1 1 0 0 1 2 0 0 1 0 0 0 0 1 1 0 0 1 3 4 1 0 0 0 1 1 0 0 1 0 1 1 1 0 1 2 1 1 0 0 0 0 3 4 R 3(C, M) 1 1 0 1 0 0 0 0 1 1 2 3 4 5 0 0 1 0 1 0 0 0 0 0 1 0 C D 1 1 0 1 4 3 2 1 C R 0(M, C) M 1 1 0 1 0 0 0 1 1 2 R 1(C, M) 5 R 5(C, M) 2 3 4 5 0 0 0 0 1 0 1 4 3 2 1 C R 4(M, C) M 0 1 1 1 5 4 3 2 1 C A 0 0 1 0 R 2(M, C) R 0(E, F) . . . D F M Rn-2(E, F) Rn-1(E, F) E. g. , equity trading on a given day, Quantity. Bought(Cust, Stock) w labels {0, 1, 2, 3, 4, 5} (where n means n thousand shares) so that generates a bonafide 6 -hop transitive relationship: E. g. , equity trading - moved similarly, (define moved similarly on a day --> Stock(#Days. Moved. Similarly. Of. Last 10) E. g. , equity trading - moved similarly 2, (define moved similarly to mean that stock 2 moved similarly to what stock 1 did the previous day. Define relationship Stock(#Days. Moved. Similarly. Of. Last 10) E. g. , Gene-Experiment, Label values could be "expression level". Intervalize and go! Has Strong Transitive Rule Mining (STRM) been done? Are their downward and upward closure theorems already for it? Is it useful? That is, are there good examples of use: stocks, gene-experiment, MBR, Netflix predictor, . . .

Let Types be an entity which clusters Items (moves Items up the semantic hierarchy), Buys(C, T) 1 1 0 1 0 0 0 1 1 4 3 2 1 2 3 4 5 Customers 20 19 18 17 16 15 0 0 0 1 0 0 0 0 1 1 1 14 13 0 0 0 1 1 E. g. , in a store, Types might include; dairy, hardware, household, canned, snacks, baking, meats, produce, bakery, automotive, electronics, toddler, boys, girls, women, pharmacy, garden, toys, farm). Let A be an Item. Set wholly of one Type, TA, and l et D by a Types. Set which does not include TA. Then: A D might mean If i A s. t. BB(i, c) then t T, B(c, t) A D confident might mean ct(&i ABBi &t DBt) / ct(&i ABBi) mncf ct(&i ABBi | t DBt) / ct(&i ABBi) mncf ct( | i ABBi | t DBt) / ct( | i ABBi) mncf ct( | i ABBi &t DBt) / ct( | i ABBi) mncf D Types (of Items) A Items 12 11 8 7 0 0 0 1 6 5 0 0 0 1 1 4 3 0 0 0 1 1 2 1 0 0 0 1 1 10 9 Bought. By(I, C, ) A D frequent might mean ct(&i ABBi) mnsp ct( | i ABBi) mnsp ct(&t DBt) mnsp ct( | t DBt) mnsp ct(&i ABBi &t DBt) mnsp, etc.

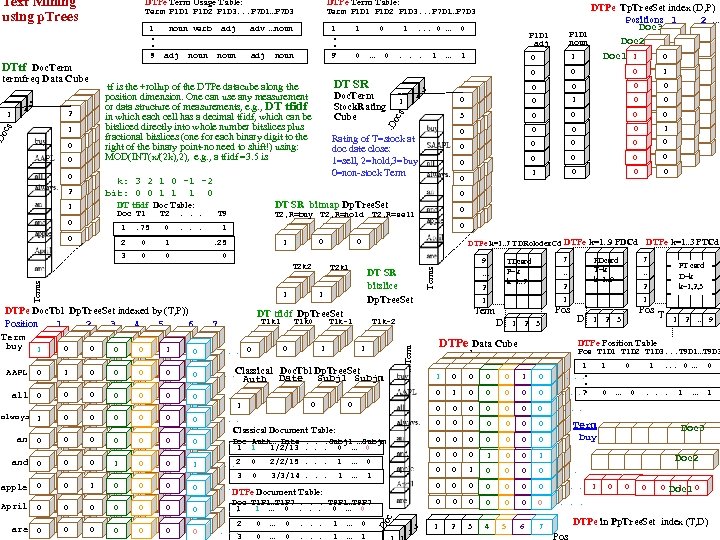Text Mining using p. Trees DTPe Term Usage Table: noun 0 0 0 DT tfidf Doc Table: 1 Doc T 1 0 T 2 . . . Doc. Term Stock. Rating Cube . . . 0 2 0 1 0 0 Terms T 1 k 1 0 . 0 0 1 0 0 Classical 0 . all 0 0 0 always 1 0 an 0 1 0 3 0 0 0 0 1 0 0 0 10 0 00 0 10 0 0 0 0 0 0 DTPe k=1. . 7 TDRolodex. Cd DTPe k=1. . 9 PDCd T 2 k 1 T 1 k 0 0 . 1 0 0 DT SR bitslice Dp. Tree. Set 1 0 0 0 3 2 T 2, R=sell DT tfidf Dp. Tree. Set 7 0 0 0 1 0 0 … P 1 D 1 adj 0 . 25 DTPe Doc. Tbl Dp. Tree. Set indexed by (T, P)) Position 1 2 3 4 5 6 Term AAPL 1 1 1 . 75 T 2, R=buy T 2, R=hold 1 0 . . . Rating of T=stock at doc date close: 1=sell, 2=hold, 3=buy 0=non-stock Term T 2 k 2 1 0 0 DT SR bitmap Dp. Tree. Set T 9 3 buy … . . . 0 … 0 1 0 0 1 DT SR k: 3 2 1 0 -1 -2 bit: 0 0 1 1 1 0 2 0 T 1 k-1 1 9 Terms oc adj 1 . . . 9 . D 1 . D noun 1 tf is the +rollup of the DTPe datacube along the position dimension. One can use any measurement or data structure of measurements, e. g. , DT tfidf in which each cell has a decimal tfidf, which can be bitsliced directly into whole number bitslices plus fractional bitslices (one for each binary digit to the right of the binary point-no need to shift!) using: MOD(INT(x/(2 k), 2), e. g. , a tfidf =3. 5 is 2 s 1 noun adv …noun … 2 2 1 2 3 DTPe Data Cube 1 0 D 0 0 0 Doc 0 . Auth… Date. . . Subj 1 …Subjm 1 1 1/2/13. . . 0 … 0 and 0 0 0 1 0 0 apple 0 0 1 0 0 0 1 . . . 2 3 0 . April 0 0 0 Doc T 1 P 1…T 1 P 7. . . T 9 P 1…T 9 P 7 1 1 … 0. . . 0 … 0 0 . are 0 0 0 2 0 . 3 0 2/2/15. . . 1 … 0 0 3/3/14. . . 1 … 0 0 … 0 . . . 1 … 1 . D o 0 1 1. 0 . 1 0 0 . 0 . . . 7 3 2 3 1 2 … 9 0 0 0 . 0 0 0 0 1 0 0 . . . 0 0 0 . 1 2 3 4 5 6 1 0 1 . . . 0 … 0 . c DTPe Document Table: 0 0 0 Classical Document Table: 1 0 0 . 2 Pos T 1 D 1 T 1 D 2 T 1 D 3. . . T 9 D 1…T 9 D 3 0 0 1 Pos T DTPe Position Table 0 0 2 1 0 Auth Doc. Tbl Dp. Tree. Set Date Subj 1 Subjm PT card D=k k=1, 2, 3 … 1 Pos DTPe k=1. . 3 PTCd 7 PDcard T=k k=1. . 9 … 1 T 1 k-2 1 7 TDcard P=k k=1. . 7 Term D. . . Term termfreq Data Cube adj s DTtf Doc. Term noun verb Term P 1 D 1 P 1 D 2 P 1 D 3. . . P 7 D 1…P 7 D 3 oc . . . 9 DTPe Tp. Tree. Set index (D, P) Positions 1 2 … Doc 3 1 1 P 1 D 1 Doc 2 1 noun 1 0 0 Doc 1 1 0 0 0 1 3 2 DTPe Term Table: Term P 1 D 1 P 1 D 2 P 1 D 3. . . P 7 D 1…P 7 D 3 7 0 … 0 . . . Term buy 1 … 1 Doc 3 Doc 2 1 0 0 1 Doc 1 0 DTPe in Pp. Tree. Set index (T, D)