10 -2 Volume of Prisms and Cylinders Preview

10 -2 Volume of Prisms and Cylinders Preview Warm Up California Standards Lesson Presentation Holt CA Course 1

10 -2 Volume of Prisms and Cylinders Warm Up Find the area of each figure described. Use 3. 14 for . 1. a triangle with a base of 6 feet and a height of 3 feet 9 ft 2 2. a circle with radius 5 in. 78. 5 in 2 Holt CA Course 1

10 -2 Volume of Prisms and Cylinders California Standards MG 2. 1 Use formulas routinely for finding the perimeter and area of basic twodimensional figures and the surface area and volume of basic three-dimensional figures, including rectangles, parallelograms, trapezoids, squares, triangles, circles, prisms, and cylinders. Also covered: MG 2. 4 Holt CA Course 1

10 -2 Volume of Prisms and Cylinders Vocabulary volume Holt CA Course 1

10 -2 Volume of Prisms and Cylinders The volume of a three-dimensional figure is the number of cubes it can hold. Each cube represents a unit of measure called a cubic unit. Holt CA Course 1

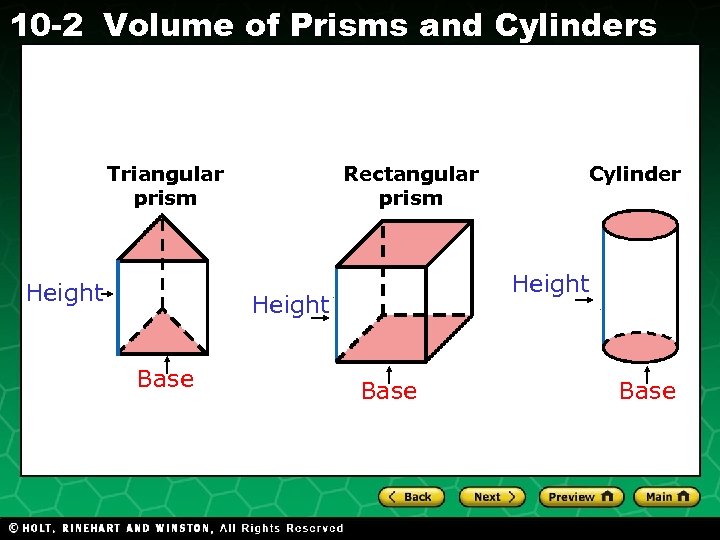10 -2 Volume of Prisms and Cylinders Rectangular prism Triangular prism Height Base Holt CA Course 1 Cylinder Base

10 -2 Volume of Prisms and Cylinders Holt CA Course 1

10 -2 Volume of Prisms and Cylinders Additional Example 1: Finding the Volume of Prisms and Cylinders Find the volume of each figure to the nearest tenth. A. B = 4 • 12 = 48 ft 2 The base is a rectangle. V = Bh Volume of a prism = 48 • 4 Substitute for B and h. = 192 ft 3 Multiply. Holt CA Course 1

10 -2 Volume of Prisms and Cylinders Additional Example 1: Finding the Volume of Prisms and Cylinders Find the volume of the figure to the nearest tenth. Use 3. 14 for . B. B = (42) = 16 in 2 V = Bh = 16 • 12 = 192 602. 9 in 3 Holt CA Course 1 The base is a circle. Volume of a cylinder Substitute for B and h. Multiply.

10 -2 Volume of Prisms and Cylinders Additional Example 1: Finding the Volume of Prisms and Cylinders Find the volume of the figure to the nearest tenth. Use 3. 14 for . C. B= 1 • 6 • 5 = 15 ft 2 The base is a 2 triangle. V = Bh 7 ft Volume of a prism Substitute for B and h. = 105 ft 3 Holt CA Course 1 = 15 • 7 Multiply.

10 -2 Volume of Prisms and Cylinders Check It Out! Example 1 Find the volume of the figure to the nearest tenth. Use 3. 14 for . A. 10 in. 6 in. 3 in. B = 6 • 3 = 18 in. 2 The base is a rectangle. V = Bh Volume of prism = 18 • 10 Substitute for B and h. = 180 in 3 Multiply. Holt CA Course 1

10 -2 Volume of Prisms and Cylinders Check It Out! Example 1 Find the volume of the figure to the nearest tenth. Use 3. 14 for . B. B = (82) 8 cm 15 cm = 64 cm 2 V = Bh The base is a circle. Volume of a cylinder Substitute for = (64 )(15) = 960 B and h. 3, 014. 4 cm 3 Holt CA Course 1 Multiply.

10 -2 Volume of Prisms and Cylinders Check It Out! Example 1 Find the volume of the figure to the nearest tenth. C. 10 ft 1 B= • 12 • 10 The base is a 2 triangle. = 60 ft 2 V = Bh 14 ft Volume of a prism = 60(14) 12 ft Holt CA Course 1 Substitute for B and h. = 840 ft 3 Multiply.

10 -2 Volume of Prisms and Cylinders Additional Example 2 A: Exploring the Effects of Changing Dimensions A juice box measures 3 in. by 2 in. by 4 in. Explain whether tripling only the length, width, or height of the box would triple the amount of juice the box holds. The original box has a volume of 24 in 3. You could triple the volume to 72 in 3 by tripling any one of the dimensions. So tripling the length, width, or height would triple the amount of juice the box holds. Holt CA Course 1

10 -2 Volume of Prisms and Cylinders Additional Example 2 B: Exploring the Effects of Changing Dimensions A juice can has a radius of 2 in. and a height of 5 in. Explain whether tripling only the height of the can would have the same effect on the volume as tripling the radius. By tripling the height, you would triple the volume. By tripling the radius, you would increase the volume to 9 times the original volume. Holt CA Course 1

10 -2 Volume of Prisms and Cylinders Check It Out! Example 2 A A box measures 5 in. by 3 in. by 7 in. Explain whether tripling only the length, width, or height of the box would triple the volume of the box. The original box has a volume of (5)(3)(7) = 105 cm 3. V = (15)(3)(7) = 315 cm 3 Tripling the length would triple the volume. Holt CA Course 1

10 -2 Volume of Prisms and Cylinders Check It Out! Example 2 A Continued The original box has a volume of (5)(3)(7) = 105 cm 3. V = (5)(3)(21) = 315 cm 3 Tripling the height would triple the volume. Holt CA Course 1

10 -2 Volume of Prisms and Cylinders Check It Out! Example 2 A Continued The original box has a volume of (5)(3)(7) = 105 cm 3. V = (5)(9)(7) = 315 cm 3 Tripling the width would triple the volume. Holt CA Course 1

10 -2 Volume of Prisms and Cylinders Check It Out! Example 2 B A cylinder measures 3 cm tall with a radius of 2 cm. Explain whether tripling only the radius or height of the cylinder would triple the amount of volume. The original cylinder has a volume of 4 • 3 = 12 cm 3. V = 36 • 3 = 108 cm 3 By tripling the radius, you would increase the volume nine times. Holt CA Course 1

10 -2 Volume of Prisms and Cylinders Check It Out! Example 2 B Continued The original cylinder has a volume of 4 • 3 = 12 cm 3. V = 4 • 9 = 36 cm 3 Tripling the height would triple the volume. Holt CA Course 1

10 -2 Volume of Prisms and Cylinders Additional Example 3: Music Application A drum company advertises a snare drum that is 4 inches high and 12 inches in diameter. Estimate the volume of the drum. d = 12, h = 4 r = d = 12 = 6 2 2 V = ( r 2)h = (3. 14)(6)2 Volume of a cylinder • 4 Use 3. 14 for . = (3. 14)(36)(4) = 452. 16 ≈ 452 The volume of the drum is approximately 452 in 3. Holt CA Course 1

10 -2 Volume of Prisms and Cylinders Check It Out! Example 3 A drum company advertises a bass drum that is 12 inches high and 28 inches in diameter. Estimate the volume of the drum. d = 28, h = 12 r = d = 28 = 14 2 2 V = ( r 2)h = (3. 14)(14)2 Volume of a cylinder • 12 Use 3. 14 for . = (3. 14)(196)(12) = 7385. 28 ≈ 7, 385 The volume of the drum is approximately 7, 385 in 3. Holt CA Course 1

10 -2 Volume of Prisms and Cylinders Additional Example 4: Finding the Volume of Composite Figures Find the volume of the barn. Volume of barn Volume of = rectangular + triangular prism 1 V = (40)(50)(15) + (40)(10)(50) 2 = 30, 000 + 10, 000 = 40, 000 ft 3 The volume of the barn is 40, 000 ft 3. Holt CA Course 1

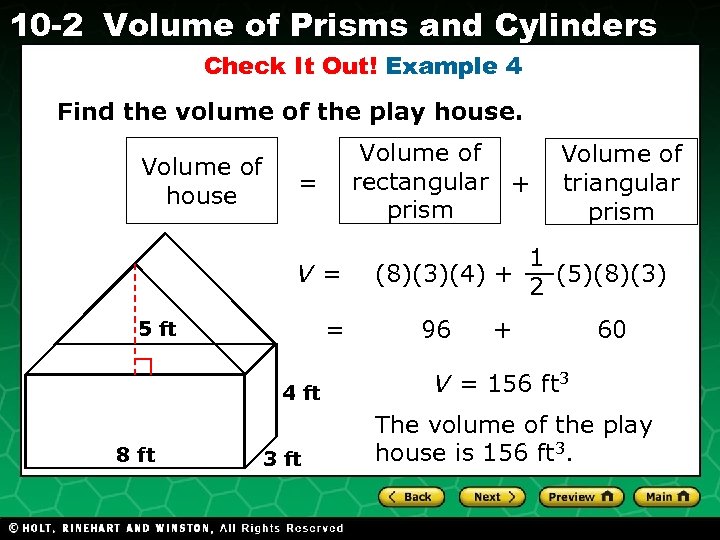10 -2 Volume of Prisms and Cylinders Check It Out! Example 4 Find the volume of the play house. Volume of house Volume of rectangular + prism = V= = 5 ft 4 ft 8 ft Holt CA Course 1 3 ft Volume of triangular prism 1 (8)(3)(4) + (5)(8)(3) 2 96 + 60 V = 156 ft 3 The volume of the play house is 156 ft 3.

10 -2 Volume of Prisms and Cylinders Lesson Quiz Find the volume of each figure to the nearest tenth. Use 3. 14 for . 10 in. 12 in. 2. 12 in. 3. 10. 7 in. 2 in. 15 in. 8. 5 in. 3 in. 942 in 3 160. 5 in 3 306 in 3 4. Explain whether doubling the radius of the cylinder above will double the volume. No; the volume would be quadrupled because you have to use the square of the radius to find the volume. Holt CA Course 1