d8d0e66f484d327f516e2fadd01572a0.ppt
- Количество слайдов: 19

10. 1 – Counting by Systematic Listing One-Part Tasks The results for simple, one-part tasks can often be listed easily. Tossing a fair coin: Heads or tails Rolling a single fair die 1, 2, 3, 4, 5, 6 Consider a club N with four members: N = {Mike, Adam, Ted, Helen} or N = {M, A, T, H} In how many ways can this group select a president? There are four possible results: M, A, T, and H.

10. 1 – Counting by Systematic Listing Product Tables for Two-Part Tasks Determine the number of two-digit numbers that can be written using the digits from the set {2, 4, 6}. The task consists of two parts: 1. Choose a first digit 2. Choose a second digit The results for a two-part task can be pictured in a product table. First Digit 2 4 6 2 22 42 62 Second Digit 4 24 44 64 6 26 46 66 9 possible numbers
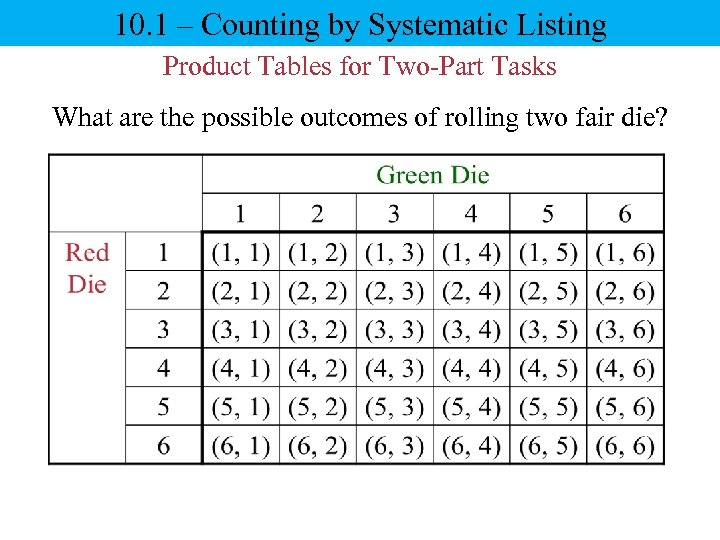
10. 1 – Counting by Systematic Listing Product Tables for Two-Part Tasks What are the possible outcomes of rolling two fair die?
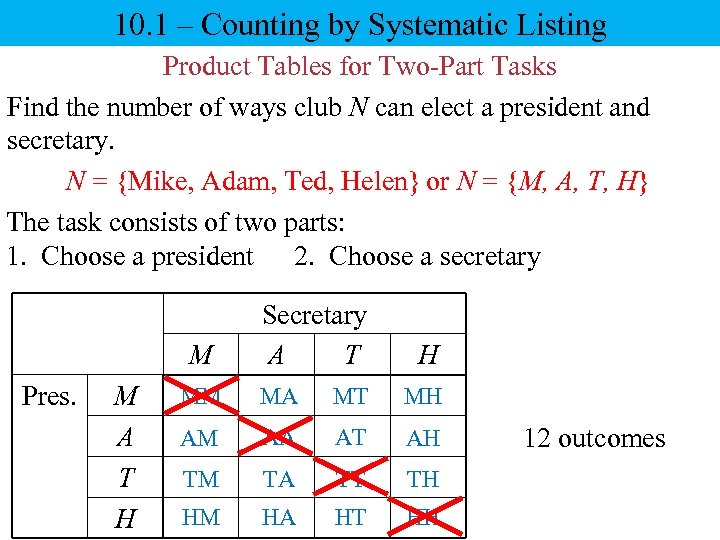
10. 1 – Counting by Systematic Listing Product Tables for Two-Part Tasks Find the number of ways club N can elect a president and secretary. N = {Mike, Adam, Ted, Helen} or N = {M, A, T, H} The task consists of two parts: 1. Choose a president 2. Choose a secretary M Pres. M A T H Secretary A T H MM MA MT MH AM AA AT AH TM TA TT TH HM HA HT HH 12 outcomes
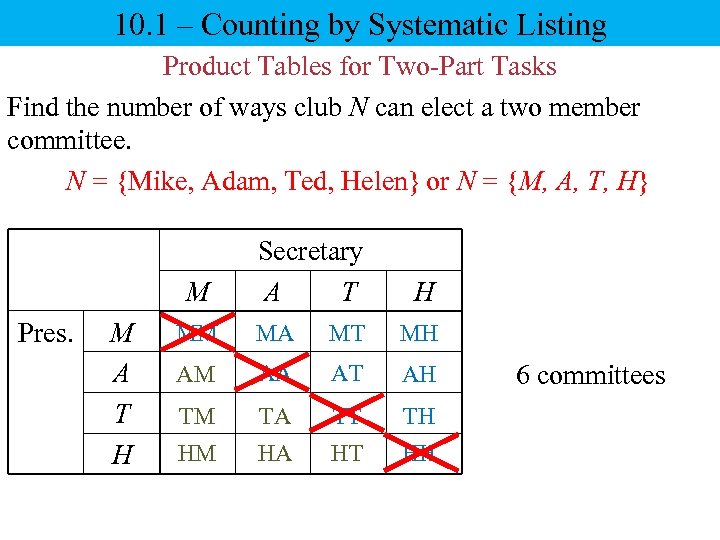
10. 1 – Counting by Systematic Listing Product Tables for Two-Part Tasks Find the number of ways club N can elect a two member committee. N = {Mike, Adam, Ted, Helen} or N = {M, A, T, H} M Pres. M A T H Secretary A T H MM MA MT MH AM AA AT AH TM TA TT TH HM HA HT HH 6 committees

10. 1 – Counting by Systematic Listing Tree Diagrams for Multiple-Part Tasks A task that has more than two parts is not easy to analyze with a product table. Another helpful device is a tree diagram. Find the number of three digit numbers that can be written using the digits from the set {2, 4, 6} assuming repeated digits are not allowed. A product table will not work for more than two digits. Generating a list could be time consuming and disorganized.
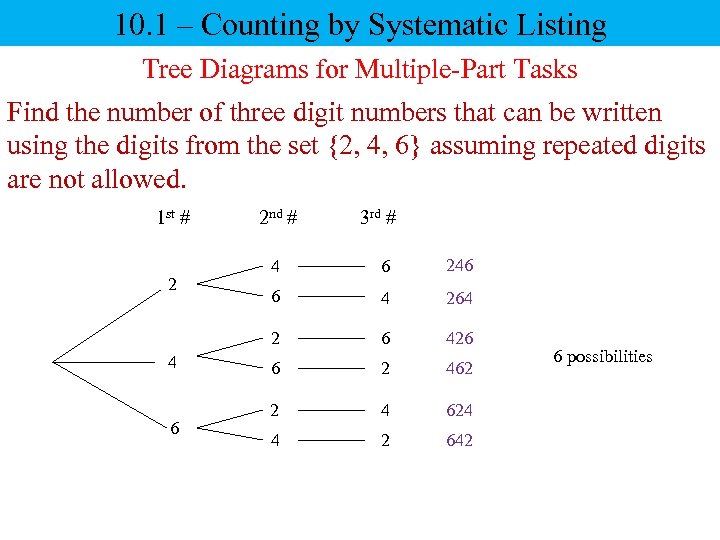
10. 1 – Counting by Systematic Listing Tree Diagrams for Multiple-Part Tasks Find the number of three digit numbers that can be written using the digits from the set {2, 4, 6} assuming repeated digits are not allowed. 1 st # 2 nd # 3 rd # 4 6 6 246 6 4 264 2 2 4 6 426 6 2 462 2 4 624 4 2 642 6 possibilities

10. 1 – Counting by Systematic Listing Other Systematic Listing Methods There additional systematic ways to produce complete listings of possible results besides product tables and tree diagrams. How many triangles (of any size) are in the figure below? D E C F A B One systematic approach is begin with A, and proceed in alphabetical order to write all 3 -letter combinations (like ABC, ABD, …), then cross out ones that are not triangles and those that repeat. Another approach is to “chunk” the figure to smaller, more manageable figures. There are 12 triangles.

10. 2 – Using the Fundamental Counting Principle Uniformity Criterion for Multiple-Part Tasks: A multiple part task is said to satisfy the uniformity criterion if the number of choices for any particular part is the same no matter which choices were selected for previous parts. Uniformity exists: Find the number of three letter combinations that can be written using the letters from the set {a, b, c} assuming repeated letters are not allowed. 2 dimes and one six-sided die numbered from 1 to 6 are tossed. Generate a list of the possible outcomes by drawing a tree diagram. Uniformity does not exists: A computer printer allows for optional settings with a panel of five on-off switches. Set up a tree diagram that will show many setting are possible so that no two adjacent switches can be on?

10. 2 – Using the Fundamental Counting Principle Uniformity Find the number of three letter combinations that can be written using the letters from the set {a, b, c} assuming repeated letters are not allowed. 1 st letter b c 3 rd letter b c abc c b acb a a 2 nd letter c bac c a bca a b cab b a cba 6 possibilities
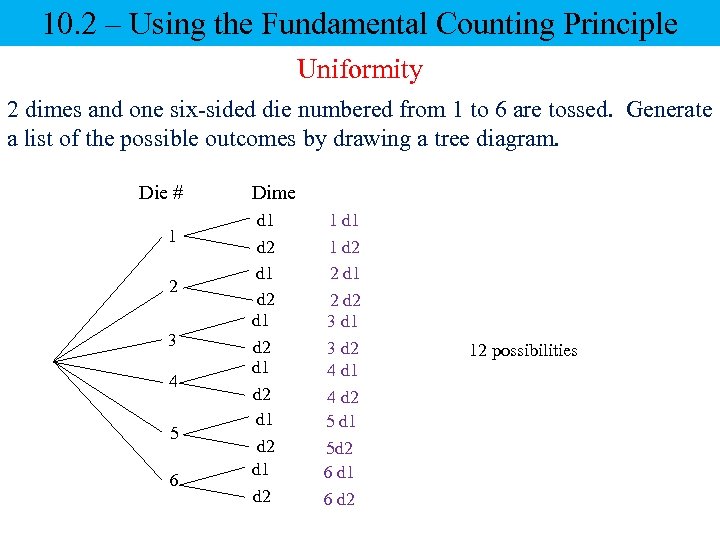
10. 2 – Using the Fundamental Counting Principle Uniformity 2 dimes and one six-sided die numbered from 1 to 6 are tossed. Generate a list of the possible outcomes by drawing a tree diagram. Die # 1 2 3 4 5 6 Dime d 1 d 2 d 1 d 2 1 d 1 1 d 2 2 d 1 2 d 2 3 d 1 3 d 2 4 d 1 4 d 2 5 d 1 5 d 2 6 d 1 6 d 2 12 possibilities
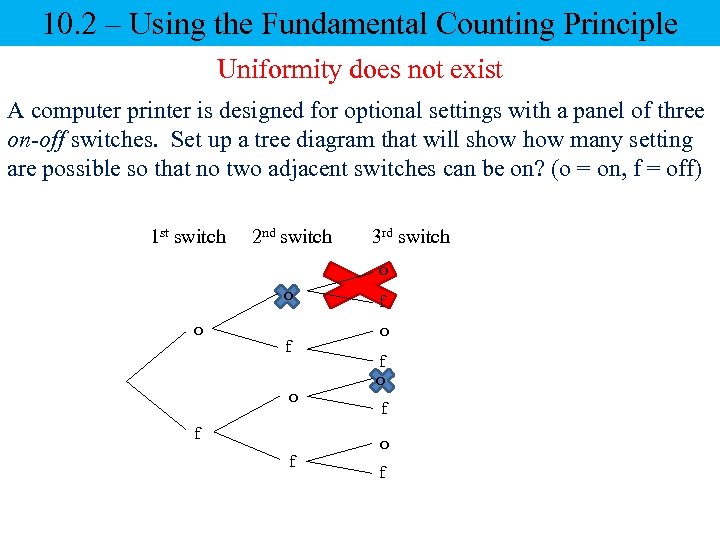
10. 2 – Using the Fundamental Counting Principle Uniformity does not exist A computer printer is designed for optional settings with a panel of three on-off switches. Set up a tree diagram that will show many setting are possible so that no two adjacent switches can be on? (o = on, f = off) 1 st switch 2 nd switch 3 rd switch o o o f f f o f o f

10. 2 – Using the Fundamental Counting Principle The principle which states that all possible outcomes in a sample space can be found by multiplying the number of ways each event can occur. Example: At a firehouse fundraiser dinner, one can choose from 2 proteins (beef and fish), 4 vegetables (beans, broccoli, carrots, and corn), and 2 breads (rolls and biscuits). How many different protein-vegetable-bread selections can she make for dinner? Proteins 2 Vegetables 4 Breads 16 possible selections 2 =

10. 2 – Using the Fundamental Counting Principle Example At the local sub shop, customers have a choice of the following: 3 breads (white, wheat, rye), 4 meats (turkey, ham, chicken, bologna), 6 condiments (none, brown mustard, spicy mustard, honey mustard, ketchup, mayo), and 3 cheeses (none, Swiss, American). How many different sandwiches are possible? Breads 3 Meats 4 Condiments Cheeses 6 3 = 216 possible sandwiches

10. 2 – Using the Fundamental Counting Principle Example: Consider the set of digits: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}. (a) How many two digit numbers can be formed if repetitions are allowed? 1 st digit 9 2 nd digit 10 = 90 (b) How many two digit numbers can be formed if no repetitions are allowed? 1 st digit 9 2 nd digit 9 = 81 (c) How many three digit numbers can be formed if no repetitions are allowed? 1 st digit 9 2 nd digit 9 3 rd digit 8 = 648

10. 2 – Using the Fundamental Counting Principle Example: (a) How many five-digit codes are possible if the first two digits are letters and the last three digits are numerical? 1 st digit 26 2 nd digit 3 rd digit 4 th digit 10 26 676000 possible five-digit codes 5 th digit 10 (a) How many five-digit codes are possible if the first two digits are letters and the last three digits are numerical and repeats are not permitted? 1 st digit 26 2 nd digit 3 rd digit 4 th digit 10 9 25 468000 possible five-digit codes 5 th digit 8

10. 2 – Using the Fundamental Counting Principle Factorials For any counting number n, the product of all counting numbers from n down through 1 is called n factorial, and is denoted n!. For any counting number n, the quantity n factorial is calculated by: n! = n(n – 1)(n – 2)…(2)(1). Definition of Zero Factorial: 0! = 1 Examples: a) 4! b) (4 – 1)! 4 3 2 1 24 3! 3 2 1 6 c) = 5 4 = 20

10. 2 – Using the Fundamental Counting Principle Arrangements of Objects Factorials are used when finding the total number of ways to arrange a given number of distinct objects. The total number of different ways to arrange n distinct objects is n!. Example: How many ways can you line up 6 different books on a shelf? 6 5 4 3 720 possible arrangements 2 1

10. 2 – Using the Fundamental Counting Principle Arrangements of n Objects Containing Look-Alikes The number of distinguishable arrangements of n objects, where one or more subsets consist of look-alikes (say n 1 are of one kind, n 2 are of another kind, …, and nk are of yet another kind), is given by Example: Determine the number of distinguishable arrangements of the letters of the word INITIALLY. 9 letters 9! 3! 2! with 3 I’s and 2 L’s 30240 possible arrangements
d8d0e66f484d327f516e2fadd01572a0.ppt