48b94a46ca8d2686b29d56928c2d700b.ppt
- Количество слайдов: 39
 1 Želimir Kurtanjek Computer aided modelling, design and development of processes in food industry Faculty of Food Technology and Biotechnology University of Zagreb Pierottijeva 6, 10000 Zagreb, CROATIA zkurt@pbf. hr
1 Želimir Kurtanjek Computer aided modelling, design and development of processes in food industry Faculty of Food Technology and Biotechnology University of Zagreb Pierottijeva 6, 10000 Zagreb, CROATIA zkurt@pbf. hr
 SCOPE 1. Objectives for computer aided process design and development 2. Information systems in industry 3. Computer aided modelling techniques and software 4. Examples 3. Conclusions 2
SCOPE 1. Objectives for computer aided process design and development 2. Information systems in industry 3. Computer aided modelling techniques and software 4. Examples 3. Conclusions 2
 Limitations for investments in food production 1. market demand 2. human resources (knowledge) 3. material resources 4. financial resources 5. environment impact 6. technology 7. product quality 8. product diversification Most of the limitations can be analysed and solutions optimised by use of computer models 3
Limitations for investments in food production 1. market demand 2. human resources (knowledge) 3. material resources 4. financial resources 5. environment impact 6. technology 7. product quality 8. product diversification Most of the limitations can be analysed and solutions optimised by use of computer models 3
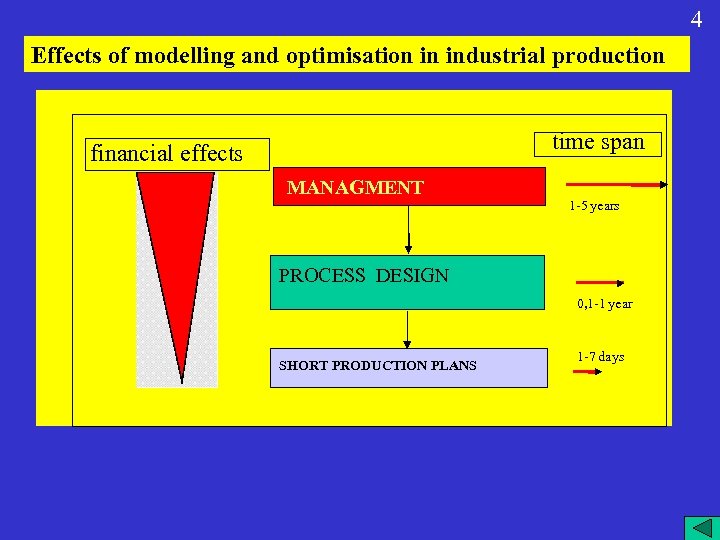 4 Effects of modelling and optimisation in industrial production time span financial effects MANAGMENT 1 -5 years PROCESS DESIGN 0, 1 -1 year SHORT PRODUCTION PLANS 1 -7 days
4 Effects of modelling and optimisation in industrial production time span financial effects MANAGMENT 1 -5 years PROCESS DESIGN 0, 1 -1 year SHORT PRODUCTION PLANS 1 -7 days
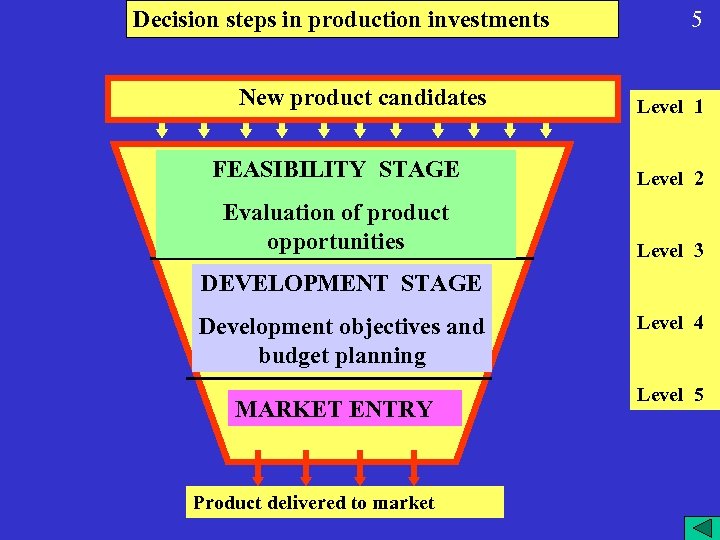 Decision steps in production investments New product candidates 5 Level 1 FEASIBILITY STAGE Level 2 Evaluation of product opportunities Level 3 DEVELOPMENT STAGE Development objectives and budget planning MARKET ENTRY Product delivered to market Level 4 Level 5
Decision steps in production investments New product candidates 5 Level 1 FEASIBILITY STAGE Level 2 Evaluation of product opportunities Level 3 DEVELOPMENT STAGE Development objectives and budget planning MARKET ENTRY Product delivered to market Level 4 Level 5
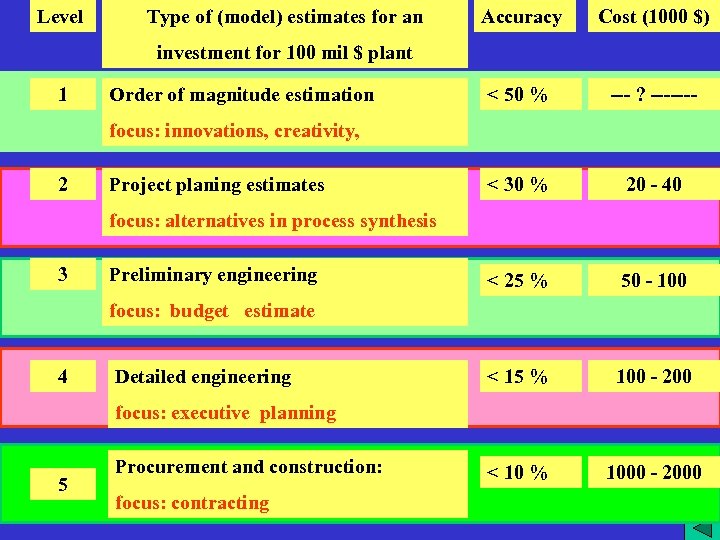 Level Type of (model) estimates for an Accuracy Cost (1000 6 $) < 50 % --- ? ------- < 30 % 20 - 40 < 25 % 50 - 100 < 15 % 100 - 200 < 10 % 1000 - 2000 investment for 100 mil $ plant 1 Order of magnitude estimation focus: innovations, creativity, 2 Project planing estimates focus: alternatives in process synthesis 3 Preliminary engineering focus: budget estimate 4 Detailed engineering focus: executive planning 5 Procurement and construction: focus: contracting
Level Type of (model) estimates for an Accuracy Cost (1000 6 $) < 50 % --- ? ------- < 30 % 20 - 40 < 25 % 50 - 100 < 15 % 100 - 200 < 10 % 1000 - 2000 investment for 100 mil $ plant 1 Order of magnitude estimation focus: innovations, creativity, 2 Project planing estimates focus: alternatives in process synthesis 3 Preliminary engineering focus: budget estimate 4 Detailed engineering focus: executive planning 5 Procurement and construction: focus: contracting
 CHARACTERISTICS OF 7 MODEL DEVELOPMENT 1. APPLICATION OF SYSTEMS VIEW 2. INTEGRATION OF KNOWLEDGE : thermodynamics, transport phenomena, biochemistry, mathematics, computer science 3. APPLICATION OF AI ALGORITHMS FOR AUTOMATED INFORMATION BASED MODELING fuzzy logic modelling, neural networks
CHARACTERISTICS OF 7 MODEL DEVELOPMENT 1. APPLICATION OF SYSTEMS VIEW 2. INTEGRATION OF KNOWLEDGE : thermodynamics, transport phenomena, biochemistry, mathematics, computer science 3. APPLICATION OF AI ALGORITHMS FOR AUTOMATED INFORMATION BASED MODELING fuzzy logic modelling, neural networks
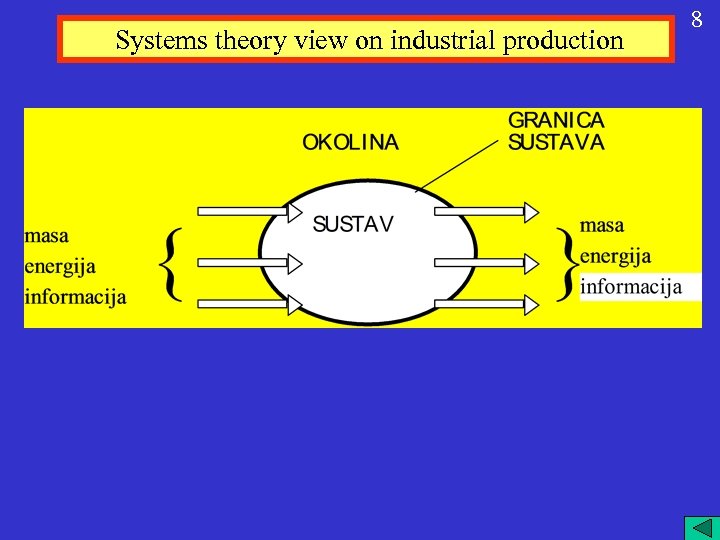 Systems theory view on industrial production 8
Systems theory view on industrial production 8
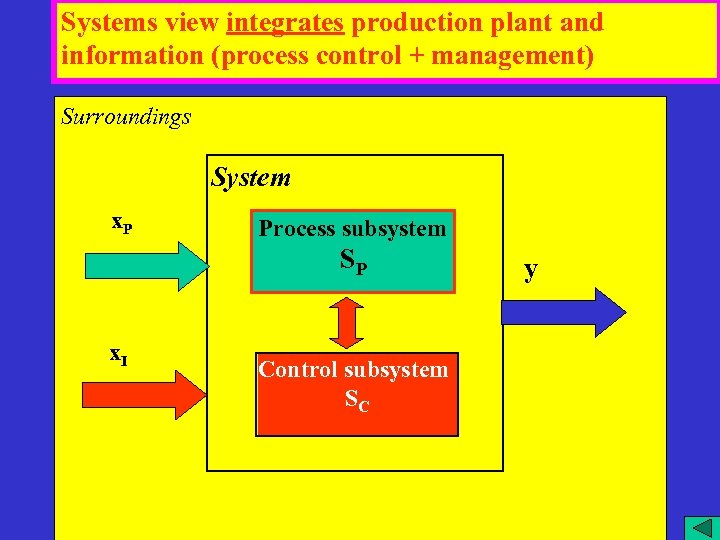 Systems view integrates production plant and information (process control + management) Surroundings System x. P Process subsystem SP x. I Control subsystem SC y 9
Systems view integrates production plant and information (process control + management) Surroundings System x. P Process subsystem SP x. I Control subsystem SC y 9
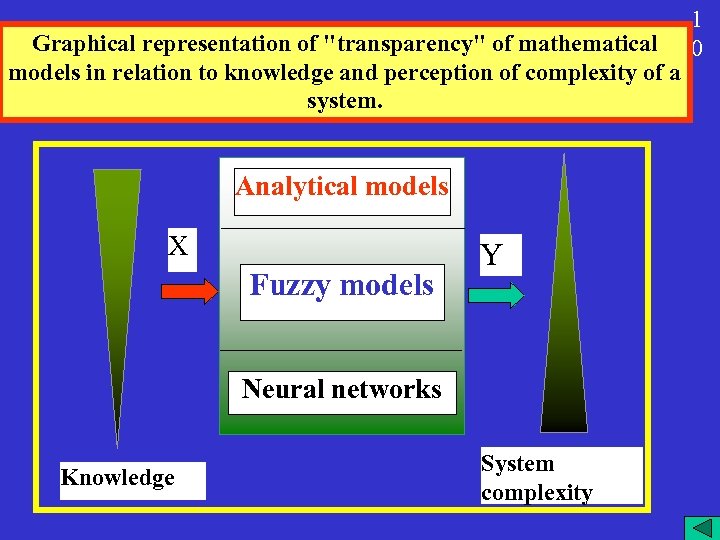 Graphical representation of "transparency" of mathematical models in relation to knowledge and perception of complexity of a system. Analytical models X Fuzzy models Y Neural networks Knowledge System complexity 1 0
Graphical representation of "transparency" of mathematical models in relation to knowledge and perception of complexity of a system. Analytical models X Fuzzy models Y Neural networks Knowledge System complexity 1 0
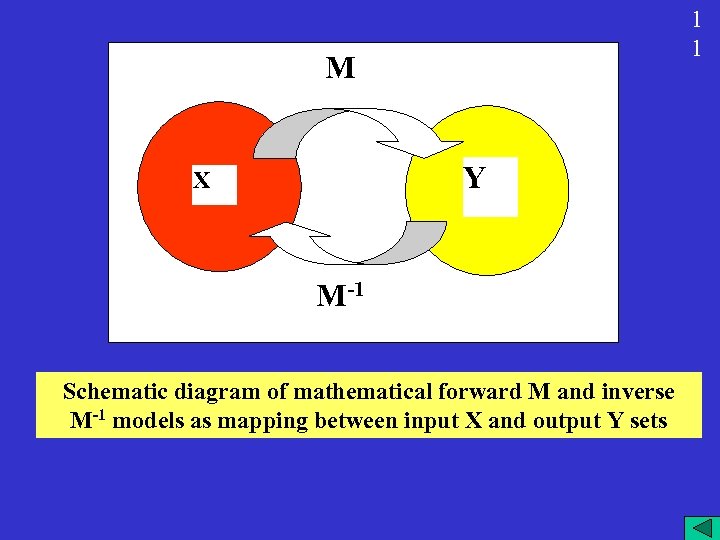 1 1 M Y X M-1 Schematic diagram of mathematical forward M and inverse M-1 models as mapping between input X and output Y sets
1 1 M Y X M-1 Schematic diagram of mathematical forward M and inverse M-1 models as mapping between input X and output Y sets
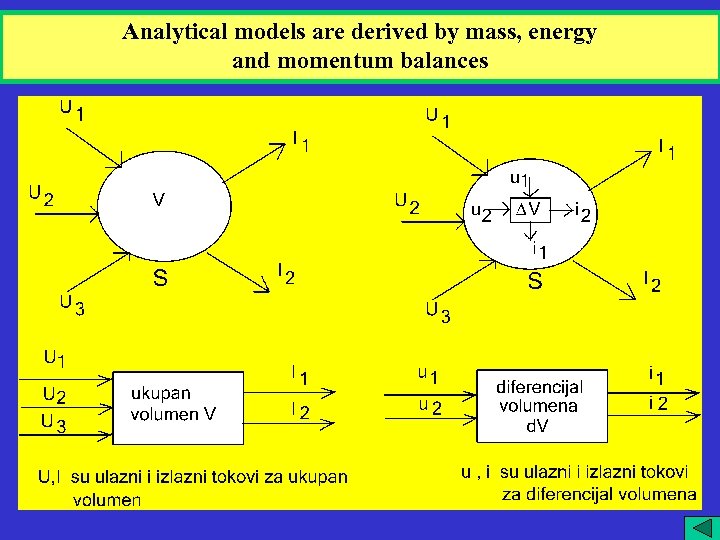 Analytical models are derived by mass, energy and momentum balances 1 2
Analytical models are derived by mass, energy and momentum balances 1 2
 General structure of a process dynamic model in a finite dimensions state space 1 3
General structure of a process dynamic model in a finite dimensions state space 1 3
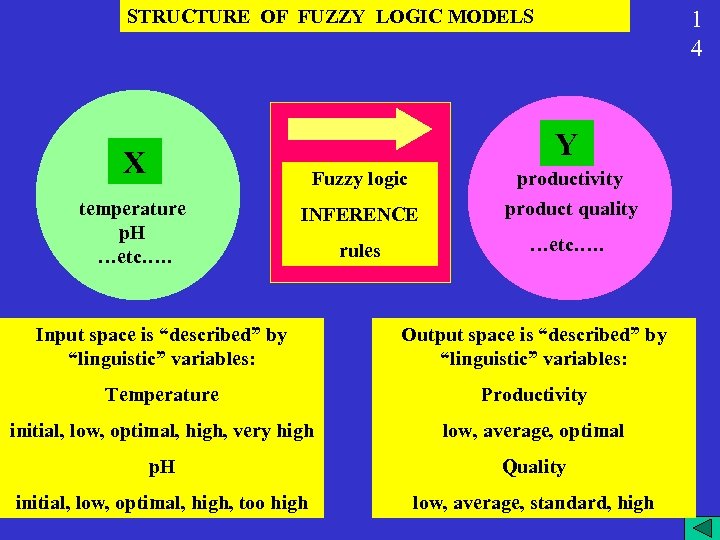 STRUCTURE OF FUZZY LOGIC MODELS 1 4 Y X Fuzzy logic temperature p. H …etc. …. INFERENCE productivity product quality rules …etc. …. Input space is “described” by “linguistic” variables: Output space is “described” by “linguistic” variables: Temperature Productivity initial, low, optimal, high, very high low, average, optimal p. H Quality initial, low, optimal, high, too high low, average, standard, high
STRUCTURE OF FUZZY LOGIC MODELS 1 4 Y X Fuzzy logic temperature p. H …etc. …. INFERENCE productivity product quality rules …etc. …. Input space is “described” by “linguistic” variables: Output space is “described” by “linguistic” variables: Temperature Productivity initial, low, optimal, high, very high low, average, optimal p. H Quality initial, low, optimal, high, too high low, average, standard, high
 Fuzzy sets are associated with linguistic variables Fuzzy sets are defined by membership functions very high optimal low initial high 1 5
Fuzzy sets are associated with linguistic variables Fuzzy sets are defined by membership functions very high optimal low initial high 1 5
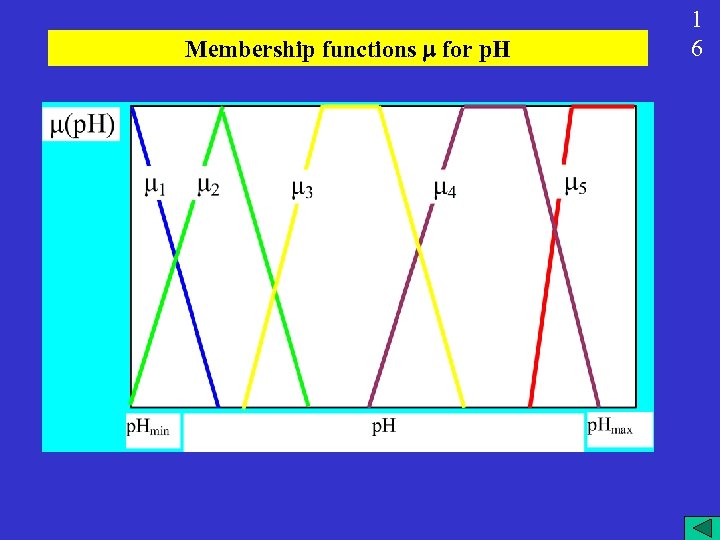 Membership functions for p. H 1 6
Membership functions for p. H 1 6
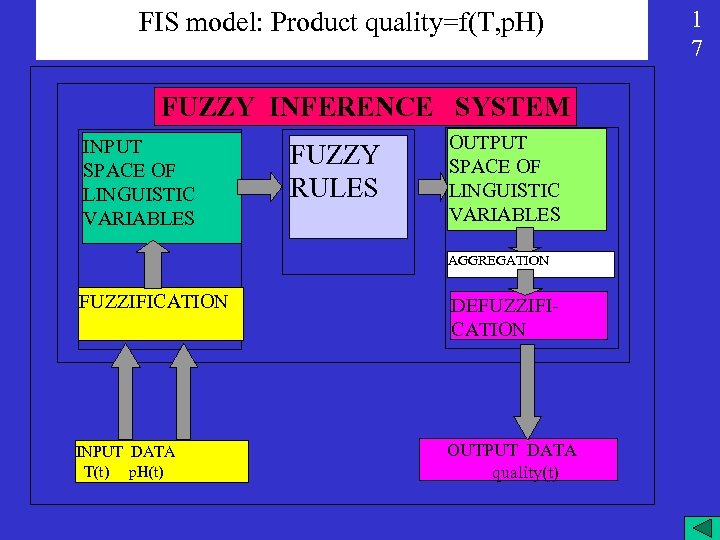 FIS model: Product quality=f(T, p. H) FUZZY INFERENCE SYSTEM INPUT SPACE OF LINGUISTIC VARIABLES FUZZY RULES OUTPUT SPACE OF LINGUISTIC VARIABLES AGGREGATION FUZZIFICATION DEFUZZIFICATION INPUT DATA T(t) p. H(t) OUTPUT DATA quality(t) 1 7
FIS model: Product quality=f(T, p. H) FUZZY INFERENCE SYSTEM INPUT SPACE OF LINGUISTIC VARIABLES FUZZY RULES OUTPUT SPACE OF LINGUISTIC VARIABLES AGGREGATION FUZZIFICATION DEFUZZIFICATION INPUT DATA T(t) p. H(t) OUTPUT DATA quality(t) 1 7
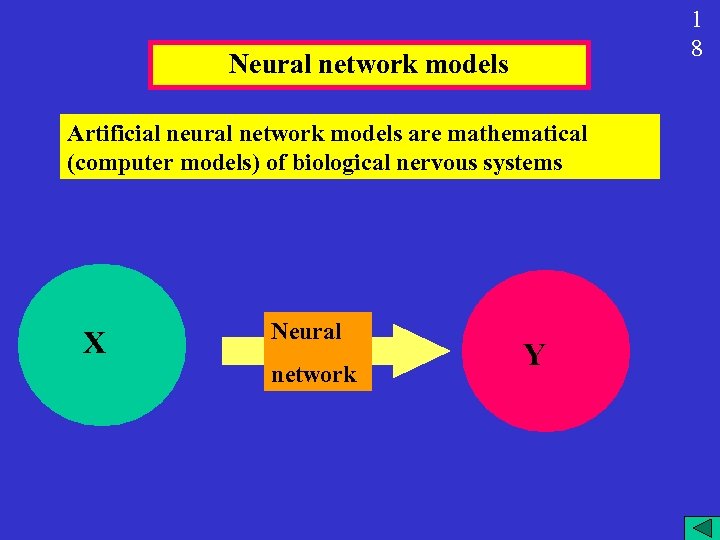 1 8 Neural network models Artificial neural network models are mathematical (computer models) of biological nervous systems X Neural network Y
1 8 Neural network models Artificial neural network models are mathematical (computer models) of biological nervous systems X Neural network Y
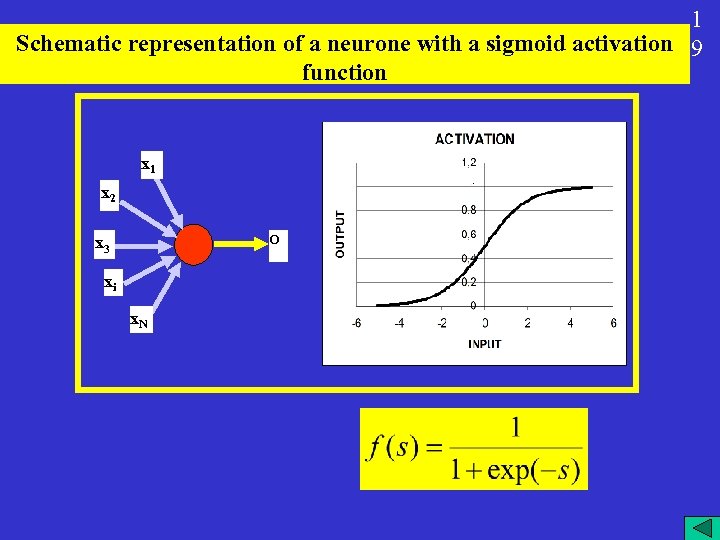 1 Schematic representation of a neurone with a sigmoid activation 9 function x 1 x 2 O x 3 xi x. N
1 Schematic representation of a neurone with a sigmoid activation 9 function x 1 x 2 O x 3 xi x. N
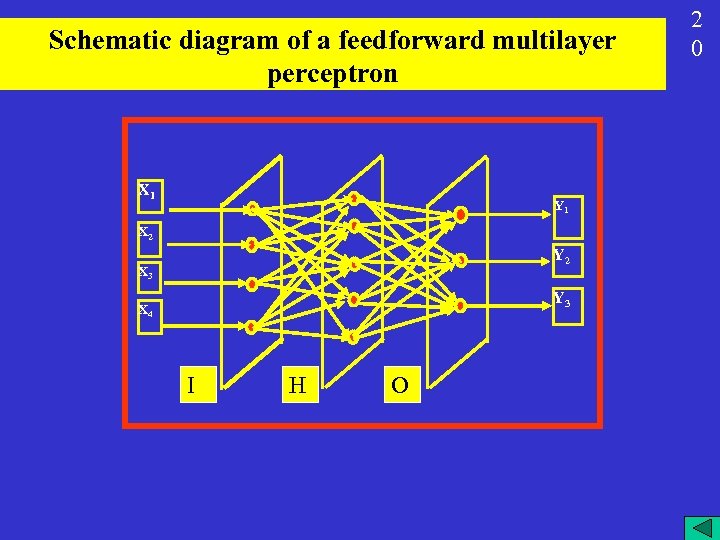 Schematic diagram of a feedforward multilayer perceptron X 1 Y 1 X 2 Y 2 X 3 Y 3 X 4 I H O 2 0
Schematic diagram of a feedforward multilayer perceptron X 1 Y 1 X 2 Y 2 X 3 Y 3 X 4 I H O 2 0
 Applications Fuzzy logic models Modelling human knowledge (reasoning) Process regulation Product recipes Product quality assurance Neural networks Modelling of complex systems Control of fermentation Image analysis Electronic noses Process automation, Robotisation 2 1
Applications Fuzzy logic models Modelling human knowledge (reasoning) Process regulation Product recipes Product quality assurance Neural networks Modelling of complex systems Control of fermentation Image analysis Electronic noses Process automation, Robotisation 2 1
 COMPUTER AIDED PROCESS SYNTHESIS INPUT OTPUT MODELS OF UNIT OPERATIONS + PROPERTY DATA + NUMERICAL METHODS FOR BALANCE SOLVING RIGOROUS: THERMODYNAMIC MODELS OF REAL SYTEMS PRELIMINARY: THERMODYNAMICS OF IDEAL SYSTEMS 2 2
COMPUTER AIDED PROCESS SYNTHESIS INPUT OTPUT MODELS OF UNIT OPERATIONS + PROPERTY DATA + NUMERICAL METHODS FOR BALANCE SOLVING RIGOROUS: THERMODYNAMIC MODELS OF REAL SYTEMS PRELIMINARY: THERMODYNAMICS OF IDEAL SYSTEMS 2 2
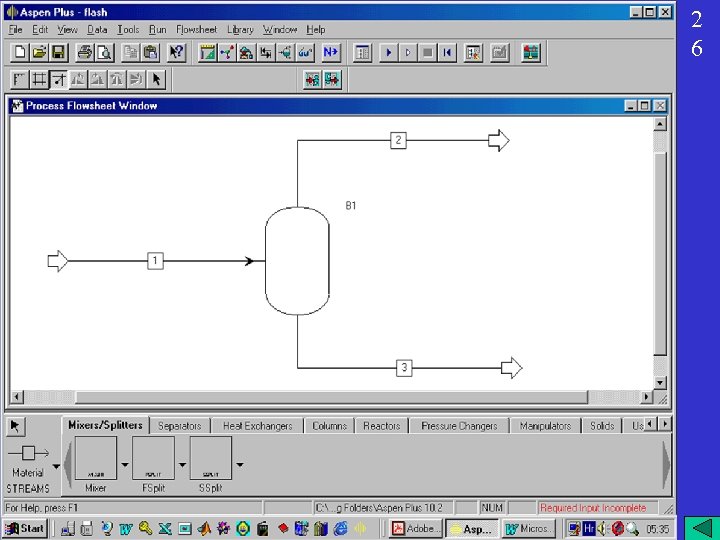
 SOFTWARE FOR COMPUTER AIDED PROCESS DESIGN Rigorous design ASPEN PLUS Feasibility design INTELLIGEN, INC. BIO DESIGNER ENVIRONMENT DESIGNER SUPER DESIGNER 2 3
SOFTWARE FOR COMPUTER AIDED PROCESS DESIGN Rigorous design ASPEN PLUS Feasibility design INTELLIGEN, INC. BIO DESIGNER ENVIRONMENT DESIGNER SUPER DESIGNER 2 3
 ASPEN PLUS 2 4 Aspen Plus makes it easy to build and run a process simulation model by providing a comprehensive system of online prompts, hypertext help, and expert system guidance at every step. In many cases, user is able to develop an Aspen Plus process simulation model without referring to printed manuals. Process simulation to predict the behavior of a process by using basic engineering relationships, such as mass and energy balances, and phase and chemical equilibrium. Given reliable thermodynamic data, realistic operating conditions, and rigorous equipment models can simulate actual plant behavior. Process simulation enables to run many cases, conduct "what if"analyses, and perform sensitivity studies and optimization runs. With simulation, design of better plants and increase profitability in existing plants is possible. Process simulation is useful throughout the entire lifecycle of a process, fromresearch and development through process design to production.
ASPEN PLUS 2 4 Aspen Plus makes it easy to build and run a process simulation model by providing a comprehensive system of online prompts, hypertext help, and expert system guidance at every step. In many cases, user is able to develop an Aspen Plus process simulation model without referring to printed manuals. Process simulation to predict the behavior of a process by using basic engineering relationships, such as mass and energy balances, and phase and chemical equilibrium. Given reliable thermodynamic data, realistic operating conditions, and rigorous equipment models can simulate actual plant behavior. Process simulation enables to run many cases, conduct "what if"analyses, and perform sensitivity studies and optimization runs. With simulation, design of better plants and increase profitability in existing plants is possible. Process simulation is useful throughout the entire lifecycle of a process, fromresearch and development through process design to production.
 2 5
2 5
 2 6
2 6
 2 7
2 7
 2 8
2 8
 2 9 INLET STREAM: ID 1 OUTLET VAPOR STREAM: ID 2 OUTLET LIQUID STREAM: ID 3 PROPERTY OPTION SET: NRTL RENON (NRTL) / IDEAL GAS *** MASS AND ENERGY BALANCE *** IN OUT RELATIVE DIFF. TOTAL BALANCE MOLE(KMOL/HR ) 50. 000000 E+00 MASS(KG/HR ) 1251. 44 0. 181690 E-15 ENTHALPY(CAL/SEC ) -853878. -853880. 0. 182470 E-05
2 9 INLET STREAM: ID 1 OUTLET VAPOR STREAM: ID 2 OUTLET LIQUID STREAM: ID 3 PROPERTY OPTION SET: NRTL RENON (NRTL) / IDEAL GAS *** MASS AND ENERGY BALANCE *** IN OUT RELATIVE DIFF. TOTAL BALANCE MOLE(KMOL/HR ) 50. 000000 E+00 MASS(KG/HR ) 1251. 44 0. 181690 E-15 ENTHALPY(CAL/SEC ) -853878. -853880. 0. 182470 E-05
 Super. Pro Designer® A Computing Environment for Designing and Optimizing Integrated Specialty Chemicals, Biochemical, Pharmaceutical, Food, Packaging, Water Purification, Wastewater Treatment and Air Pollution Control Processes INTELLIGEN, INC. - 2326 Morse Avenue - Scotch Plains, NJ 07076 - USA 3 0
Super. Pro Designer® A Computing Environment for Designing and Optimizing Integrated Specialty Chemicals, Biochemical, Pharmaceutical, Food, Packaging, Water Purification, Wastewater Treatment and Air Pollution Control Processes INTELLIGEN, INC. - 2326 Morse Avenue - Scotch Plains, NJ 07076 - USA 3 0
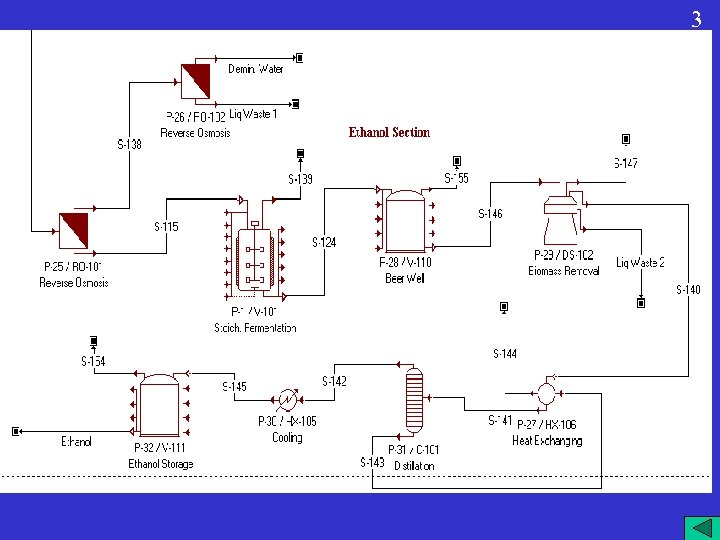
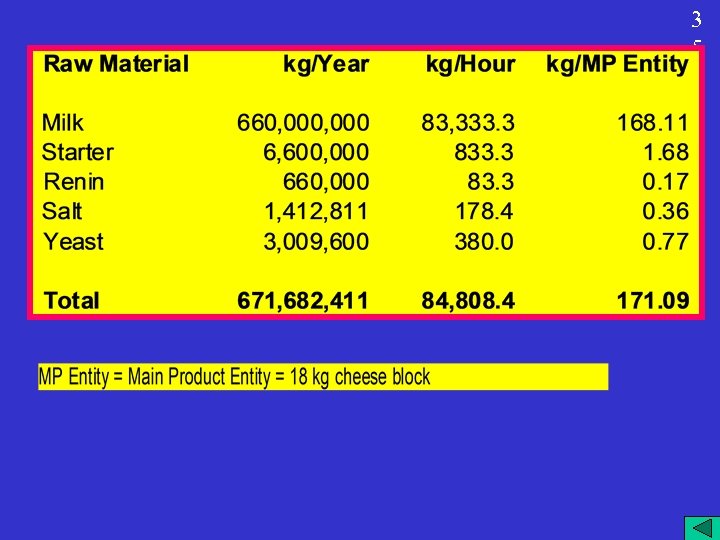
 Integrated Cheese Plant 3 1 This example deals with an integrated milk processing plant that produces cheese, butter, whey protein concentrate (WPC), and food-grade ethanol. The plant operates around the clock for 330 days a year and on a daily basis processes 2, 000 metric tons of milk (83, 333 kg/h) and produces 214 tons of cheese, 9 tons of butter, 211 tons of WPC, and 28 tons of ethanol. The plant consists of four sections: Cheese Making, Butter Making, WPC Making, and Ethanol Making.
Integrated Cheese Plant 3 1 This example deals with an integrated milk processing plant that produces cheese, butter, whey protein concentrate (WPC), and food-grade ethanol. The plant operates around the clock for 330 days a year and on a daily basis processes 2, 000 metric tons of milk (83, 333 kg/h) and produces 214 tons of cheese, 9 tons of butter, 211 tons of WPC, and 28 tons of ethanol. The plant consists of four sections: Cheese Making, Butter Making, WPC Making, and Ethanol Making.
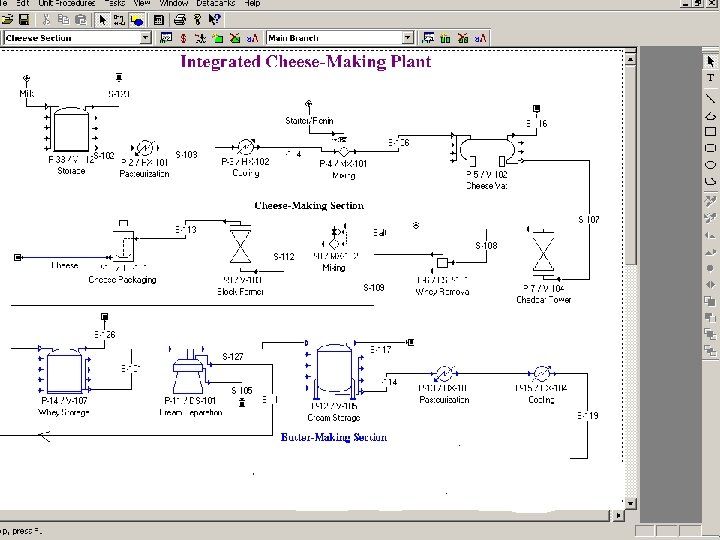 3 2
3 2
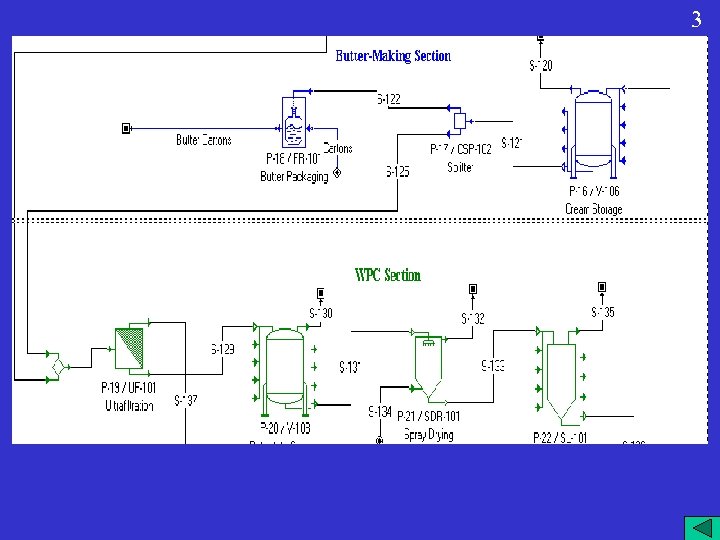 3 3
3 3
 3 4
3 4
 3 5
3 5
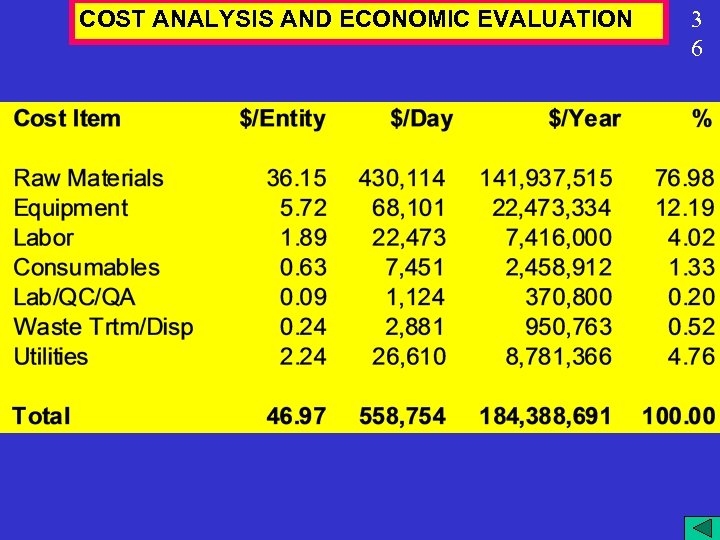 COST ANALYSIS AND ECONOMIC EVALUATION 3 6
COST ANALYSIS AND ECONOMIC EVALUATION 3 6
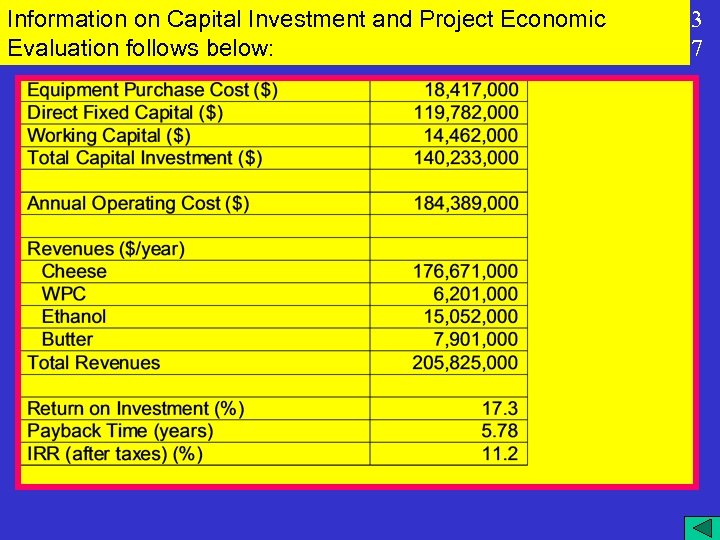 Information on Capital Investment and Project Economic Evaluation follows below: 3 7
Information on Capital Investment and Project Economic Evaluation follows below: 3 7
 CONCLUSIONS 1. Mathematical modeling is an integrated part of process development, design and control in food industry 2. Analytical mathematical models based on mass and energy balances for unit operations is the principal tool in process design and optimal synthesis. 3. Mathematical models based on informatics (fuzzy logic and neural networks) are applied for process control (robotisation, computer vision, expert systems. . ) 4. Use of computer software for design and process control is essential. 3 8
CONCLUSIONS 1. Mathematical modeling is an integrated part of process development, design and control in food industry 2. Analytical mathematical models based on mass and energy balances for unit operations is the principal tool in process design and optimal synthesis. 3. Mathematical models based on informatics (fuzzy logic and neural networks) are applied for process control (robotisation, computer vision, expert systems. . ) 4. Use of computer software for design and process control is essential. 3 8
 LITERATURE 1. Ž. Kurtanjek, “Matematičko modeliranje i vođenje procesa”, Lecture notes, Faculty of Food Technology and Biotechnology, University of Zagreb, 1995. 2. Ž. Kurtanjek, “Matematičko modeliranje procesa u prehrambenoj industriji”, Lecture notes, Faculty of Food Technology, University of Osijek, 2000. 3. “Aspen Plus 10. 1”, Manual, Aspen Technology, Inc. , Boston, MA, USA, 2000. 4. “Super Pro Design v. 4. 5”, Manual, INTELLIGEN, INC. , 2001. 3 9
LITERATURE 1. Ž. Kurtanjek, “Matematičko modeliranje i vođenje procesa”, Lecture notes, Faculty of Food Technology and Biotechnology, University of Zagreb, 1995. 2. Ž. Kurtanjek, “Matematičko modeliranje procesa u prehrambenoj industriji”, Lecture notes, Faculty of Food Technology, University of Osijek, 2000. 3. “Aspen Plus 10. 1”, Manual, Aspen Technology, Inc. , Boston, MA, USA, 2000. 4. “Super Pro Design v. 4. 5”, Manual, INTELLIGEN, INC. , 2001. 3 9


