1 What if…Choice of the functional form

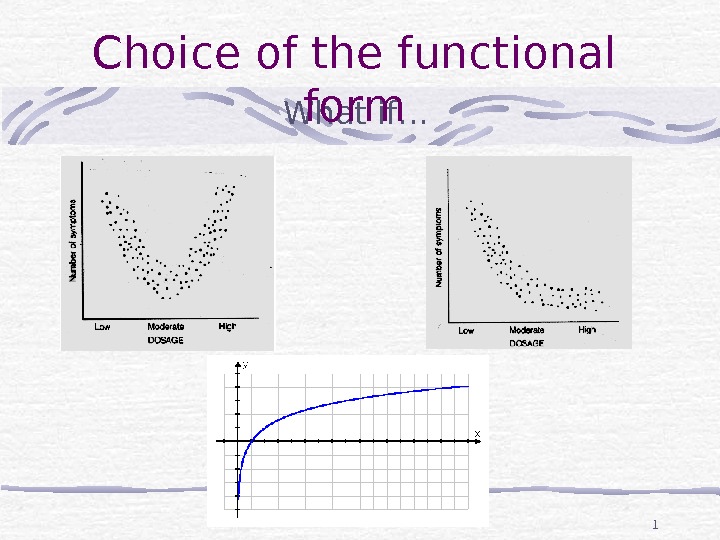
1 What if…Choice of the functional form

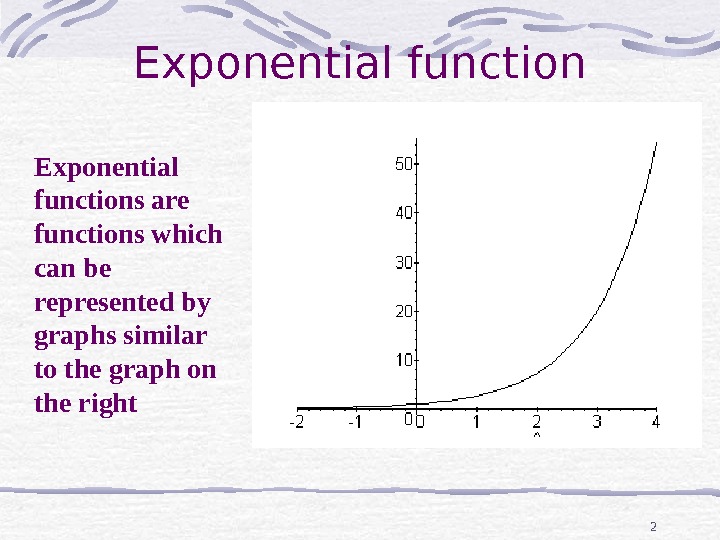
2 Exponential function Exponential f unctions are functions which can be represented by graphs similar to the graph on the right

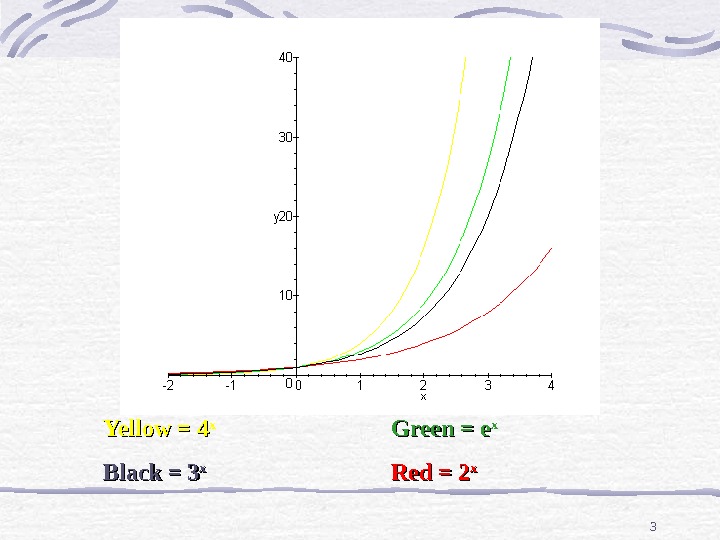
3 Yellow = 4 xx Green = e xx Black = 3 xx Red = 2 xx

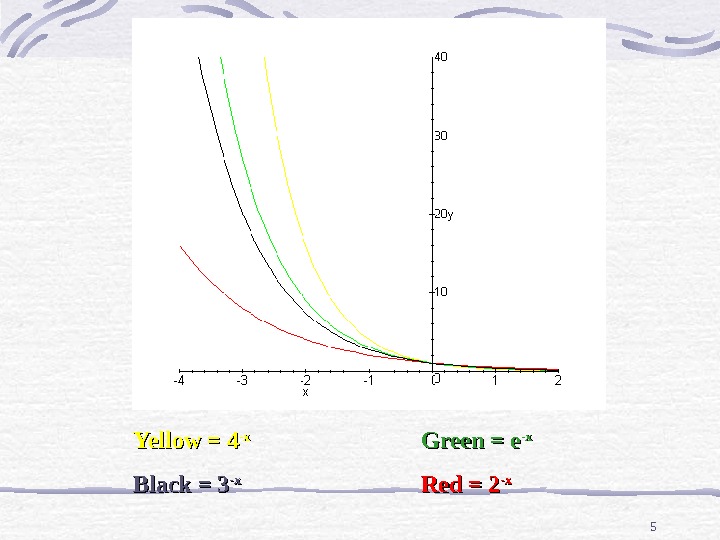
4 As you could see in the graph, the larger the base, the faster the function increased If we place a negative sign in front of the x, the graphs will be reflected(flipped) across the y-axis

5 Yellow = 4 -x-x Green = e -x-x Black = 3 -x-x Red = 2 -x-x

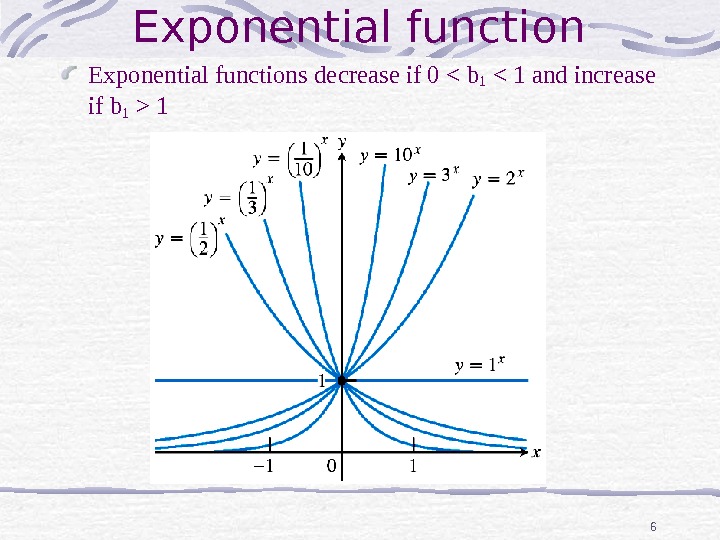
6 Exponential functions decrease if 0 < b 1

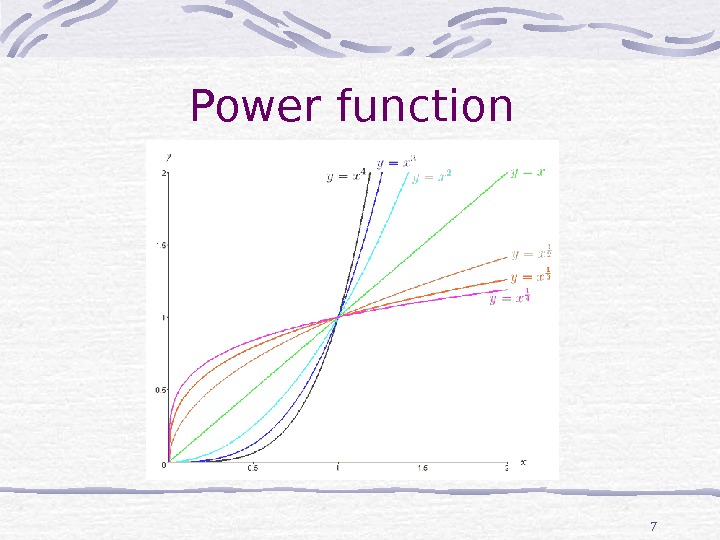
7 Power function

8 Logarithmic function number of methylene groups, n 0 100 200 300 400 500 Tf(exp)/ K

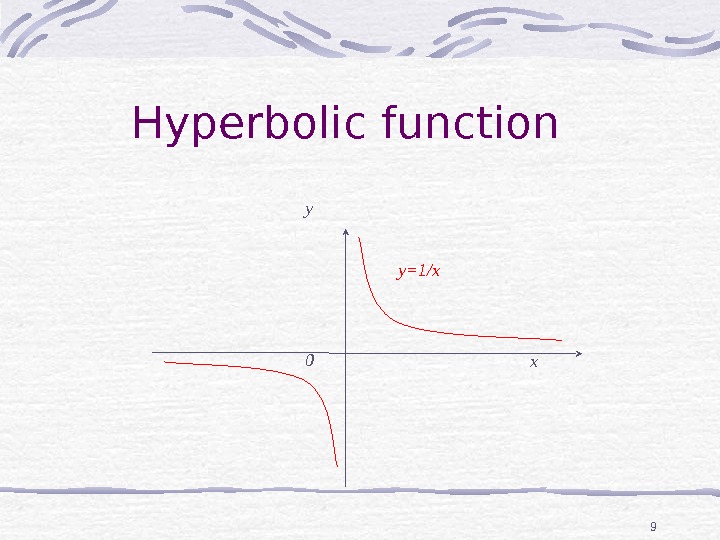
9 Hyperbolic function y x 0 y=1/x

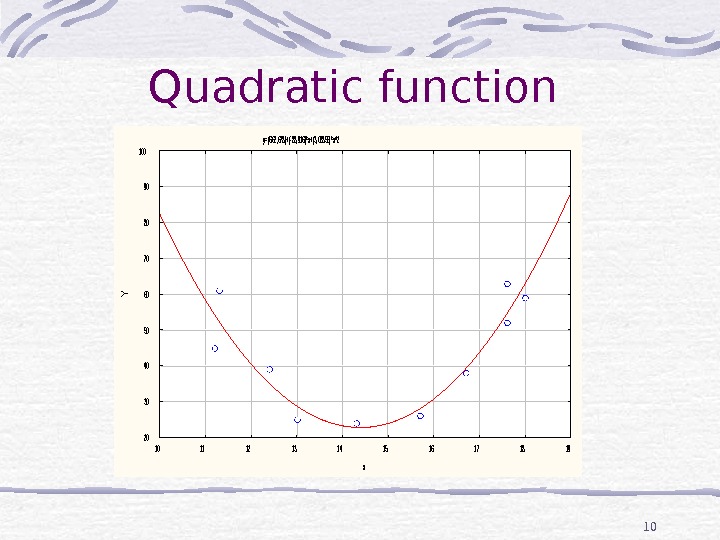
10 Quadratic function y=(662, 678)+(-88, 916)*x+(3, 08855)*x^2 10111213141516171819 x 20 30 40 50 60 70 80 90 100 Y

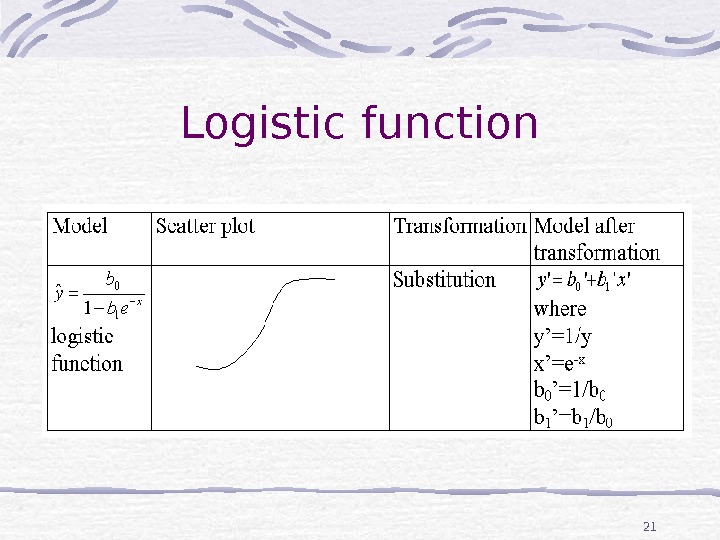
11 Logistic function

12 General information NON LINEAR MODELS OFTEN ARE USED FOR SITUATION IN WHICH THE RATE OF INCREASE OR DECREASE IN THE DEPENDENT VARIABLE (WHEN PLOTTED AGAINST A PARTICULAR INDEPENDENT VARIABLE) IS NOT CONSTANT.

13 General information SOME OF THESE MODELS REQUIRED A TRANSFORMATION TO THE INDEPENDENT VARIABLE.

14 Transformation Logarithms Substitution Data transformations can be used to convert an equation into a linear form

15 Exponential function

16 Power function

17 Quadratic function

18 Polynomial function

19 Hyperbolic function

20 Logarithmic function

21 Logistic function

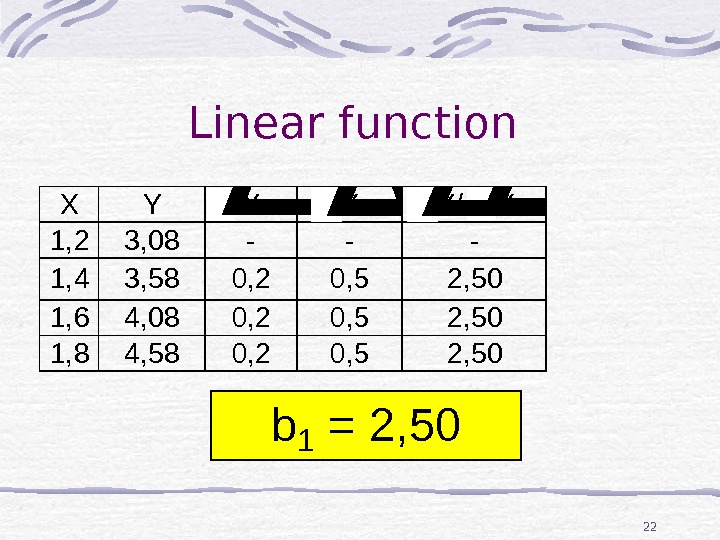
22 Linear function b 1 = 2, 50 X Y 1, 2 3, 08 1, 4 3, 58 1, 6 4, 08 1, 8 4, 58 XY — 0, 20, 5 Y/ X — 2,

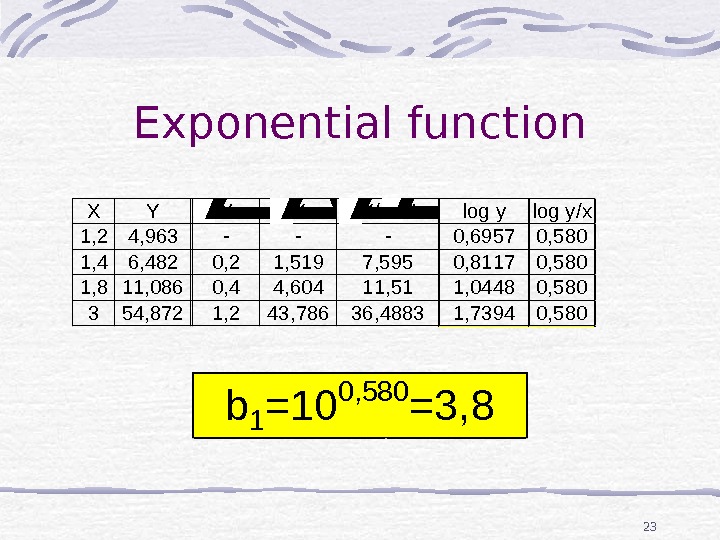
23 Exponential function. XY 1, 24, 963 1, 46, 482 1, 811, 086 354, 872 XY — 0, 21, 519 0, 44, 604 1, 243, 786 Y/ X — 7, 595 11, 51 36, 4883 log y 0, 6957 0, 8117 1, 0448 1, 7394 log y/x 0, 580 b 1 =10 0, 580 =3,

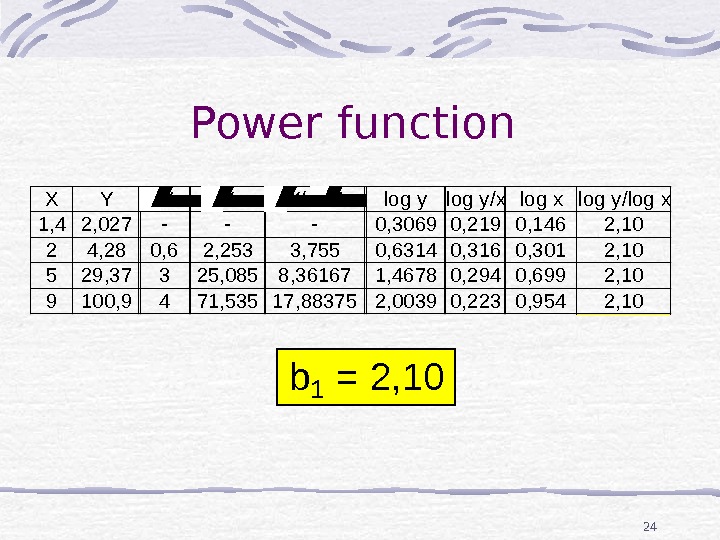
24 Power function XY 1, 42, 027 24, 28 529, 37 9100, 9 XY — 0, 62, 253 325, 085 471, 535 Y/ X — 3, 755 8, 36167 17, 88375 log y 0, 3069 0, 6314 1, 4678 2, 0039 log y/x 0, 219 0, 316 0, 294 0, 223 log x 0, 146 0, 301 0, 699 0, 954 log y/log x 2, 10 b 1 = 2,

25 EXPONENTIAL POWER Independent variable is a power exponent Independent variable is a power base Form of model : x bby 10ˆ1 0ˆ b xby Interpretation of the coefficients b 0 — is the value of Y if independent variable is equal to zero. b 0 — is the value of Y if independent variable is equal to one b 1 — is the growth rate Y. If the independent variable increases 1 unit, the dependent variable will change (increase, if b 1 >1, or decrease, if b 1 0, or decrease, if b 1 <0) b 1 %, on average. Comparison

26 Comparison EXPONENTIAL POWER Linear transformation — logarithms Linear form 10 loglogˆlogbxbyxbbyloglogˆlog 10 Parameters estimation – OLS: YXXX b b. TT log)( log 1 1 0 YXXX b b. TTloglog)log(log 1 1 0 Matrix and vector : 2 xx xn XX T yx y YX T log log 2 )(loglog xx xn XX T yx y YXT loglog

27 Comparison EXPONENTIAL POWER After log b 0 and log b 1 are estimated we should check goodness of fit (standard error of the estimate, indetermination coefficient, test parameters individually and check residuals’ characteristics – at least linearity) for the linear form. 10 loglogˆlogbxbyxbbyloglogˆlog 10 1 )ˆlog(log 2 kn yy S ii e To interpret the results, antilog b 0 and b 1 should be calculated To interpret the results, antilog b 0 should be calculated