

1. Векторный способ y O M 0 x

y M 0 M 1 O x

y M 0 M 1 O x

y M 0 M 1 O x

- закон движения точки -скорость точки в положении М 0 -скорость точки в положении М 1 -Среднее ускорение точки на отрезке пути М 0 М 1

Мгновенное ускорение точки: (1)

2. Координатный способ

(2)

Модуль вектора ускорения: (3) Направление вектора ускорения:

3. Естественный способ М
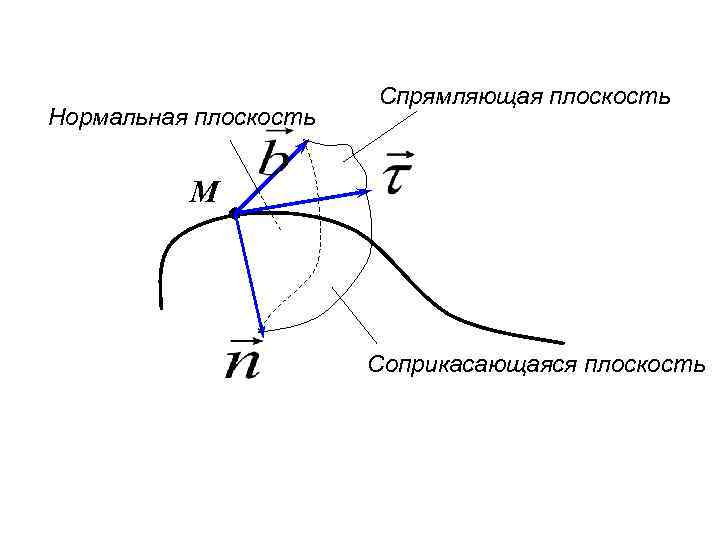
Нормальная плоскость Спрямляющая плоскость М Соприкасающаяся плоскость

М 1 М 2 - дуговая координата - угол смежности

- кривизна кривой -радиус кривизны в данной точке

(4)


(5)

Тангенциальное (касательное) ускорение: (6) Нормальное ускорение: (7) Бинормальное ускорение:

(8)

Сложное движение точки. Теорема Кориолиса Теорема о сложении скоростей: (9)

x x 1 M z 1 O y z y 1 -мгновенная угловая скорость подвижной системы Ox 1 y 1 z 1 относительно неподвижной Ox yz

-приращение радиус-вектора в системе Oxyz -приращение радиус-вектора в системе Ox 1 y 1 z 1 -абсолютная производная -локальная (относительная) производная

(10) (11) (12)

(13) Для вектора ускорения аналогично: (14)

x x 1 M z 1 O z y 1 y - скорость и ускорение точки О 1 в системе. Oxyz

Теорема Кориолиса (15)