1 УСРЕДНЕНИЕ ВЛИЯНИЯ НЕЗАВИСИМЫХ ФАКТОРОВ Закон больших

1 УСРЕДНЕНИЕ ВЛИЯНИЯ НЕЗАВИСИМЫХ ФАКТОРОВ

Закон больших чисел утверждает, что при очень большом числе случайных явлений их средний результат перестает быть случайным и может быть предсказан с большой степенью определенности. Например: • Сумма ежедневных вкладов клиентов в будние дни в среднем является величиной постоянной. • Объем продажи бензина на АЗС в обычные дни является приблизительно постоянным.

Еще один пример: Банк ведет множество финансовых операций: проигрыш по одним операциям компенсируется выигрышем по другим, в следствие чего банк имеет устойчивое финансовое положение. Это утверждение носит название Этот принцип не приносит максимального дохода, но обеспечивает устойчивость положения.

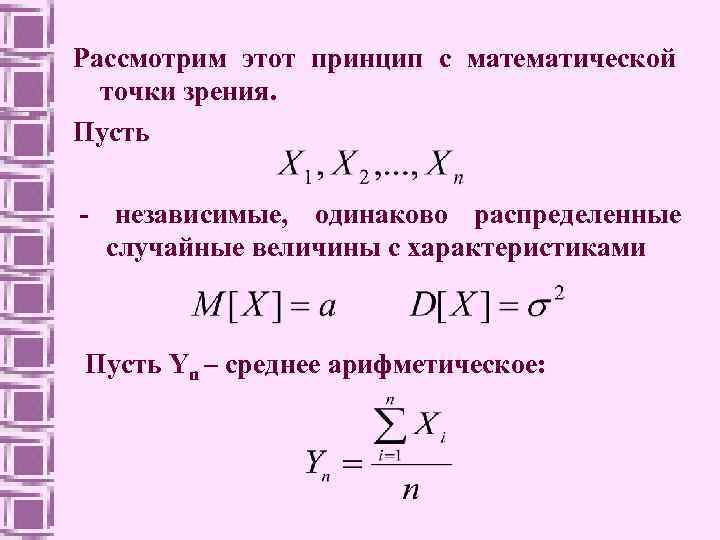
Рассмотрим этот принцип с математической точки зрения. Пусть - независимые, одинаково распределенные случайные величины с характеристиками Пусть Yn – среднее арифметическое:

с характеристиками Если Х трактовать как случайный доход от операций, а среднее квадратичное отклонение – как риск, то При усреднении результатов независимых и приблизительно одинаковых по масштабу операций, средний доход усредняется, а риск уменьшается.

Даны две операции со случайным доходом: -10 0 10 20 0. 1 0. 5 0. 3 -10 0 10 20 0. 1 0. 2 0. 3 0. 4

Найдем средний ожидаемый доход каждой операции, который имеет смысл мат. ожидания. Таким образом, средний ожидаемый доход обеих операций одинаков.

Найдем средний риск каждой который имеет смысл квадратичного отклонения. операции, среднего

Вместо того, чтобы проводить одну операцию, (предположим, что на две операции не хватает средств), вложим денег поровну в каждую: Тогда

Таким образом, при диверсификации средний доход операций остался прежним, а риск уменьшился.

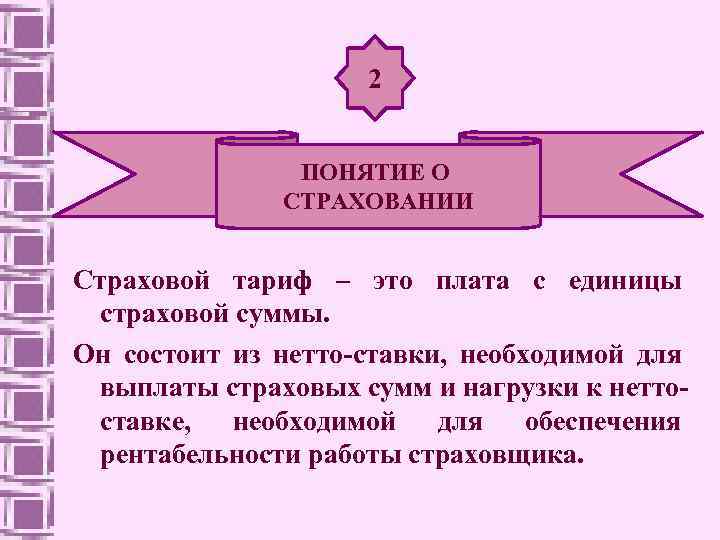
2 ПОНЯТИЕ О СТРАХОВАНИИ Страховой тариф – это плата с единицы страховой суммы. Он состоит из нетто-ставки, необходимой для выплаты страховых сумм и нагрузки к неттоставке, необходимой для обеспечения рентабельности работы страховщика.

Плата со всей страховой суммы называется страховым платежом. Ее платит клиент страховщику. Среднее суммарное страховое возмещение (по всем страховым договорам) должно быть равно страховым платежам по нетто-ставкам. Предположим, что проводится компания по страхованию дачных домиков от пожара сроком на 1 год на сумму S. Какую назначить нетто-ставку и нагрузку к ней?

Пусть n клиентов заключат договор о страховании. Вероятность сгореть для всех домиков одинакова и равна р. Хi – случайная величина, которая принимает два значения: 0 – если домик сгорит; 1 – если домик не сгорит. Все величины Хi одинаково распределены с рядом распределения хi 0 1 pi q p

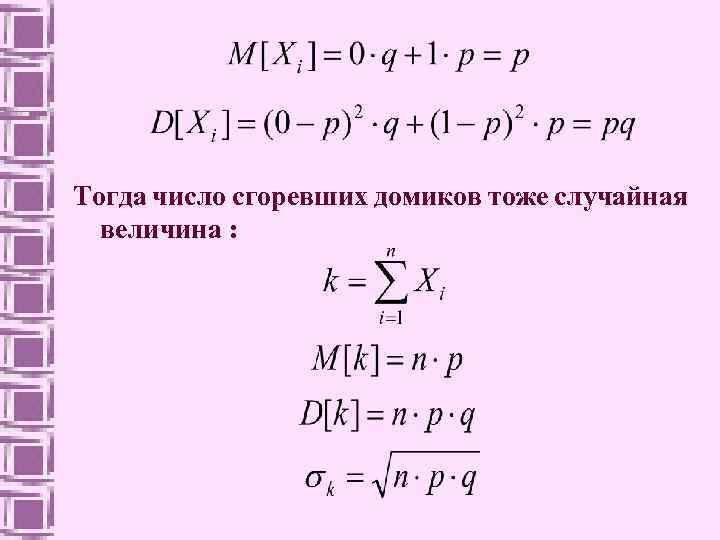
Тогда число сгоревших домиков тоже случайная величина :

Согласно ЦПТ k распределена по нормальному закону. Суммарное страховое возмещение – тоже случайная величина: где S – страховая сумма. Среднее суммарное страховое описывается мат. ожиданием: возмещение

Такую же сумму страховщик должен получить со своих страхователей. Следовательно неттоставка должна быть равна отношению среднего суммарного страхового возмещения к суммарному страховому платежу: Нетто-ставка есть просто вероятность страхового случая.

Теперь найдем нагрузку к нетто-ставке. Т. к. суммарное страховое возмещение W есть случайная величина, то при тарифе, равном нетто-ставке p страховщик получит со всех клиентов сумму По свойству нормального распределения Т. е. в половине случаев страховщик окажется в убытке. Поэтому он должен увеличить тариф.

Пусть γ – вероятность того, что суммарное страховое возмещение W будет меньше суммарного страхового платежа E: Тариф t найдем по теореме Муавра-Лапласа: В нашем случае:

Обозначим за ν функцию Лапласа, при которой

Следовательно, Это и есть основа формирования тарифа. При этом, в среднем суммарные страховые платежи превысят страховое возмещение на величину

2 ОБЕСПЕЧЕНИЕ РЕПРЕЗЕНТАТИВНОСТИ ВЫБОРКИ Выборка из ГС называется репрезентативной, если она позволяет судить о свойствах всей ГС.

Чем больше выборка, тем полнее она отражает свойства ГС, но тем сложнее ее исследовать. Каким образом выбрать оптимальный объем выборки? Предположим, что цель исследования заключается в оценке среднего по ГС или мат. ожидания M[X]. По ЦПТ можно оценить вероятность отклонения среднего арифметического выборки объемом n от мат. ожидания:

Если мы хотим с вероятностью гарантировать, что это отклонение превзойдет по величине ε, то Пусть γ не

В частном случае, когда рассматривается число опытов n, гарантирующее с вероятностью γ, что это отклонение частоты от вероятности не превысит ε, можно поступить так следующим образом. В последней формуле неизвестна Но