41840e95439e5db1fe892b4c2997a1a4.ppt
- Количество слайдов: 133

1 Trilinos Tutorial Overview and Basic Concepts Michael A. Heroux Sandia National Laboratories ACTS Toolkit Workshop 2006 8/22/2006 Sandia is a multiprogram laboratory operated by Sandia Corporation, a Lockheed Martin Company, for the United States Department of Energy under contract DE-AC 04 -94 AL 85000.

Trilinos Development Team Ross Bartlett Lead Developer of Thyra Developer of Rythmos Robert Hoekstra Lead Developer of Epetra. Ext Developer of Epetra, Thyra, Tpetra Eric Phipps Developer of LOCA and NOX Paul Boggs Developer of Thyra Russell Hooper Developer of NOX Marzio Sala Lead Developer of Didasko and IFPACK Developer of ML, Amesos Todd Coffey Lead Developer of Rythmos Vicki Howle Lead Developer of Meros Developer of Belos and Thyra 2 Andrew Salinger Lead Developer of LOCA Jason Cross Developer of Jpetra David Day Developer of Komplex Clark Dohrmann Developer of CLAPS Michael Gee Developer of ML, NOX Bob Heaphy Lead developer of Trilinos SQA Mike Heroux Trilinos Project Leader Lead Developer of Epetra, Aztec. OO, Kokkos, Komplex, IFPACK, Thyra, Tpetra Developer of Amesos, Belos, Epetra. Ext, Jpetra Ulrich Hetmaniuk Developer of Anasazi Jonathan Hu Developer of ML Sarah Knepper Developer of Komplex Tammy Kolda Lead Developer of NOX Joe Kotulski Lead Developer of Pliris Rich Lehoucq Developer of Anasazi and Belos Kevin Long Lead Developer of Thyra, Developer of Belos and Teuchos Roger Pawlowski Lead Developer of NOX Michael Phenow Trilinos Webmaster Lead Developer of New_Package 8/22/2006 Paul Sexton Developer of Epetra and Tpetra Bill Spotz Lead Developer of Py. Trilinos Developer of Epetra, New_Package Ken Stanley Lead Developer of Amesos and New_Package Heidi Thornquist Lead Developer of Anasazi, Belos and Teuchos Ray Tuminaro Lead Developer of ML and Meros Jim Willenbring Developer of Epetra and New_Package. Trilinos library manager Alan Williams Developer of Epetra, Epetra. Ext, Aztec. OO, Tpetra

3 Outline of Talk § § § § 8/22/2006 Background/Motivation. Trilinos Package Concepts. ANAs, LALs and APPs. Managing Parallel Data: Petra Object Model. Whirlwind Tour of Some Trilinos Packages. Generic Programming. SQA/SQE Issues. Concluding remarks.
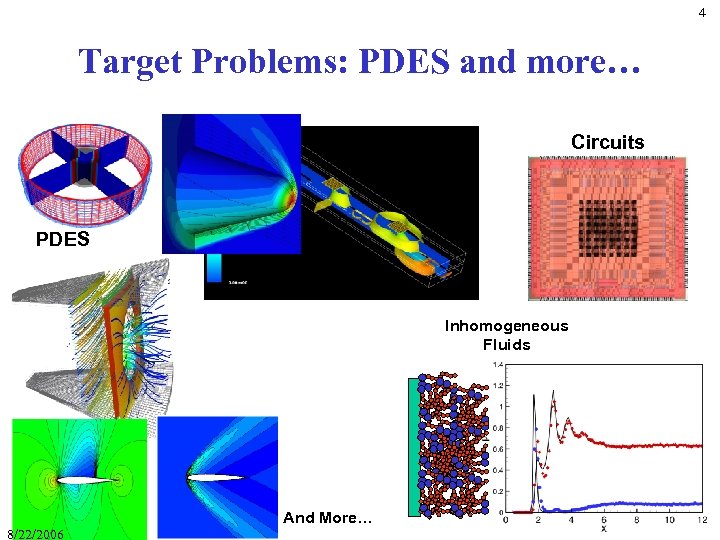
4 Target Problems: PDES and more… Circuits PDES Inhomogeneous Fluids And More… 8/22/2006

5 Motivation For Trilinos § Sandia does LOTS of solver work. § When I started at Sandia in May 1998: w Aztec was a mature package. Used in many codes. w FETI, PETSc, DSCPack, Spooles, ARPACK, DASPK, and many other codes were (and are) in use. w New projects were underway or planned in multi-level preconditioners, eigensolvers, non-linear solvers, etc… § The challenges: w Little or no coordination was in place to: • • Efficiently reuse existing solver technology. Leverage new development across various projects. Support solver software processes. Provide consistent solver APIs for applications. w ASCI was forming software quality assurance/engineering (SQA/SQE) requirements: • Daunting requirements for any single solver effort to address alone. 8/22/2006

6 Evolving Trilinos Solution § Trilinos 1 is an evolving framework to address these challenges: w w Fundamental atomic unit is a package. Includes core set of vector, graph and matrix classes (Epetra/Tpetra packages). Provides a common abstract solver API (Thyra package). Provides a ready-made package infrastructure (new_package): • • Source code management (cvs, bonsai). Build tools (autotools). Automated regression testing (queue directories within repository). Communication tools (mailman mail lists). w Specifies requirements and suggested practices for package SQA. § In general allows us to categorize efforts: w Efforts best done at the Trilinos level (useful to most or all packages). w Efforts best done at a package level (peculiar or important to a package). w Allows package developers to focus only on things that are unique to their package. 1. Trilinos loose translation: “A string of pearls” 8/22/2006
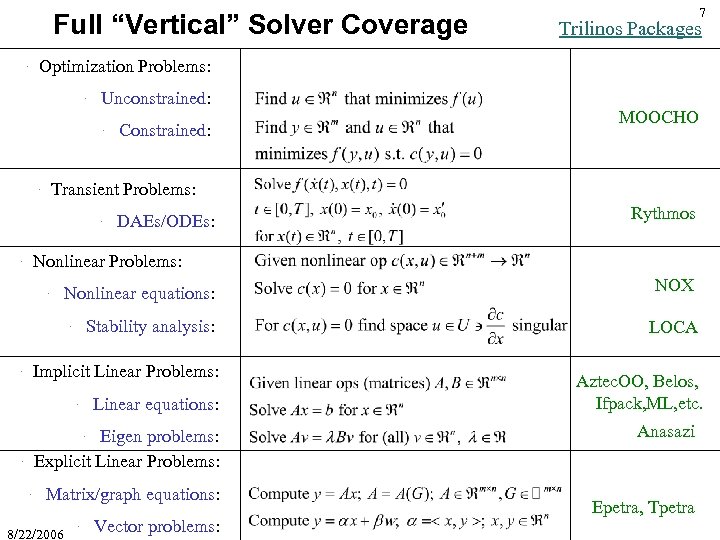
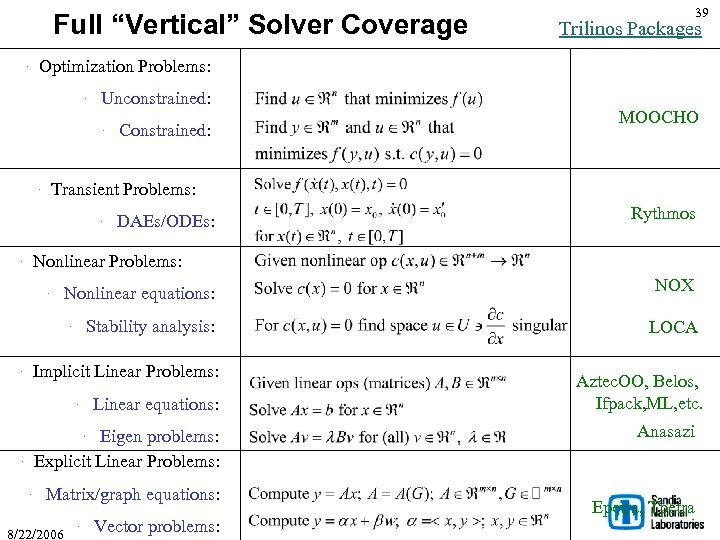
Full “Vertical” Solver Coverage · Unconstrained: · · Constrained: MOOCHO Transient Problems: · DAEs/ODEs: Rythmos Nonlinear Problems: · Nonlinear equations: NOX Stability analysis: LOCA · · Trilinos Packages Optimization Problems: · · 7 Implicit Linear Problems: Linear equations: · Eigen problems: Explicit Linear Problems: · · · Matrix/graph equations: 8/22/2006 · Vector problems: Aztec. OO, Belos, Ifpack, ML, etc. Anasazi Epetra, Tpetra
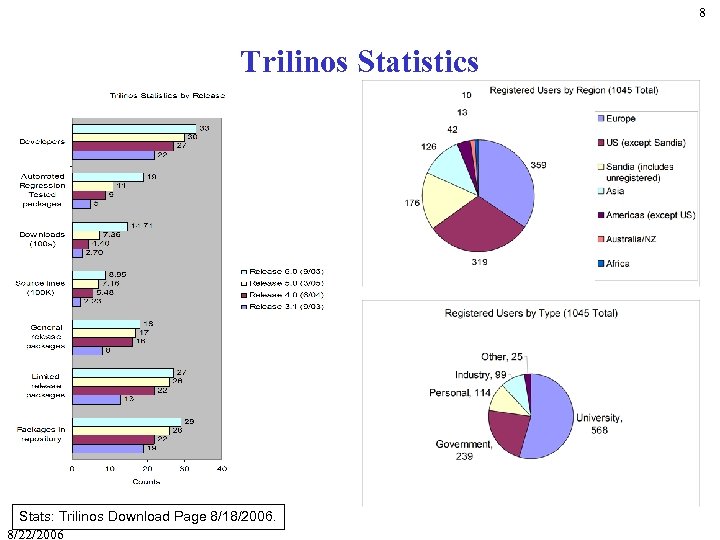
8 Trilinos Statistics Stats: Trilinos Download Page 8/18/2006. 8/22/2006

9 Trilinos Package Concepts Package: The Atomic Unit 8/22/2006

10 Trilinos Packages § Trilinos is a collection of Packages. § Each package is: w Focused on important, state-of-the-art algorithms in its problem regime. w Developed by a small team of domain experts. w Self-contained: No explicit dependencies on any other software packages (with some special exceptions). w Configurable/buildable/documented on its own. § Sample packages: NOX, Aztec. OO, ML, IFPACK, Meros. § Special package collections: w w 8/22/2006 Petra (Epetra, Tpetra, Jpetra): Concrete Data Objects Thyra: Abstract Conceptual Interfaces Teuchos: Common Tools. New_package: Jumpstart prototype.

11 Greek Names 8/22/2006
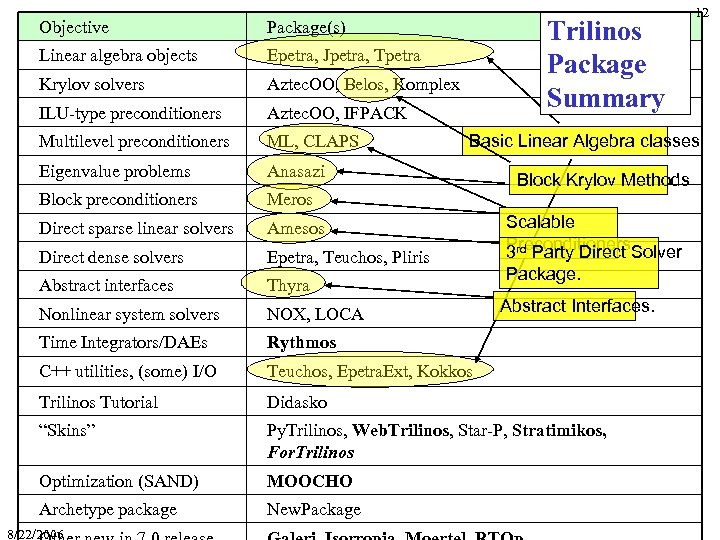
Trilinos Package Summary Objective Package(s) Linear algebra objects Epetra, Jpetra, Tpetra Krylov solvers Aztec. OO, Belos, Komplex ILU-type preconditioners Aztec. OO, IFPACK Multilevel preconditioners ML, CLAPS Eigenvalue problems Anasazi Block preconditioners Meros Direct sparse linear solvers Amesos Direct dense solvers Epetra, Teuchos, Pliris Abstract interfaces Thyra Nonlinear system solvers NOX, LOCA Time Integrators/DAEs Rythmos C++ utilities, (some) I/O Teuchos, Epetra. Ext, Kokkos Trilinos Tutorial Didasko “Skins” Py. Trilinos, Web. Trilinos, Star-P, Stratimikos, For. Trilinos Optimization (SAND) MOOCHO Archetype package New. Package 8/22/2006 12 Basic Linear Algebra classes Block Krylov Methods Scalable Preconditioners 3 rd Party Direct Solver Package. Abstract Interfaces.

13 Why Packages? Let’s Do Some Matrix Analysis! 8/22/2006

Trilinos Development Team (Again) Ross Bartlett Lead Developer of Thyra Developer of Rythmos Robert Hoekstra Lead Developer of Epetra. Ext Developer of Epetra, Thyra, Tpetra Eric Phipps Developer of LOCA and NOX Paul Boggs Developer of Thyra Russell Hooper Developer of NOX Marzio Sala Lead Developer of Didasko and IFPACK Developer of ML, Amesos Todd Coffey Lead Developer of Rythmos Vicki Howle Lead Developer of Meros Developer of Belos and Thyra 14 Andrew Salinger Lead Developer of LOCA Jason Cross Developer of Jpetra David Day Developer of Komplex Clark Dohrmann Developer of CLAPS Michael Gee Developer of ML, NOX Bob Heaphy Lead developer of Trilinos SQA Mike Heroux Trilinos Project Leader Lead Developer of Epetra, Aztec. OO, Kokkos, Komplex, IFPACK, Thyra, Tpetra Developer of Amesos, Belos, Epetra. Ext, Jpetra Ulrich Hetmaniuk Developer of Anasazi Jonathan Hu Developer of ML Sarah Knepper Developer of Komplex Tammy Kolda Lead Developer of NOX Joe Kotulski Lead Developer of Pliris Rich Lehoucq Developer of Anasazi and Belos Kevin Long Lead Developer of Thyra, Developer of Belos and Teuchos Roger Pawlowski Lead Developer of NOX Michael Phenow Trilinos Webmaster Lead Developer of New_Package 8/22/2006 Paul Sexton Developer of Epetra and Tpetra Bill Spotz Lead Developer of Py. Trilinos Developer of Epetra, New_Package Ken Stanley Lead Developer of Amesos and New_Package Heidi Thornquist Lead Developer of Anasazi, Belos and Teuchos Ray Tuminaro Lead Developer of ML and Meros Jim Willenbring Developer of Epetra and New_Package. Trilinos library manager Alan Williams Developer of Epetra, Epetra. Ext, Aztec. OO, Tpetra

15 Developer and Package Node IDs Developer IDs Package IDs Ross. Bartlett = 1; Paul. Boggs = 2; Todd. Coffey = 3; Jason. Cross = 4; David. Day = 5; Clark. Dohrmann= 6; Michael. Gee = 7; Bob. Heaphy = 8; Mike. Heroux = 9; Ulrich. Hetmaniuk = 10; Rob. Hoekstra = 11; Russell. Hooper = 12; Vicki. Howle = 13; Jonathan. Hu = 14; Sarah. Knepper = 15; Tammy. Kolda = 16; Joe. Kotulski = 17; Rich. Lehoucq = 18; Kevin. Long = 19; Roger. Pawlowski = 20; Michael. Phenow = 21; Eric. Phipps = 22; Marzio. Sala = 23; Andrew. Salinger = 24; Paul. Sexton = 25; Bill. Spotz = 26; Ken. Stanley = 27; Heidi. Thornquist = 28; Ray. Tuminaro = 29; Jim. Willenbring = 30; Alan. Williams = 31; Py. Trilinos = 1; amesos = 2; anasazi = 3; aztecoo = 4; belos = 5; claps = 6; didasko = 7; epetra = 8; epetraext = 9; ifpack = 10; jpetra = 11; kokkos = 12; komplex = 13; meros = 14; loca = 15; ml = 16; new_package = 17; nox = 18; pliris = 19; rythmos = 20; teuchos = 21; thyra = 22; tpetra = 23; trilinosframework = 24; 8/22/2006

16 Developer-Package Edges A(i, j) = 1 if developer i contributes to package j A = sparse(31, 24); A(Ross. Bartlett, rythmos) = 1; A(Ross. Bartlett, thyra) = 1; A(Paul. Boggs, thyra) = 1; A(Todd. Coffey, rythmos) = 1; A(Jason. Cross, jpetra) = 1; A(David. Day, komplex) = 1; A(Clark. Dohrmann, claps) = 1; A(Michael. Gee, ml) = 1; A(Michael. Gee, nox) = 1; A(Bob. Heaphy, trilinosframework) = 1; A(Mike. Heroux, epetra) = 1; A(Mike. Heroux, aztecoo) = 1; A(Mike. Heroux, kokkos) = 1; A(Mike. Heroux, komplex) = 1; A(Mike. Heroux, ifpack) = 1; A(Mike. Heroux, thyra) = 1; A(Mike. Heroux, tpetra) = 1; A(Mike. Heroux, amesos) = 1; A(Mike. Heroux, belos) = 1; A(Mike. Heroux, epetraext) = 1; A(Mike. Heroux, jpetra) = 1; A(Ulrich. Hetmaniuk, anasazi) = 1; 8/22/2006 A(Rob. Hoekstra, epetra) = 1; A(Rob. Hoekstra, thyra) = 1; A(Rob. Hoekstra, tpetra) = 1; A(Rob. Hoekstra, epetraext) = 1; A(Russell. Hooper, nox) = 1; A(Vicki. Howle, meros) = 1; A(Vicki. Howle, belos) = 1; A(Vicki. Howle, thyra) = 1; A(Jonathan. Hu, ml) = 1; A(Sarah. Knepper, komplex) = 1; A(Tammy. Kolda, nox) = 1; A(Tammy. Kolda, trilinosframework) = 1; A(Joe. Kotulski, pliris) = 1; A(Rich. Lehoucq, anasazi) = 1; A(Rich. Lehoucq, belos) = 1; A(Kevin. Long, thyra) = 1; A(Kevin. Long, belos) = 1; A(Kevin. Long, teuchos) = 1; A(Roger. Pawlowski, nox) = 1; A(Michael. Phenow, trilinosframework) = 1; A(Eric. Phipps, loca) = 1; A(Eric. Phipps, nox) = 1; A(Marzio. Sala, didasko) = 1; A(Marzio. Sala, ifpack) = 1; A(Marzio. Sala, ml) = 1; A(Marzio. Sala, amesos) = 1; A(Andrew. Salinger, loca) = 1; A(Paul. Sexton, epetra) = 1; A(Paul. Sexton, tpetra) = 1; A(Bill. Spotz, Py. Trilinos) = 1; A(Bill. Spotz, epetra) = 1; A(Bill. Spotz, new_package) = 1; A(Ken. Stanley, amesos) = 1; A(Ken. Stanley, new_package) = 1; A(Heidi. Thornquist, anasazi) = 1; A(Heidi. Thornquist, belos) = 1; A(Heidi. Thornquist, teuchos) = 1; A(Ray. Tuminaro, ml) = 1; A(Ray. Tuminaro, meros) = 1; A(Jim. Willenbring, epetra) = 1; A(Jim. Willenbring, new_package) = 1; A(Jim. Willenbring, trilinosframework) = 1; A(Alan. Williams, epetraext) = 1; A(Alan. Williams, aztecoo) = 1; A(Alan. Williams, tpetra) = 1;
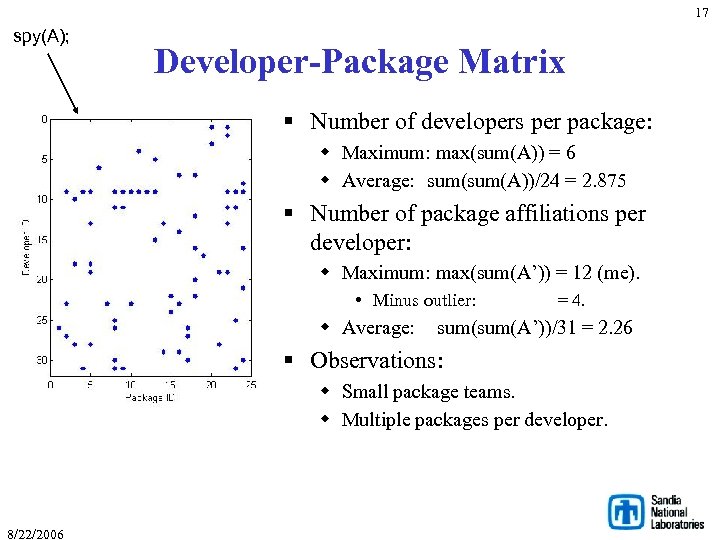
17 spy(A); Developer-Package Matrix § Number of developers per package: w Maximum: max(sum(A)) = 6 w Average: sum(A))/24 = 2. 875 § Number of package affiliations per developer: w Maximum: max(sum(A’)) = 12 (me). • Minus outlier: = 4. w Average: sum(A’))/31 = 2. 26 § Observations: w Small package teams. w Multiple packages per developer. 8/22/2006
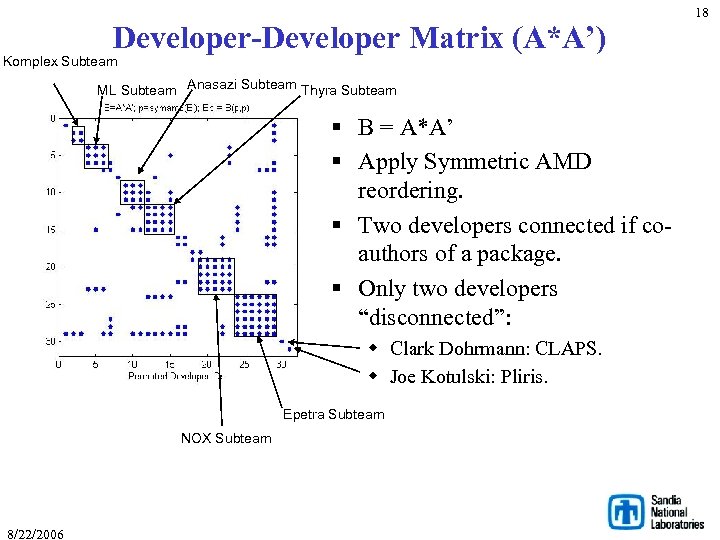
Developer-Developer Matrix (A*A’) Komplex Subteam ML Subteam Anasazi Subteam Thyra Subteam § B = A*A’ § Apply Symmetric AMD reordering. § Two developers connected if coauthors of a package. § Only two developers “disconnected”: w Clark Dohrmann: CLAPS. w Joe Kotulski: Pliris. Epetra Subteam NOX Subteam 8/22/2006 18

19 Package-Package Matrix (A’*A) (Not sure what to say about this) § B = A’*A, Apply symamd. w Two packages connected if they share a developer. w Only two packages “disconnected”: • Clark Dohrmann: CLAPS. • Joe Kotulski: Pliris. Without Me Me Meros, Aztec. OO, Tpetra, Epetra. Ext Epetra, Amesos, Didasko, Ifpack 8/22/2006

20 Why Packages? Partial Answer: Small Inter-related teams. 8/22/2006

21 Package Interoperability 8/22/2006

22 Interoperability vs. Dependence (“Can Use”) (“Depends On”) § Although most Trilinos packages have no explicit dependence, each package must interact with some other packages: w NOX needs operator, vector and solver objects. w Aztec. OO needs preconditioner, matrix, operator and vector objects. w Interoperability is enabled at configure time. For example, NOX: --enable-nox-lapack compile NOX lapack interface libraries --enable-nox-epetra compile NOX epetra interface libraries --enable-nox-petsc compile NOX petsc interface libraries § Trilinos configure script is vehicle for: . . /configure –enable-pytho w Establishing interoperability of Trilinos components… w Without compromising individual package autonomy. § Trilinos offers seven basic interoperability mechanisms. 8/22/2006

Trilinos Interoperability Mechanisms (Acquired as Package Matures) Package builds under Trilinos configure scripts. Package accepts user data as Epetra or Thyra objects Applications using Epetra/Thyra can use package Package accepts parameters from Teuchos Parameter. Lists Applications using Teuchos Parameter. Lists can drive package Package can be used via Thyra abstract solver classes Applications or other packages using Thyra can use package Package can use Epetra for private data. Package can then use other packages that understand Epetra Package accesses solver services via Thyra interfaces Package can then use other packages that implement Thyra interfaces Package available via Py. Trilinos 8/22/2006 Package can be built as part of a suite of packages; cross-package interfaces enable/disable automatically Package can be used with other Trilinos packages via Python. 23
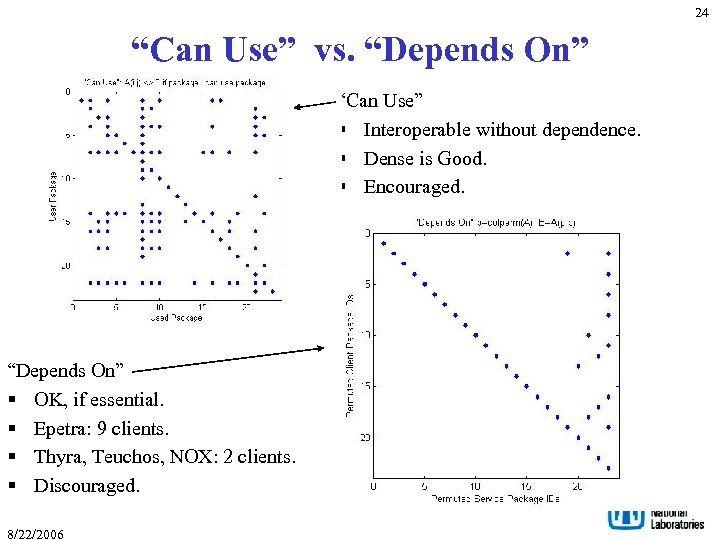
24 “Can Use” vs. “Depends On” “Can Use” § Interoperable without dependence. § Dense is Good. § Encouraged. “Depends On” § OK, if essential. § Epetra: 9 clients. § Thyra, Teuchos, NOX: 2 clients. § Discouraged. 8/22/2006

25 Interoperability Example: ML § ML: Multi-level Preconditioner Package. § Primary Developers: Ray Tuminaro, Jonathan Hu, Marzio Sala. § No explicit, essential dependence on other Trilinos packages. w Uses abstract interfaces to matrix/operator objects. w Has independent configure/build process (but can be invoked at Trilinos level). § Interoperable with other Trilinos packages and other libraries: w w w w 8/22/2006 Accepts user data as Epetra matrices/vectors. Can use Epetra for internal matrices/vectors. Can be used via Thyra abstract interfaces. Can be built via Trilinos configure/build process. Available as preconditioner to all other Trilinos packages. Can use IFPACK, Amesos, Aztec. OO objects as smoothers, coarse solvers. Can be driven via Teuchos Parameter. Lists. Available to PETSc users without dependence on any other Trilinos packages.

26 Package Maturation Process Asynchronicity 8/22/2006

27 Day 1 of Package Life § § CVS: Each package is self-contained in Trilinos/package/ directory. Bugzilla: Each package has its own Bugzilla product. Bonsai: Each package is browsable via Bonsai interface. Mailman: Each Trilinos package, including Trilinos itself, has four mail lists: w package-checkins@software. sandia. gov • CVS commit emails. “Finger on the pulse” list. w package-developers@software. sandia. gov • Mailing list for developers. w package-users@software. sandia. gov • Issues for package users. w package-announce@software. sandia. gov • Releases and other announcements specific to the package. § New_package (optional): Customizable boilerplate for w Autoconf/Automake/Doxygen/Python/Thyra/Epetra/Test. Harness/Website 8/22/2006

Sample Package Maturation Process Step Package added to CVS: Import existing code or start with new_package. Example ML CVS repository migrated into Trilinos (July 2002). Mail lists, Bugzilla Product, Bonsai database created. ml-announce, ml-users, ml-developers, ml-checkins, mlregression @software. sandia. gov created, linked to CVS (July 2002). Package builds with configure/make, Trilinoscompatible ML adopts Autoconf, Automake starting from new_package (June 2003). Epetra objects recognized by package. ML accepts user data as Epetra matrices and vectors (October 2002). Package accessible via Thyra interfaces. ML adaptors written for TSFCore_Lin. Op (Thyra) interface (May 2003). Package uses Epetra for internal data. ML able to generate Epetra matrices. Allows use of Aztec. OO, Amesos, Ifpack, etc. as smoothers and coarse grid solvers (Feb. June 2004). Package parameters settable via Teuchos Parameter. List ML gets manager class, driven via Parameter. Lists (June 2004). Package usable from Python (Py. Trilinos) ML Python wrappers written using new_package template (April 2005). 8/22/2006 Startup Steps Maturation Steps 28

29 Maturation Jumpstart: New. Package § New. Package provides jump start to develop/integrate a new package § New. Package is a “Hello World” program and website: w Simple but it does work with autotools. w Compiles and builds. § New. Package directory contains: w w w Commonly used directory structure: src, test, doc, example, config. Working Autoconf/Automake files. Documentation templates (doxygen). Working regression test setup. Working Python and Thyra adaptors. § Substantially cuts down on: w Time to integrate new package. w Variation in package integration details. w Development of website. NOTE: New. Package can be used independent from Trilinos 8/22/2006

30 What Trilinos is not § Trilinos is not a single monolithic piece of software. Each package: w w Can be built independent of Trilinos. Has its own self-contained CVS structure. Has its own Bugzilla product and mail lists. Development team is free to make its own decisions about algorithms, coding style, release contents, testing process, etc. § Trilinos top layer is not a large amount of source code: w Trilinos repository (6. 0 branch) contains: 660, 378 source lines of code (SLOC). w Sum of the packages SLOC counts : 648, 993. w Trilinos top layer SLOC count: 11, 385 (1. 7%). § Trilinos is not “indivisible”: w You don’t need all of Trilinos to get things done. w Any collection of packages can be combined and distributed. w Current public release contains only 16 of the 20+ Trilinos packages. 8/22/2006

31 Insight from History A Philosophy for Future Directions § In the early 1800’s U. S. had many new territories. § Question: How to incorporate into U. S. ? w w Colonies? No. Expand boundaries of existing states? No. Create process for self-governing regions. Yes. Theme: Local control drawing on national resources. § Trilinos package architecture has some similarities: w Asynchronous maturation. w Packages decide degree of interoperations, use of Trilinos facilities. § Strength of each: Scalable growth with local control. 8/22/2006

32 Solver Collaboration: The Big Picture 8/22/2006
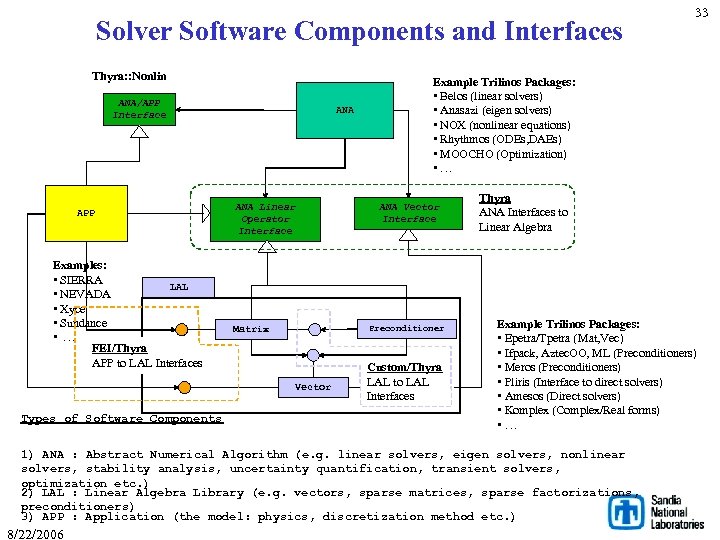
Solver Software Components and Interfaces Thyra: : Nonlin ANA/APP Interface APP Examples: • SIERRA LAL • NEVADA • Xyce • Sundance • … FEI/Thyra APP to LAL Interfaces ANA Linear Operator Interface Vector Types of Software Components Example Trilinos Packages: • Belos (linear solvers) • Anasazi (eigen solvers) • NOX (nonlinear equations) • Rhythmos (ODEs, DAEs) • MOOCHO (Optimization) • … ANA Vector Interface Preconditioner Matrix Custom/Thyra LAL to LAL Interfaces Thyra ANA Interfaces to Linear Algebra Example Trilinos Packages: • Epetra/Tpetra (Mat, Vec) • Ifpack, Aztec. OO, ML (Preconditioners) • Meros (Preconditioners) • Pliris (Interface to direct solvers) • Amesos (Direct solvers) • Komplex (Complex/Real forms) • … 1) ANA : Abstract Numerical Algorithm (e. g. linear solvers, eigen solvers, nonlinear solvers, stability analysis, uncertainty quantification, transient solvers, optimization etc. ) 2) LAL : Linear Algebra Library (e. g. vectors, sparse matrices, sparse factorizations, preconditioners) 3) APP : Application (the model: physics, discretization method etc. ) 8/22/2006 33

34 LAL Foundation: Petra § Petra provides a “common language” for distributed linear algebra objects (operator, matrix, vector) § Petra provides distributed matrix and vector services. § Has 3 implementations under development. 8/22/2006
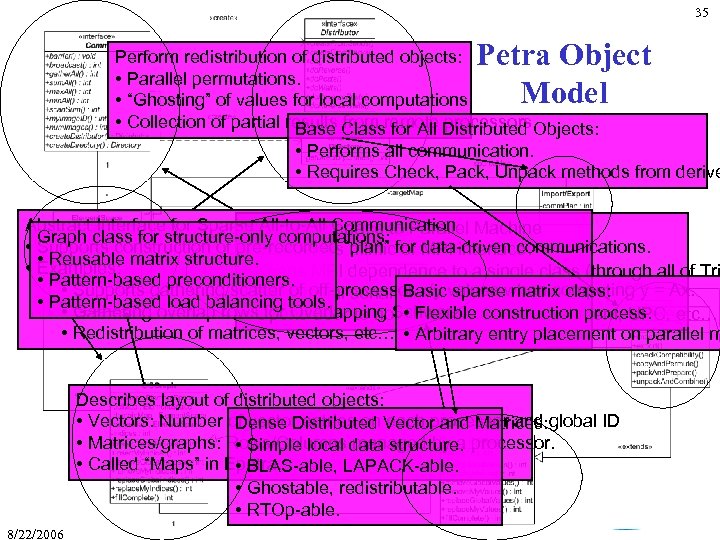
35 Petra Object Model Perform redistribution of distributed objects: • Parallel permutations. • “Ghosting” of values for local computations. • Collection of partial results from remote processors. Base Class for All Distributed Objects: • Performs all communication. • Requires Check, Pack, Unpack methods from derive Abstract Interface for Sparse All-to-All Communication Abstract Interface to Parallel Machine Graph class for structure-only computations: • Supports construction of pre-recorded “plan” for data-driven communications. • Shameless mimic of MPI interface. • Reusable matrix structure. • Examples: • Keeps MPI dependence to a single class (through all of Tri • Pattern-based preconditioners. • Supports gathering/scatter of off-processor x/y values when computing y = Ax. Basic sparse matrix class: • Allow trivial serial implementation. • Pattern-based load balancing tools. • Gathering overlap rows for Overlapping Schwarz. • Flexible construction process. • Opens door to novel parallel libraries (shmem, UPC, etc…) • Redistribution of matrices, vectors, etc… • Arbitrary entry placement on parallel m Describes layout of distributed objects: • Vectors: Number of vector entries on each processor and global ID Dense Distributed Vector and Matrices: • Matrices/graphs: Rows/Columns managed by a processor. • Simple local data structure. • Called “Maps” in Epetra. • BLAS-able, LAPACK-able. • Ghostable, redistributable. • RTOp-able. 8/22/2006

36 Petra Implementations § Three version under development: § Epetra (Essential Petra): w w Current production version. Restricted to real, double precision arithmetic. Uses stable core subset of C++ (circa 2000). Interfaces accessible to C and Fortran users. § Tpetra (Templated Petra): w Next generation C++ version. w Templated scalar and ordinal fields. w Uses namespaces, and STL: Improved usability/efficiency. § Jpetra (Java Petra): w Pure Java. Portable to any JVM. w Interfaces to Java versions of MPI, LAPACK and BLAS via interfaces. 8/22/2006

37 Data Model Wrap-Up § Our target apps require flexible data model. § Petra Object Model (POM) supports: w Arbitrary placement of vector, graph, matrix entries on parallel machine. w Arbitrary redistribution, ghosting and collection of distributed data. § This flexibility is needed by LALs: w Algebraic and multi-level preconditioners. w Concrete distributed matrix kernels. w Direct methods. § POM is complex: Non-LALs (ANAs) do not rely on it. 8/22/2006

38 Abstract Numerical Algorithms (ANAs) 8/22/2006
Full “Vertical” Solver Coverage · Unconstrained: · · Constrained: MOOCHO Transient Problems: · DAEs/ODEs: Rythmos Nonlinear Problems: · Nonlinear equations: NOX Stability analysis: LOCA · · Trilinos Packages Optimization Problems: · · 39 Implicit Linear Problems: Linear equations: · Eigen problems: Explicit Linear Problems: · · · Matrix/graph equations: 8/22/2006 · Vector problems: Aztec. OO, Belos, Ifpack, ML, etc. Anasazi Epetra, Tpetra

40 Goal of Abstraction: Flexibility § Linear solvers (Direct, Iterative, Preconditioners) w Abstraction of basic vector/matrix operations (dot, axpy, mv). w Can use any concrete linear algebra library (Epetra, PETSc, BLAS). § Nonlinear solvers (Newton, etc. ) w + Abstraction of linear solve (solve Ax=b). w Can use any concrete linear solver library (Aztec. OO, ML, PETSc, LAPACK). § Transient/DAE solvers (implicit) w + Abstraction of nonlinear solve. w … and so on. § But how do we really make it work, and retain high performance? § Our answer: Thyra. 8/22/2006
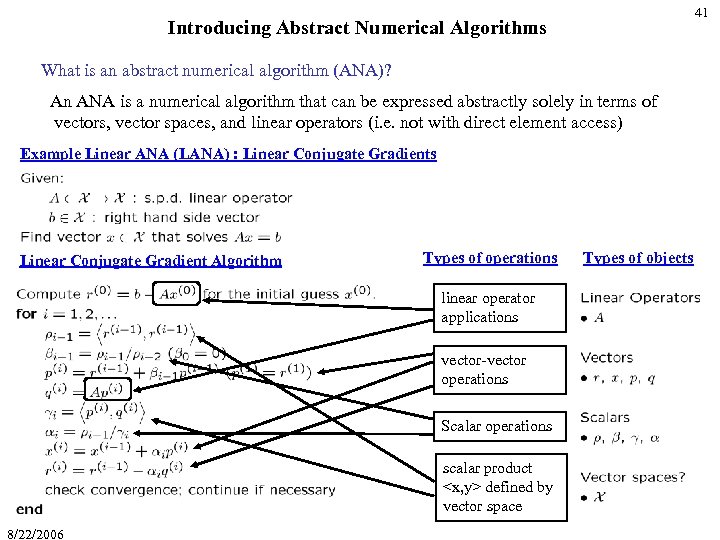
41 Introducing Abstract Numerical Algorithms What is an abstract numerical algorithm (ANA)? An ANA is a numerical algorithm that can be expressed abstractly solely in terms of vectors, vector spaces, and linear operators (i. e. not with direct element access) Example Linear ANA (LANA) : Linear Conjugate Gradients Linear Conjugate Gradient Algorithm Types of operations linear operator applications vector-vector operations Scalar operations scalar product <x, y> defined by vector space 8/22/2006 Types of objects
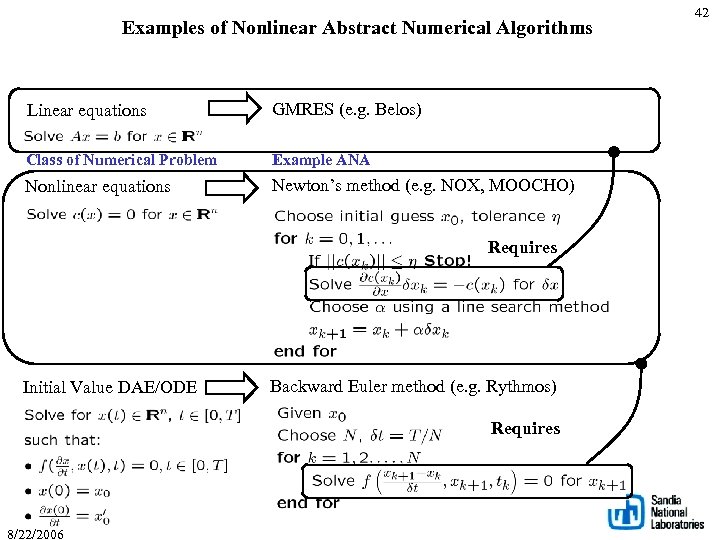
Examples of Nonlinear Abstract Numerical Algorithms Linear equations GMRES (e. g. Belos) Class of Numerical Problem Example ANA Nonlinear equations Newton’s method (e. g. NOX, MOOCHO) Requires Initial Value DAE/ODE Backward Euler method (e. g. Rythmos) Requires 8/22/2006 42
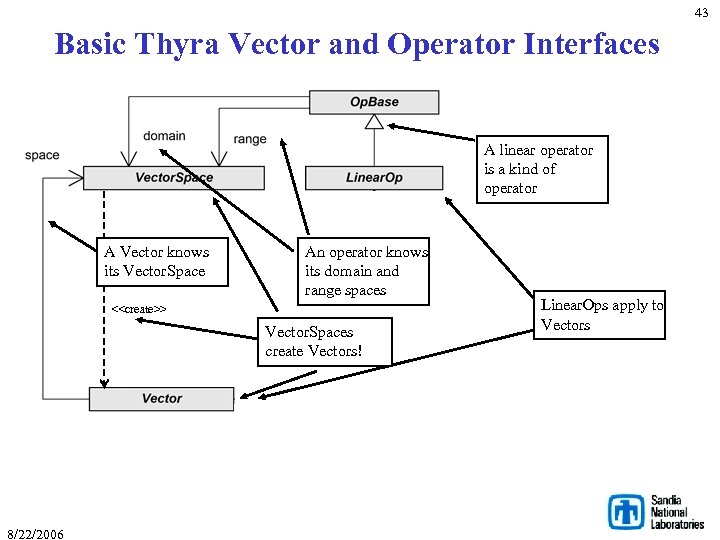
43 Basic Thyra Vector and Operator Interfaces A linear operator is a kind of operator A Vector knows its Vector. Space An operator knows its domain and range spaces <<create>> Vector. Spaces create Vectors! 8/22/2006 Linear. Ops apply to Vectors
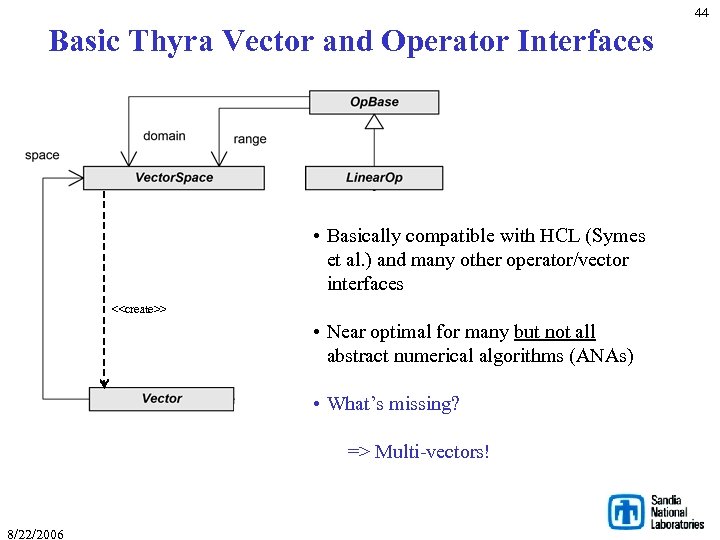
44 Basic Thyra Vector and Operator Interfaces • Basically compatible with HCL (Symes et al. ) and many other operator/vector interfaces <<create>> • Near optimal for many but not all abstract numerical algorithms (ANAs) • What’s missing? => Multi-vectors! 8/22/2006
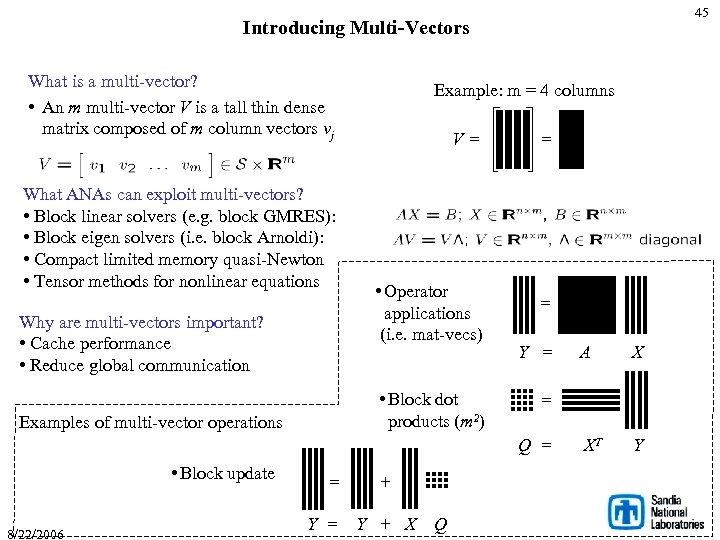
45 Introducing Multi-Vectors What is a multi-vector? • An m multi-vector V is a tall thin dense matrix composed of m column vectors vj What ANAs can exploit multi-vectors? • Block linear solvers (e. g. block GMRES): • Block eigen solvers (i. e. block Arnoldi): • Compact limited memory quasi-Newton • Tensor methods for nonlinear equations Why are multi-vectors important? • Cache performance • Reduce global communication Example: m = 4 columns V= • Operator applications (i. e. mat-vecs) • Block dot products (m 2) Examples of multi-vector operations = = Y = 8/22/2006 = Y = + Y + X Q X XT Y = Q = • Block update A
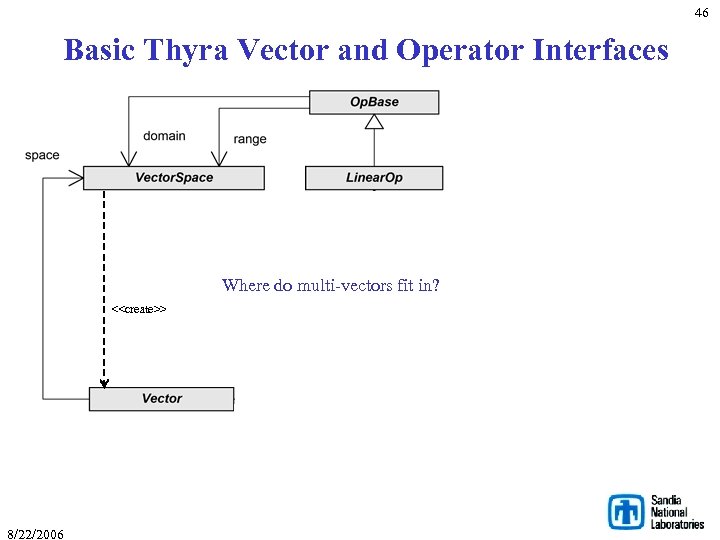
46 Basic Thyra Vector and Operator Interfaces Where do multi-vectors fit in? <<create>> 8/22/2006
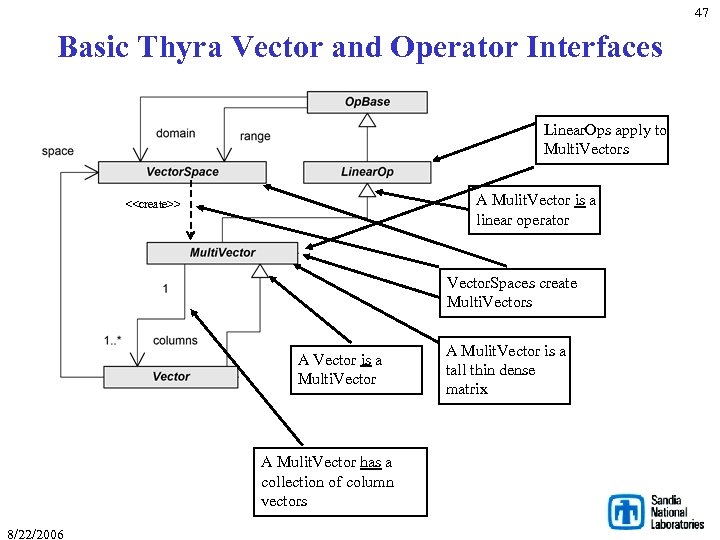
47 Basic Thyra Vector and Operator Interfaces Linear. Ops apply to Multi. Vectors A Mulit. Vector is a linear operator <<create>> Vector. Spaces create Multi. Vectors A Vector is a Multi. Vector A Mulit. Vector has a collection of column vectors 8/22/2006 A Mulit. Vector is a tall thin dense matrix
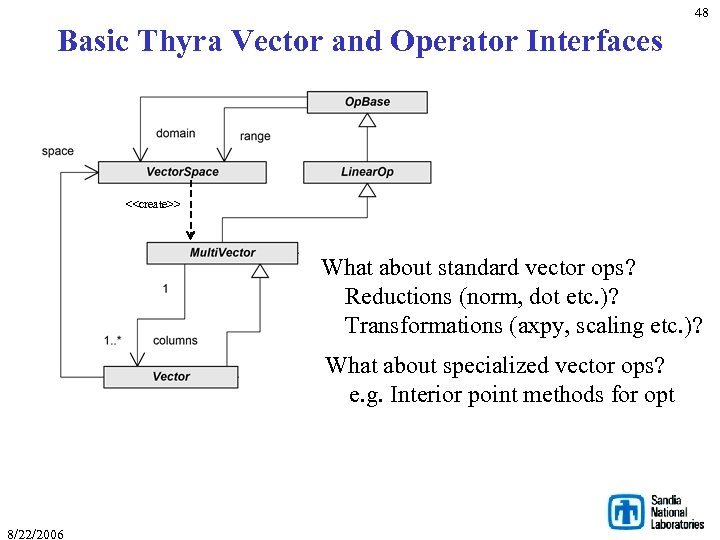
48 Basic Thyra Vector and Operator Interfaces <<create>> What about standard vector ops? Reductions (norm, dot etc. )? Transformations (axpy, scaling etc. )? What about specialized vector ops? e. g. Interior point methods for opt 8/22/2006

What’s the Big Deal about Vector-Vector Operations? Examples from OOQP (Gertz, Wright) Example from TRICE (Dennis, Heinkenschloss, Vicente) Example from IPOPT (Waechter) Many different and unusual vector operations are needed by interior point methods for optimization! Currently in MOOCHO : > 40 vector operations! 8/22/2006 49
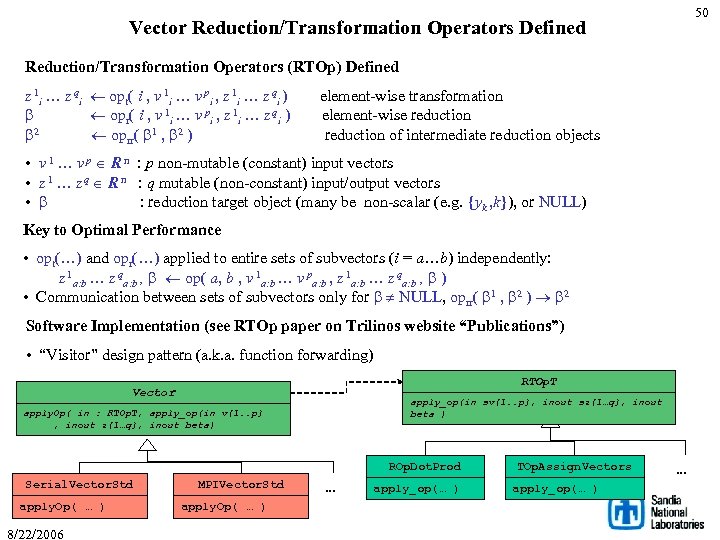
50 Vector Reduction/Transformation Operators Defined Reduction/Transformation Operators (RTOp) Defined z 1 i … z qi ¬ opt( i , v 1 i … v pi , z 1 i … z qi ) element-wise transformation b ¬ opr( i , v 1 i … v pi , z 1 i … z qi ) element-wise reduction b 2 ¬ oprr( b 1 , b 2 ) reduction of intermediate reduction objects • v 1 … v p Î R n : p non-mutable (constant) input vectors • z 1 … z q Î R n : q mutable (non-constant) input/output vectors • b : reduction target object (many be non-scalar (e. g. {yk , k}), or NULL) Key to Optimal Performance • opt(…) and opr(…) applied to entire sets of subvectors (i = a…b) independently: z 1 a: b … z qa: b , b ¬ op( a, b , v 1 a: b … v pa: b , z 1 a: b … z qa: b , b ) • Communication between sets of subvectors only for b ¹ NULL, oprr( b 1 , b 2 ) ® b 2 Software Implementation (see RTOp paper on Trilinos website “Publications”) • “Visitor” design pattern (a. k. a. function forwarding) RTOp. T Vector apply_op(in sv[1. . p], inout sz[1…q], inout beta ) apply. Op( in : RTOp. T, apply_op(in v[1. . p] , inout z[1…q], inout beta) ROp. Dot. Prod Serial. Vector. Std apply. Op( … ) 8/22/2006 MPIVector. Std apply. Op( … ) … apply_op(… ) TOp. Assign. Vectors apply_op(… ) …
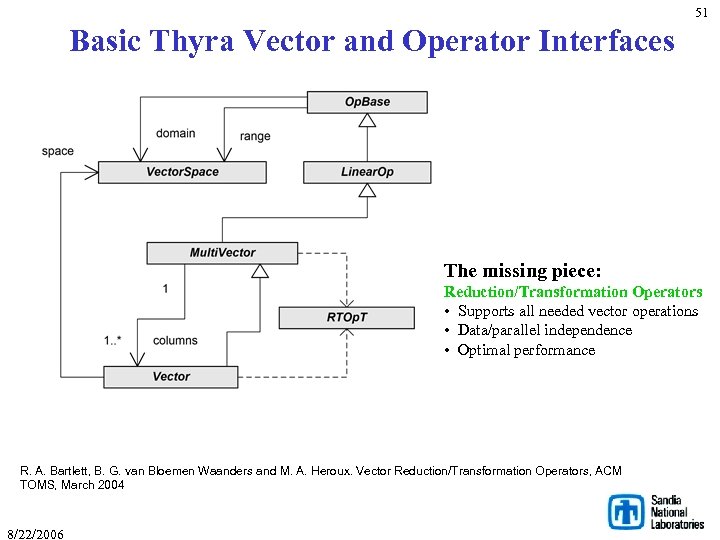
51 Basic Thyra Vector and Operator Interfaces The missing piece: Reduction/Transformation Operators • Supports all needed vector operations • Data/parallel independence • Optimal performance R. A. Bartlett, B. G. van Bloemen Waanders and M. A. Heroux. Vector Reduction/Transformation Operators, ACM TOMS, March 2004 8/22/2006

52 Managing Parallel Data The Petra Object Model 8/22/2006

53 A Simple Epetra/Aztec. OO Program // Header files omitted… int main(int argc, char *argv[]) { MPI_Init(&argc, &argv); // Initialize MPI, Mpi. Comm Epetra_Mpi. Comm( MPI_COMM_WORLD ); // ***** Create x and b vectors ***** Epetra_Vector x(Map); Epetra_Vector b(Map); b. Random(); // Fill RHS with random #s // ***** Map puts same number of equations on each pe ***** int Num. My. Elements = 1000 ; Epetra_Map Map(-1, Num. My. Elements, 0, Comm); int Num. Global. Elements = Map. Num. Global. Elements(); // ***** Create an Epetra_Matrix tridiag(-1, 2, -1) ***** Epetra_Crs. Matrix A(Copy, Map, 3); double neg. One = -1. 0; double pos. Two = 2. 0; for (int i=0; i<Num. My. Elements; i++) { int Global. Row = A. GRID(i); int Row. Less 1 = Global. Row - 1; int Row. Plus 1 = Global. Row + 1; if (Row. Less 1!=-1) A. Insert. Global. Values(Global. Row, 1, &neg. One, &Row. Less 1); if (Row. Plus 1!=Num. Global. Elements) A. Insert. Global. Values(Global. Row, 1, &neg. One, &Row. Plus 1); A. Insert. Global. Values(Global. Row, 1, &pos. Two, &Global. Row); } A. Fill. Complete(); // Transform from GIDs to LIDs 8/22/2006 // ***** Create Linear Problem ***** Epetra_Linear. Problem problem(&A, &x, &b); // ***** Create/define Aztec. OO instance, solve ***** Aztec. OO solver(problem); solver. Set. Aztec. Option(AZ_precond, AZ_Jacobi); solver. Iterate(1000, 1. 0 E-8); // ***** Report results, finish ************ cout << "Solver performed " << solver. Num. Iters() << " iterations. " << endl << "Norm of true residual = " << solver. True. Residual() << endl; MPI_Finalize() ; return 0; }
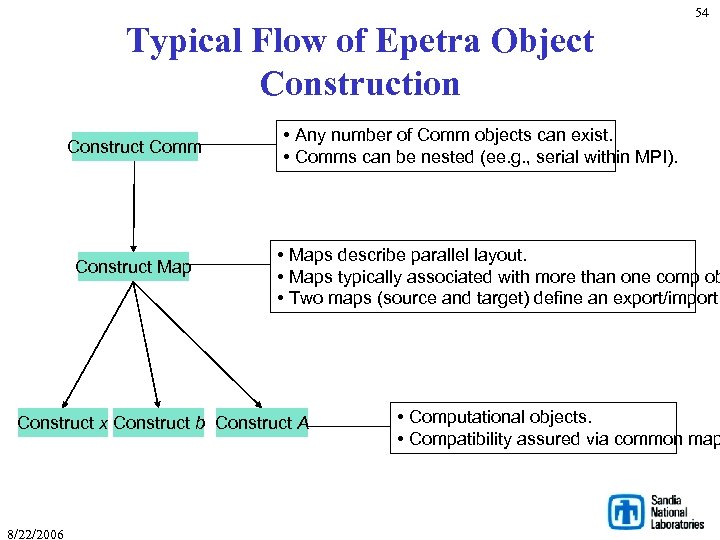
Typical Flow of Epetra Object Construction Construct Comm Construct Map • Any number of Comm objects can exist. • Comms can be nested (ee. g. , serial within MPI). • Maps describe parallel layout. • Maps typically associated with more than one comp ob • Two maps (source and target) define an export/import Construct x Construct b Construct A 8/22/2006 54 • Computational objects. • Compatibility assured via common map

55 Parallel Data Redistribution § § Epetra vectors, multivectors, graphs and matrices are distributed via one of the map objects. A map is basically a partitioning of a list of global IDs: w IDs are simply labels, no need to use contiguous values (Directory class handles details for general ID lists). w No a priori restriction on replicated IDs. § If we are given: w A source map and w A set of vectors, multivectors, graphs and matrices (or other distributable objects) based on source map. § Redistribution is performed by: 1. Specifying a target map with a new distribution of the global IDs. 2. Creating Import or Export object using the source and target maps. 3. Creating vectors, multivectors, graphs and matrices that are redistributed (to target map layout) using the Import/Export object. 8/22/2006
![Example: epetra/ex 9. cpp int main(int argc, char *argv[]) { MPI_Init(&argc, &argv); Epetra_Mpi. Comm(MPI_COMM_WORLD); Example: epetra/ex 9. cpp int main(int argc, char *argv[]) { MPI_Init(&argc, &argv); Epetra_Mpi. Comm(MPI_COMM_WORLD);](https://present5.com/presentation/41840e95439e5db1fe892b4c2997a1a4/image-56.jpg)
Example: epetra/ex 9. cpp int main(int argc, char *argv[]) { MPI_Init(&argc, &argv); Epetra_Mpi. Comm(MPI_COMM_WORLD); int Num. Global. Elements = 4; // global dimension of the problem int Num. My. Elements; // local nodes Epetra_Int. Serial. Dense. Vector My. Global. Elements; if( Comm. My. PID() == 0 ) { Num. My. Elements = 3; My. Global. Elements. Size(Num. My. Elements); My. Global. Elements[0] = 0; My. Global. Elements[1] = 1; My. Global. Elements[2] = 2; } else { Num. My. Elements = 3; My. Global. Elements. Size(Num. My. Elements); My. Global. Elements[0] = 1; My. Global. Elements[1] = 2; My. Global. Elements[2] = 3; } // create a map Epetra_Map Map(-1, My. Global. Elements. Length(), My. Global. Elements. Values(), 0, Comm); 8/22/2006 56 // create a vector based on map Epetra_Vector xxx(Map); for( int i=0 ; i<Num. My. Elements ; ++i ) xxx[i] = 10*( Comm. My. PID()+1 ); if( Comm. My. PID() == 0 ){ double val = 12; int pos = 3; xxx. Sum. Into. Global. Values(1, 0, &val, &pos); } cout << xxx; // create a target map, in which all elements are on proc 0 int Num. My. Elements_target; if( Comm. My. PID() == 0 ) Num. My. Elements_target = Num. Global. Elements; else Num. My. Elements_target = 0; Epetra_Map Target. Map(-1, Num. My. Elements_target, 0, Comm); Epetra_Exporter(Map, Target. Map); // work on vectors Epetra_Vector yyy(Target. Map); yyy. Export(xxx, Exporter, Add); cout << yyy; MPI_Finalize(); return( EXIT_SUCCESS ); }
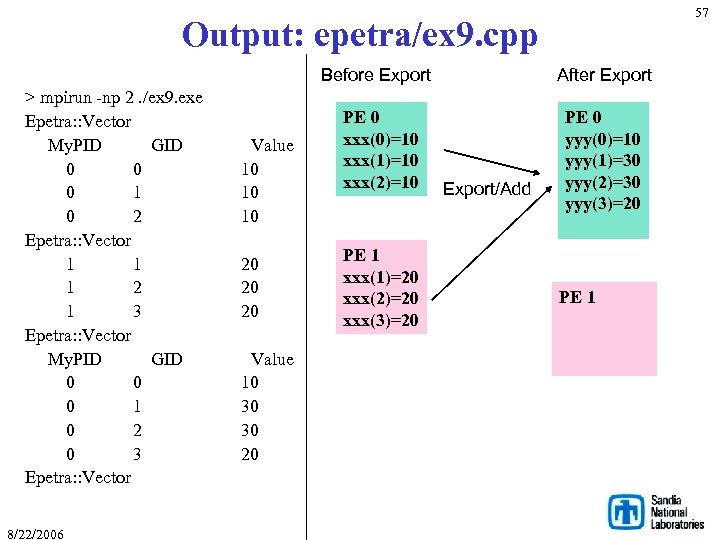
57 Output: epetra/ex 9. cpp Before Export > mpirun -np 2. /ex 9. exe Epetra: : Vector My. PID GID Value 0 10 1 10 2 10 Epetra: : Vector 1 20 1 2 20 1 3 20 Epetra: : Vector My. PID GID Value 0 10 1 30 2 30 3 20 Epetra: : Vector 8/22/2006 After Export PE 0 xxx(0)=10 xxx(1)=10 xxx(2)=10 PE 0 yyy(0)=10 yyy(1)=30 yyy(2)=30 yyy(3)=20 PE 1 xxx(1)=20 xxx(2)=20 xxx(3)=20 Export/Add PE 1

58 Import vs. Export § Import (Export) means calling processor knows what it wants to receive (send). § Distinction between Import/Export is important to user, almost identical in implementation. § Import (Export) objects can be used to do an Export (Import) as a reverse operation. § When mapping is bijective (1 -to-1 and onto), either Import or Export is appropriate. 8/22/2006

59 Example: 1 D Matrix Assembly -uxx = f u(a) = 0 u(b) = 1 PE 0 a x 1 PE 1 x 2 x 3 b • 3 Equations: Find u at x 1, x 2 and x 3 • Equation for u at x 2 gets a contribution from PE 0 and PE 1. • Would like to compute partial contributions independently. • Then combine partial results. 8/22/2006

60 Two Maps § We need two maps: w Assembly map: • PE 0: { 1, 2 }. • PE 1: { 2, 3 }. w Solver map: • PE 0: { 1, 2 } (we arbitrate ownership of 2). • PE 1: { 3 }. 8/22/2006
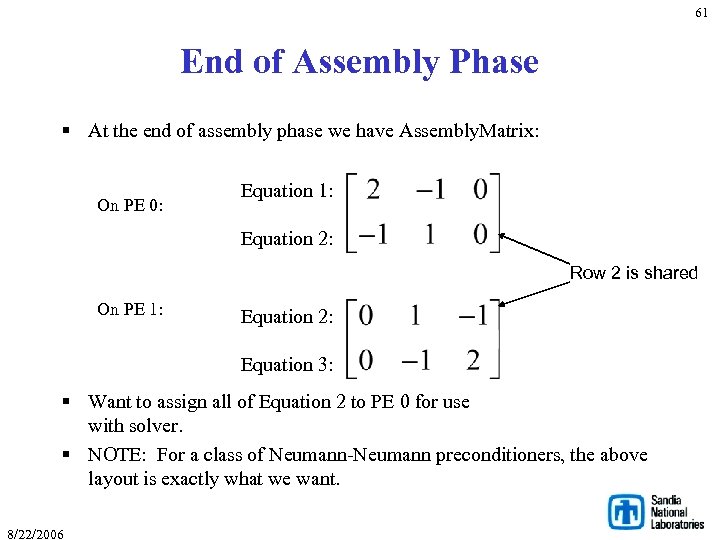
61 End of Assembly Phase § At the end of assembly phase we have Assembly. Matrix: On PE 0: Equation 1: Equation 2: Row 2 is shared On PE 1: Equation 2: Equation 3: § Want to assign all of Equation 2 to PE 0 for use with solver. § NOTE: For a class of Neumann-Neumann preconditioners, the above layout is exactly what we want. 8/22/2006

Export Assembly Matrix to Solver Matrix Epetra_Exporter(Assembly. Map, Solver. Map); Epetra_Crs. Matrix Solver. Matrix (Copy, Solver. Map, 0); Solver. Matrix. Export(Assembly. Matrix, Exporter, Add); Solver. Matrix. Fill. Complete(); 8/22/2006 62
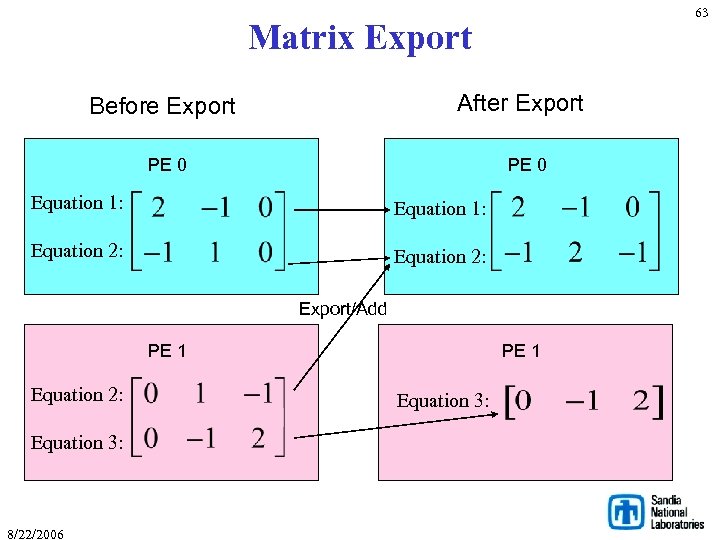
63 Matrix Export After Export Before Export PE 0 Equation 1: Equation 2: Export/Add PE 1 Equation 2: Equation 3: 8/22/2006 PE 1 Equation 3:
![Example: epetraext/ex 2. cpp int main(int argc, char *argv[]) { MPI_Init(&argc, &argv); Epetra_Mpi. Comm Example: epetraext/ex 2. cpp int main(int argc, char *argv[]) { MPI_Init(&argc, &argv); Epetra_Mpi. Comm](https://present5.com/presentation/41840e95439e5db1fe892b4c2997a1a4/image-64.jpg)
Example: epetraext/ex 2. cpp int main(int argc, char *argv[]) { MPI_Init(&argc, &argv); Epetra_Mpi. Comm (MPI_COMM_WORLD); int My. PID = Comm. My. PID(); int n=4; // Generate Laplacian 2 d gallery matrix Trilinos_Util: : Crs. Matrix. Gallery G("laplace_2 d", Comm); G. Set("problem_size", n*n); G. Set("map_type", "linear"); // Linear map initially // Get the Linear. Problem. Epetra_Linear. Problem *Prob = G. Get. Linear. Problem(); // Get the exact solution. Epetra_Multi. Vector *sol = G. Get. Exact. Solution(); // Get the rhs (b) and lhs (x) Epetra_Multi. Vector *b = Prob->Get. RHS(); Epetra_Multi. Vector *x = Prob->Get. LHS(); 8/22/2006 64 // Repartition graph using Zoltan Epetra. Ext: : Zoltan_Crs. Graph * Zoltan. Trans = new Epetra. Ext: : Zoltan_Crs. Graph(); Epetra. Ext: : Linear. Problem_Graph. Trans * Zoltan. LPTrans = new Epetra. Ext: : Linear. Problem_Graph. Trans( *(dynamic_cast<Epetra. Ext: : Structural. Same. Type. Transfo rm<Epetra_Crs. Graph>*>(Zoltan. Trans)) ); cout << "Creating Load Balanced Linear Problemn"; Epetra_Linear. Problem &Balanced. Prob = (*Zoltan. LPTrans)(*Prob); // Get the rhs (b) and lhs (x) Epetra_Multi. Vector *Balancedb = Prob->Get. RHS(); Epetra_Multi. Vector *Balancedx = Prob->Get. LHS(); cout << "Balanced b: " << *Balancedb << endl; cout << "Balanced x: " << *Balancedx << endl; MPI_Finalize() ; return 0 ; }

65 Need for Import/Export § Solvers for complex engineering applications need expressive, easy-to-use parallel data redistribution: w Allows better scaling for non-uniform overlapping Schwarz. w Necessary for robust solution of multiphysics problems. § We have found import and export facilities to be a very natural and powerful technique to address these issues. 8/22/2006

66 Details about Epetra Maps § Getting beyond standard use case… 8/22/2006

67 1 -to-1 Maps § 1 -to-1 map (defn): A map is 1 -to-1 if each GID appears only once in the map (and is therefore associated with only a single processor). § Certain operations in parallel data repartitioning require 1 to-1 maps. Specifically: w w 8/22/2006 The source map of an import must be 1 -to-1. The target map of an export must be 1 -to-1. The domain map of a 2 D object must be 1 -to-1. The range map of a 2 D object must be 1 -to-1.

68 2 D Objects: Four Maps § Epetra 2 D objects: w Crs. Matrix w Crs. Graph w Vbr. Matrix § Have four maps: Typically a 1 -to-1 map Typically NOT a 1 -to-1 map w Row. Map: On each processor, the GIDs of the rows that processor will “manage”. w Col. Map: On each processor, the GIDs of the columns that processor will “manage”. w Domain. Map: The layout of domain objects (the x vector/multivector in y=Ax). Must be 1 -to-1 maps!!! w Range. Map: The layout of range objects (the y vector/multivector in y=Ax). 8/22/2006
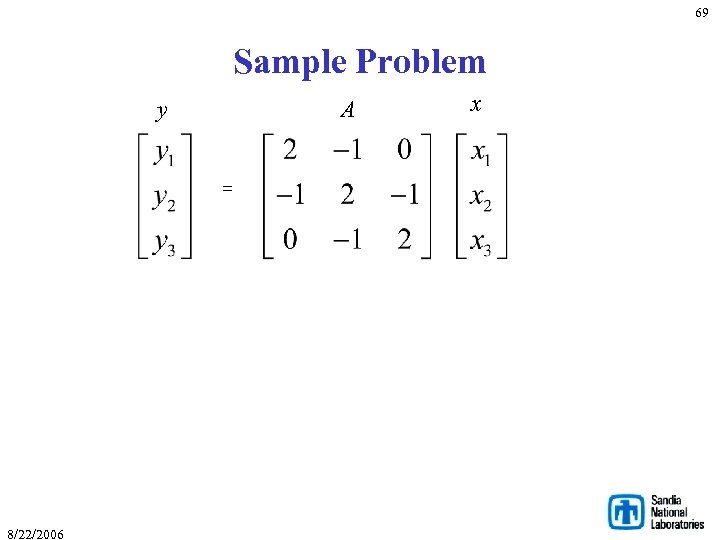
69 Sample Problem y A = 8/22/2006 x

Case 1: Standard Approach 70 w First 2 rows of A, elements of y and elements of x, kept on PE 0. w Last row of A, element of y and element of x, kept on PE 1. PE 0 Contents § § Row. Map Col. Map Domain. Map Range. Map PE 1 Contents A = 8/22/2006 Row. Map Col. Map Domain. Map Range. Map = {2} = {1, 2} = {2} Notes: Original Problem y § § = {0, 1} = {0, 1, 2} = {0, 1} x § § Rows are wholly owned. Row. Map=Domain. Map=Range. Map (all 1 -to-1). Col. Map is NOT 1 -to-1. Call to Fill. Complete: A. Fill. Complete(); // Assumes

71 Case 2: Twist 1 w First 2 rows of A, first element of y and last 2 elements of x, kept on PE 0. w Last row of A, last 2 element of y and first element of x, kept on PE 1. PE 0 Contents § § Row. Map Col. Map Domain. Map Range. Map PE 1 Contents A = 8/22/2006 Row. Map Col. Map Domain. Map Range. Map = {2} = {1, 2} = {0} = {1, 2} Notes: Original Problem y § § = {0, 1} = {0, 1, 2} = {0} x § § Rows are wholly owned. Row. Map is NOT = Domain. Map is NOT = Range. Map (all 1 -to-1). Col. Map is NOT 1 -to-1. Call to Fill. Complete: A. Fill. Complete(Domain. Map, Range. Map);

Case 2: Twist 2 72 w First row of A, part of second row of A, first element of y and last 2 elements of x, kept on PE 0. w Last row, part of second row of A, last 2 element of y and first element of x, kept on PE 1. PE 0 Contents PE 1 Contents § § Row. Map Col. Map Domain. Map Range. Map § § = {0, 1} = {1, 2} = {0} A = 8/22/2006 = {1, 2} = {0} = {1, 2} Notes: Original Problem y Row. Map Col. Map Domain. Map Range. Map x § § Rows are NOT wholly owned. Row. Map is NOT = Domain. Map is NOT = Range. Map (all 1 -to-1). Row. Map and Col. Map are NOT 1 -to-1. Call to Fill. Complete: A. Fill. Complete(Domain. Map, Range. Map);

73 Overview of Trilinos Packages 8/22/2006

74 Trilinos Common Language: Petra § Petra provides a “common language” for distributed linear algebra objects (operator, matrix, vector) § Petra 1 provides distributed matrix and vector services. § Exists in basic form as an object model: w Describes basic user and support classes in UML, independent of language/implementation. w Describes objects and relationships to build and use matrices, vectors and graphs. w Has 3 implementations under development. 1 Petra is Greek for “foundation”. 8/22/2006

75 Petra Implementations § Three version under development: § Epetra (Essential Petra): w w Current production version. Restricted to real, double precision arithmetic. Uses stable core subset of C++ (circa 2000). Interfaces accessible to C and Fortran users. § Tpetra (Templated Petra): w Next generation C++ version. w Templated scalar and ordinal fields. w Uses namespaces, and STL: Improved usability/efficiency. § Jpetra (Java Petra): w Pure Java. Portable to any JVM. w Interfaces to Java versions of MPI, LAPACK and BLAS via interfaces. Developers: § Mike Heroux, Rob Hoekstra, Alan Williams, Paul Sexton 8/22/2006

76 Epetra § § § § 8/22/2006 Basic Stuff: What you would expect. Variable block matrix data structures. Multivectors. Arbitrary index labeling. Flexible, versatile parallel data redistribution. Language support for inheritance, polymorphism and extensions. View vs. Copy.

77 Aztec. OO § Krylov subspace solvers: CG, GMRES, Bi-CGSTAB, … § Incomplete factorization preconditioners § Aztec is the workhorse solver at Sandia: w Extracted from the MPSalsa reacting flow code. w Installed in dozens of Sandia apps. w 1900+ external licenses. § Aztec. OO improves on Aztec by: w Using Epetra objects for defining matrix and RHS. w Providing more preconditioners/scalings. w Using C++ class design to enable more sophisticated use. § Aztec. OO interfaces allows: w Continued use of Aztec for functionality. w Introduction of new solver capabilities outside of Aztec. Developers: § Mike Heroux, Alan Williams, Ray Tuminaro 8/22/2006

78 IFPACK: Algebraic Preconditioners § Overlapping Schwarz preconditioners with incomplete factorizations, block relaxations, block direct solves. § Accept user matrix via abstract matrix interface (Epetra versions). § Uses Epetra for basic matrix/vector calculations. § Supports simple perturbation stabilizations and condition estimation. § Separates graph construction from factorization, improves performance substantially. § Compatible with Aztec. OO, ML, Amesos. Can be used by NOX and ML. Developers: § Marzio Sala, Mike Heroux 8/22/2006

79 Amesos § Interface to direct solver for distributed sparse linear systems § Challenges: w No single solver dominates w Different interfaces and data formats, serial and parallel w Interface often change between revisions § Amesos offers: w w A single, clear, consistent interface, to various packages Common look-and-feel for all classes Separation from specific solver details Use serial and distributed solvers; Amesos takes care of data redistribution Developers: § Ken Stanley, Marzio Sala, Tim Davis 8/22/2006

80 Calling Amesos Epetra_Linear. Problem( A, x, b); Amesos Afact; Amesos_Base. Solver* Solver = Afact. Create( “Klu”, Problem ) ; Solver->Symbolic. Factorization( ) ; Solver->Numeric. Factorization( ) ; Solver->Solve( ) ; 8/22/2006
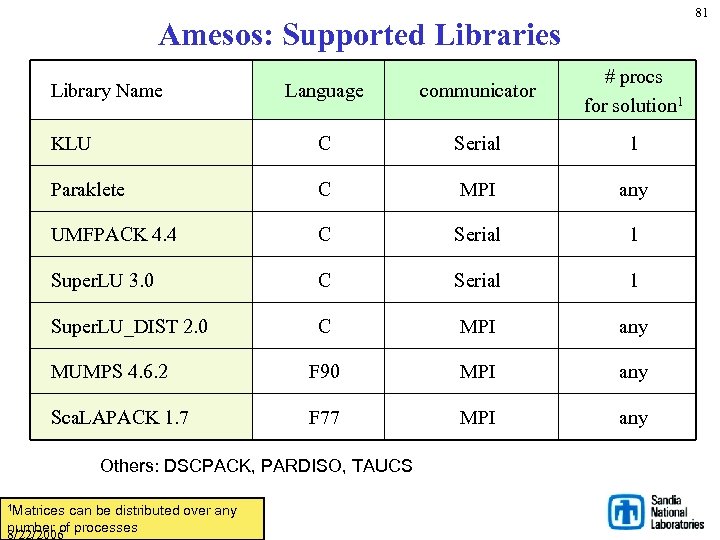
81 Amesos: Supported Libraries Language communicator # procs for solution 1 KLU C Serial 1 Paraklete C MPI any UMFPACK 4. 4 C Serial 1 Super. LU 3. 0 C Serial 1 Super. LU_DIST 2. 0 C MPI any MUMPS 4. 6. 2 F 90 MPI any Sca. LAPACK 1. 7 F 77 MPI any Library Name Others: DSCPACK, PARDISO, TAUCS 1 Matrices can be distributed over any number of processes 8/22/2006

82 ML: Multi-level Preconditioners § Smoothed aggregation, multigrid and domain decomposition preconditioning package § Critical technology for scalable performance of some key apps. § ML compatible with other Trilinos packages: w Accepts user data as Epetra_Row. Matrix object (abstract interface). Any implementation of Epetra_Row. Matrix works. w Implements the Epetra_Operator interface. Allows ML preconditioners to be used with Aztec. OO and TSF. § Can also be used completely independent of other Trilinos packages. Developers: § Ray Tuminaro, Jonathan Hu, Marzio Sala 8/22/2006

83 NOX: Nonlinear Solvers § Suite of nonlinear solution methods § NOX uses abstract vector and “group” interfaces: w Allows flexible selection and tuning of various strategies: • Directions. • Line searches. w Epetra/Aztec. OO/ML, LAPACK, PETSc implementations of abstract vector/group interfaces. § Designed to be easily integrated into existing applications. Developers: § Tammy Kolda, Roger Pawlowski 8/22/2006

84 LOCA § Library of continuation algorithms § Provides w w w w w Zero order continuation First order continuation Arc length continuation Multi-parameter continuation (via Henderson's MF Library) Turning point continuation Pitchfork bifurcation continuation Hopf bifurcation continuation Phase transition continuation Eigenvalue approximation (via ARPACK or Anasazi) Developers: § Andy Salinger, Eric Phipps 8/22/2006

85 Epetra. Ext: Extensions to Epetra § Library of useful classes not needed by everyone § § Most classes are types of “transforms”. Examples: w w w w w § Graph/matrix view extraction. Epetra/Zoltan interface. Explicit sparse transpose. Singleton removal filter, static condensation filter. Overlapped graph constructor, graph colorings. Permutations. Sparse matrix-matrix multiply. Matlab, Matrix. Market I/O functions. … Most classes are small, useful, but non-trivial to write. Developer: § Robert Hoekstra, Alan Williams, Mike Heroux 8/22/2006

86 Teuchos § Utility package of commonly useful tools: w w w Parameter. List class: key/value pair database, recursive capabilities. LAPACK, BLAS wrappers (templated on ordinal and scalar type). Dense matrix and vector classes (compatible with BLAS/LAPACK). FLOP counters, Timers. Ordinal, Scalar Traits support: Definition of ‘zero’, ‘one’, etc. Reference counted pointers, and more… § Takes advantage of advanced features of C++: w Templates w Standard Template Library (STL) § Parameter. List: w Allows easy control of solver parameters. Developers: § Roscoe Barlett, Kevin Long, Heidi Thorquist, Mike Heroux, Paul Sexton, Kris Kampshoff 8/22/2006

87 Belos and Anasazi § Next generation linear solvers (Belos) and eigensolvers (Anasazi) libraries, written in templated C++. § Provide a generic interface to a collection of algorithms for solving large-scale linear problems and eigenproblems. § Algorithm implementation is accomplished through the use of abstract base classes (mini interface). Interfaces are derived from these base classes to operator-vector products, status tests, and any arbitrary linear algebra library. § Includes block linear solvers and eigensolvers. Developers: §Heidi Thorquist, Mike Heroux, Chris Baker, Rich Lehoucq 8/22/2006

88 Kokkos § Goal: w Isolate key non-BLAS kernels for the purposes of optimization. § Kernels: w Dense vector/multivector updates and collective ops (not in BLAS/Teuchos). w Sparse MV, MM, SV, SM. § Serial-only for now. § Reference implementation provided (templated). § Mechanism for improving performance: w Default is aggressive compilation of reference source. w Be. BOP: Jim Demmel, Kathy Yelick, Rich Vuduc, UC Berkeley. w Vector version: Cray. Developer: § Mike Heroux 8/22/2006

89 New. Package § New. Package provides jump start to develop/integrate a new package § New. Package is a “Hello World” program and website: w Simple but it does work with autotools. w Compiles and builds. § New. Package directory contains: w w Commonly used directory structure: src, test, doc, example, config. Working autotools files. Documentation templates (doxygen). Working regression test setup. § Substantially cuts down on: w Time to integrate new package. w Variation in package integration details. w Development of website. 8/22/2006
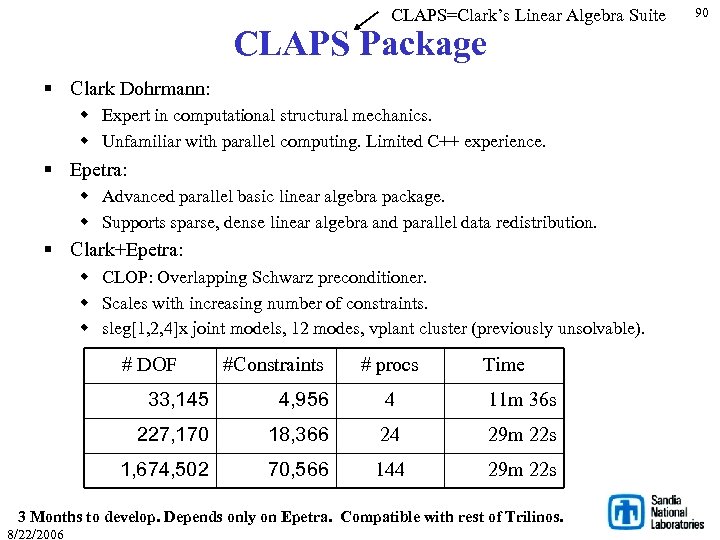
CLAPS=Clark’s Linear Algebra Suite CLAPS Package § Clark Dohrmann: w Expert in computational structural mechanics. w Unfamiliar with parallel computing. Limited C++ experience. § Epetra: w Advanced parallel basic linear algebra package. w Supports sparse, dense linear algebra and parallel data redistribution. § Clark+Epetra: w CLOP: Overlapping Schwarz preconditioner. w Scales with increasing number of constraints. w sleg[1, 2, 4]x joint models, 12 modes, vplant cluster (previously unsolvable). # DOF #Constraints # procs Time 33, 145 4, 956 4 11 m 36 s 227, 170 18, 366 24 29 m 22 s 1, 674, 502 70, 566 144 29 m 22 s 3 Months to develop. Depends only on Epetra. Compatible with rest of Trilinos. 8/22/2006 90

91 Pliris Package § § § § § Migration of Linpack benchmark code to supported environment. Used new_package as starting point. Put under source control for the first time. Portable build process for the first time. Documented distributed data model (Epetra). Has its own Bugzilla product, mail lists, regression tests. Source code browsable via Bonsai. And more… But Pliris is still an independent piece of code…and better off after the process. 8/22/2006

92 Interface Packages Thyra and Py. Trilinos 8/22/2006

93 template<class Scalar> bool silly. Cg. Solve( const Thyra: : Linear. Op. Base<Scalar> &A , const Thyra: : Vector. Base<Scalar> &b , const int max. Num. Iters , const typename Teuchos: : Scalar. Traits<Scalar>: : magnitude. Type tolerance , Thyra: : Vector. Base<Scalar>*x , std: : ostream *out = NULL ) { using Teuchos: : Ref. Count. Ptr; typedef Teuchos: : Scalar. Traits<Scalar> ST; // We need to use Scalar. Traits to support arbitrary types. typedef typename ST: : magnitude. Type Scalar. Mag; // This is the type returned from a vector norm. typedef one ST: : one()); // Get the vector space (domain and range spaces should be the same) Ref. Count. Ptr<const Thyra: : Vector. Space. Base<Scalar> > space = A. domain(); Thyra: silly. CGSolve § Generic CG code. § To use, provide: // Compute initial residual : r = b - A*x Ref. Count. Ptr<Thyra: : Vector. Base<Scalar> > r = create. Member(space); Thyra: : assign(&*r, b); // r = b Thyra: : apply(A, Thyra: : NOTRANS, *x, &* one, one); // r = -A*x + r const Scalar. Mag r 0_nrm = Thyra: : norm(*r); // Compute ||r 0|| = sqrt(<r 0, r 0>) for convergence test if(r 0_nrm == ST: : zero()) return true; // Trivial RHS and initial LHS guess? w Thyra: : Linear. Op. w Thyra: : Vector. § Works on any parallel machine. § Allows mixing of // Compute ||r|| = sqrt(<r, r>) // Converged to tolerance, Success! vectors matrices: // Create workspace vectors and scalars Ref. Count. Ptr<Thyra: : Vector. Base<Scalar> > p = create. Member(space), q = create. Member(space); Scalar rho_old; // Perform the iterations for( int iter = 0; iter <= max. Num. Iters; ++iter ) { // Check convergence and output iteration const Scalar. Mag r_nrm = Thyra: : norm(*r); if( r_nrm/r 0_nrm < tolerance ) return true; w PETSc & Epetra. // Compute iteration const Scalar rho = space->scalar. Prod(*r, *r); // <r, r> -> rho if(iter==0) Thyra: : assign(&*p, *r); // r -> p (iter == 0) else Thyra: : Vp_V( &*p, *r, Scalar(rho/rho_old) ); // r+(rho/rho_old)*p -> p (iter > 0) Thyra: : apply(A, Thyra: : NOTRANS, *p, &*q); // A*p -> q const Scalar alpha = rho/space->scalar. Prod(*p, *q); // rho/<p, q> -> alpha Thyra: : Vp_St. V( x, Scalar(+alpha), *p ); // +alpha*p + x -> x Thyra: : Vp_St. V( &*r, Scalar(-alpha), *q ); // -alpha*q + r -> r rho_old = rho; // rho-> rho_old (remember rho for next iter) } return false; // Failure } // end silly. Cg. Solve § Works with any scalar datatype. 8/22/2006

94 Py. Trilinos § Py. Trilinos provides Python access to Trilinos packages. § Uses SWIG to generate bindings. § Epetra, Aztec. OO, IFPACK, ML, NOX, LOCA, Amesos and New. Package are support. § Possible to: w Define Row. Matrix implementation in Python. w Use from Trilinos C++ code. § Performance for large grain is equivalent to C++. § Several times hit for very fine grain code. 8/22/2006
#include "mpi. h" #include "Epetra_Mpi. Comm. h" #include "Epetra_Vector. h" #include "Epetra_Time. h" #include "Epetra_Row. Matrix. h" #include "Epetra_Crs. Matrix. h" #include "Epetra_Time. h" #include "Epetra_Linear. Problem. h" #include "Trilinos_Util_Crs. Matrix. Gallery. h" using namespace Trilinos_Util; int main(int argc, char *argv[]) { MPI_Init(&argc, &argv); Epetra_Mpi. Comm(MPI_COMM_WORLD); int nx = 1000; int ny = 1000 * Comm. Num. Proc(); Crs. Matrix. Gallery("laplace_2 d", Comm); Gallery. Set("ny", ny); Gallery. Set("nx", nx); Gallery. Set("problem_size", nx*ny); Gallery. Set("map_type", "linear"); Epetra_Linear. Problem* Problem = Gallery. Get. Linear. Problem(); assert (Problem != 0); // retrieve pointers to solution (lhs), right-hand side (rhs) // and matrix itself (A) Epetra_Multi. Vector* lhs = Problem->Get. LHS(); Epetra_Multi. Vector* rhs = Problem->Get. RHS(); Epetra_Row. Matrix* A = Problem->Get. Matrix(); Epetra_Time(Comm); for (int i = 0 ; i < 10 ; ++i) A->Multiply(false, *lhs, *rhs); cout << Time. Elapsed. Time() << endl; MPI_Finalize(); return(EXIT_SUCCESS); } // end of main() 8/22/2006 95 C++ vs. Python: Equivalent Code #! /usr/bin/env python from Py. Trilinos import Epetra, Triutils Epetra. Init() Comm = Epetra. Py. Comm() nx = 1000 ny = 1000 * Comm. Num. Proc() Gallery = Triutils. Crs. Matrix. Gallery("laplace_2 d", Comm) Gallery. Set("nx", nx) Gallery. Set("ny", ny) Gallery. Set("problem_size", nx * ny) Gallery. Set("map_type", "linear") Matrix = Gallery. Get. Matrix() LHS = Gallery. Get. Starting. Solution() RHS = Gallery. Get. RHS() Time = Epetra. Time(Comm) for i in xrange(10): Matrix. Multiply(False, LHS, RHS) print Time. Elapsed. Time() Epetra. Finalize()

96 Templates and Generic Programming 8/22/2006

97 Investment in Generic Programming § 2 nd Generation Trilinos packages are templated on: w Ordinal. Type (think int). w Scalar. Type (think double). § Examples: Teuchos: : Serial. Dense. Matrix<int, double> A; Teuchos: : Serial. Dense. Matrix<short, float> B; § Scalar/Ordinal Traits mechanism completes support for genericity. § The following packages support templates: Teuchos (Basic Tools) Thyra (Abstract Interfaces) Tpetra (including MPI support) Belos (Krylov and Block Krylov Linear), IFPACK (algebraic preconditioners, next version), Anasazi (Eigensolvers), 8/22/2006

98 Potential Benefits of Templated Types Templated scalar (and ordinal) types have great potential: § Generic: Algorithms expressed over abstract field. § High Performance: Partial template specialization + Fortran. § Facilitate variety of algorithmic studies. § Allow study of asymptotic behavior of discretizations. § Facilitate debugging: Reduces FP error as source error. § Use your imagination… § All new Trilinos packages are templated. 8/22/2006
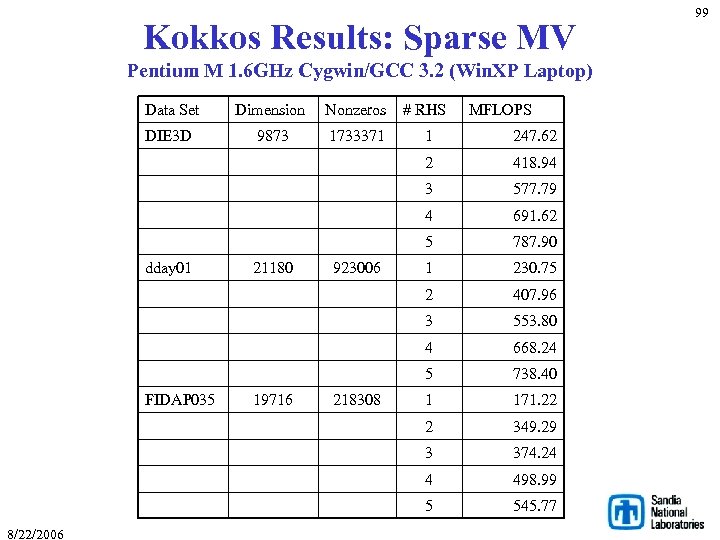
Kokkos Results: Sparse MV Pentium M 1. 6 GHz Cygwin/GCC 3. 2 (Win. XP Laptop) Data Set Dimension Nonzeros # RHS DIE 3 D 9873 1733371 1 247. 62 2 418. 94 3 577. 79 4 691. 62 5 787. 90 1 230. 75 2 407. 96 3 553. 80 4 668. 24 5 738. 40 1 171. 22 2 349. 29 3 374. 24 4 498. 99 5 545. 77 dday 01 FIDAP 035 8/22/2006 21180 19716 923006 218308 MFLOPS 99

100 ARPREC § The ARPREC library uses arrays of 64 -bit floating-point numbers to represent high-precision floating-point numbers. § ARPREC values behave just like any other floating-point datatype, except the maximum working precision (in decimal digits) must be specified before any calculations are done w mp: : mp_init(200); § Illustrate the use of ARPREC with an example using Hilbert matrices. 8/22/2006

101 Hilbert Matrices § A Hilbert matrix HN is a square N-by-N matrix such that: § For Example: 8/22/2006

102 Hilbert Matrices § Notoriously ill-conditioned w w w κ(H 3) 524 κ(H 5) 476610 κ(H 10) 1. 6025 x 1013 κ(H 20) 7. 8413 x 1017 κ(H 100) 1. 7232 x 1020 § Hilbert matrices introduce large amounts of error 8/22/2006
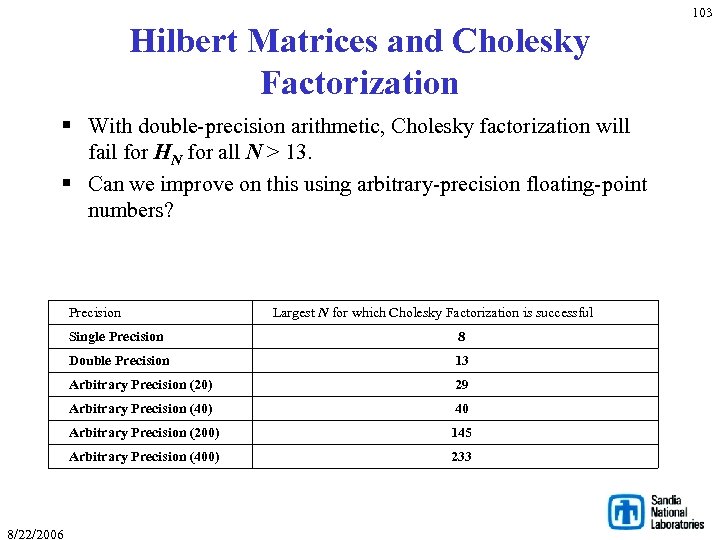
103 Hilbert Matrices and Cholesky Factorization § With double-precision arithmetic, Cholesky factorization will fail for HN for all N > 13. § Can we improve on this using arbitrary-precision floating-point numbers? Precision Largest N for which Cholesky Factorization is successful Single Precision Double Precision 13 Arbitrary Precision (20) 29 Arbitrary Precision (40) 40 Arbitrary Precision (200) 145 Arbitrary Precision (400) 8/22/2006 8 233

104 New Trilinos 7. 0 Packages 8/22/2006

105 Galeri & Isorropia § Galeri: Generates Epetra maps and matrices for testing. w A set of functionalities that are very close to that of the MATLAB's gallery() function. w Capabilities to create several well-know finite difference matrices. w A simple finite element code that can be used to discretize scalar second order elliptic problems using Galerkin and SUPG techniques, on both 2 D and 3 D unstructured grids. § Isorropia: Repartitioning/rebalancing. w Assists with redistributing objects such as: • • 8/22/2006 Matrices and matrix-graphs in a parallel execution setting. Allows for more efficient computations. Primarily an interface to the Zoltan library. Can be built and used with minimal capability without Zoltan.

106 Moertel & Moocho § Moertel: w Capabilities for nonconforming mesh tying and contact formulations in 2 and 3 dimensions using Mortar methods. w Mortar methods are types of Lagrange Multiplier constraints that can be used in contact formulations and in non-conforming or conforming mesh tying as well as in domain decomposition techniques. w Used in a large class of nonconforming situations such as the surface coupling of different physical models, discretization schemes or non-matching triangulations along interior interfaces of a domain. § MOOCHO: (Multifunctional Object-Oriented ar. CHitecture for Optimization) w Large-scale invasive simultaneous analysis and design (SAND) using primarily SQP-related methods. 8/22/2006

107 RTOp & Rythmos § RTOp: (reduction/transformation operators) w Provides basic mechanism for implementing vector operations in a flexible and efficient manner. § Rythmos: ODE/DAE. w Includes: backward Euler, forward Euler, explicit Runge-Kutta, and implicit BDF at this time. w Native support for operator split methods. w Highly modular. w Forward sensitivity computations will be included in the first release with adjoint sensitivities coming in near future. 8/22/2006

108 Web. Trilinos § Web. Trilinos: Web interface to Trilinos w w 8/22/2006 Generate test problems or read from file. Generate C++ or Python code fragments and click-run. Hand modify code fragments and re-run. Will use during hands-on.

109 Dynamic External Package Support § New directory Trilinos/packages/external. § Supports seamless integration of externally developed packages via package registration. § Completes the goal of Trilinos-compatibility. 8/22/2006

110 Software Quality 8/22/2006

111 SQA/SQE § Software Quality Assurance/Engineering is important. § No longer sufficient to say “We do a good job”. § Trilinos facilitates SQA/SQE development/processes for packages: w 32 of 47 ASCI SQE practices are directly handled by Trilinos (no requirements on packages). w Trilinos provides significant support for the remaining 15. w Trilinos Dev Guide Part II: Specific to ASCI requirements. w Trilinos software engineering policies provide a ready-made infrastructure for new packages. w Trilinos philosophy: Few requirements. Instead mostly suggested practices. Provides package with option to provide alternate process. 8/22/2006
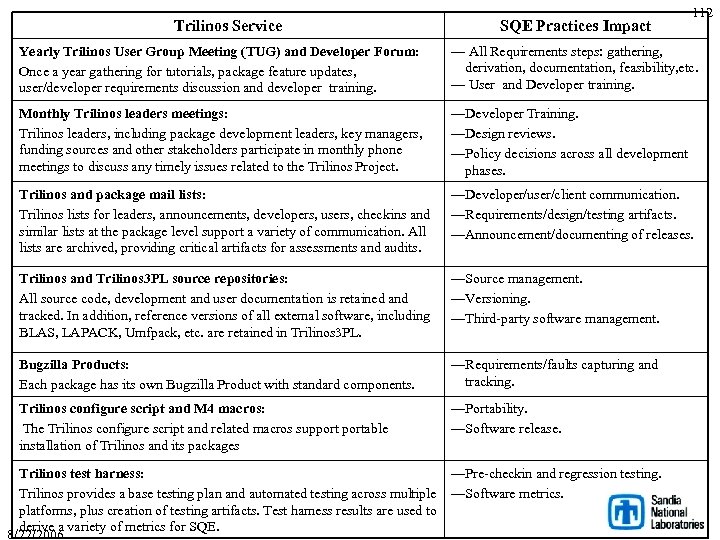
Trilinos Service SQE Practices Impact 112 Yearly Trilinos User Group Meeting (TUG) and Developer Forum: Once a year gathering for tutorials, package feature updates, user/developer requirements discussion and developer training. — All Requirements steps: gathering, derivation, documentation, feasibility, etc. — User and Developer training. Monthly Trilinos leaders meetings: Trilinos leaders, including package development leaders, key managers, funding sources and other stakeholders participate in monthly phone meetings to discuss any timely issues related to the Trilinos Project. —Developer Training. —Design reviews. —Policy decisions across all development phases. Trilinos and package mail lists: Trilinos lists for leaders, announcements, developers, users, checkins and similar lists at the package level support a variety of communication. All lists are archived, providing critical artifacts for assessments and audits. —Developer/user/client communication. —Requirements/design/testing artifacts. —Announcement/documenting of releases. Trilinos and Trilinos 3 PL source repositories: All source code, development and user documentation is retained and tracked. In addition, reference versions of all external software, including BLAS, LAPACK, Umfpack, etc. are retained in Trilinos 3 PL. —Source management. —Versioning. —Third-party software management. Bugzilla Products: Each package has its own Bugzilla Product with standard components. —Requirements/faults capturing and tracking. Trilinos configure script and M 4 macros: The Trilinos configure script and related macros supportable installation of Trilinos and its packages —Portability. —Software release. Trilinos test harness: —Pre-checkin and regression testing. Trilinos provides a base testing plan and automated testing across multiple —Software metrics. platforms, plus creation of testing artifacts. Test harness results are used to derive a variety of metrics for SQE. 8/22/2006

113 The Trilinos Tutorial Package § Trilinos is large (and still growing…) w More than 600 K code lines w Many packages • a lot of functionalities… • … and also a lot to learn § What is the best way for a new user to learn Trilinos? § Using a Trilinos package of course: Didasko! 8/22/2006

114 What DIDASKO is not § DIDASKO, as a tutorial, cannot cover the most advanced features of Trilinos: w Only the “stable” features are covered § DIDASKO is not a substitute of each package’s documentation and examples, which remain of fundamental importance 8/22/2006

115 Covered Packages § At present, we cover Epetra Teuchos NOX Anasazi 8/22/2006 Triutils Aztec. OO Amesos Tpetra IFPACK ML Epetra. Ext

116 Trilinos Availability/Information § § Trilinos and related packages are available via LGPL. Current release (6. 0) is “click release”. Unlimited availability. Trilinos Release 7: September 2006. Trilinos Awards: w w 2004 R&D 100 Award. SC 2004 HPC Software Challenge Award. Sandia Team Employee Recognition Award. Lockheed-Martin Nova Award Nominee. § More information: w http: //software. sandia. gov/trilinos w Additional documentation at my website: http: //www. cs. sandia. gov/~mheroux. § 4 th Annual Trilinos User Group Meeting: November 7 -9, 2006 at SNL. 8/22/2006

117 Summary § Trilinos package model provides a welcoming environment for solver developers: w w Extremely flexible. Building up package, not making it conform. Scalable growth model for complex multi-physics solver suites. Working toward full vertical coverage of capabilities. § Basic principles can be applied to any similar “project of projects”: w Modularity w Interfaces w Common infrastructure. § Trilinos new_package is self-contained software environment: w Package and website useful to any project wanting to ramp up in use of standard tools. w Available separately, Open Source. w Used by groups outside of Trilinos as well as within. 8/22/2006

118 Trilinos Might be of Interest to you if… § Your application includes non-PDE equations. § Multiple RHS, Block Krylov linear, eigen solvers, SAND needed. § You develop an independent Trilinos-compatible solver. § Interested in multi-physics. § App is in C++. § Interested in collaborating on Fortran interface. § Unstructured Data redistribution is important. § Multi-precision useful. § Parallel Python interest. 8/22/2006

119 Extras 8/22/2006

Algorithms Research: Truly Useful Multi-level Methods § Fly-through of next 4 slides. § Theme: Multi-level preconditioning has come of age across broad spectrum of problems. 8/22/2006 120
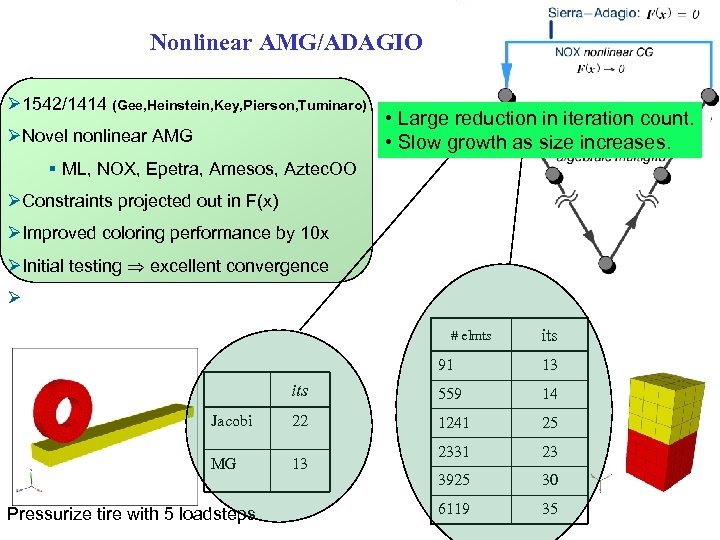
Nonlinear AMG/ADAGIO Ø 1542/1414 (Gee, Heinstein, Key, Pierson, Tuminaro) ØNovel nonlinear AMG • Large reduction in iteration count. • Slow growth as size increases. § ML, NOX, Epetra, Amesos, Aztec. OO ØConstraints projected out in F(x) ØImproved coloring performance by 10 x ØInitial testing excellent convergence Ø # elmts its 91 13 its 559 14 Jacobi 22 1241 25 MG 13 2331 23 3925 30 6119 35 Pressurize tire with 5 loadsteps
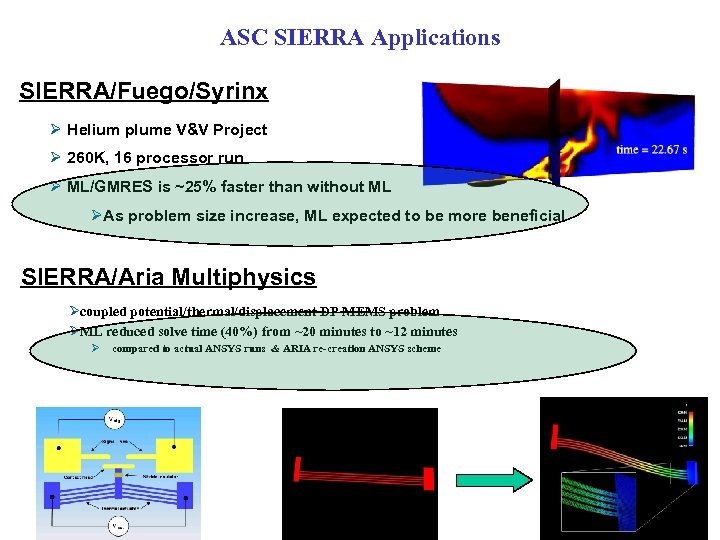
ASC SIERRA Applications SIERRA/Fuego/Syrinx Ø Helium plume V&V Project Ø 260 K, 16 processor run Ø ML/GMRES is ~25% faster than without ML ØAs problem size increase, ML expected to be more beneficial SIERRA/Aria Multiphysics Øcoupled potential/thermal/displacement DP MEMS problem ØML reduced solve time (40%) from ~20 minutes to ~12 minutes Ø compared to actual ANSYS runs & ARIA re-creation ANSYS scheme

Premo premo (Latin) – to squeeze (compress) Compressible flow to determine aerodynamic characteristics for the Nuclear Weapons Complex § Additional Issues that have been addressed w FEI/Nox/Trilinos interface development w Block Algorithm Improvements w Block Gauss-Seidel, Block Grid Transfers § § B 61 problem (6. 5 million dofs, 64 procs) Pseudo-transient + Newton Euler flow, Mach. 8 Linear solver: 173 solves, tolerance= 10 -4 § § GMRES/ILU 7494 sec GMRES/MG 3704 sec § Numerical Issues w nonlinear path, time step path, setup time, linear sys. difficulty 123

Premo premo (Latin) – to squeeze (compress) § § Falcon problem (13+ Million dofs, 150 procs) Pseudo-transient + Newton Euler flow, Mach. 75 Linear solver: 109 solves, tolerance= 10 -4 § § GMRES/ILU 7620 sec GMRES/MG 3787 sec 10 x improvement on final linear solve. > 5 x gains on some problems over entire sequence § New Grid Transfers (220+K Falcon, 1 proc) § § Pseudo-transient + Newton, Euler flow @ Mach. 75 Last linear solve, tolerance= 10 -9 § GMRES/MG/old transfers 47 its, 49 sec § GMRES/MG/new transfers 24 its, 26 sec 124

125 Multi-level Methods Summary § Solving hard, real problems fast, scalably. § Still need more… 8/22/2006

Algorithms Research: Specialized Solvers § Next wave of capabilities: Specialized solvers. § Examples in Trilinos: w Optimal domain decomposition preconditioners for structures: CLAPS w Mortar methods for interface coupling: Moertel. w Segregated Preconditioners for Navier-Stokes: Meros. § Examples in Applications: w EMU (with Boeing). w Tramonto. 8/22/2006 126
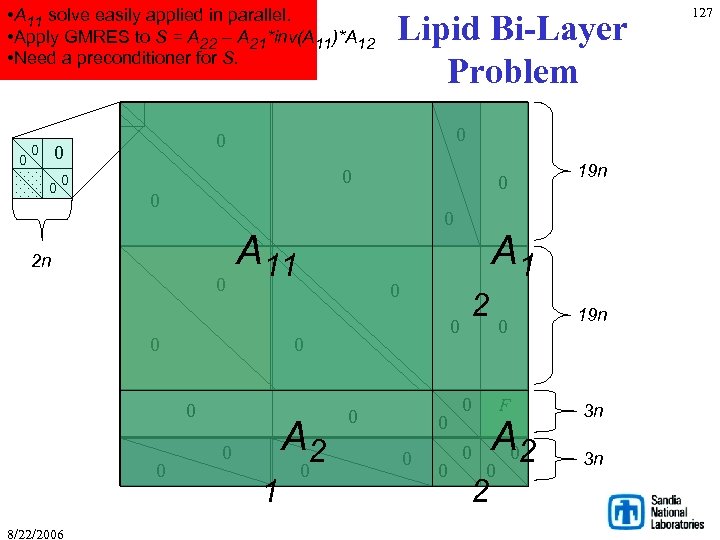
• A 11 solve easily applied in parallel. • Apply GMRES to S = A 22 – A 21*inv(A 11)*A 12 • Need a preconditioner for S. 0 0 0 0 0 2 n 0 0 0 0 A 11 0 8/22/2006 Lipid Bi-Layer Problem A 2 0 1 0 0 0 19 n A 1 2 0 0 0 F A 02 0 2 19 n 3 n 3 n 127

128 Preconditioner for S A 22 = A 22 = 8/22/2006 D 11 F D 21 D 11 F 0 D 21 • D 11, D 22 = O(1), D 21 = O(1 e-10) • Ignore D 21 for preconditioning. • P(S) requires • 2 diagonal scalings, • matvec with F. • All distributed operations.

129 Tramonto Solver Summary § 3 -level linear operator structure. § Matlab to fully parallel: 1 month. § Complex orchestration: w Preconditioner: 100+ distributed Epetra matrices used in sequence. w ML, IFPACK, Amesos used on subproblems. § Utilizes 8 Trilinos packages in total. § 566 Lines of Code (Polymer Solver). § Polymorphic Design. 8/22/2006

3 D Polymer Results Approximately Linear Performance Improvement For Fixed Size Problem Same Iteration Counts as Processor Count Increases 130

131 Properties of New Solver § Uniform distributed mesh → uniform distributed work. § Preconditioner sub-steps naturally parallel: → Results invariant to processor count up to round-off. § Preconditioner requires almost no extra memory: → 4 -10 X reduction over previous approach. § GMRES subspace and storage reduced 6 X-10 X or more. Laurie’s Favorite Properties! § Speedup 20 -2 X. § Solver has: w No tuning parameters. w Near linear scaling. Michael A. Heroux, Laura J. D. Frink, and Andrew G. Salinger. Schur complement based approaches to solving density functional theories for inhomogeneous fluids on parallel computers. SIAM J. Sci. Comput. Submitted. 8/22/2006

132 Specialized Solver API: EMU § § § § EMU: Peridynamics modeling code. Boeing: Modeling of composite material failure. Onset to failure: Explicit time stepping. Prior to onset: Desire implicit (large-time step). Previous capability: Serial Y 12 M. Present: Trilinos serial and (almost) parallel. Status: w Solver API production-ready (290 LOC). w Serial results complete. w Parallel soon (requires work in EMU also). § First results (smallest problem): 3. 5 X faster (complete run). 8/22/2006

133 Specialized Solvers Summary § Trilinos: Rich, configurable foundation w Parallel data model. w Large and growing collection of solvers in scalable package framework. § Specialized solvers: Next-level advances w Exploit inherent problem properties. w Few Lines of Code: Leverage Trilinos. w Robust, scalable, efficient. Michael A. Heroux. A Solver-Independent API for multi-DOF Applications using Trilinos. Int. J. of Computational Science and Engineering. Submitted. 8/22/2006
41840e95439e5db1fe892b4c2997a1a4.ppt