1 Теорема об изменении количества движения точки Количеством

1. Теорема об изменении количества движения точки Количеством движения точки называется векторная величина (1)

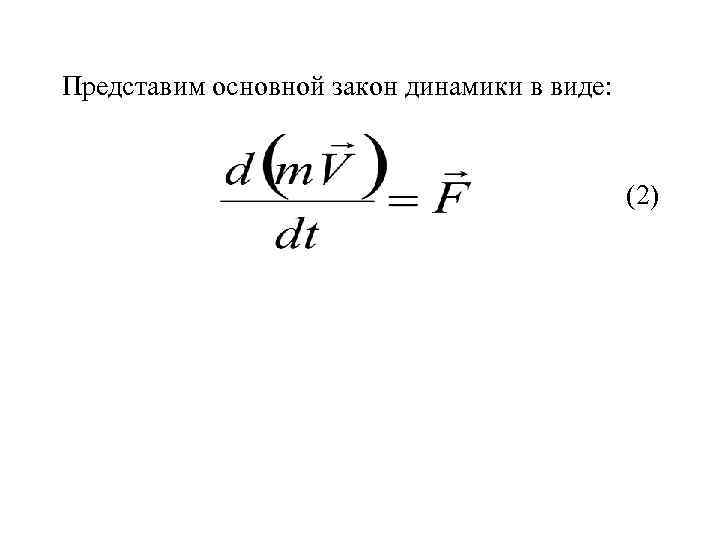
Представим основной закон динамики в виде: (2)

Представим основной закон динамики в виде: (2) или

Представим основной закон динамики в виде: (2) или (3) - элементарный импульс силы

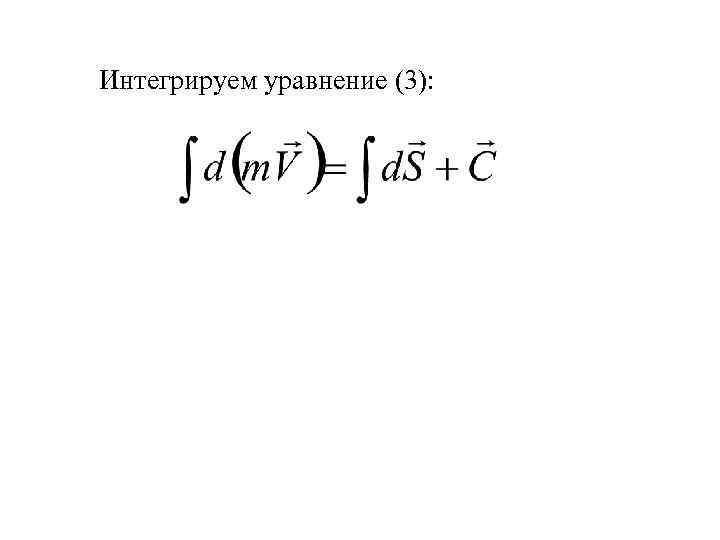
Интегрируем уравнение (3):

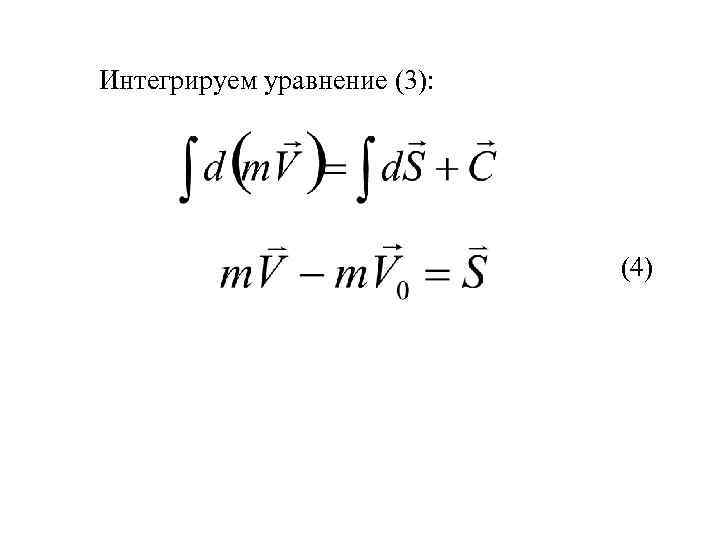
Интегрируем уравнение (3): (4)

Интегрируем уравнение (3): (4) Изменение количества движения точки за некоторый промежуток времени равняется импульсу действующих на точку сил за тот же промежуток времени

Пример: Точка массой , двигаясь прямолинейно под действием постоянной силы , изменила свою скорость на в течение промежутка времени. Определить силу.

Решение:

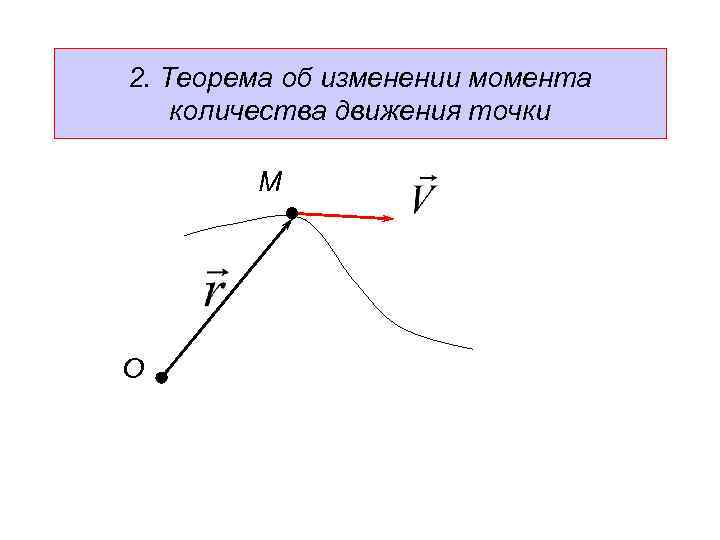
2. Теорема об изменении момента количества движения точки М О

Умножим уравнение (2) слева на радиус-вектор

Умножим уравнение (2) слева на радиус-вектор или (5) -момент количества движения (кинетический момент) точки относительно центра О

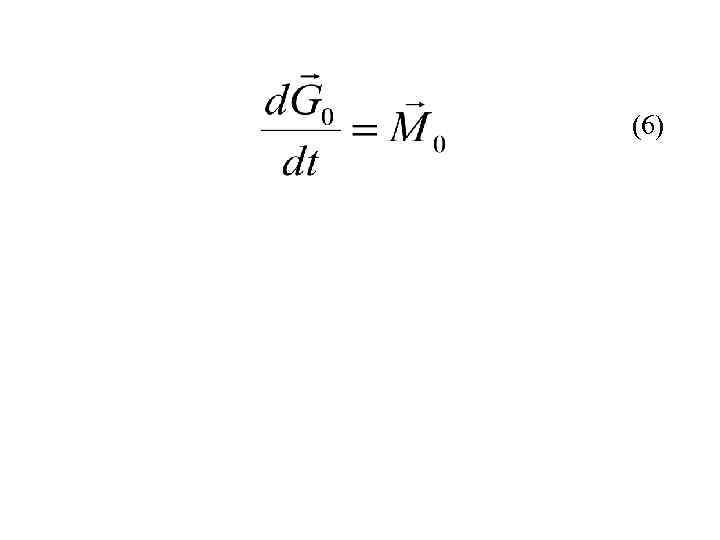
(6)

(6) Производная по времени момента количества движения точки относительно какого-либо центра равна моменту действующих на точку сил относительно того же центра.

Пример: Точка М движется вокруг неподвижного центра по эллипсу под действием силы притяжения к этому центру. Найти скорость точки в наиболее удаленной от центра точке траектории, если ее скорость в наиболее близком к нему положении , а наибольший радиус в 5 раз больше наименьшего.

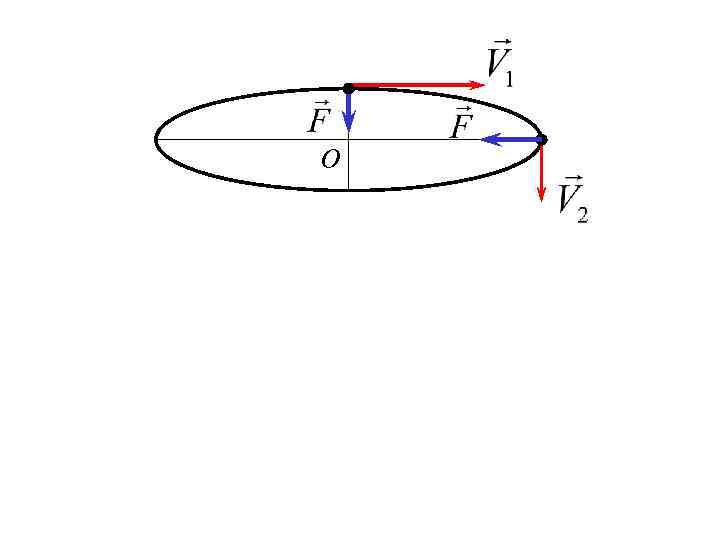
О

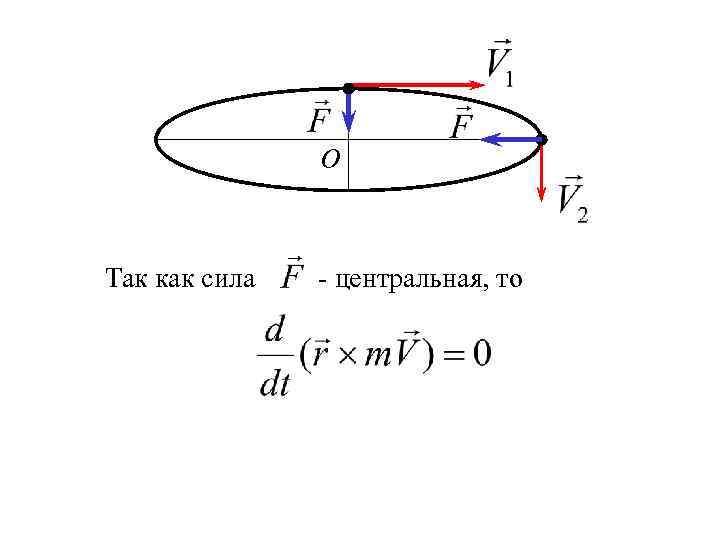
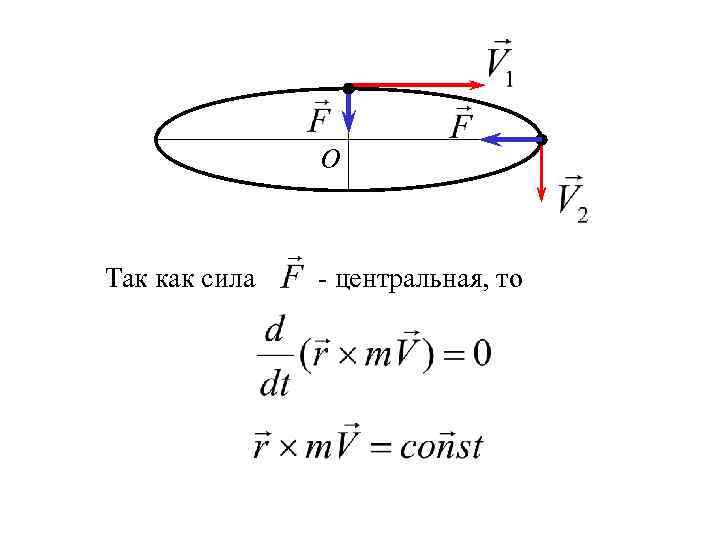
О Так как сила - центральная, то

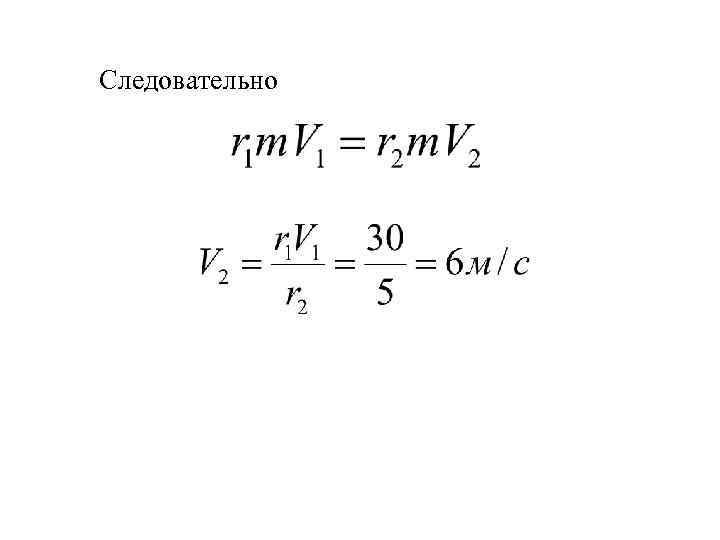
Следовательно

3. Теорема об изменении кинетической энергии точки Кинетической энергией точки называется скалярная величина (7)

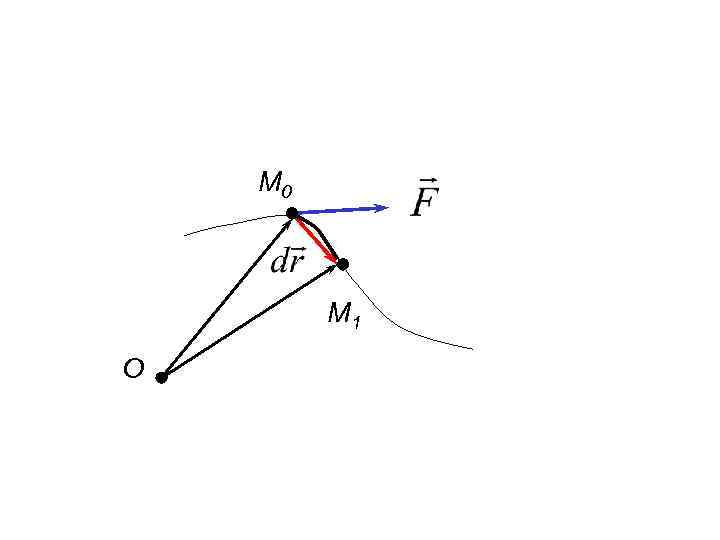
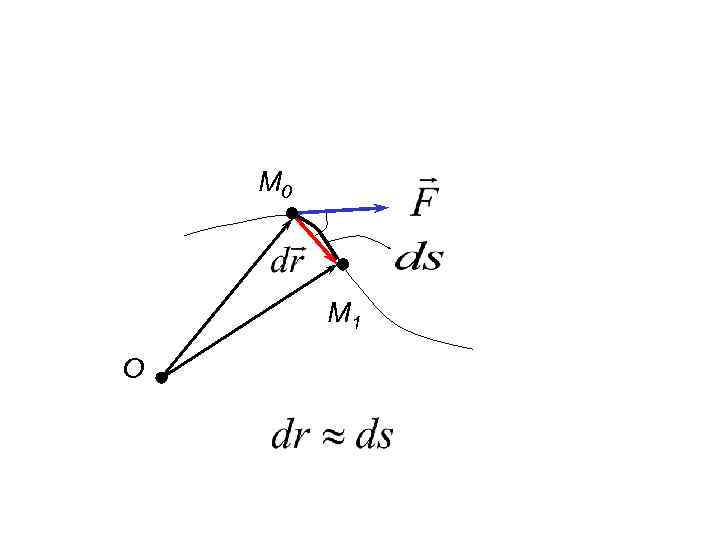
М 0 М 1 О

Элементарной работой силы, совершенной на перемещении называется скалярное произведение (8) - не всегда является полным дифференциалом

Элементарной работой силы, совершенной на перемещении называется скалярное произведение (8) - не всегда является полным дифференциалом (9)

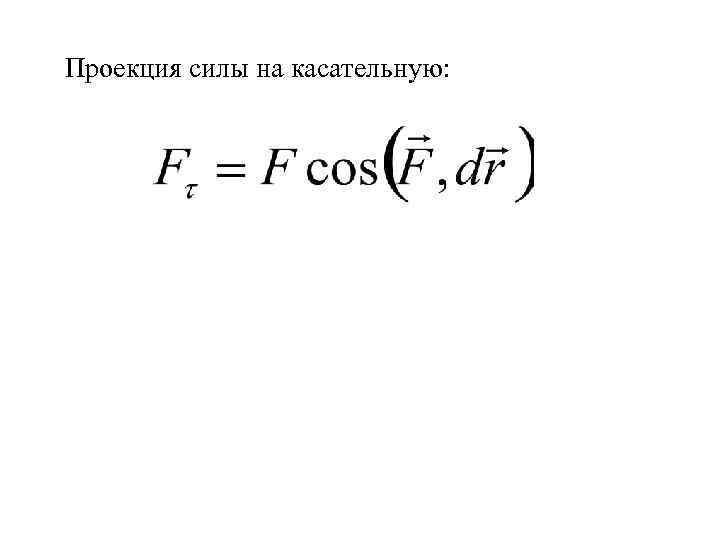
Проекция силы на касательную:

Проекция силы на касательную: Работа силы на конечном перемещении по кривой М 0 М 1 (10)

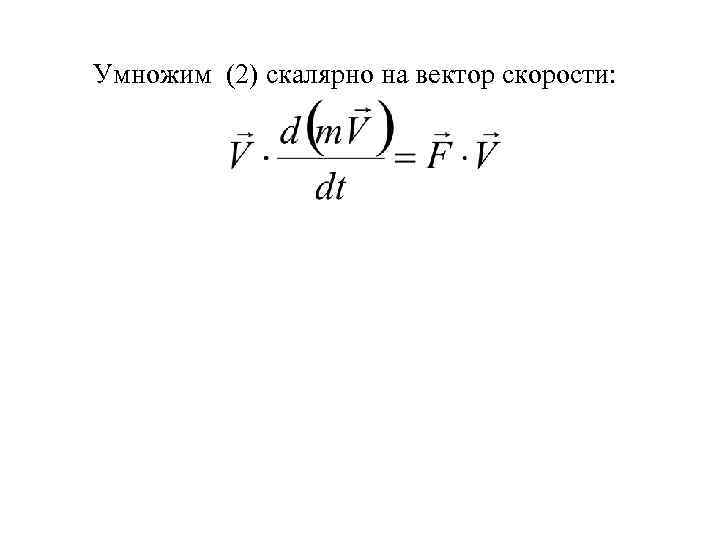
Умножим (2) скалярно на вектор скорости:

Умножим (2) скалярно на вектор скорости: или

(11) Интегральная форма: (12)

(11) Интегральная форма: (12) Изменение кинетической энергии точки на некотором перемещении равно работе действующих на точку сил на том же перемещении.

Если работа силы представляет собой полный дифференциал некоторой функции:

Если работа силы представляет собой полный дифференциал некоторой функции: то из (11) следует

Если работа силы представляет собой полный дифференциал некоторой функции: то из (11) следует В результате интегрирования получим закон сохранения энергии: (13) П- потенциальная энергия точки, Е- полная энергия

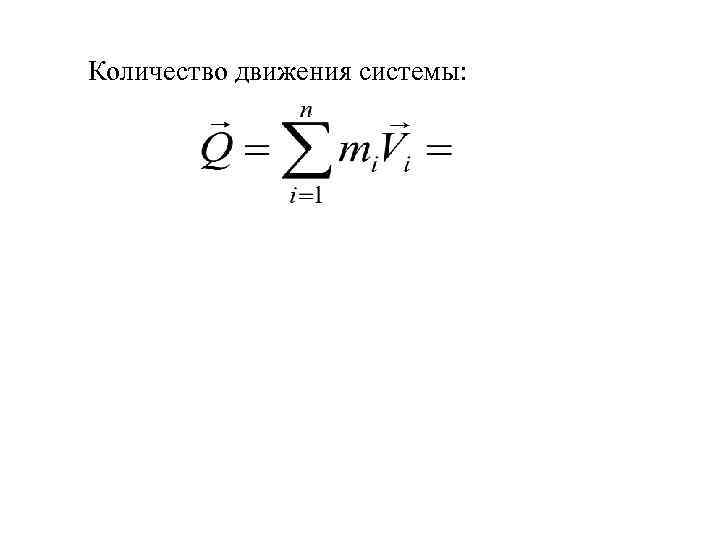
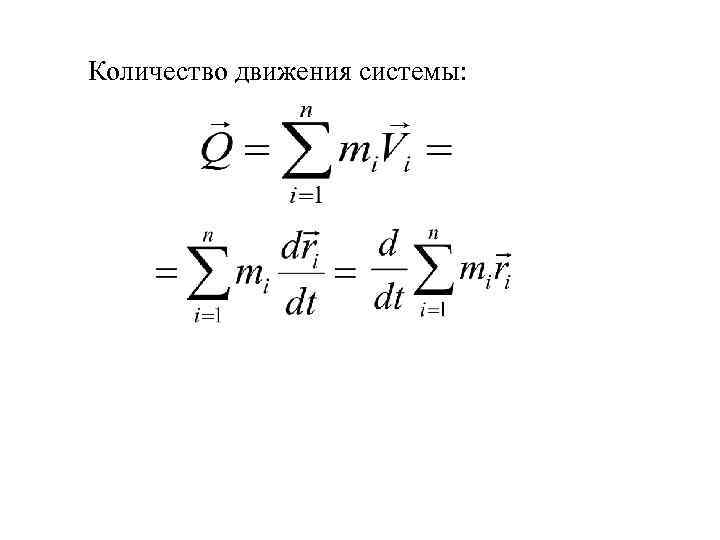
Количество движения системы:

Количество движения системы: Так как где М – масса всей системы

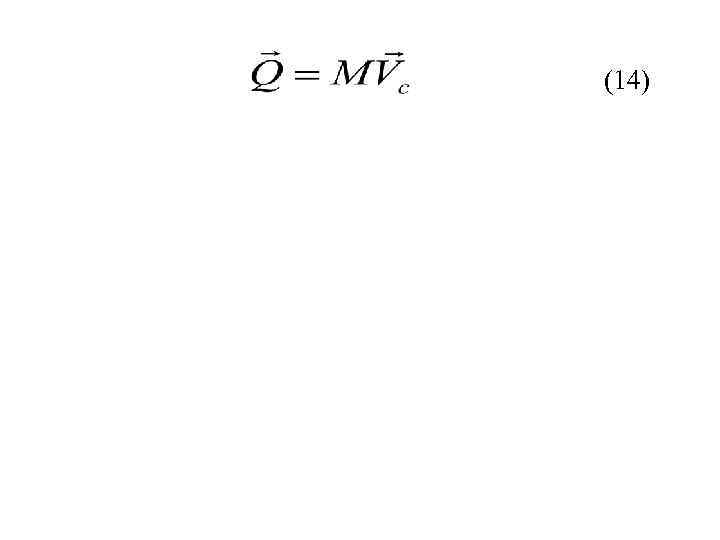
(14)

(14) Теорема о движении центра масс системы (15)

(14) Теорема о движении центра масс системы (15) (16) -главный вектор внешних сил, действующих на систему

Центр масс механической системы движется как материальная точка, на которую действуют все приложенные к системе внешние силы.

Центр масс механической системы движется как материальная точка, на которую действуют все приложенные к системе внешние силы. Если , то Следовательно, если на систему не действуют внешние силы (или их действие скомпенсировано), то центр масс системы движется прямолинейно и равномерно, либо находится в покое.

Теорема об изменении кинетического момента системы По аналогии с (6) (17)

Теорема об изменении кинетического момента системы По аналогии с (6) (17) Производная кинетического момента системы относительно некоторого неподвижного центра по времени равна моменту внешних сил, действующих на систему, относительно того же центра

Кинетический момент АТТ относительно оси вычисляется по формуле: (18) где Jx –момент инерции тела относительно оси Ox Момент инерции зависит от массы и формы тела.

При вращении АТТ вокруг оси имеем: (19) Дифференциальное уравнение вращательного движения АТТ вокруг оси: (20)

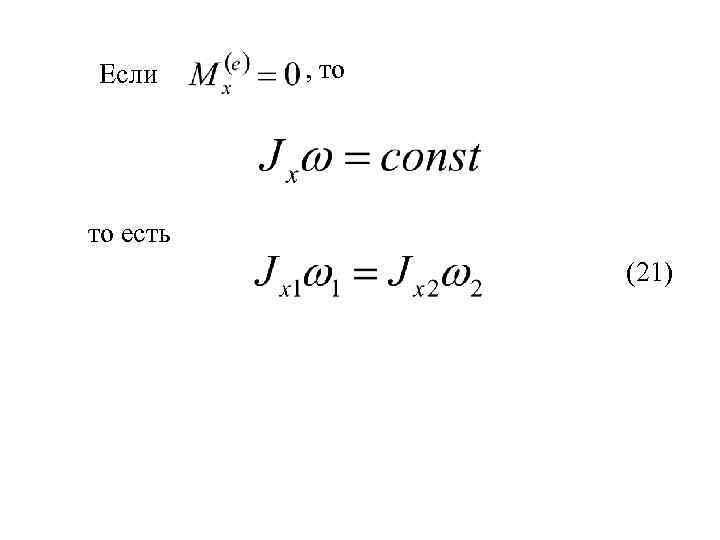
Если , то то есть (21)

Теорема об изменении кинетической энергии системы По аналогии с (12) (22) - работа внешних сил -работа внутренних сил

Если механическая система состоит из твердых тел, соединенных нерастяжимыми нитями, то работа внутренних сил равна нулю. Такие системы называются неизменяемыми. (23)