1 Структурное программирование на языке Паскаль Тема 2

1 Структурное программирование на языке Паскаль Тема 2. Проект © К. Ю. Поляков, 2007 -2009

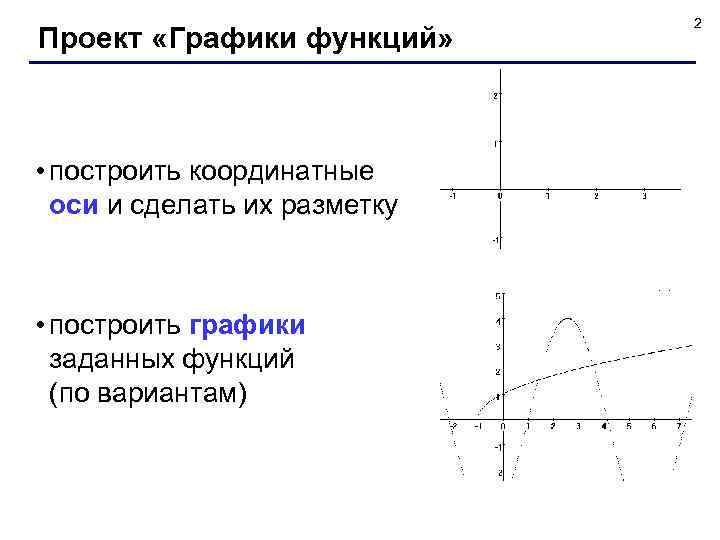Проект «Графики функций» • построить координатные оси и сделать их разметку • построить графики заданных функций (по вариантам) 2

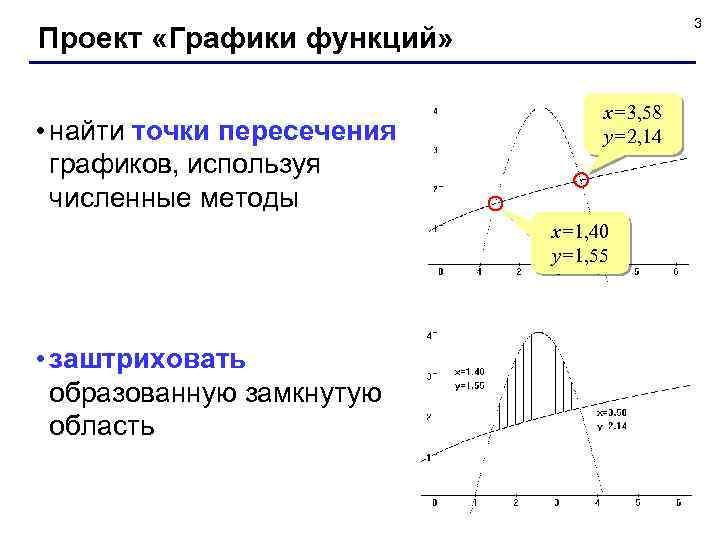3 Проект «Графики функций» • найти точки пересечения графиков, используя численные методы x=3, 58 y=2, 14 x=1, 40 y=1, 55 • заштриховать образованную замкнутую область

4 Проект «Графики функций» • вычислить площадь этой области двумя способами • оформить отчет по работе S 1=3, 014 S 2=3, 025

Структура программы program qq; константы и переменные процедуры и функции begin основная Axes; { оси координат } программа Plot; { графики функций } Cross; { точки пересечения графиков } Hatch; { штриховка } Area; { площадь (способ 1) } «заглушки» Area 2; { площадь (способ 2) } end. {------------------Axes: оси координат ------------------} procedure Axes; begin end; 5

6 Структурное программирование на языке Паскаль Тема 3. Графики функций © К. Ю. Поляков, 2007 -2009

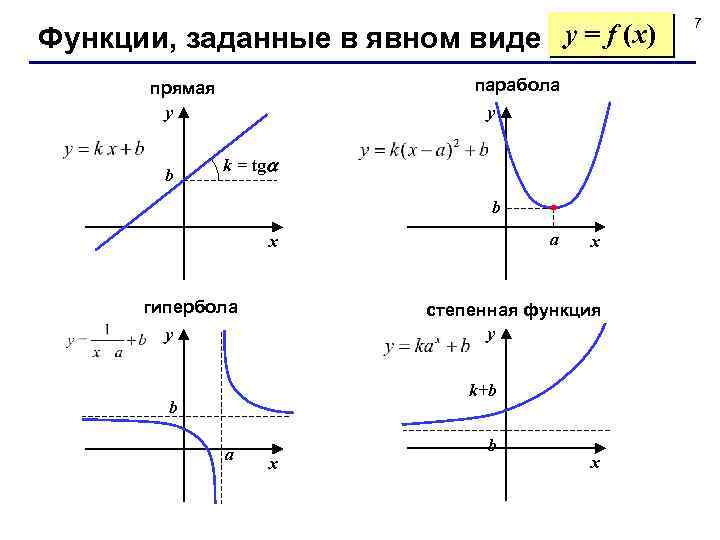Функции, заданные в явном виде y = f (x) парабола y прямая y b k = tg b a x гипербола y x степенная функция y k+b b a x b x 7

Функции, заданные в неявном виде f (x, y) = 0 пример: уравнение эллипса y a y 0 b x 0 x 8

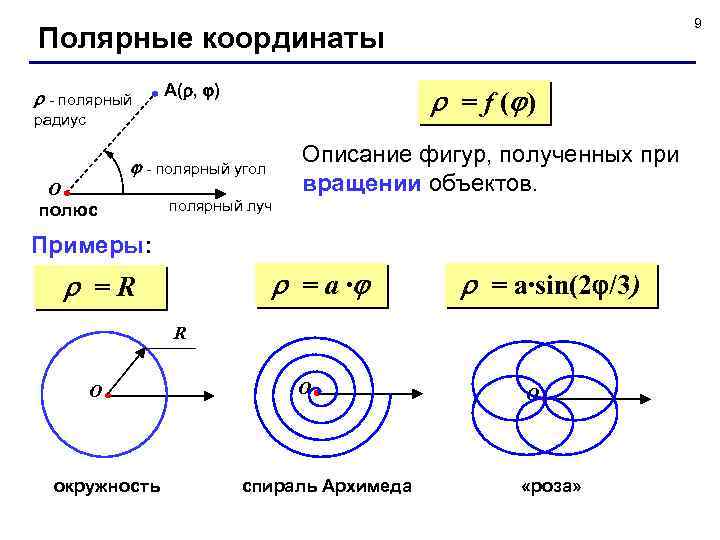9 Полярные координаты - полярный А( , ) = f ( ) радиус Описание фигур, полученных при вращении объектов. - полярный угол O полюс полярный луч Примеры: = a ∙ =R = a∙sin(2 /3) R O окружность O спираль Архимеда O «роза»

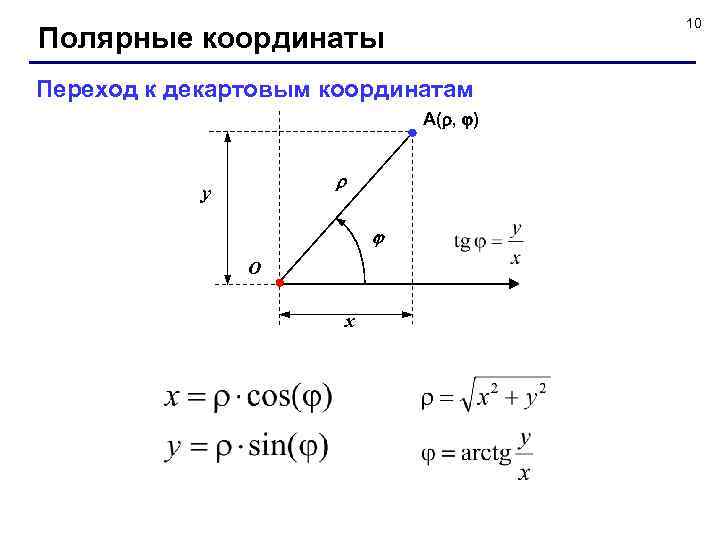10 Полярные координаты Переход к декартовым координатам А( , ) y O x

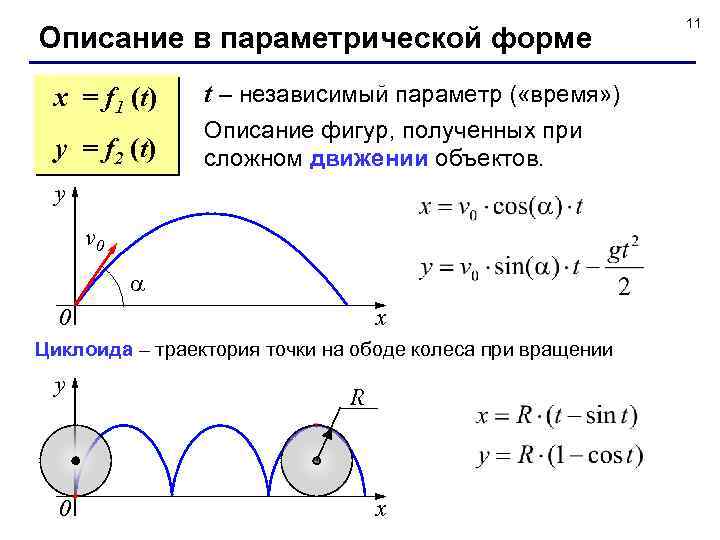Описание в параметрической форме x = f 1 (t) y = f 2 (t) t – независимый параметр ( «время» ) Описание фигур, полученных при сложном движении объектов. y v 0 x 0 Циклоида – траектория точки на ободе колеса при вращении y 0 R x 11

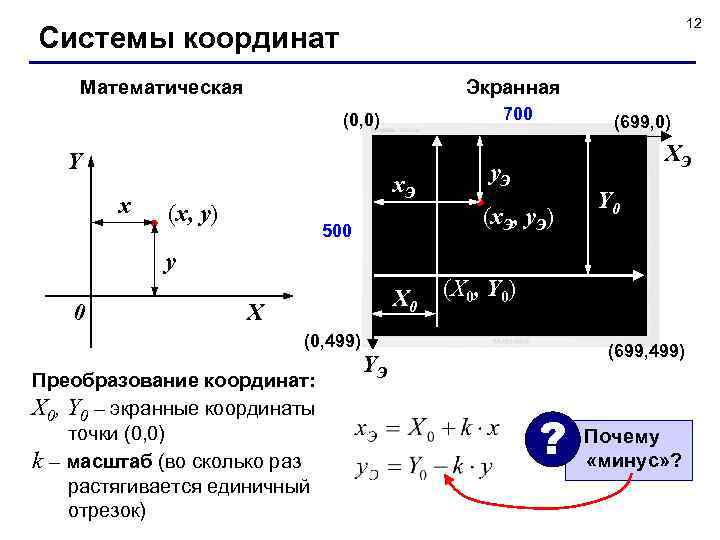12 Системы координат Экранная Математическая 700 (0, 0) Y x x. Э (x, y) (699, 0) XЭ y. Э (x. Э, y. Э) 500 Y 0 y 0 X (X 0, Y 0) (0, 499) Преобразование координат: X 0, Y 0 – экранные координаты точки (0, 0) k – масштаб (во сколько раз растягивается единичный отрезок) (699, 499) YЭ ? Почему «минус» ?

Перевод в экранные координаты const X 0 = 100; Y 0 = 400; { начало координат } k = 80; { масштаб } {---------------------Screen. X - перевод X в координаты экрана ----------------------} function Screen. X(x: real): integer; begin Screen. X : = round(X 0 + k*x); end; {-------------------Screen. Y – перевод Y в координаты экрана ----------------------} function Screen. Y(y: real): integer; begin Screen. Y : = round(Y 0 - k*y); end; ? Откуда берутся X 0, Y 0 и k? 13

14 Оси координат (0, 0) (699, 0) Y 0 X 0 (X 0, Y 0) (0, 499) procedure Axes; begin line ( X 0, 0, X 0, 499 ); line ( 0, Y 0, 699, Y 0 ); end; (699, 499)

Разметка оси X ( «черточки» ) x. Э (x. Э, Y 0− 2) Y 0 Число меток на [0, xmax]: длина 700 – X 0 единичный отрезок k (x. Э, Y 0+2) X 0 700 − X 0 15 trunc – отбросить дробную часть var i, xe: integer; … for i: =1 to trunc((700 -X 0)/k) do begin xe : = Screen. X(i); line ( xe, Y 0 -2, xe, Y 0+2 ); end;

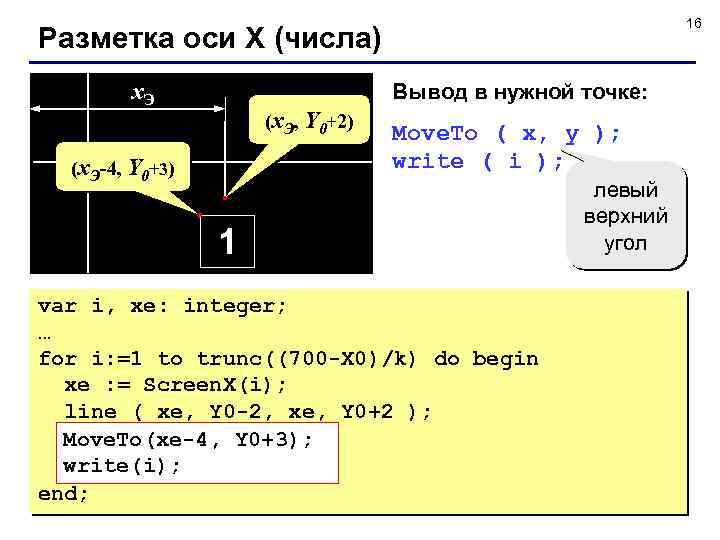16 Разметка оси X (числа) x. Э Вывод в нужной точке: (x. Э, Y 0+2) (x. Э-4, Y 0+3) Move. To ( x, y ); write ( i ); 1 var i, xe: integer; … for i: =1 to trunc((700 -X 0)/k) do begin xe : = Screen. X(i); line ( xe, Y 0 -2, xe, Y 0+2 ); Move. To(xe-4, Y 0+3); write(i); end; левый верхний угол

Оси с разметкой (полностью) procedure Axes; var i, xe: integer; begin line ( X 0, 0, X 0, 499 ); line ( 0, Y 0, 699, Y 0 ); for i: =1 to trunc((700 -X 0)/k) do begin xe : = Screen. X(i); line ( xe, Y 0 -2, xe, Y 0+2 ); Move. To(xe-4, Y 0+3); write(i); end; 17

Задания « 4» : Сделать разметку осей полностью (не только положительной части оси X). « 5» : Сделать задание на « 4» , использовав только 2 цикла (1 цикл для каждой оси). ! Разметка должна работать правильно при любых значениях X 0 и Y 0. 18

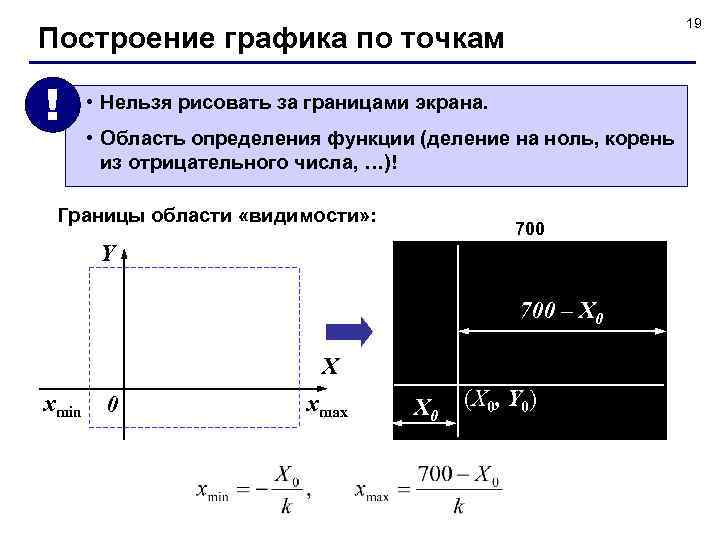19 Построение графика по точкам ! • Нельзя рисовать за границами экрана. • Область определения функции (деление на ноль, корень из отрицательного числа, …)! Границы области «видимости» : 700 Y 700 – X 0 X xmin 0 xmax X 0 (X 0, Y 0)

Вывод точки с проверкой {--------------------Set. Point - вывод пикселя с проверкой и пересчетом координаты в --------------------} математической системе procedure Set. Point ( x, y: real; r, g, b: integer); var xe, ye: integer; цвет точки begin xe : = Screen. X(x); ye : = Screen. Y(y); if (xe >= 0) and (xe < 700) and (ye >= 0) and (ye < 500) then begin Pen(1, r, g, b); если точка (x. Э, y. Э) Point(xe, ye); в пределах end; экрана… end; 20

Описание функций {--------------------F 1, F 2 Вход: x Выход: y = f 1(x), f 2(x) ---------------------} function f 1 (x: real): real; begin f 1 : = sqrt(x+1); end; function f 2 (x: real): real; begin f 2 : = 4*sin(x-1); end; 21

Области определения Для {--------------------ODZ 1 – область определения f 1(x) Вход: x Выход: True, если x входит в ОДЗ False, если x не входит в ОДЗ --------------------} function odz 1(x: real): Boolean; begin odz 1 : = (x >= -1); end; Для не нужно! 22

23 Вывод графика функции {--------------------PLOT вывод графиков функций --------------------} procedure Plot; границы var xmin, xmax, x, h: real; видимой begin части xmin : = - X 0 / k; xmax : = (700 - X 0) / k; шаг по x h : = (xmax - xmin) / 1000; x : = xmin; while x <= xmax do begin if odz 1(x) then Set. Point(x, f 1(x), 255, 0, 0); x : = x + h; end; Почему не for? Что плохо? end; ? ?

Общее расположение function f 1(x: real): real; begin. . . end; function odzf 1(x: real): Boolean; begin. . . end; procedure Set. Point ( x, y: real; r, g, b: integer); begin. . . end; procedure Plot; begin. . . if odz 1(x) then Set. Point(x, f 1(x), 255, 0, 0); . . . end; 24

Задания « 4» : Построить графики в соответствии с заданием. « 5» : Построить графики, соединив точки линиями. 25

26 Структурное программирование на языке Паскаль Тема 4. Точки пересечения © К. Ю. Поляков, 2007 -2009

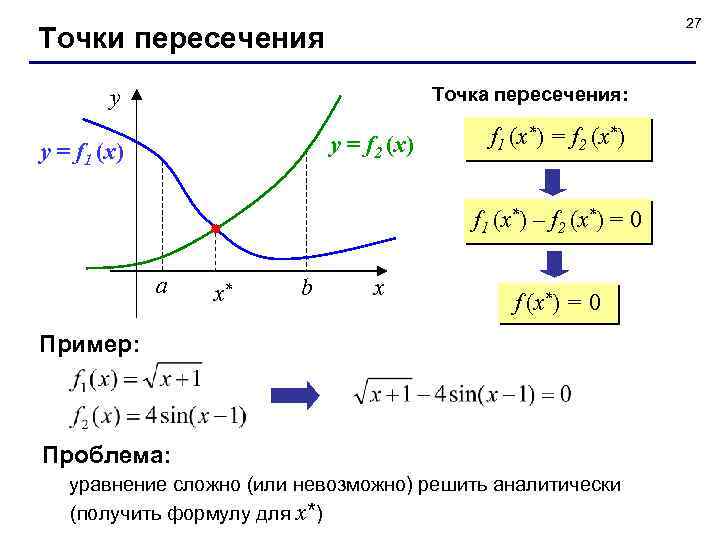27 Точки пересечения Точка пересечения: y y = f 2 (x) y = f 1 (x) f 1 (x*) = f 2 (x*) f 1 (x*) – f 2 (x*) = 0 a x* b x f (x*) = 0 Пример: Проблема: уравнение сложно (или невозможно) решить аналитически (получить формулу для x*)

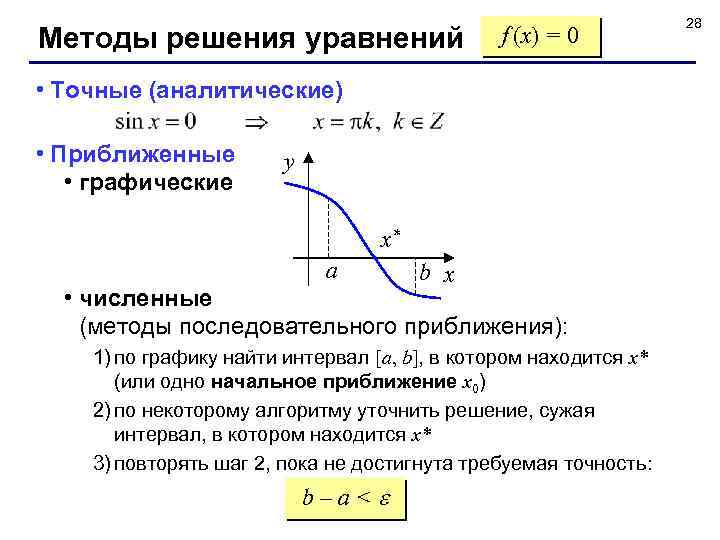Методы решения уравнений f (x) = 0 • Точные (аналитические) • Приближенные • графические y x* a b x • численные (методы последовательного приближения): 1) по графику найти интервал [a, b], в котором находится x* (или одно начальное приближение x 0) 2) по некоторому алгоритму уточнить решение, сужая интервал, в котором находится x* 3) повторять шаг 2, пока не достигнута требуемая точность: b–a< 28

Численные методы Применение: используются тогда, когда точное (аналитическое) решение неизвестно или очень трудоемко. • дают хотя бы какое-то решение • во многих случаях можно оценить ошибку и найти решение с заданной точностью • решение всегда приближенное, неточное 29

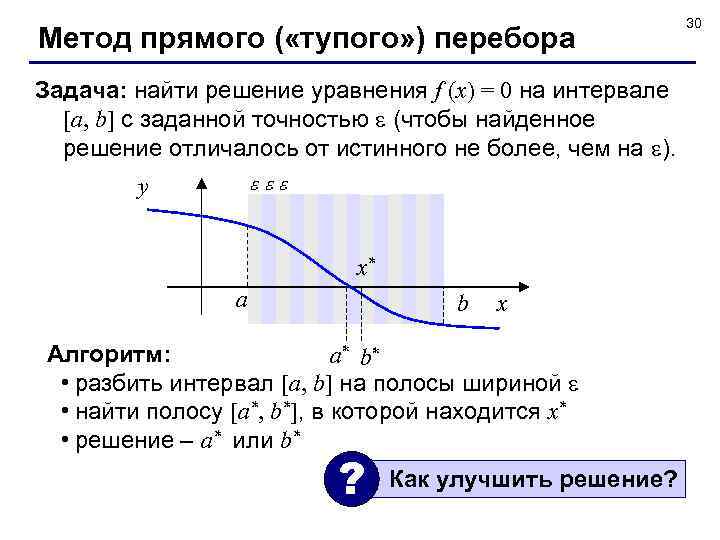Метод прямого ( «тупого» ) перебора Задача: найти решение уравнения f (x) = 0 на интервале [a, b] с заданной точностью (чтобы найденное решение отличалось от истинного не более, чем на ). y x* a b x Алгоритм: a* b* • разбить интервал [a, b] на полосы шириной • найти полосу [a*, b*], в которой находится x* • решение – a* или b* ? Как улучшить решение? 30

31 Есть ли решение на [a, b]? есть решение y y нет решения x* a ! y нет решения x* bx a b x x* Если непрерывная функция f (x) имеет разные знаки на концах интервала [a, b], то в некоторой точке x* внутри [a, b] она равна 0, то есть f (x*) = 0! x

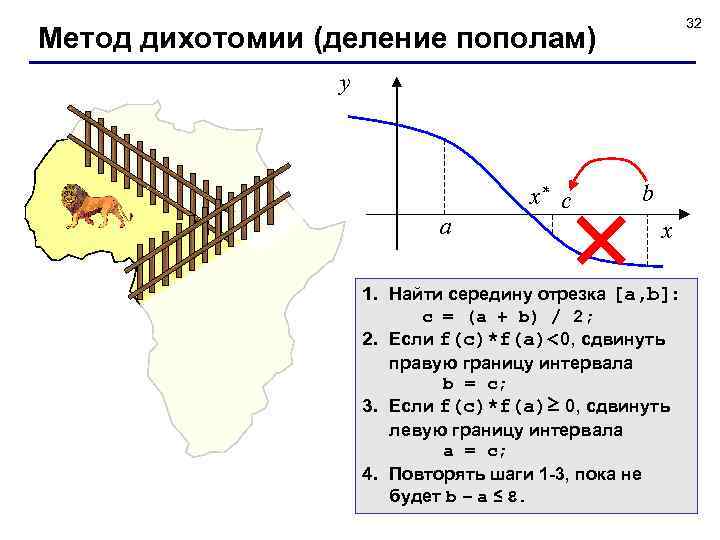32 Метод дихотомии (деление пополам) y a x* с b x 1. Найти середину отрезка [a, b]: c = (a + b) / 2; 2. Если f(c)*f(a)<0, сдвинуть правую границу интервала b = c; 3. Если f(c)*f(a)≥ 0, сдвинуть левую границу интервала a = c; 4. Повторять шаги 1 -3, пока не будет b – a ≤ .

Метод дихотомии (деления пополам) • простота • можно получить решение с любой заданной точностью • нужно знать интервал [a, b] • на интервале [a, b] должно быть только одно решение • большое число шагов для достижения высокой точности • только для функций одной переменной 33

Метод дихотомии (в программе) {-----------------------Solve находит точку пересечения на [a, b] Вход: a, b – границы интервала, a < b eps - точность решения Выход: x – решение уравнения f 1(x)=f 2(x) -----------------------} function Solve(a, b, eps: real): real; var c, fa, fc: real; begin while b - a > eps do begin c : = (a + b) / 2; fa : = f 1(a) - f 2(a); fc : = f 1(c) - f 2(c); if fa*fc < 0 then b : = c else a : = c; end; Solve : = (a + b) / 2; end; 34

Метод дихотомии (в программе) 35 var xc 1, xc 2: real; { глобальные переменные } { абсциссы точек пересечения }. . . function Solve(a, b, eps: real): real; begin. . . end; найти решение на интервале [1, 2] с procedure Cross; точностью 0, 0001 begin Solve ( 2, 0. 0001); xc 1 : = Solve(1, 1, 2, 0. 0001 ); Move. To(150, 220); вывод на экран значения x … write(xc 1: 5: 2); Move. To(150, 240); … и значения y! write(f 1(xc 1): 5: 2); . . . то же самое для end; остальных точек

36 Структурное программирование на языке Паскаль Тема 5. Штриховка © К. Ю. Поляков, 2007 -2009

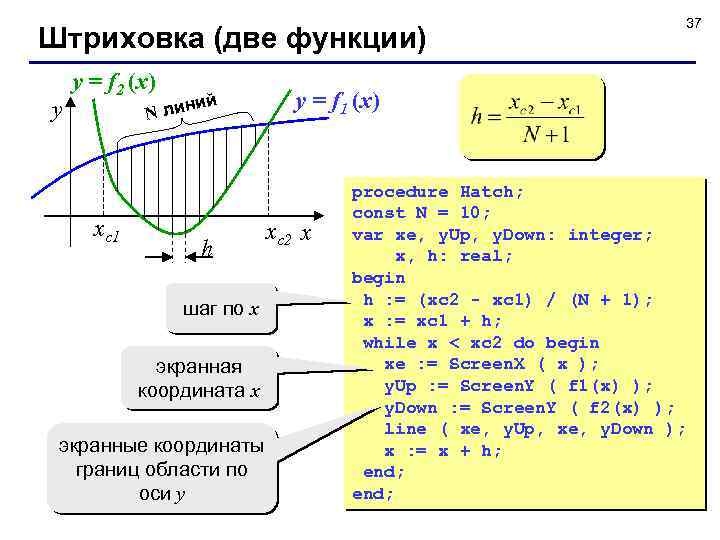Штриховка (две функции) y y = f 2 (x) ий N лин xс1 h шаг по x экранная координата x экранные координаты границ области по оси y 37 y = f 1 (x) xс2 x procedure Hatch; const N = 10; var xe, y. Up, y. Down: integer; x, h: real; begin h : = (xc 2 - xc 1) / (N + 1); x : = xc 1 + h; while x < xc 2 do begin xe : = Screen. X ( x ); y. Up : = Screen. Y ( f 1(x) ); y. Down : = Screen. Y ( f 2(x) ); line ( xe, y. Up, xe, y. Down ); x : = x + h; end;

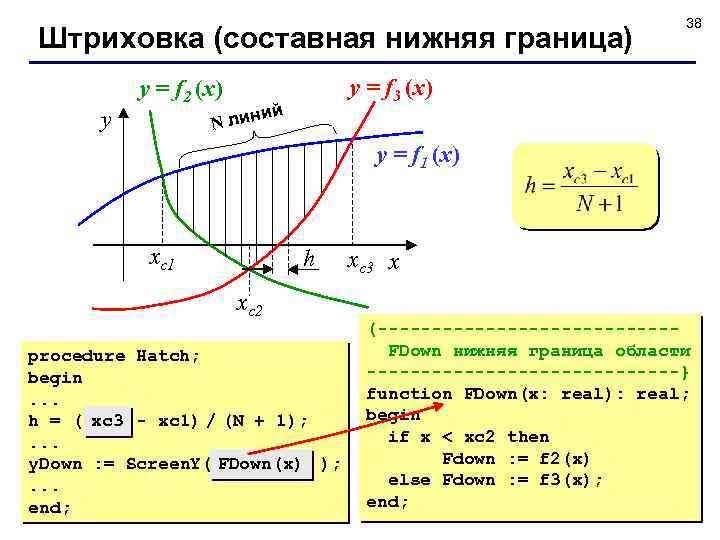Штриховка (составная нижняя граница) y y = f 2 (x) 38 y = f 3 (x) ий N лин y = f 1 (x) xс1 h xс2 procedure Hatch; begin. . . h = ( xc 3 - xc 1) / (N + 1); . . . y. Down : = Screen. Y( FDown(x) ); . . . end; xс3 x (--------------FDown нижняя граница области ---------------} function FDown(x: real): real; begin if x < xc 2 then Fdown : = f 2(x) else Fdown : = f 3(x); end;

Штриховка (общий случай) function FUp (x: real): real; . . . function FDown (x: real): real; . . . у всех по-разному… procedure Hatch; . . . h : = ( xc 3 ? xc 1 ) / (N + 1); x : = xc 1 + h; xc 3 do begin while x < ? xe : = Screen. X ( x ); y. Up : = Screen. Y ( FUp(x) ); ? y. Down : = Screen. Y ( FDown(x) ); ? line ( xe, y. Up, xe, y. Down ); x : = x + h; end; 39

40 Структурное программирование на языке Паскаль Тема 6. Вычисление площади © К. Ю. Поляков, 2007 -2009

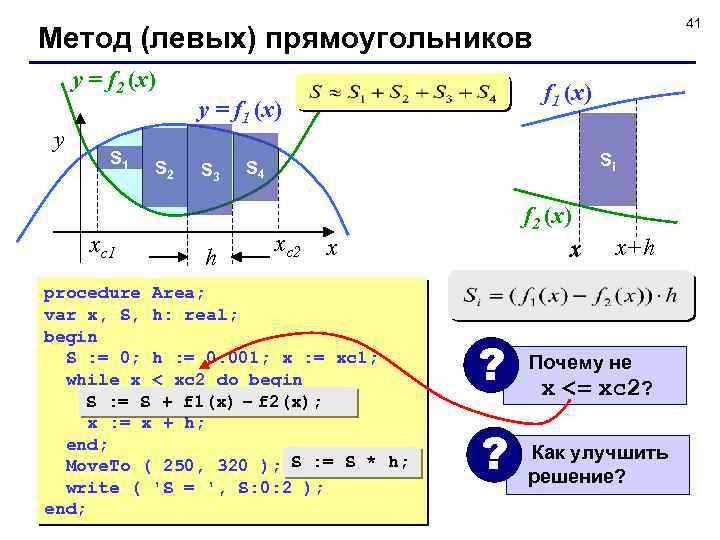41 Метод (левых) прямоугольников y = f 2 (x) y S 1 xс1 S 2 f 1 (x) y = f 1 (x) S 3 h Si S 4 xс2 f 2 (x) x x procedure Area; var x, S, h: real; begin S : = 0; h : = 0. 001; x : = xc 1; while x < xc 2 do begin h*(f 1(x)-f 2(x)); S : = S + f 1(x) – f 2(x); x : = x + h; end; Move. To ( 250, 320 ); S : = S * h; write ( 'S = ', S: 0: 2 ); end; ? ? x+h Почему не x <= xc 2? Как улучшить решение?

42 Метод (правых) прямоугольников y = f 2 (x) y S 1 xс1 S 2 f 1 (x) y = f 1 (x) S 3 h Si S 4 xс2 x procedure Area; var x, S, h: real; begin S : = 0; h : = 0. 001; x : = xc 1; while x < xc 2 do begin S : = S + f 1(x+h) – f 2(x+h); h*(f 1(x+h)-f 2(x+h)); x : = x + h; end; Move. To ( 250, 320 ); S : = S * h; write ( 'S = ', S: 0: 2 ); end; f 2 (x) x x+h

43 Метод (средних) прямоугольников y = f 2 (x) y S 1 xс1 S 2 y = f 1 (x) S 3 h f 1 (x) S 4 Si f 2 (x) xс2 x x procedure Area; var x, S, h: real; begin S : = 0; h : = 0. 001; x : = xc 1; while x < xc 2 do begin S : = S + f 1(x+h/2) – f 2(x+h/2); x : = x + h; end; Move. To ( 250, 320 ); S : = S * h; write ( 'S = ', S: 0: 2 ); end; ? x+h Какой метод точнее? левые (правые): средние

44 Метод трапеций y = f 2 (x) y S 1 xс1 S 2 f 1 (x) y = f 1 (x) S 3 h Si S 4 xс2 x f 2 (x) x x+h x = xc 1; S : =( x < xc 2 do begin while f 1(xc 1)-f 2(xc 1)+f 1(xc 2)-f 2(xc 2) )/2; x. S: = S + f 1(x) – f 2(x) : = xc 1 + h; Как улучшить? + xc 2 do – f 2(x+h); while x

45 Метод Монте-Карло Применение: вычисление площадей сложных фигур (трудно применить другие методы). Требования: необходимо уметь достаточно просто определять, попала ли точка (x, y) внутрь фигуры. Пример: заданы 100 кругов (координаты центра, радиусы), которые могу пересекаться. Найти площадь области, перекрытой кругами. ? Как найти S?

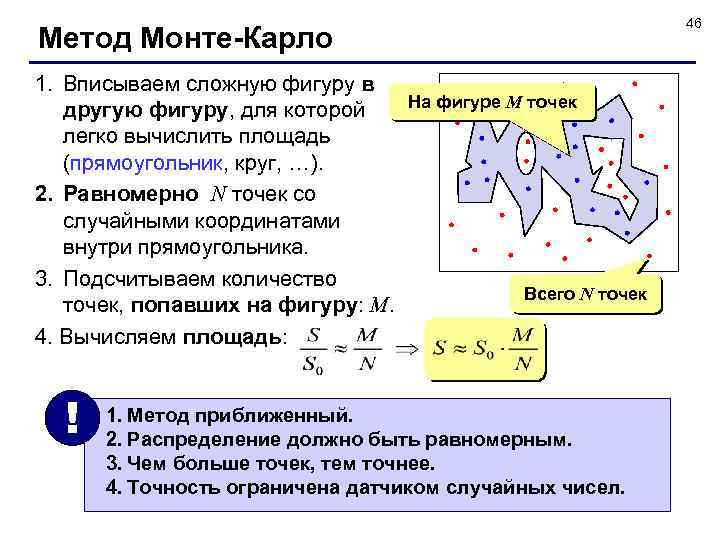46 Метод Монте-Карло 1. Вписываем сложную фигуру в другую фигуру, для которой легко вычислить площадь (прямоугольник, круг, …). 2. Равномерно N точек со случайными координатами внутри прямоугольника. 3. Подсчитываем количество точек, попавших на фигуру: M. 4. Вычисляем площадь: ! На фигуре M точек Всего N точек 1. Метод приближенный. 2. Распределение должно быть равномерным. 3. Чем больше точек, тем точнее. 4. Точность ограничена датчиком случайных чисел.

Случайное число в заданном интервале random [0, 1) (b-a)*random [0, b-a) (b-a)*random + a [a, b) {--------------------rand – случайное вещественное число в заданном интервале ---------------------} function rand(a, b: real): real; begin rand : = (b-a)*random + a; end; 47

Проверка точки (внутри или нет? ) {--------------------Inside – определяет, находится ли точка внутри фигуры Вход: x, y – координаты точки Выход: True, если точка внутри фигуры, False, если точка вне фигуры ---------------------} function Inside(x, y: real): Boolean; begin if (FDown(x) <= y) and (y <= FUp(x)) then Inside : = True else Inside : = False; end; function Inside(x, y: real): Boolean; begin Inside : = (FDown(x) <= y) and (y <= FUp(x)); end; 48

Метод Монте-Карло (реализация) {--------------------------Area 2 – вычисление площади методом Монте-Карло ---------------------------} procedure Area 2; var i, N, M: integer; границы x 1, x 2, y 1, y 2, x, y, S: real; прямоугольника begin (у каждого свои!) N : = 200000; M : = 0; y 2 x 1 : = xc 1; x 2 : = xc 2; y 1 : = 1; y 2 : = 4; y 1 for i: =1 to N do begin x 2 x 1 x : = rand ( x 1, x 2 ); y : = rand ( y 1, y 2 ); если на фигуре, if Inside(x, y) then M : = M + 1; увеличить счетчик end; S : = (x 2 -x 1)*(y 2 -y 1)*M/N; Moveto(250, 340); write('S = ', S: 0: 2); end; вычисление площади 49

50 Структурное программирование на языке Паскаль Тема 7. Оформление отчета © К. Ю. Поляков, 2007 -2009

Титульный лист 51

52 Графики функций через Редактор формул (Вставка – Объект – Microsoft Equation) «скриншот» (screenshot) – «снимок» экрана

Как получить копию экрана? 53 1. Поменять цвета так, чтобы все линии и текст были белые. 2. Запустить программу (она должна все нарисовать). 3. Нажать клавишу Prt. Scr (Print Screen – «снимок» экрана) на клавиатуре или комбинацию Alt+Prt. Scr ( «снимок» активного окна). 4. В графическом редакторе (Paint): Правка – Вставить. 5. Выделить нужную часть рисунка. 6. Вставить в отчет через буфер обмена (Ctrl+C, Ctrl+V).

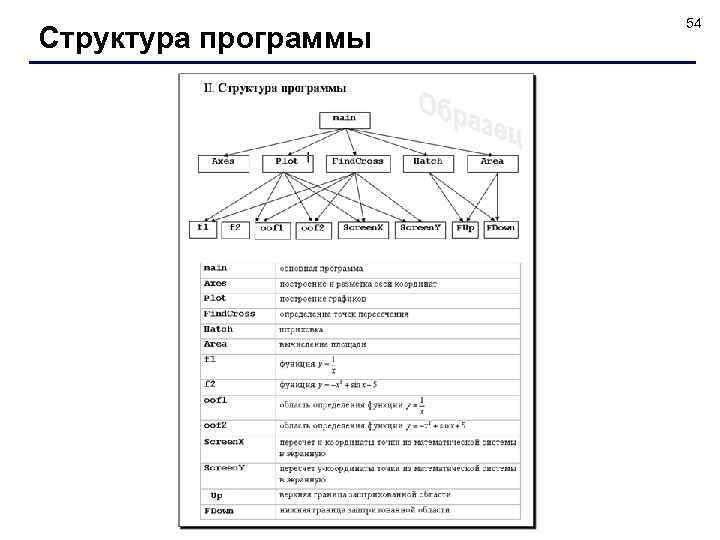Структура программы 54

55 Текст программы шрифт Courier New, (моноширинный) размер 10 пт

Конец фильма 56