1 st and 2 nd Generation Synthesis

1 st and 2 nd Generation Synthesis • Speech Synthesis Generation – First: Ground Up Synthesis – Second: Data Driven Synthesis by Concatenation • Input (Sequence of) – – Phonetic symbols Duration F 0 contours Amplification factors • Data – Rule-based parameters – Linear Prediction: Stored diphone parameters

Early Synthesis History • Klatt, 1987 – “Review of text-to-sppech conversion for English – http: //americanhistory. si. edu/archives/speechsynthesis/dk_737 b. htm – Audio: http: //www. cs. indiana. edu/rhythmsp/ASA/Contents. html • Milestones 1939 Worlds Fair, Voder, Dudley First TTS, Umeda, 1968 Low rate resynthesis, Speak and Spell, Wiggins, 1980 Natural sounding resynthesis, multi-pulse Linear Prediction, Atal, 1982 resynthesis – Natural Sounding Synthesis, Klatt, 1986 – –

Formant Synthesizer Design • Concept – Create individual components for each synthesizer unit – Feed the system with a set of parameters • Advantage – If the parameters are set properly, perfect natural sounding speech is created • Disadvantages – The combination of parameters becomes obscure – Parameter settings do not enable an automated algorithm Demo Program: http: //www. asel. udel. edu/speech/tutorials/synthesis/

Formant Synthesizer Design for individual formant Components • • IIR filter: hn = b 0 sn – a 1 yn-1 – a 2 yn-2 Transfer Function: H(z) = b 0 z 0/{(1 -a 1 z-1 – a 2 z-2)} Transfer Function: H(z) = 1/{(1 -p 1 z-1)(1 -p 2 z-1)} Because they are conjugate pairs H(z) = 1/{(1 -reiθz-1)(1 -re-iθ z-1)} = 1/(1 -re-iθ z-1 -reiθ z-1 + reiθz-1 re-i θz-1) = 1/(1 -r(e-iθ+eiθ)z-1+r 2 z-2) = 1/(1 -2 rcosθz-1+r 2 z-2) • The filter: yn = xn – 2 rcosθ yn-1+r 2 yn-2 • Parameters (θ controls formant frequency; r controls bandwidth) – Θ = 2 πf/F , r = e-πβ/F – β = desired bandwidth, F = sampling rate, f = frequency

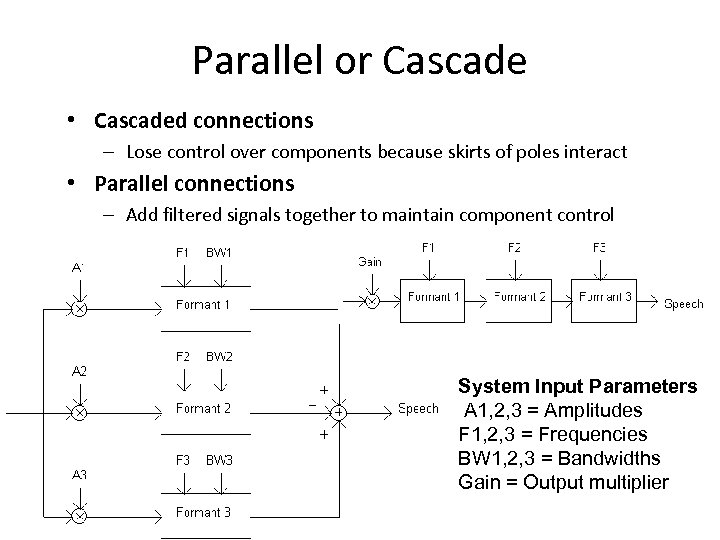Parallel or Cascade • Cascaded connections – Lose control over components because skirts of poles interact • Parallel connections – Add filtered signals together to maintain component control System Input Parameters A 1, 2, 3 = Amplitudes F 1, 2, 3 = Frequencies BW 1, 2, 3 = Bandwidths Gain = Output multiplier

Periodic Source Glottis approximation formulas • Flanagan model – Explicit periodic function u[n] = ½(1 -cos(πn/L)) if 0≤n ≤L u[n] = cos(π(n-L)/(2 M)) if L

Radiation From the Lips • Actual modeling of the lips is very complicated • Rule based synthesizers want to use specific formulas for simulation • Experiments show – Lip radiation contains at least one anti-resonance (a zero in the transfer function) – The approximation formula often used: R(z) = 1 – αz-1 where 0. 95 ≤α ≤ 0. 98 – This turns out to be the same formula for preemphasis

Consonants and Nasals • Nasals – – One resonator models the oral cavity Another resonator models the nasal cavity Add a zero in series with resonators Outputs added to generate output • Fricatives – Source either noise or glottis or both – One set of resonators model point in front of place of constriction – Another set behind point of constriction – Outputs added together

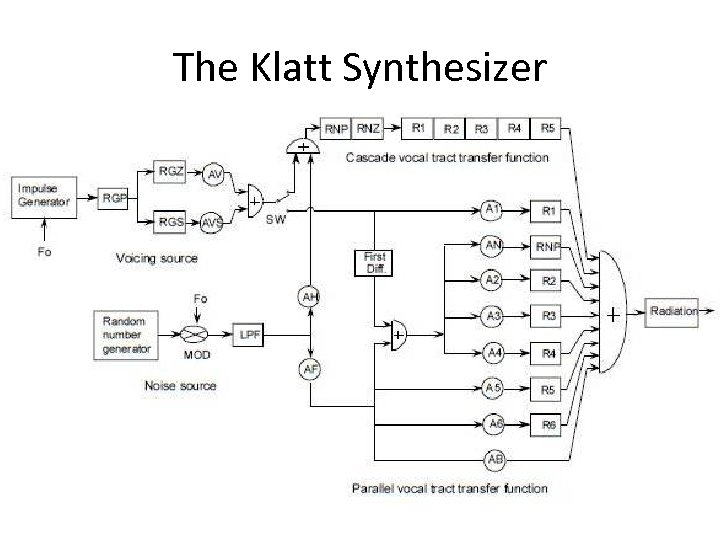The Klatt Synthesizer

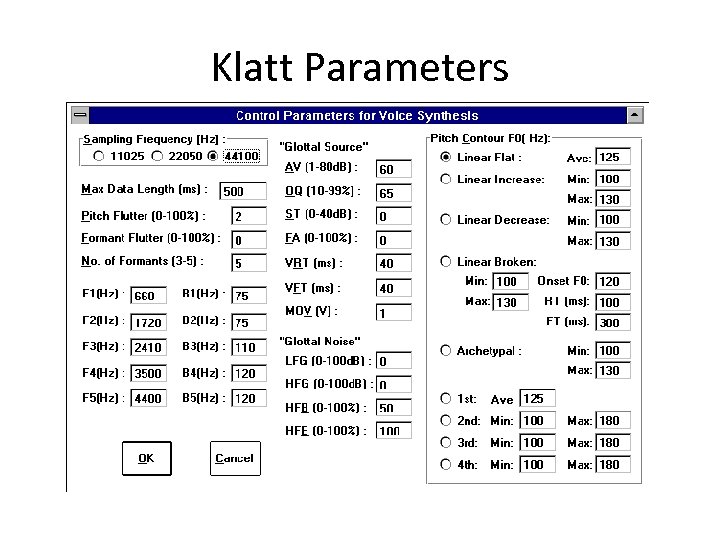Klatt Parameters

Evaluation of Formant Synthesizers • Quality – Speech produced is understandable – Output sounds metallic (not natural) • Problems – System uses lumped parameters (like components of a spring), it is not distributed (like the vocal tract) – Individually valid assumptions are invalid when joined together in a system – Speech subtleties are too complex for the formant model – Transitions between sounds is not modeled – Formants are not present in obstruent sounds

Classical Linear Prediction (LP Synthesis) • Concept – Use the all-pole tube model of Linear Prediction – Y(z) = X(z)/(1 -a 1 z-1 – a 2 z-2 - … - zpz-P) leads to the linear prediction formula yn = xn + a 1 yn-1 + a 2 yn-2 + … + apyn-p • Improvements over formant synthesis – Obtain parameters directly from speech, not from experimentation or human intervention – The glottal filter is subsumed in the LP equation, so synthesizing the glottal source becomes unnecessary • Tradeoffs – Lose modularity and physical interpretations of coefficients – Lack of zeros make modeling nasals and fricatives difficult

LP diphone-concatenation Synthesis • Definition: The unit that starts from the middle of one phone and ends at the middle of the next phone • Concept – – Capture and store the vocal tract dynamics of each frame Alter the F 0 by changing the impulse rate Alter duration as needed Concatenate stored frames together to accomplish synthesis • Input: array of {phone symbol, F 0 value, duration}

LP difficulties • Boundary point transition artifacts – Approach: Interpolate the LP parameters between adjacent frames – The output has a metallic or buzz quality because the LP filter does not entirely capture the characteristic of the source. The residual contains spikes at each pitch period • Experiment to resynthesize a speech waveform – Resynthesize with residual: speech sound perfect – Resynthesize without residual • Same pitch and duration: sounds degraded but okay • Alter pitch: speech becomes buzzy • Alter duration: degraded but okay

Articulatory Synthesis The oldest approach: mimic the vocal tract components • Kempelen – Mechanical device with tubes, bellows, and pipes – Played as one plays a musical instrument • Digital version – Controls are the tubes, not the formants – Can obtain LP tube parameters from the LP filter • Difficulties – Difficult to obtain values that shape the tubes – The glottis and lip radiation still need to be modeled – Existing models produce poor speech • Current Applicable Research – Articulatory physiology, gestures, audio-visual synthesis, talking heads

2 nd Generation Synthesis by Concatenation Extension of 1 st Generation LP-Concatenation • Comparisons to 1 st generation models – Input • Still explicitly defines the F 0 contour and duration and phonetic symbols – Output • Source waveform generated from a database of diphones (one diphone per phone) • Discards impulses and noise generators – Concatenation • Pitch and duration algorithms glue together diphones

Diphone Inventory • Requirements – If 40 phonemes • 40 left diphones and 40 right diphones can combine in 1600 ways • A phonotactic grammar can reduce the database size – Pick long units rather than short ones (It is easier to shorten duration than lengthen it) – Normalize the phases of the diphones – All diphones should have equal pitch • Finding diphone sound waves to build the inventory – Search a corpus (if one exists) – Specifically record words containing the diphones – Record nonsense words (logotomes) with desired features

Pitch-synchronous overlap and add (PSOLA) Purpose: Modify pitch or timing of a signal • PSOLA is a time domain algorithm • Pseudo code – Find the exact pitch periods in a speech signal – Create overlapping frames centered on epochs extending back and forward one pitch period – Apply hamming window – Add waves back • Closer together for higher pitch, further apart for lower pitch • Remove frames to shorten or insert frames to lengthen • Undetectable if epochs are accurately found. Why? – We are not altering the vocal filter, but changing the amplitude and spacing of the input

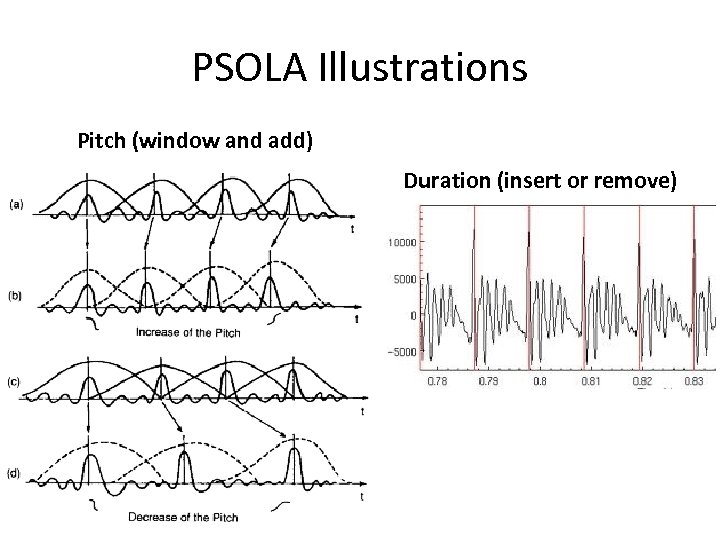PSOLA Illustrations Pitch (window and add) Duration (insert or remove)

PSOLA Epochs • PSOLA requires an exact marking of pitch points in a time domain signal • Pitch mark – Marking any part within a pitch period is okay as long as the algorithm marks the same point for every frame – The most common marking point is the instant of glottal closure, which identifies a quick time domain descent • Create an array of sample numbers comprise an analysis epoch sequence P = {p 1, p 2, …, pn} • Estimate pitch period distance = (pk – pk+1)/2

PSOLA pseudo code Identify the epochs using an array of sample indices, P For each input object Extract the desired F 0, phoneme, and duration speech = looked up phoneme sound wave from stored data Identify the epochs in the phoneme with array, P Break up the phoneme into frames If F 0 value differs from that of the phoneme Window each frame into an array of frames speech = overlap and add frames using desired F 0 IF duration is larger than desired Delete extra frames from speech at regular intervals ELSE if duration is smaller than desired Duplicate frames at regular intervals in speech Note: Multiple F 0 points in a phoneme requires multiple input objects

PSOLA Evaluation • Advantages – As a time domain algorithm, it is unlikely that any other approach is more efficient (O(N)) – If pitch and timing differences are within 25%, listeners cannot detect the alterations • Disadvantages – Epoch marking must be exact – Only pitch and timing changes are possible – If used with unit selection, several hundred megabytes of storage could be needed

LP - PSOLA • Algorithm – If the synthesizer uses linear prediction to compress phoneme sound waves, the residual portion of the signal is already available for additional waveform modifications • Algorithm – Mark the epoch points of the LP residual and overlap /combine with the PSOLA approach • Analysis – Resulting speech is competitive with PSOLA, but not superior

Sinusoidal Models Find contributing sinusoids in a signal using linear regression techniques • Definition: Statistically estimate relationships between variables that are related in a linear fashion • Advantage: The algorithm is less sensitive to finding exact pitch points • General approach 1. Filter the noise component from the signal 2. Successively match signal against a high frequency sinusoidal wave, subtracting the match from the wave 3. The lowest remaining wave is F 0 4. Use PSOLA type algorithm to alter pitch and duration

MBROLA • Overview – PSOLA synthesis has very poor quality (very hoarse quality) if the pitch points are not correctly marked. – MBROLA addresses this issue by preprocessing the database of phonemes • Ensure that all phonemes have the same phase • Force all phonemes to have the same pitch • Overlap and synthesis then works with complete accuracy Home Page: http: //tcts. fpms. ac. be/synthesis/mbrola/

Issues and Discussion • Concatenation Synthesis – Micro-concatenation Problems: • Joining phonemes can cause clicks at the boundary – Solution: Tapering waveforms at the edges • Joining segments with mismatched phases – Solution: force all segments to be phase aligned • Optimal coupling points – Solution: algorithms for matching trajectories – Solution: interpolate LP parameters – Macro-concatenation: ensure a natural spectral envelope • Requires an accurate F 0 contour