1 ші дәріс Кіріспе Әртүрлі

1 – ші дәріс

Кіріспе • Әртүрлі жәй және күрделі машиналарды, олардың бөлшектерін, күрделі құрылыстарды, үйлерді жобалау жұмыстары, әдетте, олардың кескіндерін жазықтық бетіне көрсетуден басталады. Бұңдай кескіндерді сызба деп атайды. • Қазіргі кезде адам өмірінде сызба қолданылмайтың саланы атау қиын.

• Кейбір жағдайда сызба арқылы берілетін ақпаратты басқаша түрде беру мүмкін болмайды (құрылыс, сәулет, техника). • Сызба геометрия – геометрияның бір тарауы ретінде заттардың формаларың, өзара байланысың, олардың геометриялық заңдылығын сызба арқылы зерттейді.

• Геометрияның басқа бөлімдерінде сызба тек көмекші құрал ретінде қолданылса, сызба геометрияда ол геометриялық бейнелердің қасиеттерін зерттеуде тікелей негізгі құжат ретінде қарастырылады.

Материалды баяндауда қолданылған белгілер: • кеністіктегі нүкте – латын бас әрпімен: A, B, C, …. не санмен 1, 2, 3, . . . ; • түзу не қисық сызықтар – латын кіші әрпімен: a, b, c, . . . ; • жазықтық не бет- грек кіші әрпімен: α, β, γ. . . ; • бұрыш- грек кіші әрпімен: φ , ω , β. . . ;

• проекциялар жазықтықтары – грек кіші әрпімен: • 1) фронталь проекциялар жазықтығы- π ; • 2) горизонталь проекциялар жазықтығы- π • 3) профиль проекциялар жазықтығы – π • Проекциялау бағытын анықтайтын түзу – латын кіші әрпімен: s; 1 3 2

• • • нүктенің проекциялары: фронталь проекциялары - A , B , C , . . . горизонталь проекциялары – A , B , C , . . . профиль проекциялары – A , B , C , . . . түзу не қисық сызықтардың проекциялары: фронталь проекциялары-a , b , c , . . . • горизонталь проекциялары – a , b , c , . . . • профиль проекциялары – a , b , c , . . . 1 1 1 2 3 3 2 2 3 2

Негізгі операциялар • - тік бұрыш; • - екі геометриялық элементтің сәйкестілігі; • - екі геометриялық элементтің қиылысуы; • - екі геометриялық элементтің айқасуы; • - екі геометриялық элеметтің тиістілігі; • - логикалық салдар; • / - теріс ұғым; • - бұрыш нәтижесі;

Проекция әдісі • Кескіндерді салу үшін жазықтыққа проекциялау әдісі қолданылады.

Центрлік проекция • Егер барлық проекциялаушы түзулер тек бір нүкте арқылы өтсе, онда проекция центрлік проекция деп аталады -1 -ші сурет

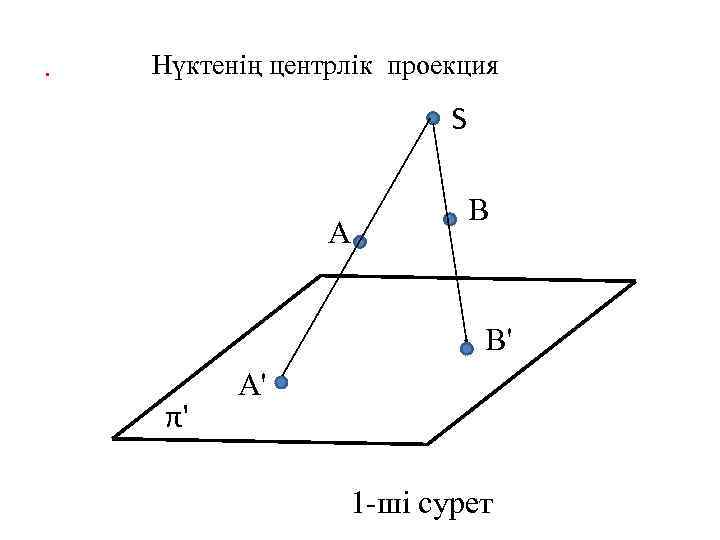. Нүктенің центрлік проекция S A B B' π' A' 1 -ші сурет

Центрлік проекция (1 -ші сурет) S – проекциялар центрі; π' - проекциялар жазықтығы; А, В – берілген нүктелер; SA ; SB – проекциялаушы сәулелер A' = SA π‘; В'=SB π' А' – А нүктенің центрлік проекциясы; В'- В нүктенің центрлік проекциясы

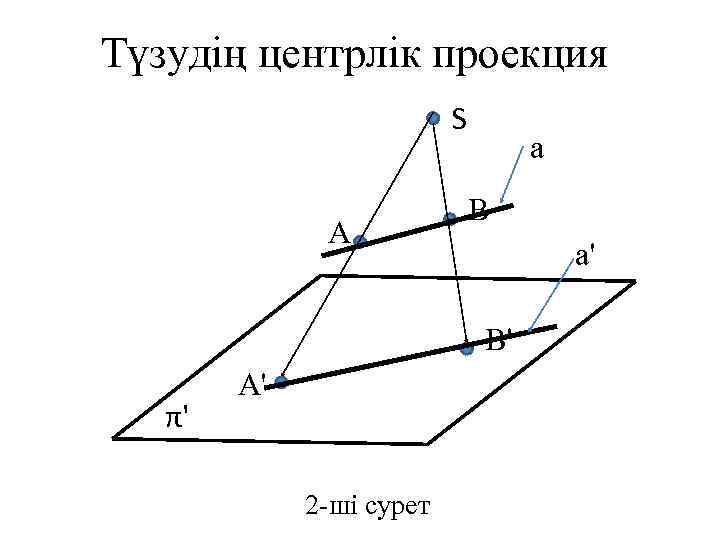Түзудің центрлік проекция S A a B a' B' π' A' 2 -ші сурет

Центрлік проекция (2 -ші сурет) а түзу A және В нүктелер арқылы өтеді; а түзу А' және В нүктелер арқылы өтеді; а'- а түзудің центрлік проекциясы

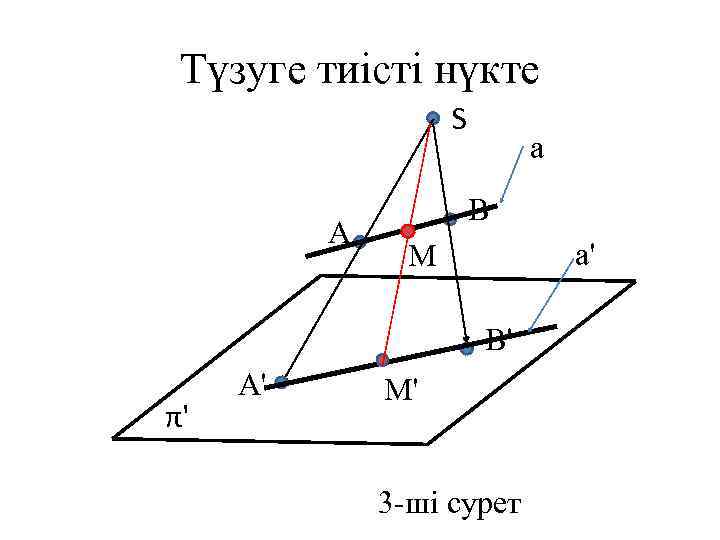Түзуге тиісті нүкте S A a B a' M B' π' A' M' 3 -ші сурет

Түзуге тиісті нүкте (3 -ші сурет) Берілген М' нүкте, тиісті а түзуіне; М нүктені табу керек SМ' кері проекциялау сәулені тұрғызу керек; М нүктесі SМ' сәуленің а түзуімен қиылысуынан пайда болады.

Параллель проекция - егер проекциялауші сәулелер өзара параллель болса, онда проекция параллель проекция деп аталады.

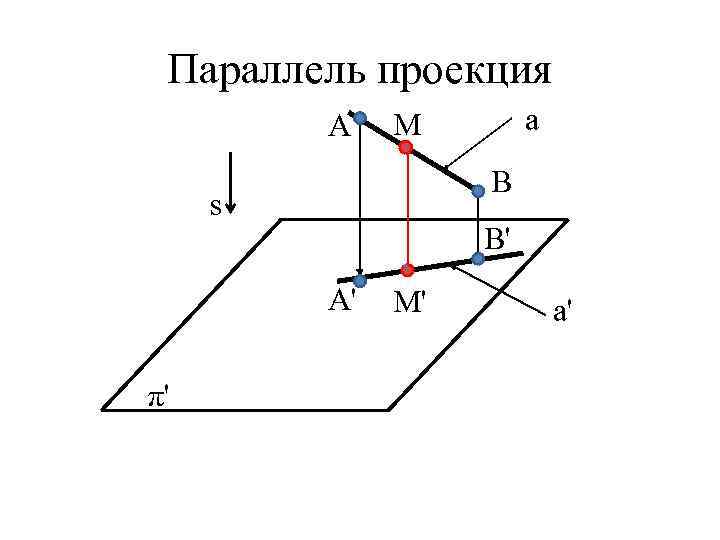Параллель проекция A B s B' A' π' a М М' a'

Параллель проекциялаудың қасіеттері: 1. Түзудің проекциясы түзу болады 2. Нүктенің проекциясы нүкте болады 3. Проекциялаушы түзуге параллель орналасқан түзудін проекциясы нүкте болады. 4. Түзуге тиісті нүктенің проекциясы, сол түзудің проекциясында жатады. 5. Егер екі түзу өзара параллель болса, онда олардың проекциялары да параллель болады.