Скачать презентацию 1 Section 1 4 Formulas for Linear Скачать презентацию 1 Section 1 4 Formulas for Linear

060f9f21f098358ba3c085535ef53a75.ppt

  • Количество слайдов: 63

1 1

Section 1. 4 Formulas for Linear Functions 2 Section 1. 4 Formulas for Linear Functions 2

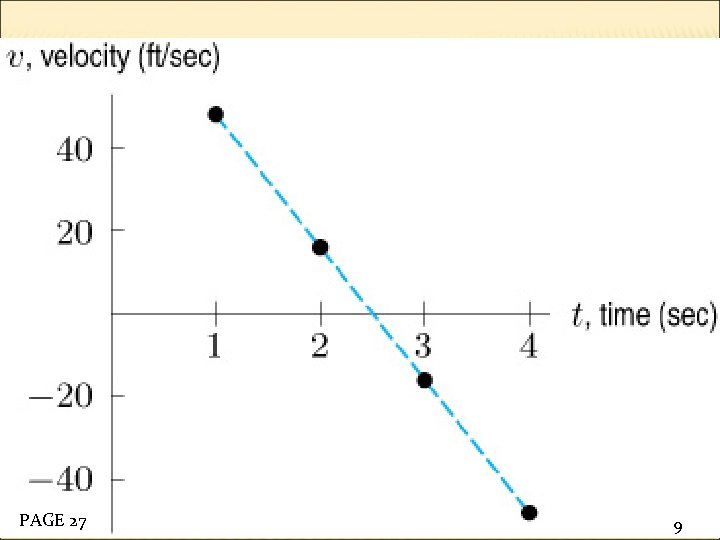
A grapefruit is thrown into the air. Its velocity, v, is a linear function A grapefruit is thrown into the air. Its velocity, v, is a linear function of t, the time since it was thrown. (A positive velocity indicates the grapefruit is rising and a negative velocity indicates it is falling. ) Check that the data in Table 1. 30 corresponds to a linear function. Find a formula for v in terms of t. PAGE 27 EXAMPLE 1 3

A grapefruit is thrown into the air. Its velocity, v, is a linear function A grapefruit is thrown into the air. Its velocity, v, is a linear function of t, the time since it was thrown. (A positive velocity indicates the grapefruit is rising and a negative velocity indicates it is falling. ) Check that the data in Table 1. 30 corresponds to a linear function. Find a formula for v in terms of t. We will calculate: Rate of change of velocity with respect to time (or rate of change, for short). PAGE 27 4

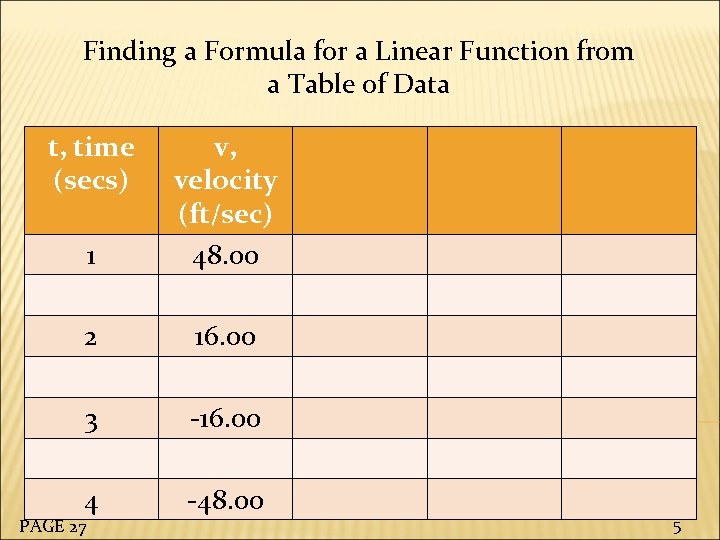Finding a Formula for a Linear Function from a Table of Data t, time Finding a Formula for a Linear Function from a Table of Data t, time (secs) 1 v, velocity (ft/sec) 48. 00 2 16. 00 3 -16. 00 4 -48. 00 PAGE 27 5

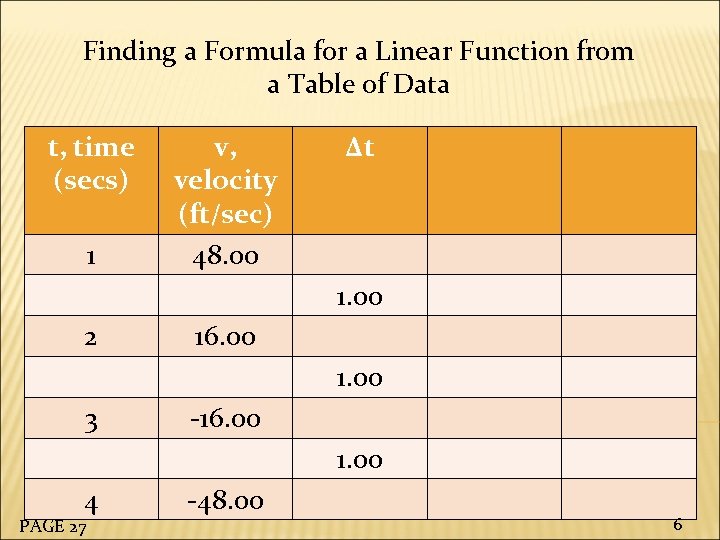Finding a Formula for a Linear Function from a Table of Data t, time Finding a Formula for a Linear Function from a Table of Data t, time (secs) 1 v, velocity (ft/sec) 48. 00 Δt 1. 00 2 16. 00 1. 00 3 -16. 00 1. 00 4 PAGE 27 -48. 00 6

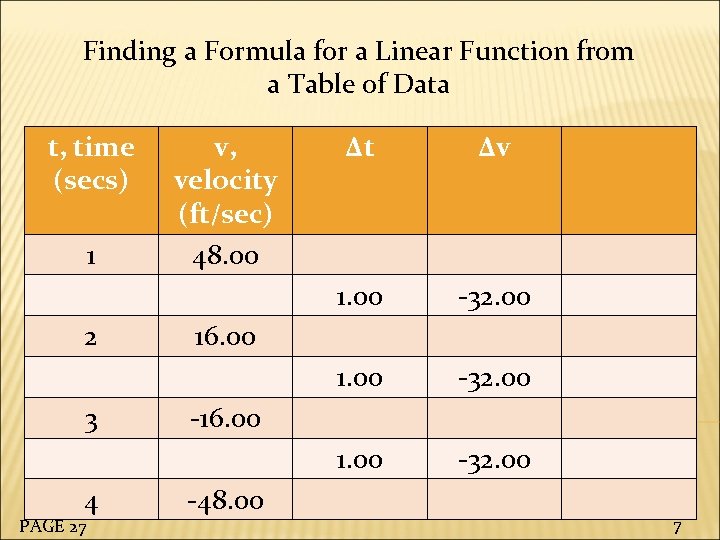Finding a Formula for a Linear Function from a Table of Data t, time Finding a Formula for a Linear Function from a Table of Data t, time (secs) 4 PAGE 27 -32. 00 1. 00 3 Δv 1. 00 2 Δt 1. 00 1 v, velocity (ft/sec) 48. 00 -32. 00 16. 00 -48. 00 7

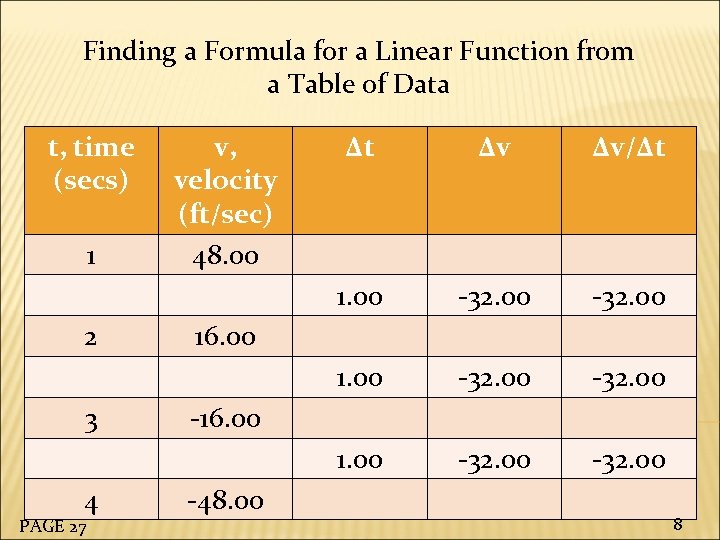Finding a Formula for a Linear Function from a Table of Data t, time Finding a Formula for a Linear Function from a Table of Data t, time (secs) 4 PAGE 27 Δv/Δt -32. 00 1. 00 3 Δv 1. 00 2 Δt 1. 00 1 v, velocity (ft/sec) 48. 00 -32. 00 16. 00 -48. 00 8

PAGE 27 9 PAGE 27 9

Since v is a function of t, we have: v = f(t). We also Since v is a function of t, we have: v = f(t). We also remember from Section 1. 3: m = ? PAGE 28 10

Since v is a function of t, we have: v = f(t). We also Since v is a function of t, we have: v = f(t). We also remember from Section 1. 3: m = slope (or the rate of change = Δv/Δt) Here, m = ? PAGE 28 11

Since v is a function of t, we have: v = f(t). We also Since v is a function of t, we have: v = f(t). We also remember from Section 1. 3: m = slope (or the rate of change = Δv/Δt) Here, m = -32. So we have: v = b + mt or v = b -32 t PAGE 28 12

v = b -32 t How do we solve for b? PAGE 28 13 v = b -32 t How do we solve for b? PAGE 28 13

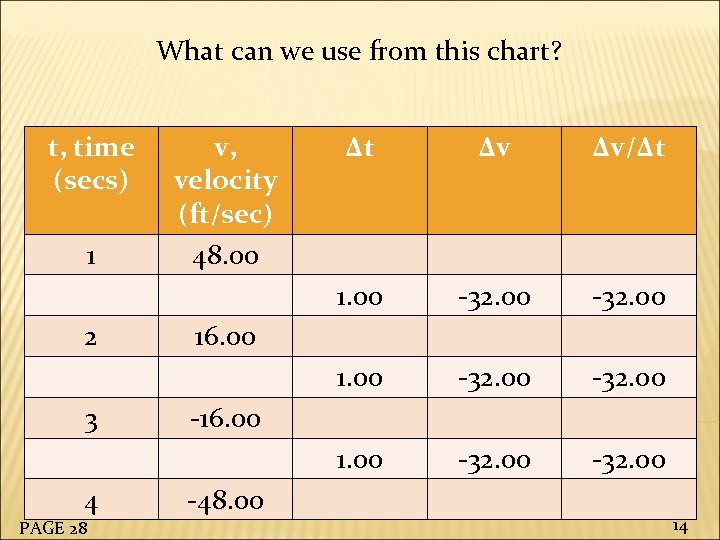What can we use from this chart? t, time (secs) 4 PAGE 28 Δv/Δt What can we use from this chart? t, time (secs) 4 PAGE 28 Δv/Δt -32. 00 1. 00 3 Δv 1. 00 2 Δt 1. 00 1 v, velocity (ft/sec) 48. 00 -32. 00 16. 00 -48. 00 14

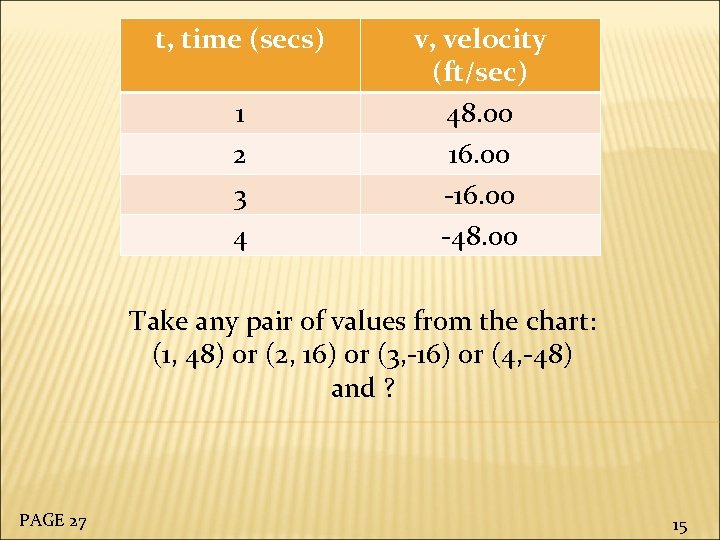t, time (secs) 1 2 3 4 v, velocity (ft/sec) 48. 00 16. 00 t, time (secs) 1 2 3 4 v, velocity (ft/sec) 48. 00 16. 00 -48. 00 Take any pair of values from the chart: (1, 48) or (2, 16) or (3, -16) or (4, -48) and ? PAGE 27 15

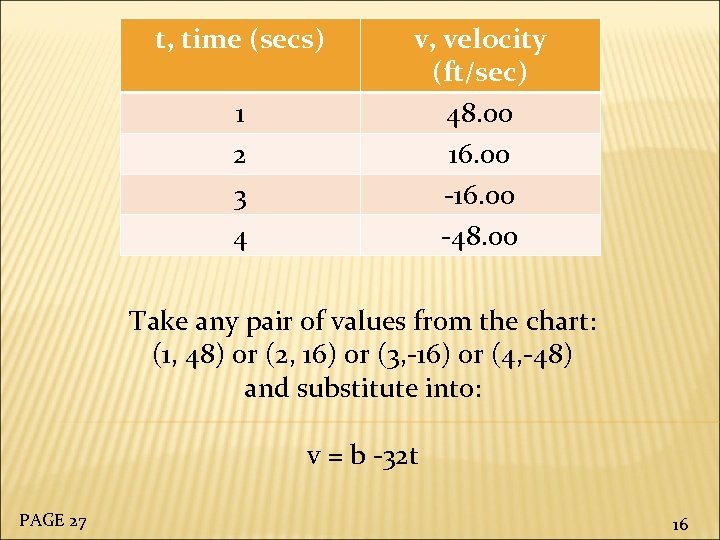t, time (secs) 1 2 3 4 v, velocity (ft/sec) 48. 00 16. 00 t, time (secs) 1 2 3 4 v, velocity (ft/sec) 48. 00 16. 00 -48. 00 Take any pair of values from the chart: (1, 48) or (2, 16) or (3, -16) or (4, -48) and substitute into: v = b -32 t PAGE 27 16

Take any pair of values from the chart: (1, 48) or (2, 16) or Take any pair of values from the chart: (1, 48) or (2, 16) or (3, -16) or (4, -48) and substitute into: v = b -32 t (1, 48): 48 = b - 32(1) → 48 + 32 = b → b = 80 PAGE 27 17

Take any pair of values from the chart: (1, 48) or (2, 16) or Take any pair of values from the chart: (1, 48) or (2, 16) or (3, -16) or (4, -32) and substitute into: v = b -32 t (1, 48): 48 = b - 32(1) → 48 + 32 = b → b = 80 (2, 16): 16 = b - 32(2) → 16 + 64 = b → b = 80 PAGE 27 18

Take any pair of values from the chart: (1, 48) or (2, 16) or Take any pair of values from the chart: (1, 48) or (2, 16) or (3, -16) or (4, -32) and substitute into: v = b -32 t (1, 48): 48 = b - 32(1) → 48 + 32 = b → b = 80 (2, 16): 16 = b - 32(2) → 16 + 64 = b → b = 80 (3, -16): -16 = b - 32(3) → -16 + 96 = b → b = 80 PAGE 27 19

Take any pair of values from the chart: (1, 48) or (2, 16) or Take any pair of values from the chart: (1, 48) or (2, 16) or (3, -16) or (4, -32) and substitute into: v = b -32 t (1, 48): 48 = b - 32(1) → 48 + 32 = b → b = 80 (2, 16): 16 = b - 32(2) → 16 + 64 = b → b = 80 (3, -16): -16 = b - 32(3) → -16 + 96 = b → b = 80 (4, -48): -48 = b -32(4) → -48 + 128 = b → b = 80 PAGE 27 20

So what is our final equation? PAGE 28 21 So what is our final equation? PAGE 28 21

So what is our final equation? v = 80 - 32 t PAGE 28 So what is our final equation? v = 80 - 32 t PAGE 28 22

v = 80 - 32 t Note: m = -32 ft/sec per second (a. v = 80 - 32 t Note: m = -32 ft/sec per second (a. k. a. ft/sec 2) implies: the grapefruit’s velocity is decreasing by 32 ft/sec for every second that goes by. “The grapefruit is accelerating at -32 ft/sec per second. ” Negative acceleration is also called deceleration. (Note: no shorthand way of saying “ft/sec per second”. ) PAGE 28 23

Finding a Formula for a Linear Function from a Graph We can calculate the Finding a Formula for a Linear Function from a Graph We can calculate the slope, m, of a linear function using two points on its graph. Having found m, we can use either of the points to calculate b, the vertical intercept. PAGE 28 24

Figure 1. 25 shows oxygen consumption as a function of heart rate for two Figure 1. 25 shows oxygen consumption as a function of heart rate for two people. (a) Assuming linearity, find formulas for these two functions. (b) Interpret the slope of each graph in terms of oxygen consumption. PAGE 28 EXAMPLE 2 25

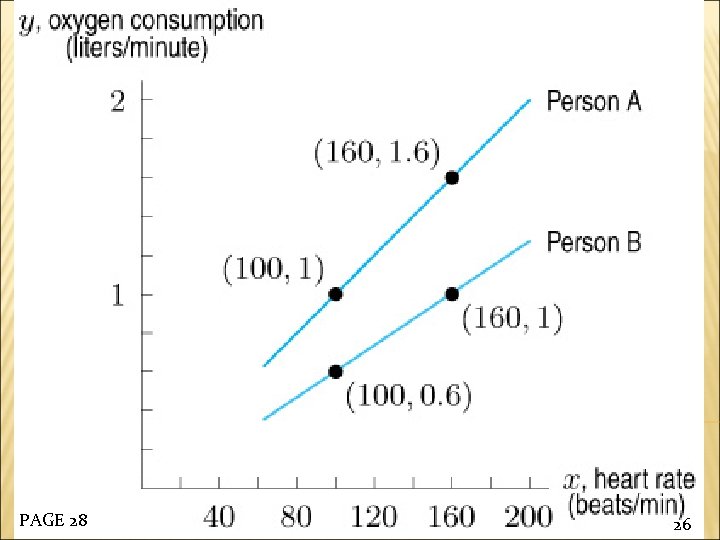PAGE 28 26 PAGE 28 26

Let's calculate m: PAGE 29 27 Let's calculate m: PAGE 29 27

Let's calculate m: PAGE 29 28 Let's calculate m: PAGE 29 28

Let's calculate m: PAGE 29 29 Let's calculate m: PAGE 29 29

What are our 2 linear equations so far? PAGE 29 30 What are our 2 linear equations so far? PAGE 29 30

What are our 2 linear equations so far? For person A: PAGE 29 31 What are our 2 linear equations so far? For person A: PAGE 29 31

What are our 2 linear equations so far? For person A: For person B: What are our 2 linear equations so far? For person A: For person B: PAGE 29 32

Now let's calculate b: PAGE 29 33 Now let's calculate b: PAGE 29 33

Now let's calculate b: PAGE 29 34 Now let's calculate b: PAGE 29 34

Now let's calculate b: PAGE 29 35 Now let's calculate b: PAGE 29 35

What are our 2 linear equations? PAGE 29 36 What are our 2 linear equations? PAGE 29 36

What are our 2 linear equations? For person A: PAGE 29 37 What are our 2 linear equations? For person A: PAGE 29 37

What are our 2 linear equations? For person A: For person B: PAGE 29 What are our 2 linear equations? For person A: For person B: PAGE 29 38

Figure 1. 25 shows oxygen consumption as a function of heart rate for two Figure 1. 25 shows oxygen consumption as a function of heart rate for two people. (b) Interpret the slope of each graph in terms of oxygen consumption. What about (b)? PAGE 29 39

Here are two remindersthis slide and the next: PAGE 29 40 Here are two remindersthis slide and the next: PAGE 29 40

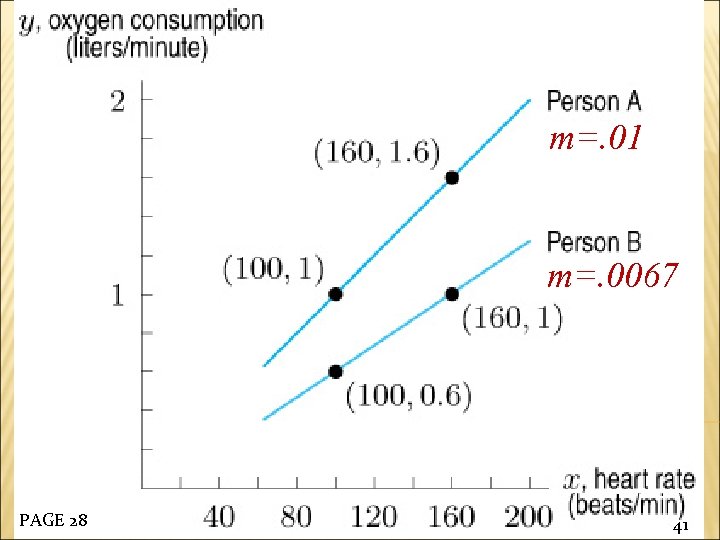m=. 01 m=. 0067 PAGE 28 41 m=. 01 m=. 0067 PAGE 28 41

Since the slope for person B is smaller than for person A, person B Since the slope for person B is smaller than for person A, person B consumes less additional oxygen than person A. PAGE 29 42

We have $24 to spend on soda and chips for a party. A six-pack We have $24 to spend on soda and chips for a party. A six-pack of soda costs $3 and a bag of chips costs $2. The number of six-packs we can afford, y, is a function of the number of bags of chips we decide to buy, x. (a) Find an equation relating x and y. (b) Graph the equation. Interpret the intercepts and the slope in the context of the party. PAGE 30 EXAMPLE 3 43

Let: x = # of bags of chips y = # of six-packs Let: x = # of bags of chips y = # of six-packs of soda PAGE 30 44

Let: x = # of bags of chips $2 x = amount spent Let: x = # of bags of chips $2 x = amount spent on chips y = # of six-packs of soda PAGE 30 45

Let: x = # of bags of chips $2 x = amount spent Let: x = # of bags of chips $2 x = amount spent on chips y = # of six-packs of soda $3 y = amount spent on soda PAGE 30 46

Let: x = # of bags of chips $2 x = amount spent Let: x = # of bags of chips $2 x = amount spent on chips y = # of six-packs of soda $3 y = amount spent on soda & 2 x + 3 y = 24 PAGE 30 47

2 x + 3 y = 24 Let's solve for y: PAGE 30 2 x + 3 y = 24 Let's solve for y: PAGE 30 48

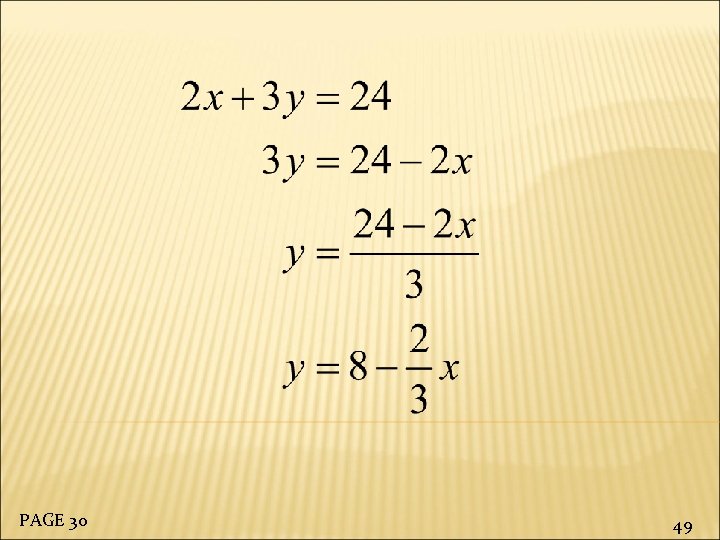PAGE 30 49 PAGE 30 49

What is the slope and what is the y intercept? PAGE 30 50 What is the slope and what is the y intercept? PAGE 30 50

What is the slope and what is the y intercept? PAGE 30 51 What is the slope and what is the y intercept? PAGE 30 51

(b) Graph the equation. Interpret the intercepts and the slope in the context of (b) Graph the equation. Interpret the intercepts and the slope in the context of the party. PAGE 30 52

x (chips) y (soda) Let's plot some points: PAGE N/A 53 x (chips) y (soda) Let's plot some points: PAGE N/A 53

x (chips) Let's plot some points: y (soda) 0 1 2 3 4 5 x (chips) Let's plot some points: y (soda) 0 1 2 3 4 5 6 7 8 9 10 11 PAGE N/A 12 54

x (chips) 8. 0000 1 7. 3333 6. 6667 3 6. 0000 4 5. x (chips) 8. 0000 1 7. 3333 6. 6667 3 6. 0000 4 5. 3333 5 4. 6667 6 4. 0000 7 3. 3333 8 2. 6667 9 2. 0000 10 1. 3333 11 PAGE N/A 0 2 Let's plot some points: y (soda) 0. 6667 12 0. 0000 55

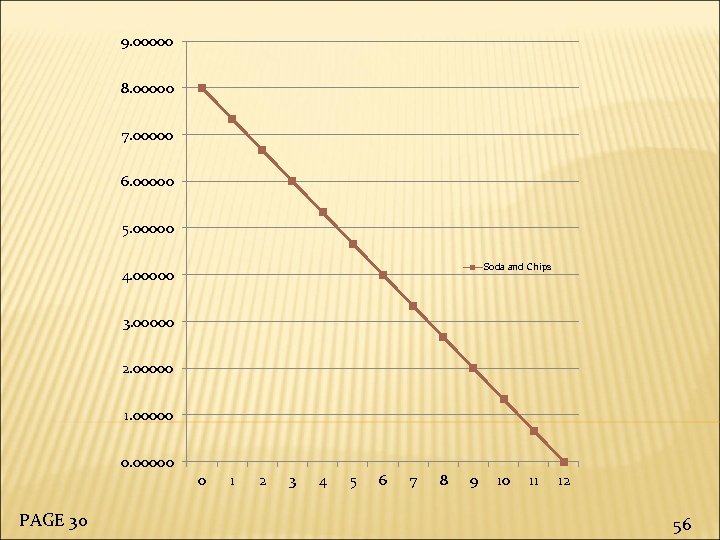9. 00000 8. 00000 7. 00000 6. 00000 5. 00000 Soda and Chips 4. 9. 00000 8. 00000 7. 00000 6. 00000 5. 00000 Soda and Chips 4. 00000 3. 00000 2. 00000 1. 00000 0 PAGE 30 1 2 3 4 5 6 7 8 9 10 11 12 56

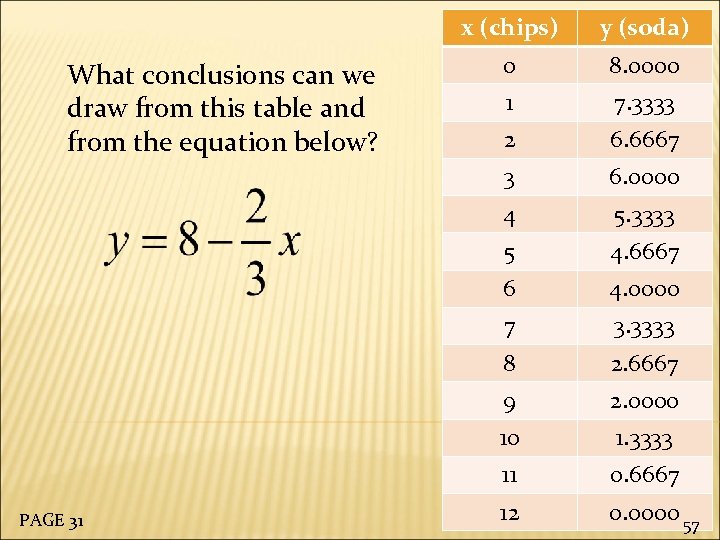x (chips) 8. 0000 1 7. 3333 2 6. 6667 6. 0000 4 5. x (chips) 8. 0000 1 7. 3333 2 6. 6667 6. 0000 4 5. 3333 5 4. 6667 6 4. 0000 7 3. 3333 8 2. 6667 9 2. 0000 10 1. 3333 11 PAGE 31 0 3 What conclusions can we draw from this table and from the equation below? y (soda) 0. 6667 12 0. 0000 57

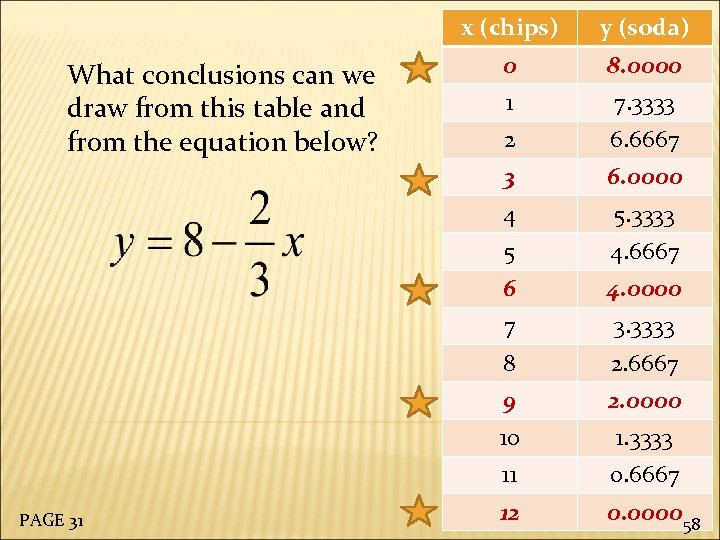x (chips) 8. 0000 1 7. 3333 2 6. 6667 6. 0000 4 5. x (chips) 8. 0000 1 7. 3333 2 6. 6667 6. 0000 4 5. 3333 5 4. 6667 6 4. 0000 7 3. 3333 8 2. 6667 9 2. 0000 10 1. 3333 11 PAGE 31 0 3 What conclusions can we draw from this table and from the equation below? y (soda) 0. 6667 12 0. 000058

x (chips) 8. 0000 1 7. 3333 2 6. 6667 6. 0000 4 5. x (chips) 8. 0000 1 7. 3333 2 6. 6667 6. 0000 4 5. 3333 5 4. 6667 6 4. 0000 7 3. 3333 8 2. 6667 9 2. 0000 10 1. 3333 11 PAGE 31 0 3 What conclusions can we draw from this table and from the equation below? y (soda) 0. 6667 12 0. 000059

x (chips) What conclusions can we draw from this table and from the equation x (chips) What conclusions can we draw from this table and from the equation below? y (soda) 0 8. 0000 1 7. 3333 2 +3 6. 6667 -2 3 4 5. 3333 5 4. 6667 6 4. 0000 7 3. 3333 8 2. 6667 9 2. 0000 10 1. 3333 11 PAGE 31 6. 0000 0. 6667 12 0. 000060

x (chips) 0 8. 0000 1 7. 3333 2 6. 6667 3 6. 0000 x (chips) 0 8. 0000 1 7. 3333 2 6. 6667 3 6. 0000 4 5. 3333 5 4. 6667 6 4. 0000 7 3. 3333 8 2. 6667 9 2. 0000 10 What conclusions can we draw from this table and from the equation below? y (soda) 1. 3333 11 -3 PAGE 31 0. 6667 +2 12 0. 0000 61

Alternative Forms for the Equation of a Line: • Slope-Intercept Form: y = b Alternative Forms for the Equation of a Line: • Slope-Intercept Form: y = b + mx [m=slope, y=y-int] • Point-Slope Form: y – yo = m(x – xo) [m=slope, (xo, yo) point on the line] • Standard Form: Ax + By + C = 0 [A, B, C constants] PAGE 31 62

End of Section 1. 4 63 End of Section 1. 4 63