3ca3fca17646fefca3fdfcb1d50c078c.ppt
- Количество слайдов: 20

(1) Schedule Mar 15 Linkage disequilibrium (LD) mapping Mar 17 LD mapping Mar 22 Guest speaker, Dr Yang Mar 24 Overview Attend ENAR Biometrical meeting in Austin from Mar 20 to 23 (2) Projects - Work on a problem learnt in the class - Select a problem from your own projects

What I have learnt from my trip to Seattle -Fred Hutchinson Cancer Research Center -University of Washington Statistical Genetics of Complex Traits Single Nucleotide Polymorphisms (SNPs) Haplotype blocks HIV/AIDS dynamics Cancer progression

Statistical Genetics of Complex Traits Linkage, Disequilibrium and QTL Rongling Wu, Chang-Xing Ma and George Casella Springer-Verlag New York

Linkage Disequilibrium • Linkage analysis – controlled crosses (backcross or F 2) and structured pedigrees (grandparent-children generation) • Linkage disequilibrium analysis – Natural population • Linkage mapping is used in plant and animal genetics, as well as human genetics of diseases like cancers. • LD mapping is used for human genetics of diseases like HIV/AIDS and SARS.

Linkage mapping - backcross Mixture model-based likelihood without marker information L(y| ) = i=1 n [½f 1(yi) + ½f 0(yi)] Sample 1 2 3 4 5 6 7 8 Height (cm, y) 184 185 180 182 167 169 165 166 QTL genotype Qq ½ ½ ½ ½ qq ½ ½ ½ ½
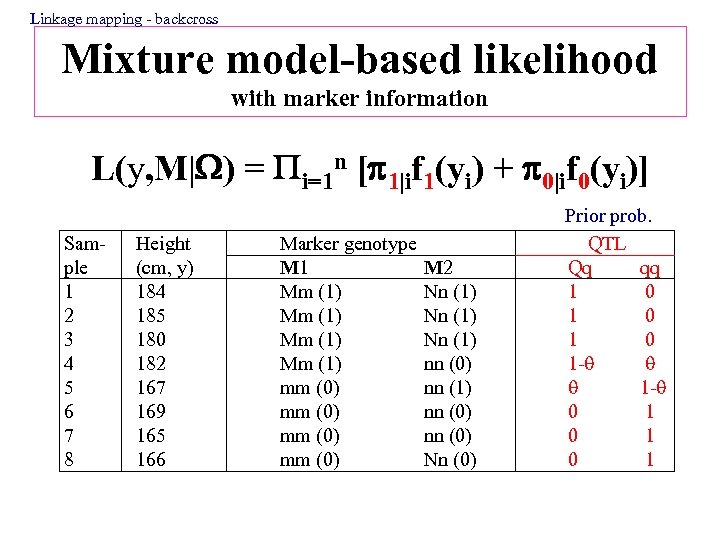
Linkage mapping - backcross Mixture model-based likelihood with marker information L(y, M| ) = i=1 n [ 1|if 1(yi) + 0|if 0(yi)] Sample 1 2 3 4 5 6 7 8 Height (cm, y) 184 185 180 182 167 169 165 166 Marker genotype M 1 Mm (1) mm (0) M 2 Nn (1) nn (0) Nn (0) Prior prob. QTL Qq qq 1 0 1 0 1 - 1 - 0 1 0 1

Linkage mapping - backcross Conditional probabilities of the QTL genotypes (missing) based on marker genotypes (observed) L(y, M| ) = i=1 n [ 1|if 1(yi) + 0|if 0(yi)] = i=1 n 1 [1 f 1(yi) i=1 n 2 [(1 - ) f 1(yi) i=1 n 3 [ f 1(yi) i=1 n 4 [0 f 1(yi) +0 f 0(yi)] + (1 - ) f 0(yi)] +1 f 0(yi)] Conditional on 11 (n 1) Conditional on 10 (n 2) Conditional on 01 (n 3) Conditional on 00 (n 4)

Linkage mapping - backcross Normal distributions of phenotypic values for each QTL genotype group f 1(yi) = 1/(2 2)1/2 exp[-(yi- 1)2/(2 2)], 1 = + a* f 0(yi) = 1/(2 2)1/2 exp[-(yi- 0)2/(2 2)], 0 =

Linkage mapping - backcross Differentiating L with respect to each unknown parameter, setting derivatives equal zero and solving the log-likelihood equations L(y, M| ) = i=1 n[ 1|if 1(yi) + 0|if 0(yi)] log L(y, M| ) = i=1 n log[ 1|if 1(yi) + 0|if 0(yi)] Define 1|i = 1|if 1(yi)/[ 1|if 1(yi) + 0|if 0(yi)] 0|i = 0|if 1(yi)/[ 1|if 1(yi) + 0|if 0(yi)] (1) (2) 1 = i=1 n( 1|iyi)/ i=1 n 1|i 0 = i=1 n( 0|iyi)/ i=1 n 0|i 2 = 1/n i=1 n[ 1|i(yi- 1)2+ 0|i(yi- 0)2] = ( i=1 n 2 1|i + i=1 n 3 0|i)/(n 2+n 3) (4) (5) (6)

Linkage disequilibrium mapping – natural population Mixture model-based likelihood without marker information Suppose there is natural population with a segregating QTL of two alternative alleles, Q and q, Prob(Q)=q, Prob(q)=1 -q → Prob(QQ)=q 2, Prob(Qq)=2 q(1 -q), Prob(qq)=(1 -q)2 L(y| ) = i=1 n [[q 2 f 2(yi) + 2 q(1 -q)f 1(yi) + (1 -q)2 f 0(yi)] Sample 1 2 3 4 5 6 7 8 Height (cm, y) 184 185 180 182 167 169 165 166 QTL genotype QQ Qq 2 q 2 q(1 -q) q 2 2 q(1 -q) 2 q 2 q(1 -q) q 2 2 q(1 -q) qq (1 -q)2 (1 -q)2

Linkage disequilibrium mapping – natural population Association between marker and QTL -Marker, Prob(M)=p, Prob(m)=1 -p -QTL, Prob(Q)=q, Prob(q)=1 -q Four haplotypes: Prob(MQ)=p 11=pq+D Prob(Mq)=p 10=p(1 -q)-D Prob(m. Q)=p 01=(1 -p)q-D Prob(mq)=p 00=(1 -p)(1 -q)+D p=(p 11+p 10)/2 q=(p 11+p 01)/2 D=p 11 p 00 -p 10 p 01
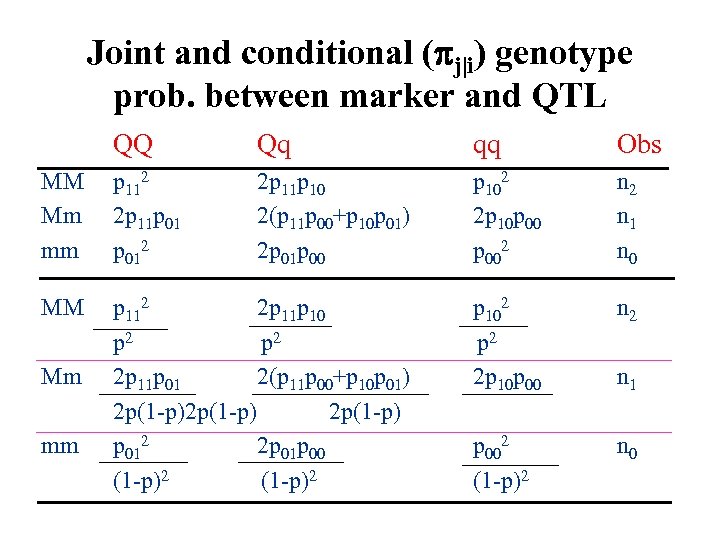
Joint and conditional ( j|i) genotype prob. between marker and QTL QQ Qq qq Obs MM Mm mm p 112 2 p 11 p 012 2 p 11 p 10 2(p 11 p 00+p 10 p 01) 2 p 01 p 00 p 102 2 p 10 p 002 n 1 n 0 MM p 112 2 p 11 p 10 p 2 2 p 11 p 01 2(p 11 p 00+p 10 p 01) 2 p(1 -p) p 012 2 p 01 p 00 (1 -p)2 p 102 p 2 2 p 10 p 00 n 2 p 002 (1 -p)2 n 0 Mm mm n 1

Linkage disequilibrium mapping – natural population Mixture model-based likelihood with marker information L(y, M| )= i=1 n[ 2|if 2(yi) + 1|if 1(yi) + 0|if 0(yi)] Prior prob. Sample 1 2 3 4 5 6 7 8 Height (cm, y) 184 185 180 182 167 169 165 166 Marker genotype M MM (2) Mm (1) mm (0) QTL genotype QQ Qq 2|i 1|i 2|i 1|i qq 0|i 0|i

Linkage disequilibrium mapping – natural population Conditional probabilities of the QTL genotypes (missing) based on marker genotypes (observed) L(y, M| ) = i=1 n [ 2|if 2(yi) + 1|if 1(yi) + 0|if 0(yi)] = i=1 n 2 [ 2|2 if 2(yi) + 1|2 if 1(yi) + 0|2 if 0(yi)] Conditional on 2 (n 2) i=1 n 1 [ 2|1 if 2(yi) + 1|1 if 1(yi) + 0|1 if 0(yi)] Conditional on 1 (n 1) i=1 n 0 [ 2|0 if 2(yi) + 1|0 if 1(yi) + 0|0 if 0(yi)] Conditional on 0 (n 0)

Linkage disequilibrium mapping – natural population Normal distributions of phenotypic values for each QTL genotype group f 2(yi) = 1/(2 2)1/2 exp[-(yi- 2)2/(2 2)], 2 = + a f 1(yi) = 1/(2 2)1/2 exp[-(yi- 1)2/(2 2)], 1 = + d f 0(yi) = 1/(2 2)1/2 exp[-(yi- 0)2/(2 2)], 0 = - a

Linkage disequilibrium mapping – natural population Differentiating L with respect to each unknown parameter, setting derivatives equal zero and solving the log-likelihood equations L(y, M| ) = i=1 n[ 2|if 2(yi) + 1|if 1(yi) + 0|if 0(yi)] log L(y, M| ) = i=1 n log[ 2|if 2(yi) + 1|if 1(yi) + 0|if 0(yi)] Define 2|i = 2|if 1(yi)/[ 2|if 2(yi) + 1|if 1(yi) + 0|if 0(yi)] 1|i = 1|if 1(yi)/[ 2|if 2(yi) + 1|if 1(yi) + 0|if 0(yi)] 0|i = 0|if 1(yi)/[ 2|if 2(yi) + 1|if 1(yi) + 0|if 0(yi)] (1) (2) (3) 1 = i=1 n( 1|iyi)/ i=1 n 1|i 0 = i=1 n( 0|iyi)/ i=1 n 0|i 2 = 1/n i=1 n[ 1|i(yi- 1)2+ 0|i(yi- 0)2] (4) (5) (6)

Complete data QQ Prior prob Qq qq Obs MM Mm mm p 112 2 p 11 p 012 2 p 11 p 10 2(p 11 p 00+p 10 p 01) 2 p 01 p 00 p 102 2 p 10 p 002 n 1 n 0 QQ Qq qq Obs n 20 n 10 n 00 n 2 n 1 n 0 MM n 22 n 21 Mm n 12 n 11 mm n 02 n 01 p 11=[2 n 22 + (n 21+n 12) + n 22]/2 n, p 10=[2 n 20 + (n 21+n 10) + (1 - )n 22]/2 n, p 01=[2 n 02 + (n 12+n 01) + (1 - )n 22]/2 n, p 11=[2 n 00 + (n 10+n 01) + n 22]/2 n, =p 11 p 00/(p 11 p 00+p 10 p 01)
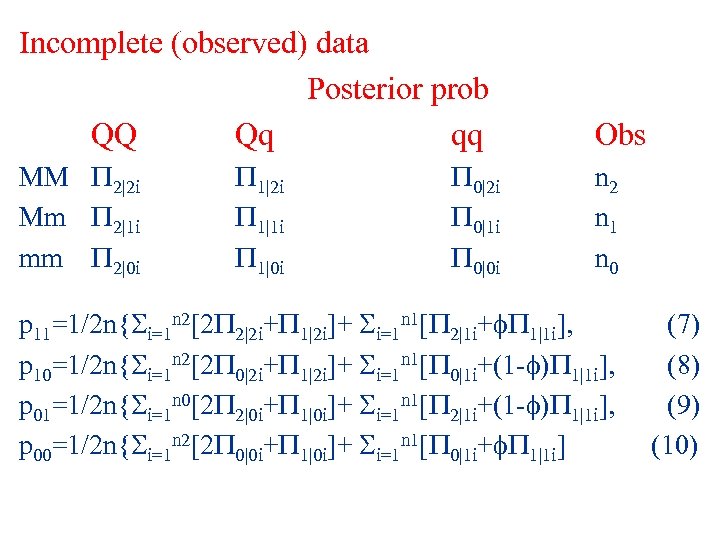
Incomplete (observed) data Posterior prob QQ Qq qq Obs MM 2|2 i Mm 2|1 i mm 2|0 i n 2 n 1 n 0 1|2 i 1|1 i 1|0 i 0|2 i 0|1 i 0|0 i p 11=1/2 n{ i=1 n 2[2 2|2 i+ 1|2 i]+ i=1 n 1[ 2|1 i+ 1|1 i], p 10=1/2 n{ i=1 n 2[2 0|2 i+ 1|2 i]+ i=1 n 1[ 0|1 i+(1 - ) 1|1 i], p 01=1/2 n{ i=1 n 0[2 2|0 i+ 1|0 i]+ i=1 n 1[ 2|1 i+(1 - ) 1|1 i], p 00=1/2 n{ i=1 n 2[2 0|0 i+ 1|0 i]+ i=1 n 1[ 0|1 i+ 1|1 i] (7) (8) (9) (10)

EM algorithm (1) Give initiate values (0) =( 2, 1, 0, 2, p 11, p 10, p 01, p 00)(0) (2) Calculate 2|i(1), 1|i(1) and 0|i(1) using Eqs. 1 -3, (3) Calculate (1) using 2|i(1), 1|i(1) and 0|i(1) based on Eqs. 4 -10, (4) Repeat (2) and (3) until convergence.

Example: Human Obesity
3ca3fca17646fefca3fdfcb1d50c078c.ppt