1 Risk and Rates of Return Chapter 6

Interest Rate Interest rate represents the cost of money It is the opportunity cost of money: v. It shows the return lost from not investing in a comparable risk investment. v. It is expected to compensate the investor for the time, inflation, and risk. 4

Conceptually: Interest Rates 5

Conceptually: Nominal risk-free Interest Rate krf Interest Rates 6

Conceptually: Nominal risk-free Interest Rate krf = Interest Rates 7

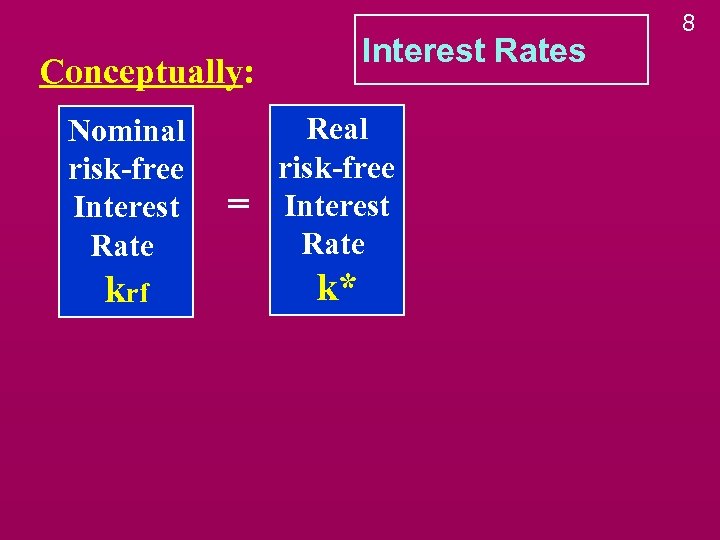Interest Rates Conceptually: Nominal risk-free Interest Rate krf = Real risk-free Interest Rate k* 8

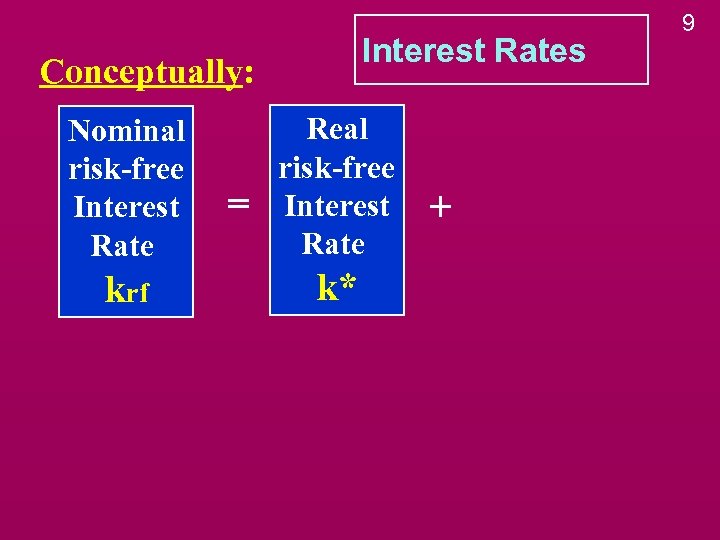Interest Rates Conceptually: Nominal risk-free Interest Rate krf = Real risk-free Interest Rate k* + 9

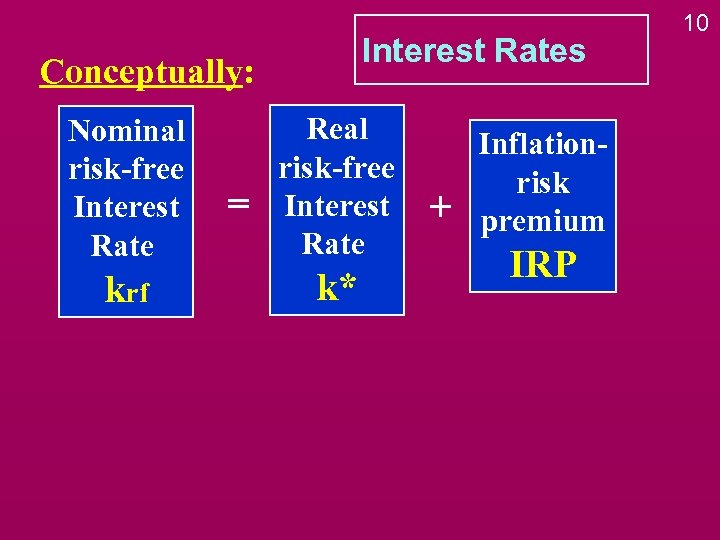Interest Rates Conceptually: Nominal risk-free Interest Rate krf = Real risk-free Interest Rate k* + Inflationrisk premium IRP 10

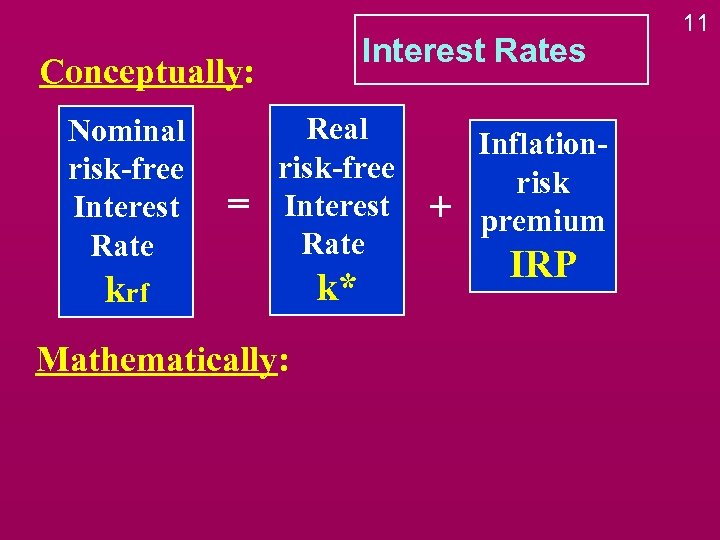Interest Rates Conceptually: Nominal risk-free Interest Rate = Real risk-free Interest Rate krf Mathematically: k* + Inflationrisk premium IRP 11

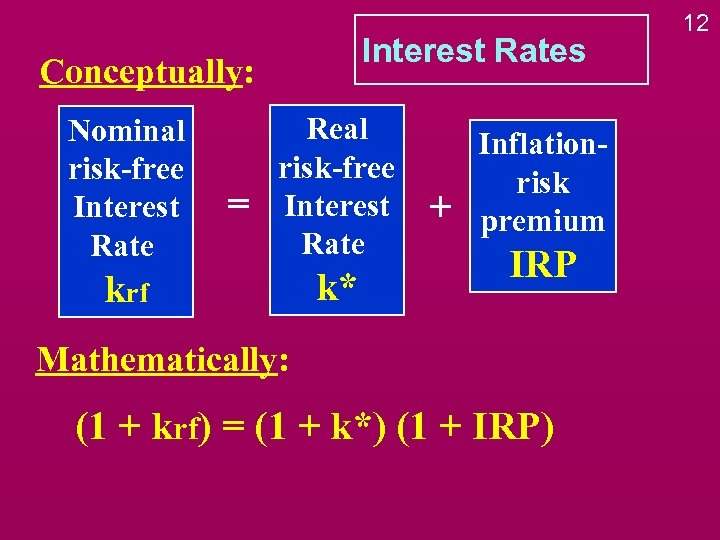Interest Rates Conceptually: Nominal risk-free Interest Rate = Real risk-free Interest Rate krf k* + Inflationrisk premium IRP Mathematically: (1 + krf) = (1 + k*) (1 + IRP) 12

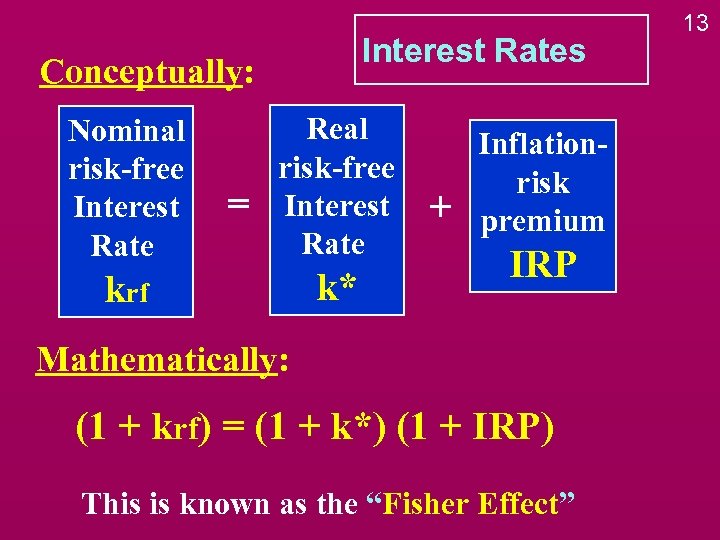Interest Rates Conceptually: Nominal risk-free Interest Rate = Real risk-free Interest Rate krf k* + Inflationrisk premium IRP Mathematically: (1 + krf) = (1 + k*) (1 + IRP) This is known as the “Fisher Effect” 13

Interest Rates 14 Suppose the real rate is 3%, and the nominal rate is 8%. What is the inflation rate premium? (1 + krf) = (1 + k*) (1 + IRP) (1. 08) = (1. 03) (1 + IRP) = (1. 0485), so IRP = 4. 85%

Term Structure of Interest Rates The pattern of rates of return for debt securities that differ only in the length of time to maturity. 15

Term Structure of Interest Rates 16 The pattern of rates of return for debt securities that differ only in the length of time to maturity. yield to maturity time to maturity (years)

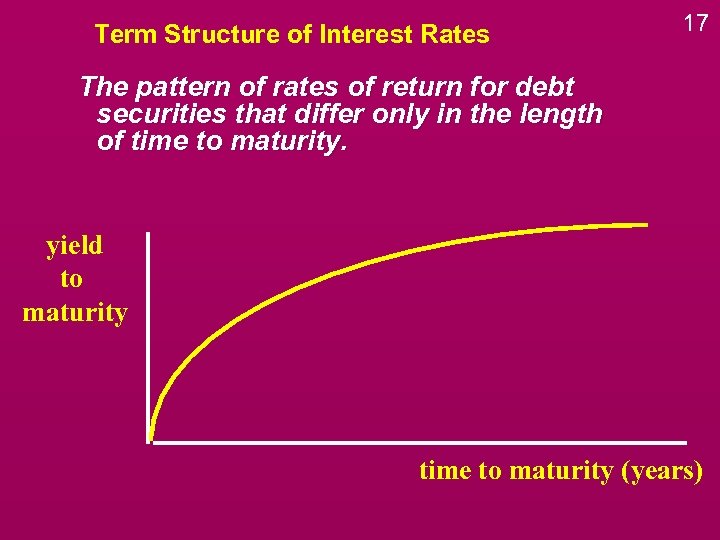Term Structure of Interest Rates 17 The pattern of rates of return for debt securities that differ only in the length of time to maturity. yield to maturity time to maturity (years)

Term Structure of Interest Rates 18 The yield curve may be downward sloping or “inverted” if rates are expected to fall. yield to maturity time to maturity (years)

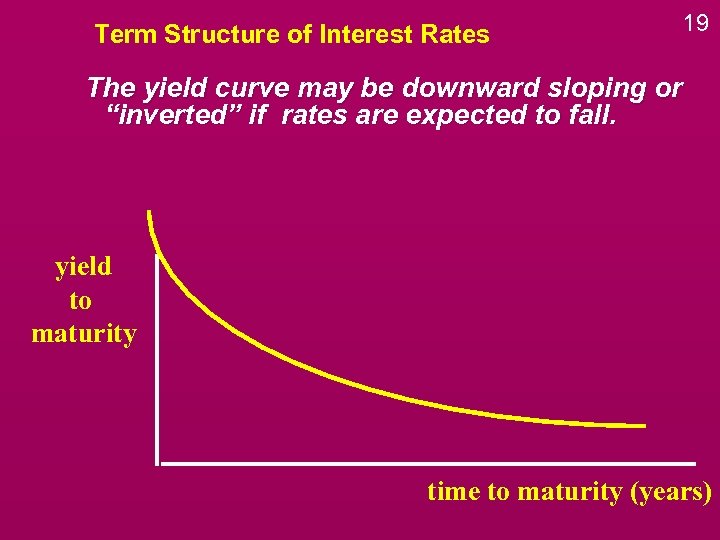Term Structure of Interest Rates 19 The yield curve may be downward sloping or “inverted” if rates are expected to fall. yield to maturity time to maturity (years)

20 For a Treasury security, what is the required rate of return?

21 For a Treasury security, what is the required rate of return? Required rate of return =

22 For a Treasury security, what is the required rate of return? Required rate of return = Risk-free rate of return Since Treasuries are essentially free of default risk, the rate of return on a Treasury security is considered the “risk-free” rate of return.

23 For a corporate stock or bond, what is the required rate of return?

24 For a corporate stock or bond, what is the required rate of return? Required rate of return =

25 For a corporate stock or bond, what is the required rate of return? Required rate of return = Risk-free rate of return

26 For a corporate stock or bond, what is the required rate of return? Required rate of return = Risk-free rate of return + Risk premium How large of a risk premium should we require to buy a corporate security?

Returns Expected Return - the return that an investor expects to earn on an asset, given its price, growth potential, etc. Required Return - the return that an investor requires on an asset given its risk and market interest rates. 27

Risk and Rates of Return Two Components of return Periodic cash flows 28

Risk and Rates of Return Two Components of return Periodic cash flows Price Change (capital gains) 29

Risk and Rates of Return Holding Period return 30

Risk and Rates of Return Holding Period return P t + Dt = ----- - 1 Pt-1 31

Risk and Rates of Return Holding Period return P t + Dt = ----- - 1 Pt-1 (Pt - Pt-1) + Dt = --------Pt-1 32

Risk and Rates of Return Expected Return v. Expected return is based on expected cash flows (not accounting profits) Return can be expressed as Cash Flows or Percentage Return 33

Risk and Rates of Return Expected Return v. Expected return is based on expected cash flows (not accounting profits) v. In an uncertain world future cash flows are not known with certainty 34

Risk and Rates of Return 35 Expected Return v. Expected return is based on expected cash flows (not accounting profits) v. In uncertain world future cash flows are not known with certainty v. To calculate expected return, compute the weighted average of all possible returns

Risk and Rates of Return 36 Expected Return v. Expected return is based on expected cash flows (not accounting profits) v. In uncertain world future cash flows are not known with certainty v. To calculate expected return, compute the weighted average of possible returns v. Calculating Expected Return:

Risk and Rates of Return 37 Expected Return v. Expected return is based on expected cash flows (not accounting profits) v. In uncertain world future cash flows are not known with certainty v. To calculate expected return, compute the weighted average of possible returns v. Calculating Expected Return: where ki = Return state i P(ki) = Probability of ki occurring N = Number of possible states

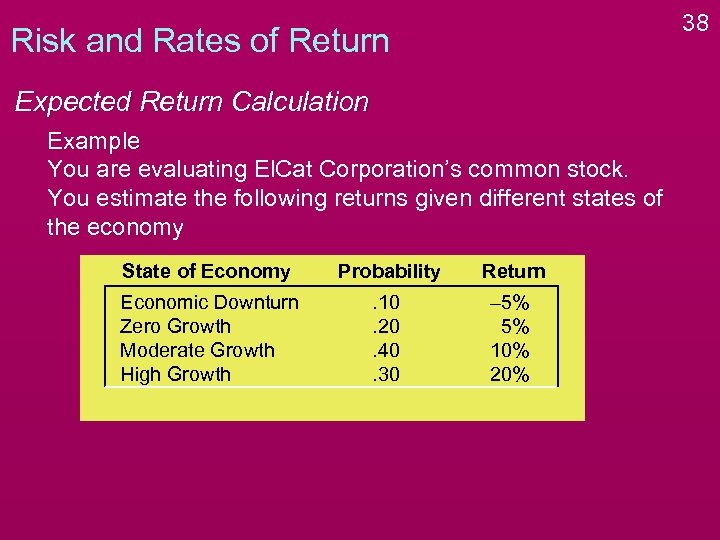38 Risk and Rates of Return Expected Return Calculation Example You are evaluating El. Cat Corporation’s common stock. You estimate the following returns given different states of the economy State of Economy Probability Return Economic Downturn Zero Growth Moderate Growth High Growth . 10. 20. 40. 30 – 5% 5% 10% 20%

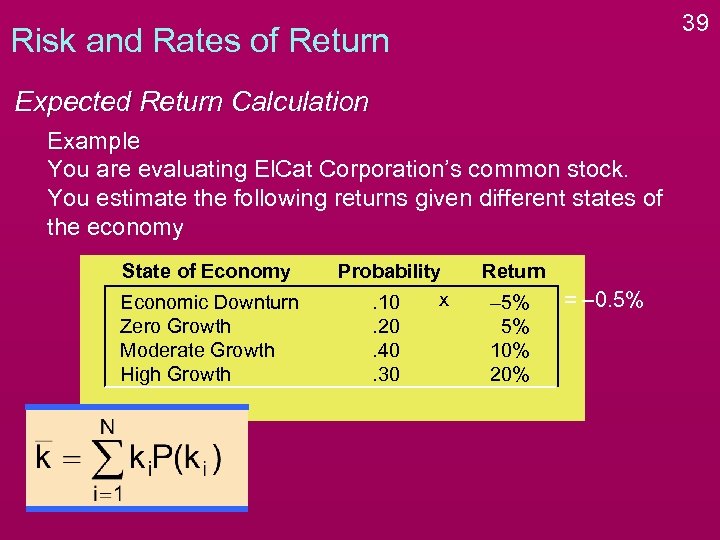39 Risk and Rates of Return Expected Return Calculation Example You are evaluating El. Cat Corporation’s common stock. You estimate the following returns given different states of the economy State of Economy Economic Downturn Zero Growth Moderate Growth High Growth Probability x. 10. 20. 40. 30 Return – 5% 5% 10% 20% = – 0. 5%

40 Risk and Rates of Return Expected Return Calculation Example You are evaluating El. Cat Corporation’s common stock. You estimate the following returns given different states of the economy State of Economy Economic Downturn Zero Growth Moderate Growth High Growth Probability x. 10 x. 20. 40. 30 Return – 5% 5% 10% 20% = – 0. 5% = 1%

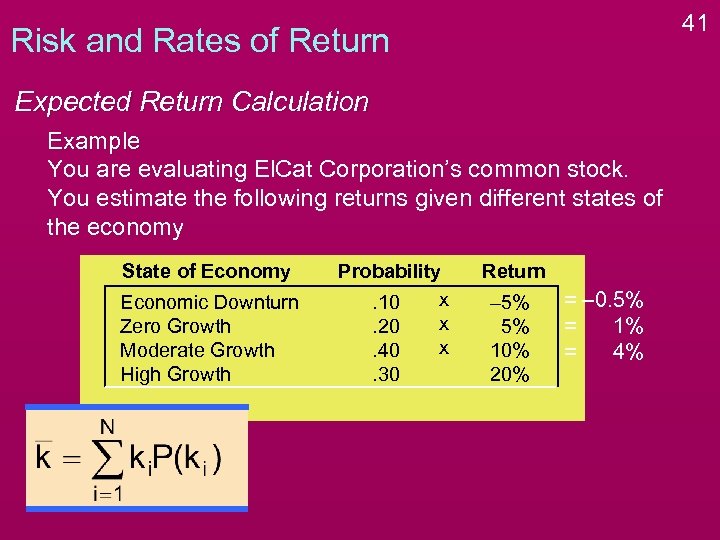41 Risk and Rates of Return Expected Return Calculation Example You are evaluating El. Cat Corporation’s common stock. You estimate the following returns given different states of the economy State of Economy Economic Downturn Zero Growth Moderate Growth High Growth Probability x. 10 x. 20 x. 40. 30 Return – 5% 5% 10% 20% = – 0. 5% = 1% = 4%

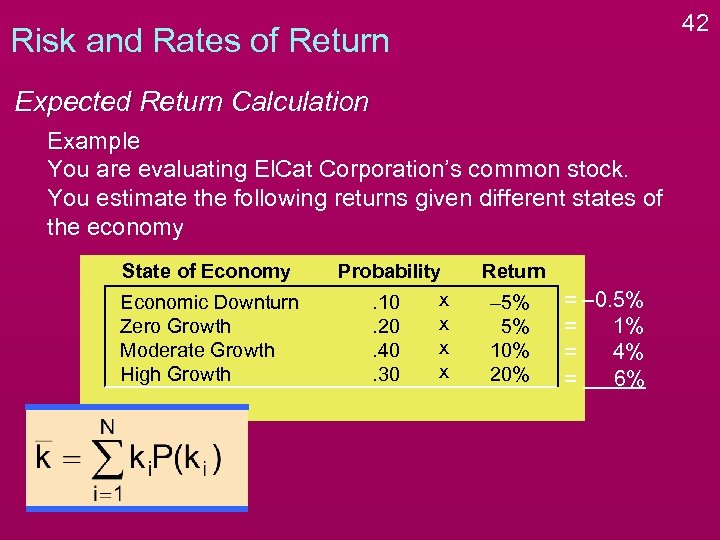42 Risk and Rates of Return Expected Return Calculation Example You are evaluating El. Cat Corporation’s common stock. You estimate the following returns given different states of the economy State of Economy Economic Downturn Zero Growth Moderate Growth High Growth Probability x. 10 x. 20 x. 40 x. 30 Return – 5% 5% 10% 20% = – 0. 5% = 1% = 4% = 6%

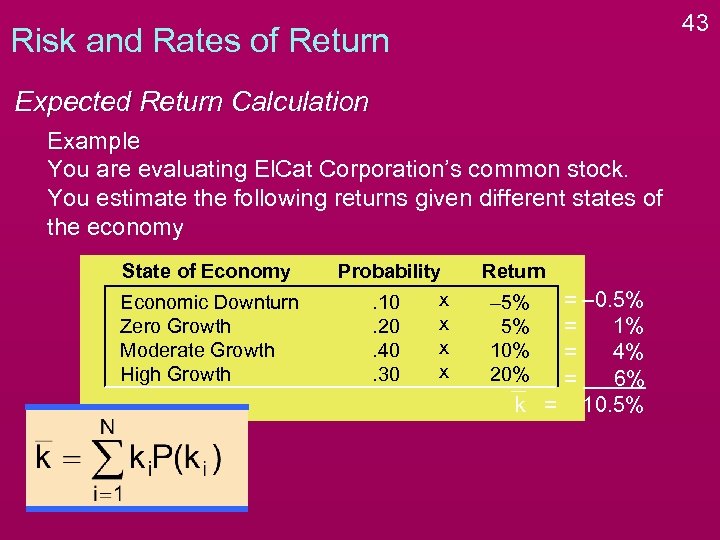43 Risk and Rates of Return Expected Return Calculation Example You are evaluating El. Cat Corporation’s common stock. You estimate the following returns given different states of the economy State of Economy Economic Downturn Zero Growth Moderate Growth High Growth Probability x. 10 x. 20 x. 40 x. 30 Return = – 0. 5% = 1% = 4% = 6% k = 10. 5% – 5% 5% 10% 20%

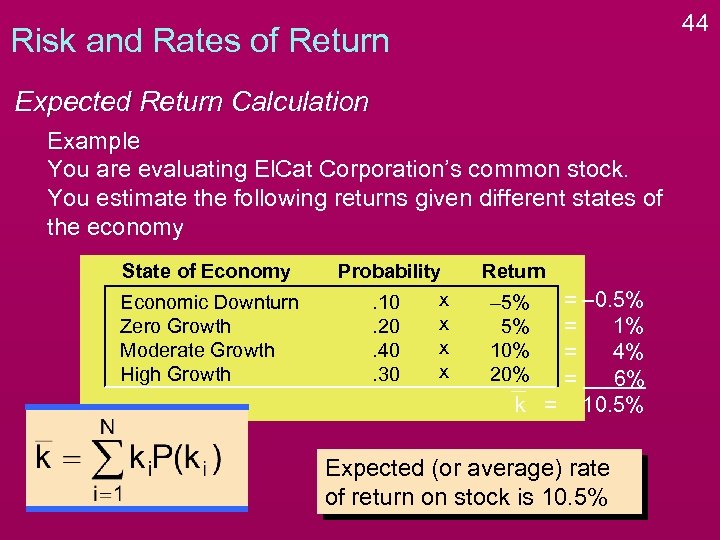44 Risk and Rates of Return Expected Return Calculation Example You are evaluating El. Cat Corporation’s common stock. You estimate the following returns given different states of the economy State of Economy Economic Downturn Zero Growth Moderate Growth High Growth Probability x. 10 x. 20 x. 40 x. 30 Return = – 0. 5% = 1% = 4% = 6% k = 10. 5% – 5% 5% 10% 20% Expected (or average) rate of return on stock is 10. 5%

Risk and Rates of Return Risk v. Risk is the uncertainty of future outcomes 45

Risk and Rates of Return Risk v. Risk is the uncertainty of future outcomes Example You evaluate two investments: El. Cat Corporation’s common stock and a one year Gov't Bond paying 6%. The return on the Gov't Bond does not depend on the state of the economy--you are guaranteed a 6% return. 46

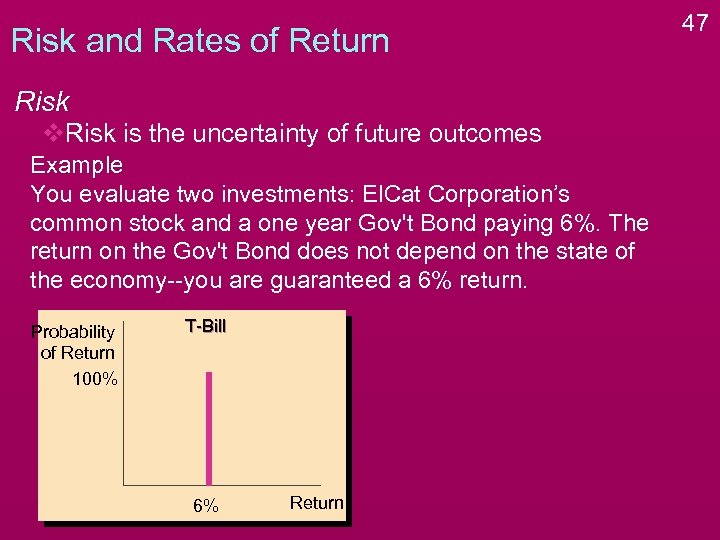Risk and Rates of Return Risk v. Risk is the uncertainty of future outcomes Example You evaluate two investments: El. Cat Corporation’s common stock and a one year Gov't Bond paying 6%. The return on the Gov't Bond does not depend on the state of the economy--you are guaranteed a 6% return. Probability of Return 100% T-Bill 6% Return 47

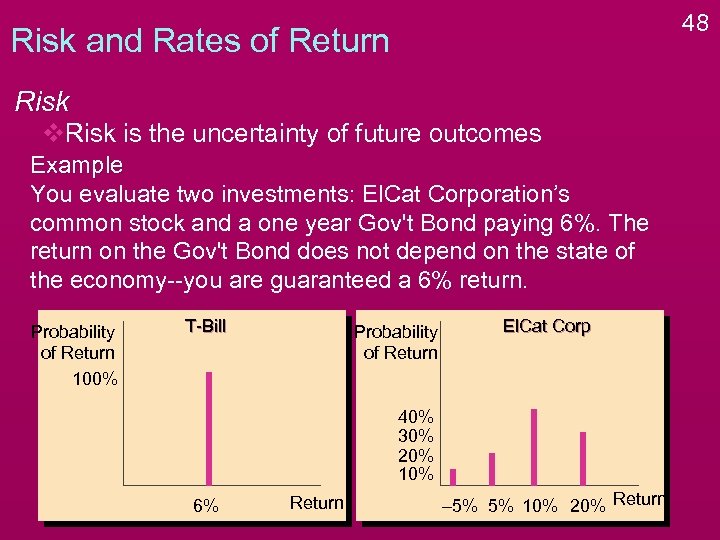48 Risk and Rates of Return Risk v. Risk is the uncertainty of future outcomes Example You evaluate two investments: El. Cat Corporation’s common stock and a one year Gov't Bond paying 6%. The return on the Gov't Bond does not depend on the state of the economy--you are guaranteed a 6% return. Probability of Return 100% T-Bill Probability of Return El. Cat Corp 40% 30% 20% 10% 6% Return – 5% 5% 10% 20% Return

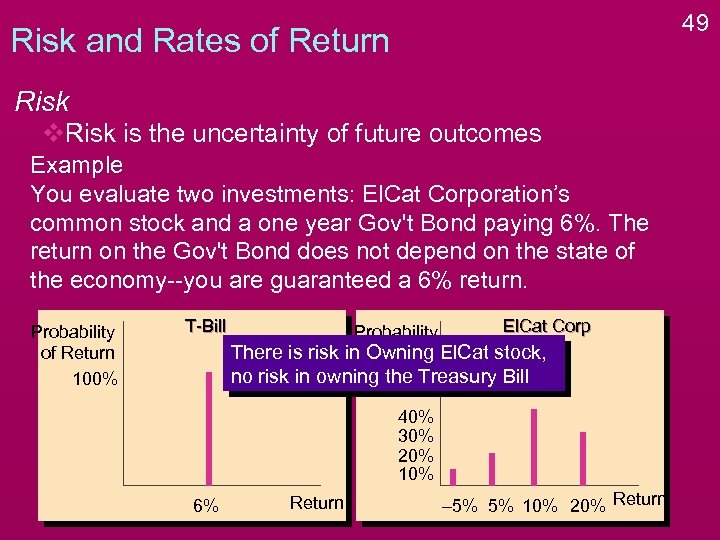49 Risk and Rates of Return Risk v. Risk is the uncertainty of future outcomes Example You evaluate two investments: El. Cat Corporation’s common stock and a one year Gov't Bond paying 6%. The return on the Gov't Bond does not depend on the state of the economy--you are guaranteed a 6% return. Probability of Return 100% T-Bill El. Cat Corp Probability There is risk in of Return El. Cat stock, Owning no risk in owning the Treasury Bill 40% 30% 20% 10% 6% Return – 5% 5% 10% 20% Return

Risk and Rates of Return Measuring Risk v. Standard Deviation (s) measure the dispersion of returns. 50

Risk and Rates of Return Measuring Risk v. Standard Deviation (s) measure the dispersion of returns. 51

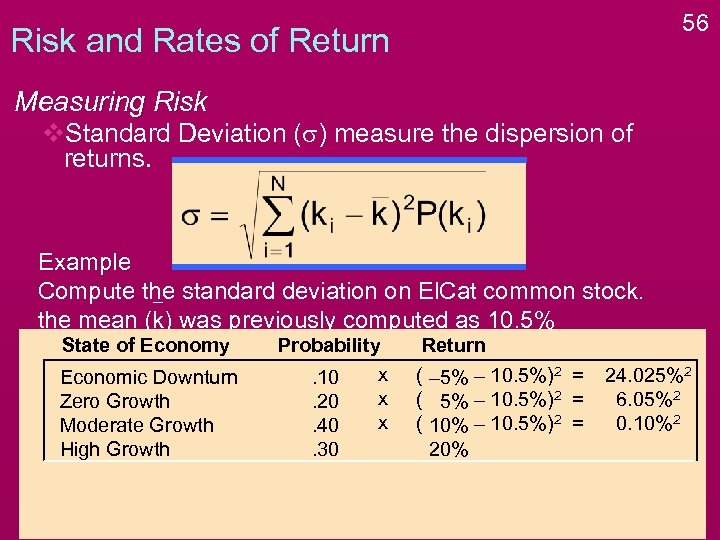
Risk and Rates of Return Measuring Risk v. Standard Deviation (s) measure the dispersion of returns. Example Compute the standard deviation on El. Cat common stock. the mean (k) was previously computed as 10. 5% 52

53 Risk and Rates of Return Measuring Risk v. Standard Deviation (s) measure the dispersion of returns. Example Compute the standard deviation on El. Cat common stock. the mean (k) was previously computed as 10. 5% State of Economy Probability Return Economic Downturn Zero Growth Moderate Growth High Growth . 10. 20. 40. 30 – 5% 5% 10% 20%

54 Risk and Rates of Return Measuring Risk v. Standard Deviation (s) measure the dispersion of returns. Example Compute the standard deviation on El. Cat common stock. the mean (k) was previously computed as 10. 5% State of Economy Economic Downturn Zero Growth Moderate Growth High Growth Probability x. 10. 20. 40. 30 Return ( – 5% – 10. 5%)2 = 5% 10% 24. 025%2

55 Risk and Rates of Return Measuring Risk v. Standard Deviation (s) measure the dispersion of returns. Example Compute the standard deviation on El. Cat common stock. the mean (k) was previously computed as 10. 5% State of Economy Economic Downturn Zero Growth Moderate Growth High Growth Probability x. 10 x. 20. 40. 30 Return ( – 5% – 10. 5%)2 = ( 5% – 10. 5%)2 = 10% 24. 025%2 6. 05%2

56 Risk and Rates of Return Measuring Risk v. Standard Deviation (s) measure the dispersion of returns. Example Compute the standard deviation on El. Cat common stock. the mean (k) was previously computed as 10. 5% State of Economy Economic Downturn Zero Growth Moderate Growth High Growth Probability x. 10 x. 20 x. 40. 30 Return ( – 5% – 10. 5%)2 = ( 10% – 10. 5%)2 = 20% 24. 025%2 6. 05%2 0. 10%2

57 Risk and Rates of Return Measuring Risk v. Standard Deviation (s) measure the dispersion of returns. Example Compute the standard deviation on El. Cat common stock. the mean (k) was previously computed as 10. 5% State of Economy Economic Downturn Zero Growth Moderate Growth High Growth Probability x. 10 x. 20 x. 40 x. 30 Return ( ( – 5% – 10. 5%)2 = 24. 025%2– -6. 05%2 5% 10. 5%)2 = 0. 10%2 10% – 10. 5%)2 = 27. 075%2

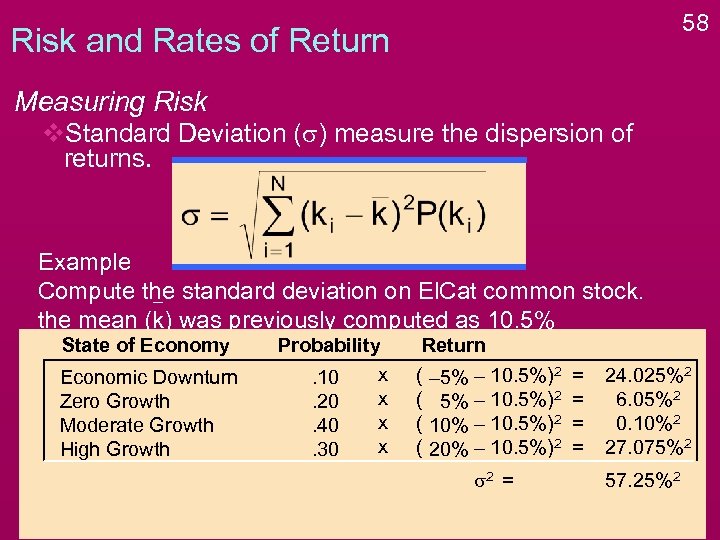58 Risk and Rates of Return Measuring Risk v. Standard Deviation (s) measure the dispersion of returns. Example Compute the standard deviation on El. Cat common stock. the mean (k) was previously computed as 10. 5% State of Economy Economic Downturn Zero Growth Moderate Growth High Growth Probability x. 10 x. 20 x. 40 x. 30 Return ( ( – 5% – 10. 5%)2 10% – 10. 5%)2 20% – 10. 5%)2 s 2 = = = 24. 025%2 6. 05%2 0. 10%2 27. 075%2 57. 25%2

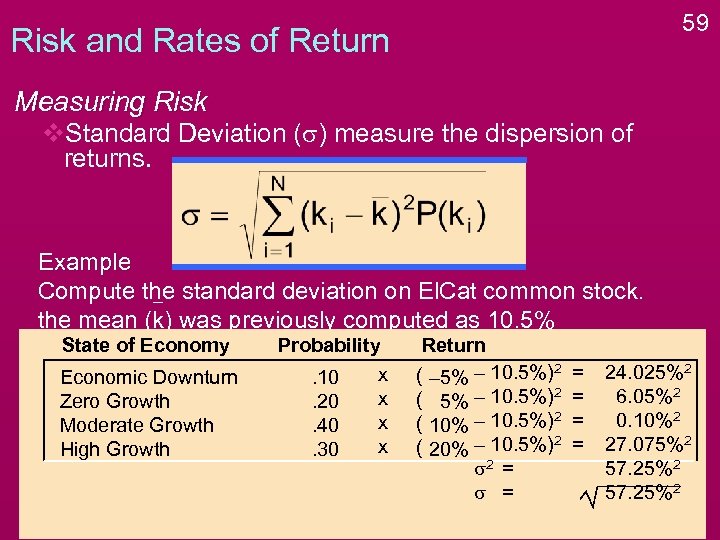59 Risk and Rates of Return Measuring Risk v. Standard Deviation (s) measure the dispersion of returns. Example Compute the standard deviation on El. Cat common stock. the mean (k) was previously computed as 10. 5% State of Economy Economic Downturn Zero Growth Moderate Growth High Growth Probability x. 10 x. 20 x. 40 x. 30 Return ( – 5% – 10. 5%)2 ( 10% – 10. 5%)2 ( 20% – 10. 5%)2 s 2 = s = = = 24. 025%2 6. 05%2 0. 10%2 27. 075%2 57. 25%2

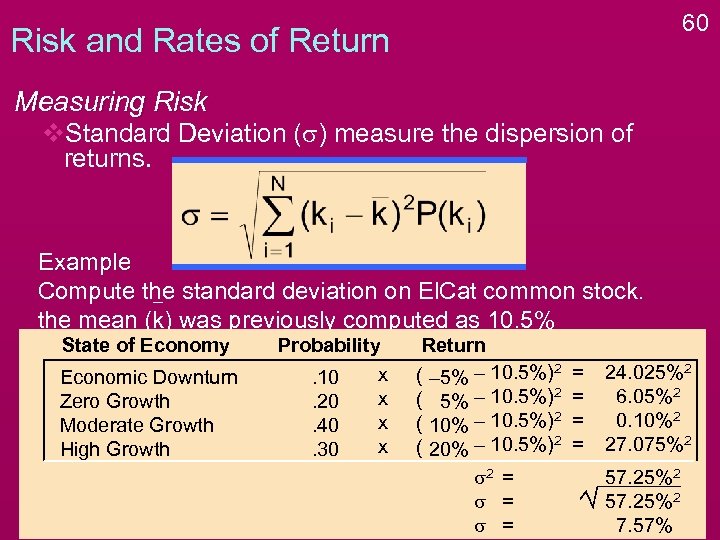60 Risk and Rates of Return Measuring Risk v. Standard Deviation (s) measure the dispersion of returns. Example Compute the standard deviation on El. Cat common stock. the mean (k) was previously computed as 10. 5% State of Economy Economic Downturn Zero Growth Moderate Growth High Growth Probability x. 10 x. 20 x. 40 x. 30 Return ( – 5% – 10. 5%)2 ( 10% – 10. 5%)2 ( 20% – 10. 5%)2 s 2 = s = = = 24. 025%2 6. 05%2 0. 10%2 27. 075%2 57. 25%2 7. 57%

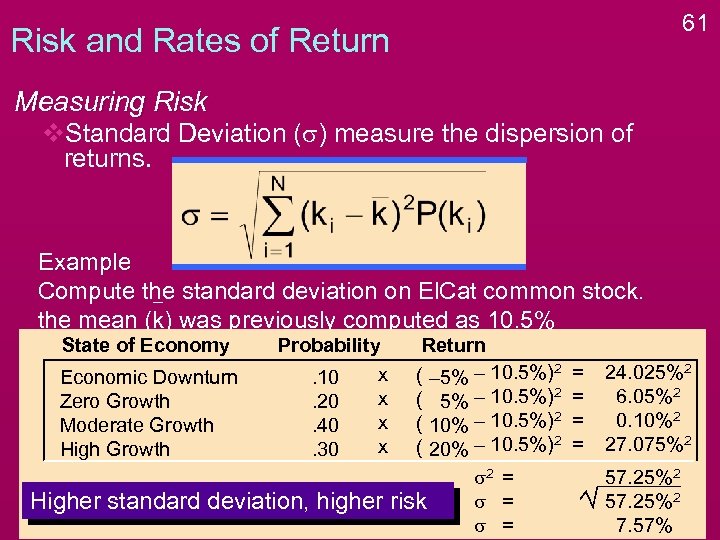61 Risk and Rates of Return Measuring Risk v. Standard Deviation (s) measure the dispersion of returns. Example Compute the standard deviation on El. Cat common stock. the mean (k) was previously computed as 10. 5% State of Economy Economic Downturn Zero Growth Moderate Growth High Growth Probability x. 10 x. 20 x. 40 x. 30 Higher standard deviation, higher Return ( – 5% – 10. 5%)2 ( 10% – 10. 5%)2 ( 20% – 10. 5%)2 s 2 = s = risk s = = = 24. 025%2 6. 05%2 0. 10%2 27. 075%2 57. 25%2 7. 57%

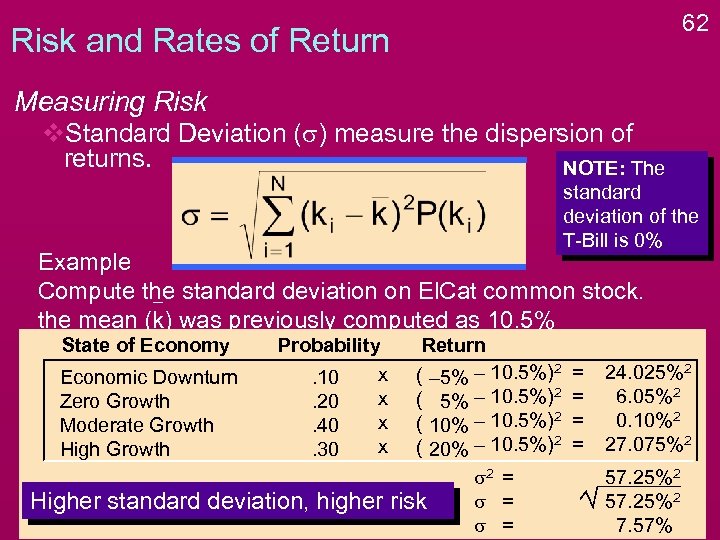62 Risk and Rates of Return Measuring Risk v. Standard Deviation (s) measure the dispersion of returns. NOTE: The standard deviation of the T-Bill is 0% Example Compute the standard deviation on El. Cat common stock. the mean (k) was previously computed as 10. 5% State of Economy Economic Downturn Zero Growth Moderate Growth High Growth Probability x. 10 x. 20 x. 40 x. 30 Higher standard deviation, higher Return ( – 5% – 10. 5%)2 ( 10% – 10. 5%)2 ( 20% – 10. 5%)2 s 2 = s = risk s = = = 24. 025%2 6. 05%2 0. 10%2 27. 075%2 57. 25%2 7. 57%

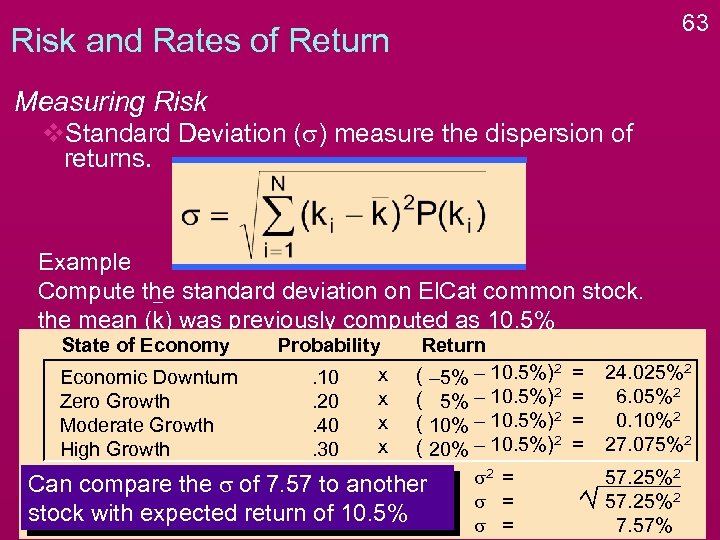63 Risk and Rates of Return Measuring Risk v. Standard Deviation (s) measure the dispersion of returns. Example Compute the standard deviation on El. Cat common stock. the mean (k) was previously computed as 10. 5% State of Economy Probability x. 10 x. 20 x. 40 x. 30 Return ( – 5% – 10. 5%)2 Economic Downturn ( 5% – 10. 5%)2 Zero Growth ( 10% – 10. 5%)2 Moderate Growth ( 20% – 10. 5%)2 High Growth s 2 = Can compare the s of 7. 57 to another s = stock with expected return of 10. 5% s = = = 24. 025%2 6. 05%2 0. 10%2 27. 075%2 57. 25%2 7. 57%

Risk and Rates of Return 64 Measuring Risk Standard Deviation (s) for historical data can be used to measure the dispersion of historical returns.

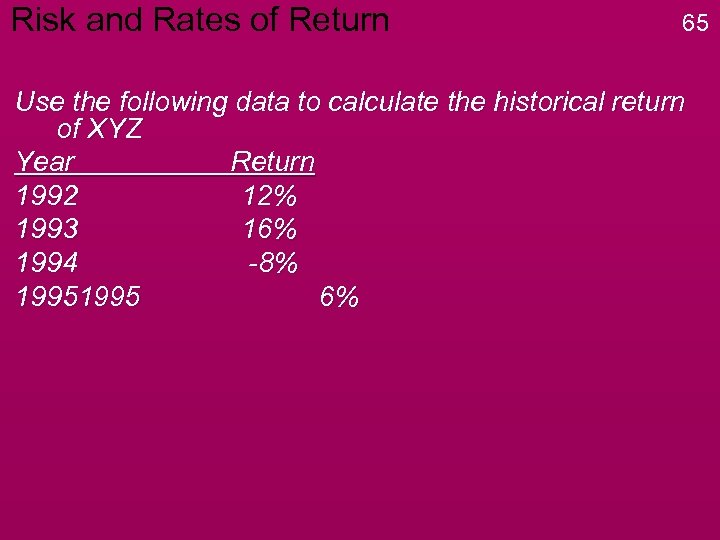Risk and Rates of Return 65 Use the following data to calculate the historical return of XYZ Year Return 1992 12% 1993 16% 1994 -8% 1995 6%

Risk and Rates of Return Risk and Diversification v. Risk of a company's stock can be separated into two parts: 66

Risk and Rates of Return Risk and Diversification v. Risk of a company's stock can be separated into two parts: v. Firm Specific Risk - Risk due to factors within the firm 67

Risk and Rates of Return Risk and Diversification v. Risk of a company's stock can be separated into two parts: v. Firm Specific Risk - Risk due to factors within the firm Stock price will most likely fall if a major government contract is discontinued unexpectedly. 68

Risk and Rates of Return Risk and Diversification v. Risk of a company's stock can be separated into two parts: v. Firm Specific Risk - Risk due to factors within the firm v. Market related Risk - Risk due to overall market conditions 69

Risk and Rates of Return Risk and Diversification v. Risk of a company's stock can be separated into two parts: v. Firm Specific Risk - Risk due to factors within the firm v. Market related Risk - Risk due to overall market conditions Stock price is likely to rise if overall stock market is doing well. 70

Risk and Rates of Return Risk and Diversification v. Risk of a company's stock can be separated into two parts: v. Firm Specific Risk - Risk due to factors within the firm v. Market related Risk - Risk due to overall market conditions v. Diversification: If investors hold stock of many companies, the firm specific risk will be canceled out: Investors diversify portfolio. 71

Risk and Rates of Return Risk and Diversification v. Risk of a company's stock can be separated into two parts: v. Firm Specific Risk - Risk due to factors within the firm v. Market related Risk - Risk due to overall market conditions v. Diversification: If investors hold stock of many companies, the firm specific risk will be canceled out: Investors diversify portfolio. Firm specific risk also called diversifiable risk or unsystematic risk 72

Risk and Rates of Return 73 Risk and Diversification v. Risk of a company's stock can be separated into two parts: v. Firm Specific Risk - Risk due to factors within the firm v. Market related Risk - Risk due to overall market conditions v. Diversification: If investors hold stock of many companies, the firm specific risk will be canceled out: Investors diversify portfolio. v. Even if hold many stocks, cannot eliminate the market related risk

Risk and Rates of Return 74 Risk and Diversification v. Risk of a company's stock can be separated into two parts: v. Firm Specific Risk - Risk due to factors within the firm v. Market related Risk - Risk due to overall market conditions v. Diversification: If investors hold stock of many companies, the firm specific risk will be canceled out: Investors diversify portfolio. v. Even if hold many stocks, cannot eliminate the market related risk Market related risk is also called non-diversifiable risk or systematic risk

Risk and Rates of Return Risk and Diversification v. If an investor holds enough stocks in portfolio (about 20) company specific (diversifiable) risk is virtually eliminated 75

Risk and Rates of Return Risk and Diversification v. If an investor holds enough stocks in portfolio (about 20) company specific (diversifiable) risk is virtually eliminated Variability of Returns Market Related Risk Number of stocks in Portfolio 76

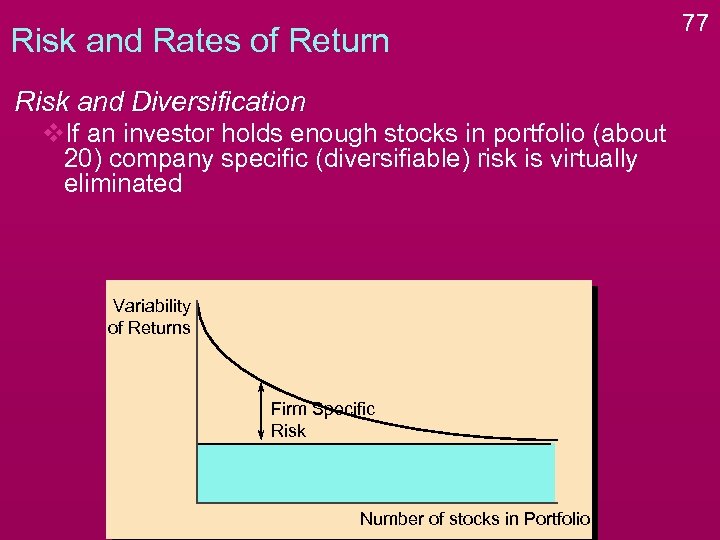Risk and Rates of Return Risk and Diversification v. If an investor holds enough stocks in portfolio (about 20) company specific (diversifiable) risk is virtually eliminated Variability of Returns Firm Specific Risk Number of stocks in Portfolio 77

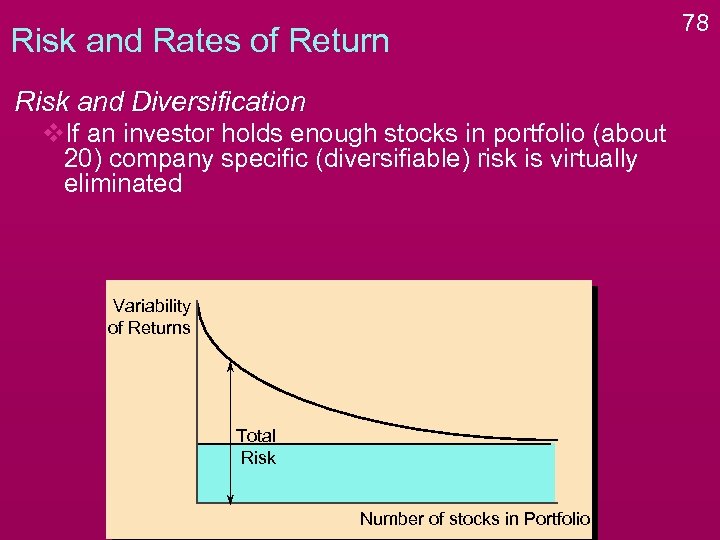Risk and Rates of Return Risk and Diversification v. If an investor holds enough stocks in portfolio (about 20) company specific (diversifiable) risk is virtually eliminated Variability of Returns Total Risk Number of stocks in Portfolio 78

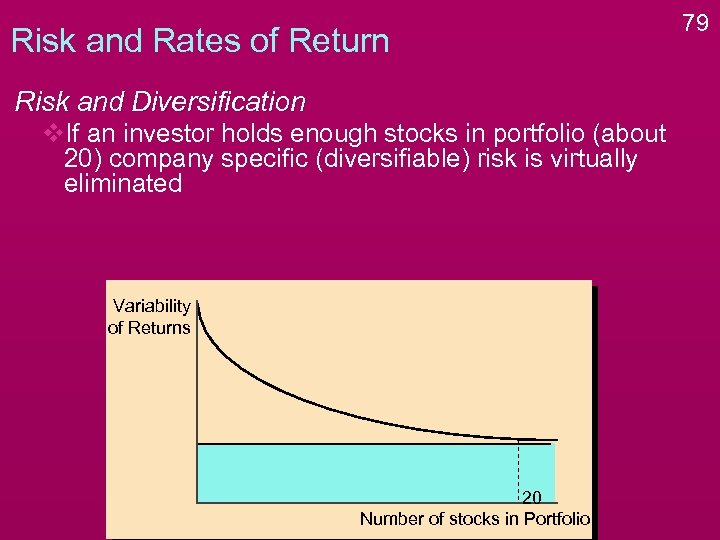Risk and Rates of Return Risk and Diversification v. If an investor holds enough stocks in portfolio (about 20) company specific (diversifiable) risk is virtually eliminated Variability of Returns 20 Number of stocks in Portfolio 79

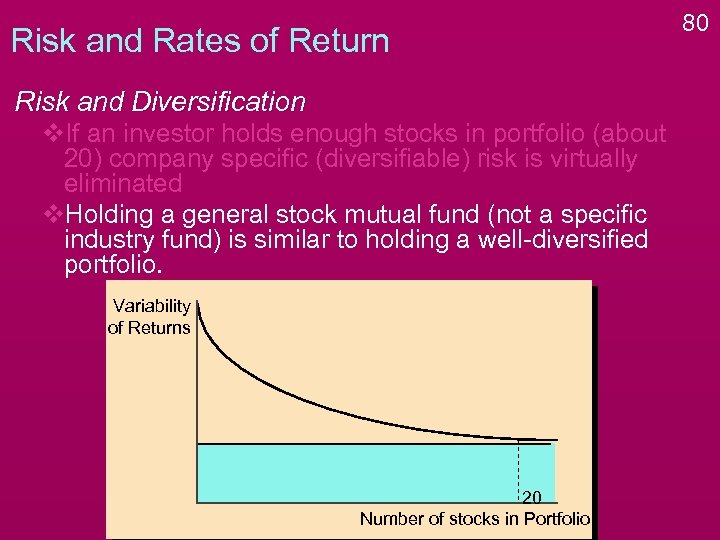Risk and Rates of Return Risk and Diversification v. If an investor holds enough stocks in portfolio (about 20) company specific (diversifiable) risk is virtually eliminated v. Holding a general stock mutual fund (not a specific industry fund) is similar to holding a well-diversified portfolio. Variability of Returns 20 Number of stocks in Portfolio 80

Risk and Rates of Return 81 Measuring Market Risk v. Market risk is the risk of the overall market. To measure the market risk we need to compare individual stock returns to the overall market returns.

Risk and Rates of Return 82 Measuring Market Risk v. Market risk is the risk of the overall market. To measure the market risk we need to compare individual stock returns to the overall market returns. v. A proxy for the market is usually used: An index of stocks such as the S&P 500

Risk and Rates of Return 83 Measuring Market Risk v. Market risk is the risk of the overall market, so to measure need to compare individual stock returns to the overall market returns. v. A proxy for the market is usually used: An index of stocks such as the S&P 500 v. Market risk measures how individual stock returns are affected by this market

Risk and Rates of Return 84 Measuring Market Risk v. Market risk is the risk of the overall market, so to measure need to compare individual stock returns to the overall market returns. v. A proxy for the market is usually used: An index of stocks such as the S&P 500 v. Market risk measures how individual stock returns are affected by this market v. Regress individual stock returns on Market index

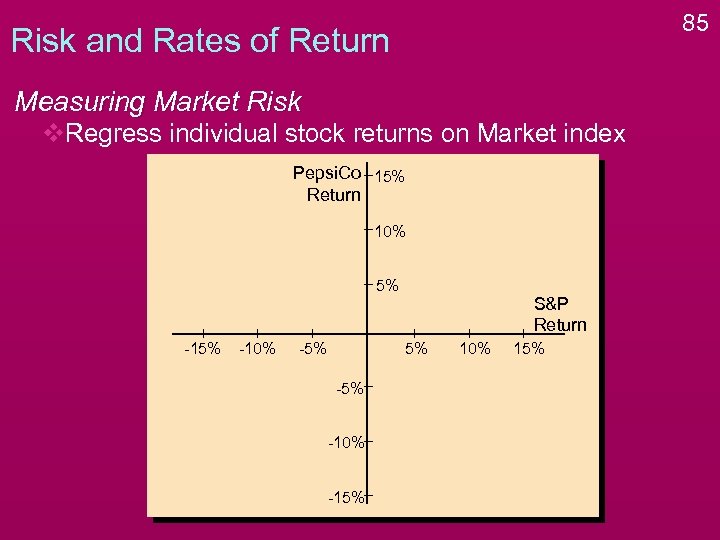85 Risk and Rates of Return Measuring Market Risk v. Regress individual stock returns on Market index Pepsi. Co 15% Return 10% 5% -10% -5% S&P Return 5% -10% -15% 10% 15%

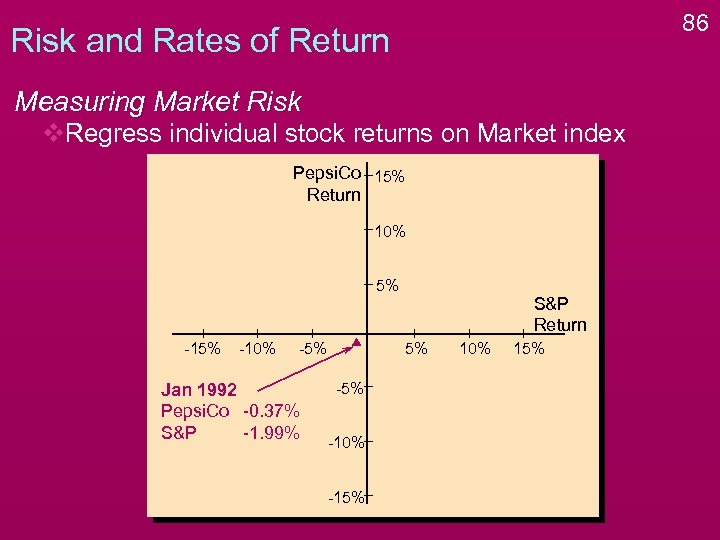86 Risk and Rates of Return Measuring Market Risk v. Regress individual stock returns on Market index Pepsi. Co 15% Return 10% 5% -10% -5% Jan 1992 Pepsi. Co -0. 37% S&P -1. 99% S&P Return 5% -10% -15% 10% 15%

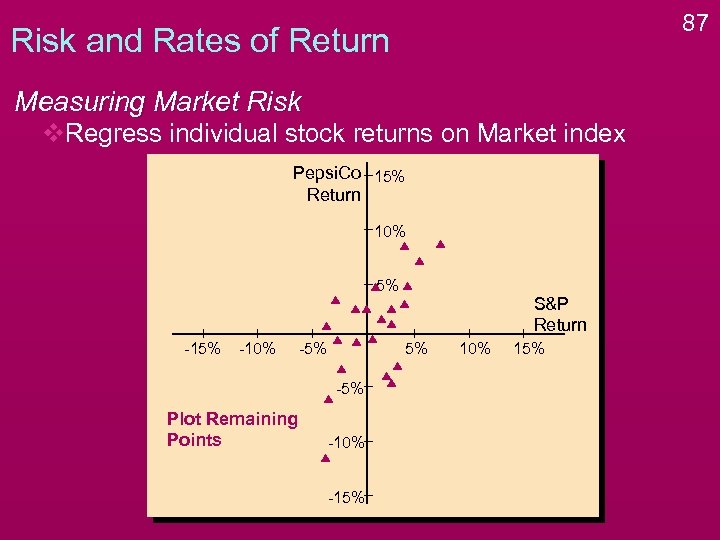87 Risk and Rates of Return Measuring Market Risk v. Regress individual stock returns on Market index Pepsi. Co 15% Return 10% 5% -10% -5% 5% -5% Plot Remaining Points S&P Return -10% -15% 10% 15%

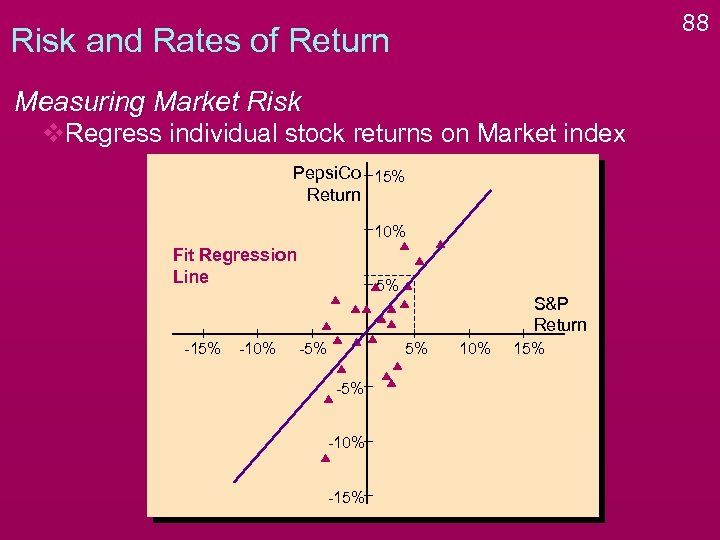88 Risk and Rates of Return Measuring Market Risk v. Regress individual stock returns on Market index Pepsi. Co 15% Return 10% Fit Regression Line -15% -10% 5% -5% S&P Return 5% -10% -15% 10% 15%

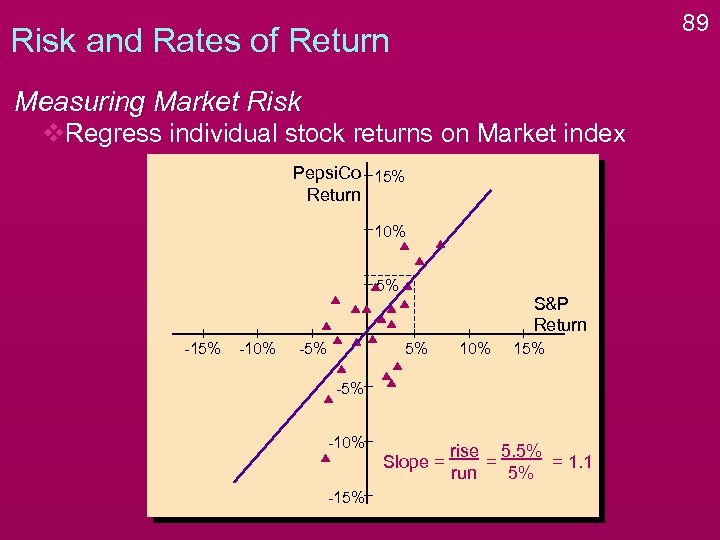89 Risk and Rates of Return Measuring Market Risk v. Regress individual stock returns on Market index Pepsi. Co 15% Return 10% 5% -10% -5% S&P Return 5% 10% 15% -10% Slope = -15% rise 5. 5% = = 1. 1 run 5%

Risk and Rates of Return Measuring Market Risk v. Market Risk is measured by Beta 90

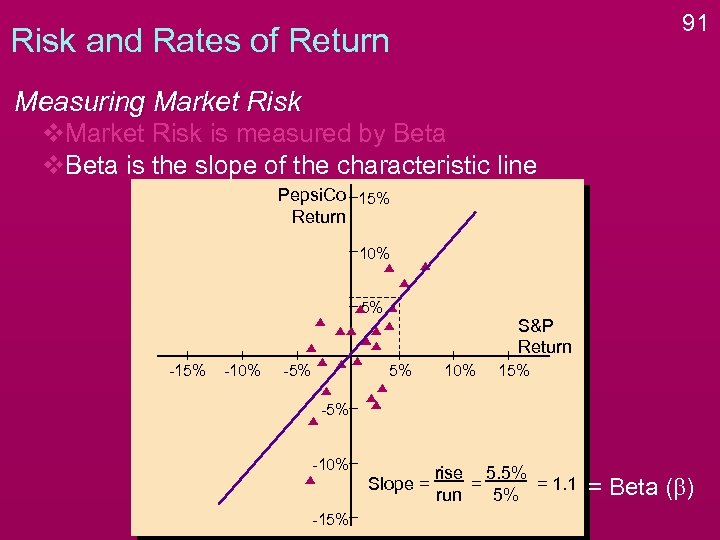91 Risk and Rates of Return Measuring Market Risk v. Market Risk is measured by Beta v. Beta is the slope of the characteristic line Pepsi. Co 15% Return 10% 5% -10% -5% S&P Return 5% 10% 15% -10% Slope = -15% rise 5. 5% = = 1. 1 run 5% = Beta (b)

Risk and Rates of Return Measuring Market Risk v. Market Risk is measured by Beta v. Beta is the slope of the characteristic line v. Interpreting Beta v. Beta = 1 Market Beta = 1 Company with a beta of 1 has average risk 92

Risk and Rates of Return Measuring Market Risk v. Market Risk is measured by Beta v. Beta is the slope of the characteristic line v. Interpreting Beta v. Beta = 1 Market Beta = 1 Company with a beta of 1 has average risk v. Beta < 1 Low Risk Company Return on stock will be less affected by the market than average 93

Risk and Rates of Return Measuring Market Risk v. Market Risk is measured by Beta v. Beta is the slope of the characteristic line v. Interpreting Beta v. Beta = 1 Market Beta = 1 Company with a beta of 1 has average risk v. Beta < 1 Low Risk Company Return on stock will be less affected by the market than average v. Beta > 1 High Market Risk Company Stock return will be more affected by the market than average 94

Risk and Rates of Return Required Minimum rate of return necessary to Rate of = attract investors to buy funds Return 95

Risk and Rates of Return Required Minimum rate of return necessary to Rate of = attract investors to buy funds Return u. Required rate of return, K, depends on the risk-free rate(Krf) and the risk premium(Krp) 96

Risk and Rates of Return 97 Required Minimum rate of return necessary to Rate of = attract investors to buy funds Return u. Required rate of return, K, depends on the risk-free rate(Krf) and the risk premium(Krp) u. Using the capital asset pricing model (CAPM) the risk premium(Krp) depends on market risk

Risk and Rates of Return 98 Required Minimum rate of return necessary to Rate of = attract investors to buy funds Return u. Required rate of return, K, depends on the risk-free rate(Krf) and the risk premium(Krp) u. Using the capital asset pricing model (CAPM) the risk premium(Krp) depends on market risk Security Market Line Kj = Krf + bj ( Km – Krf ) where: Kj = required rate of return on the jth security Bj = Beta for the jth security

Risk and Rates of Return Security Market Line Kj = Krf + bj ( Km – Krf ) Example: If the expected return on the market is 12% and the risk free rate is 5%: 99

Risk and Rates of Return Security Market Line Kj = Krf + bj ( Km – Krf ) Example: If the expected return on the market is 12% and the risk free rate is 5%: Kj = 5% + bj (12% – 5% ) 100

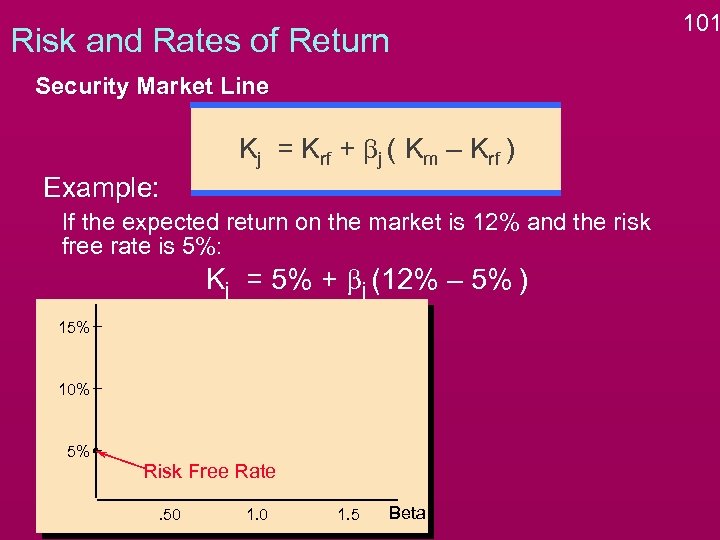Risk and Rates of Return Security Market Line Kj = Krf + bj ( Km – Krf ) Example: If the expected return on the market is 12% and the risk free rate is 5%: Kj = 5% + bj (12% – 5% ) 15% 10% 5% Risk Free Rate. 50 1. 5 Beta 101

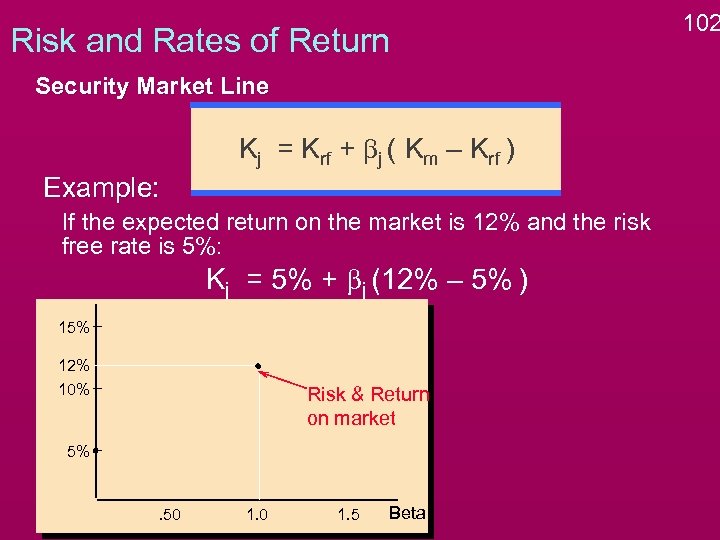Risk and Rates of Return Security Market Line Kj = Krf + bj ( Km – Krf ) Example: If the expected return on the market is 12% and the risk free rate is 5%: Kj = 5% + bj (12% – 5% ) 15% 12% 10% Risk & Return on market 5% . 50 1. 5 Beta 102

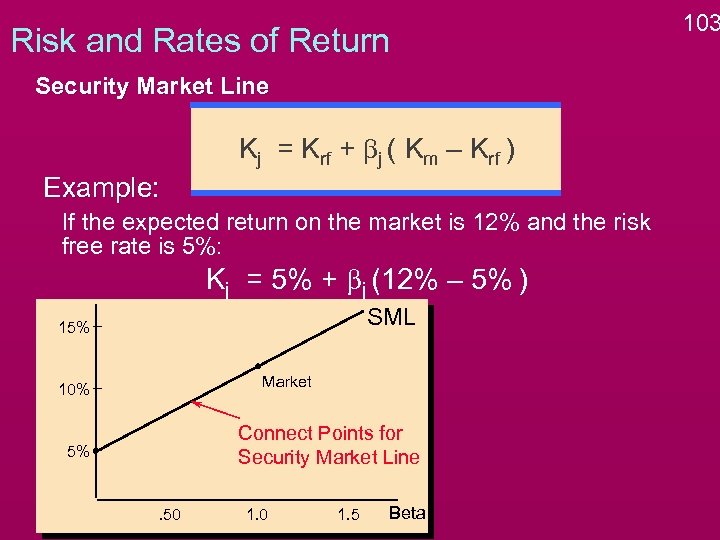Risk and Rates of Return Security Market Line Kj = Krf + bj ( Km – Krf ) Example: If the expected return on the market is 12% and the risk free rate is 5%: Kj = 5% + bj (12% – 5% ) SML 15% Market 10% Connect Points for Security Market Line 5% . 50 1. 5 Beta 103

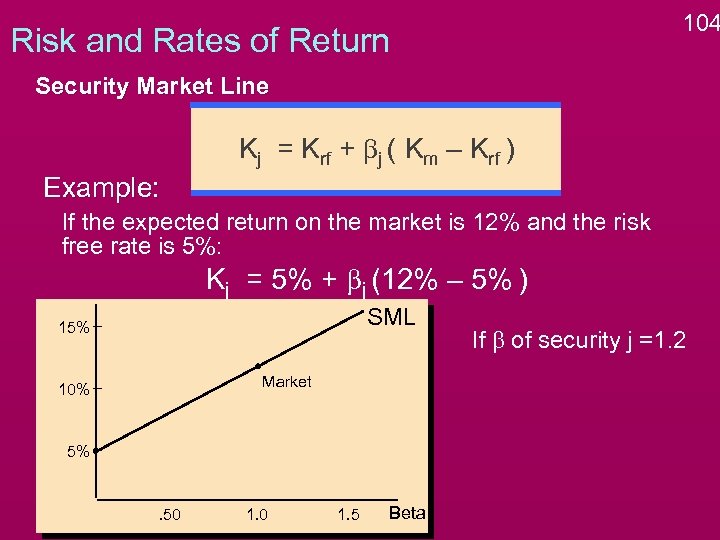104 Risk and Rates of Return Security Market Line Kj = Krf + bj ( Km – Krf ) Example: If the expected return on the market is 12% and the risk free rate is 5%: Kj = 5% + bj (12% – 5% ) SML 15% Market 10% 5% . 50 1. 5 Beta If b of security j =1. 2

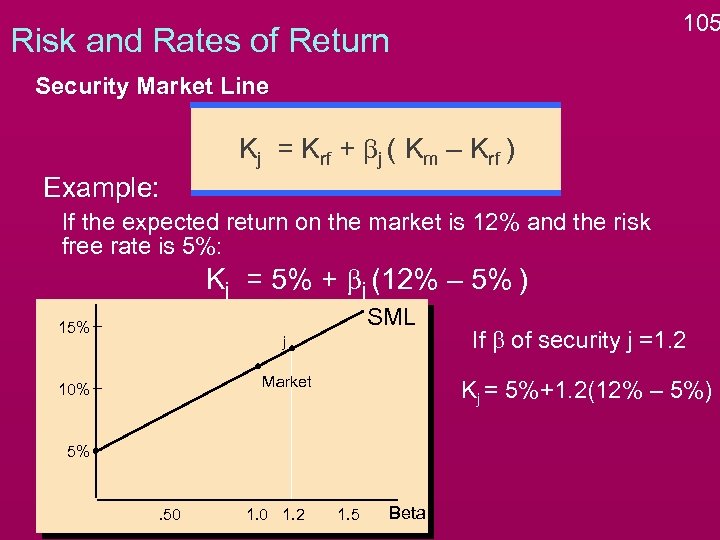105 Risk and Rates of Return Security Market Line Kj = Krf + bj ( Km – Krf ) Example: If the expected return on the market is 12% and the risk free rate is 5%: Kj = 5% + bj (12% – 5% ) SML 15% j Market 10% Kj = 5%+1. 2(12% – 5%) 5% . 50 1. 2 If b of security j =1. 2 1. 5 Beta

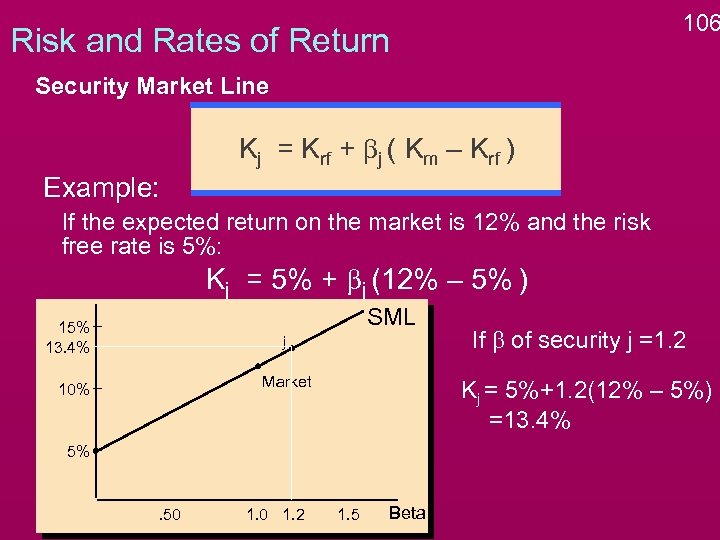106 Risk and Rates of Return Security Market Line Kj = Krf + bj ( Km – Krf ) Example: If the expected return on the market is 12% and the risk free rate is 5%: Kj = 5% + bj (12% – 5% ) SML 15% 13. 4% j Market 10% Kj = 5%+1. 2(12% – 5%) =13. 4% 5% . 50 1. 2 If b of security j =1. 2 1. 5 Beta

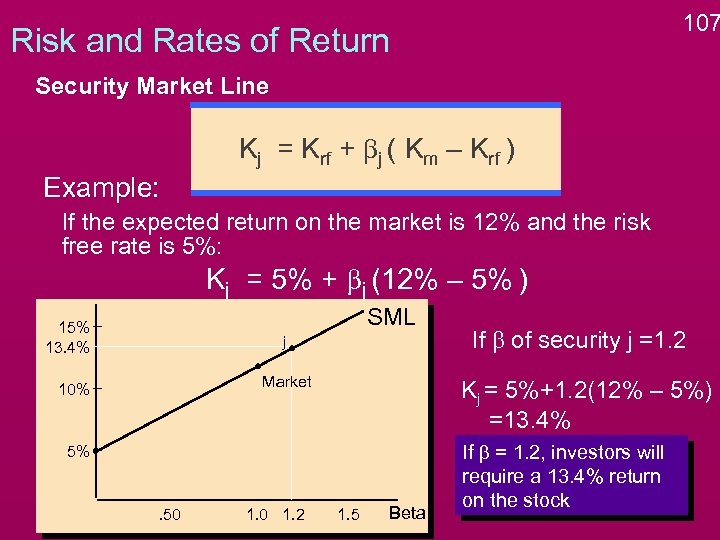107 Risk and Rates of Return Security Market Line Kj = Krf + bj ( Km – Krf ) Example: If the expected return on the market is 12% and the risk free rate is 5%: Kj = 5% + bj (12% – 5% ) SML 15% 13. 4% j Market 10% Kj = 5%+1. 2(12% – 5%) =13. 4% 5% . 50 1. 2 If b of security j =1. 2 1. 5 Beta If b = 1. 2, investors will require a 13. 4% return on the stock

Risk and Rates of Return 108 ki : Expected (or required) rate of return from an investment i. KRF : Risk free rate of return (e. g. , 3 moth T-Bill rate) k. M : Expected return from a market (e. g. , S&P 500) portfolio (k. M - k. RF) : Market Risk Premium b(k. M - k. RF) : Risk Premium on asset i

Risk and Rates of Return Portfolio Return = S wi x ki Return of a portfolio is the weighted average return of individual securities in the portfolio. Portfolio beta = S wi x bi Beta of a portfolio is the weighted average beta of individual securities in the portfolio. 109